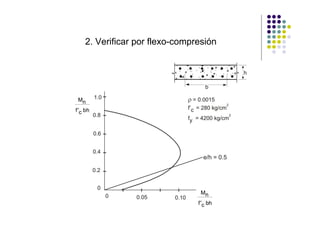
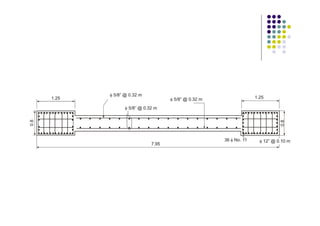
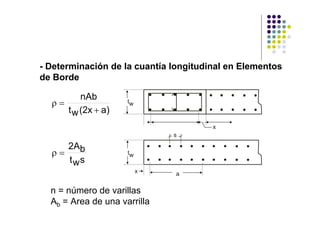
Este documento describe los requisitos de diseño para muros estructurales de concreto armado según el código ACI. Incluye: 1) refuerzo mínimo requerido en muros, 2) métodos para análisis de compresión y flexo-compresión, 3) fuerzas cortantes generadas por cargas paralelas, 4) requisitos sísmicos, y 5) un ejemplo de diseño de muro estructural.

1. Ing. Roberto Morales Morales
MUROS
ESTRUCTURALES
Diseño en Concreto Armado 2006 ICG

2. 19.1 Muros Estructurales de concreto
armado
a) Refuerzo Mínimo en Muros
El código define un refuerzo mínimo para controlar el
agrietamiento de la estructura.
b) Refuerzo Mínimo Vertical
- Para varillas menores o igual que No.5.
fy>4200 kg/cm2
Av mín = 0.0012 bh
- Para cualquier otro tipo de varilla
AV mín = 0.0015 bh

3. - Para mallas electrosoldadas, de alambre liso o
corrugado no mayor que W31 y D31
Av mín = 0.0012 bh
c) Refuerzo Mínimo Horizontal
- Para varillas menores o igual que No.5.
fy>4200kg/cm2
Ah mín = 0.0020 bh
- Para cualquier otro tipo de varilla
Ah mín = 0.0025 bh

4. - Para mallas electrosoldadas, de alambre liso o
corrugado no mayor que W31 y D31
Ah mín = 0.0020 bh
Distancia entre juntas Refuerzo mínimo
7-9m 0.0025 bh
9 - 12 m 0.0030 bh
12 - 15 m 0.0035 bh
15 - 20 m 0.0040 bh

6. Consideraciones:
- Espaciamiento del refuerzo horizontal y vertical no
será mayor que tres veces el espesor del muro ni
mayor que 45 cm.
- El acero vertical no necesita estribos laterales si la
cuantía verticales < 0.01 o si este refuerzo no trabaja a
compresión.
- Si h>25 cm Refuerzo horizontal y vertical debe
distribuirse en dos capas.

7. d) Cargas concentradas en Muros
Si una carga concentrada es aplicada, se considera
que ésta es resistida sólo por una porción del muro:

8. Se debe verificar que las cargas concentradas no
ocasionen el aplastamiento del concreto debajo de
ellas.
Pu A2
≤ 0.85 f'c A1 ≤ 1.7f'c A1
φ A1

10. 19.2 Compresión y flexo-compresión en
muros de Concreto Armado
19.2.1 Método Empírico
Se emplea si satisface las siguientes condiciones:
1. La sección del muro es rectangular y la excentricidad
de la carga axial es menor que un sexto de la
dimensión del muro, es decir el muro está sometido
integramente a compresión.
2. El espesor del muro es:
menor dimension del muro y h ≥ 10cm
h≥
25

11. Para muros de sótano el espesor mínimo es 20 cm.
Se estima la resistencia a la compresión del muro a
través de la siguiente fórmula:
⎛ 2⎞
⎛ kL c ⎞ ⎟
φPnw = 0.55 φf'c A g ⎜ 1 − ⎜ ⎟ ⎟
⎜ ⎝ 32h ⎠
⎝ ⎠
φ = 0.70 (La solicitación es de flexocompresión)
Lc = Altura libre del muro.
Ag = Area de la sección transversal del muro
k = factor de altura efectiva

12. Tipo de Muro Condiciones de Apoyo k
Muro apoyado Si uno de los apoyos 0.8
arriba y abajo tiene el giro restringido
Si ambos apoyos tiene 1.0
el giro restringido
Muro con apoyos Si ambos apoyos tienen 2.0
que admite desplazamiento relativo
desplazamiento
relativo

13. 19.2.2 Método General de Diseño
Si la carga axial se ubica fuera del tercio central, parte de
su sección central estará sometido a tracción y por la
tanto, se diseñará siguiendo los criterios para columnas
sometido a flexocompresión. Será necesario tomar en
cuenta el efecto de la esbeltez para el análisis y por lo
tanto se emplea el método de amplificación de momentos
siempre que:
kL
< 100
r

14. Según este método, el parámetro EL deberá tomarse
según las siguientes expresiones:
EcΙ g ⎛ e⎞
EL = ⎜ 0.5 − ⎟
b ⎝ h⎠
Ec = Modulo de elasticidad del concreto
Ι g = Momento de Inercia de la seccion bruta
β = 0.9 + 0.5 β 2 - 12ρ
d

15. EcΙ g
EL ≥ 0.1
b
PDu
bd : Para pórticos arriostrados, βd =
Pu
EcΙ g
EL ≤ 0.4
β
VDu
bd : Para pórticos no arriostrados, βd =
Vu

16. ρ = cuantía de acero vertical respecto al área bruta de
concreto.
e = Excentricidad de la carga axial.
h = Espesor del muro.
19.2.3 Fuerzas cortantes generadas por cargas
Paralelas a la cara del muro
a) Resistencia del concreto al corte
Se tomará el menor valor de:
N d
Vc = 0.88 f'c hd + u
4L w

17. ⎡ ⎛ Nu ⎞ ⎤
⎢ L w ⎜ 0.33 f'c + 0.2 ⎟ ⎥
⎢ 0.16 f' + ⎝ L wh ⎠ ⎥ hd
Vc = ⎢ c ⎥
Mu L w
⎢ − ⎥
⎢ Vu 2 ⎥
⎣ ⎦
(Unidades en kg y cm)
Nu : Carga axial amplificada en el muro, positiva si es
de compresión y negativa si es de tracción.
Mu : Momento flector amplificado en la sección
analizada.
Vu : Fuerza cortante amplificada en la sección
analizada.
d : Peralte efectivo del muro, se estima como d = 0.8 Lw
Lw : Longitud del muro.

18. El código ACI recomienda que la resistencia del
concreto al corte entre el apoyo y la sección ubicada al
valor menor entre Lw /2 , hw/2 deberá considerarse
para el cálculo en dicha sección.
En lugar de estas fórmulas se puede usar las siguientes
que resultan ser más prácticas.
- Si el muro está en compresión:
Vc = 0.53 f'c hd
- Si el muro está en tracción.
⎛ 0.029 Nu ⎞
Vc = 0.53 ⎜ 1 +
⎜
⎟ f'c hd
⎝ Ag ⎟ ⎠

19. Resistencia nominal máxima del muro
Vn ≤ 2.7 f'c hd
Consideraciones:
φVc
Si: Vu ≤
2
se considerará el refuerzo mínimo considerado
anteriormente.
Si: φVc
< Vu ≤ φVc
2

20. la cuantía mínima del refuerzo horizontal será 0.0025 y
el espaciamiento del acero será menor que:
Lw
, 3h, 45 cm
5
b) Diseño Por Corte
Si Vu > φ Vc , el área de acero horizontal se determinará
de la siguiente forma:
(Vu − φVc )s2
A vh =
φfyd

21. Siendo Avh el área del refuerzo horizontal en una franja
del muro de ancho s2. La cuantía del refuerzo vertical,
ρv , respecto a una sección bruta horizontal, deberá
cumplir:
⎛
ρ ≥ 0.0025 + 0.5⎜ 2.5 −
v ⎝
hw ⎞
(
⎟ ρ − 0.0025
Lw ⎠ h
)
ó 0.0025, pero no necesita ser mayor que el requerido
por refuerzo horizontal, su espaciamiento no excederá
Lw
, 3h, 45 cm
3

22. c) Diseño por Flexo-compresión
Teniéndose la distribución del acero vertical, se
elabora el diagrama de interacción del muro con la
cual verificamos que nuestros valores Mu/φ y Pu/φ se
encuentren dentro de la zona del diagrama de
interacción. En caso contrario será necesario hacer
uso de diagramas hechos para una distribución dada
de acero y calcular nuestra área de acero necesaria.

24. 19.3 Requisitos del codigo ACI para
resistencia sismica de muros
estructurales
Consideraciones de diseño de muros dúctiles (ACI
318-05)
- Muros Esbeltos:
hw
≥2
Lw
- Comportamiento similar a una viga en voladizo.
- Momentos grandes en la base del muro: Formación de
rótulas plásticas
- En una longitud apreciable (0.5 dw a 1.0 dw).

25. - Fuerzas cortantes significativas: Fisuramiento por
tracción diagonal.
h mín = 1.5Lw Longitud probable de rótulas plásticas
Vu = V base
- Muros Cortos:
hw
<2
Lw

26. - Cargas verticales relativamente pequeñas.
- Requerimientos menores por flexión (momentos de
volteo).
-La fuerza cortante significativa: Fisuramiento por
tracción diagonal.
- Refuerzos en Muros Estructurales
ρn ≥ 0.0025
ρv ≥ 0.0025
Si Vu ≥ 0.53 f' c Acv , entonces se pondrán 2 capas de
refuerzo o más.
Para muros bajos: hw / Lw ≤ 2 ⇒ ρv ≥ ρh

27. - Espaciamientos Máximos
- Horizontal: 45 cm
- Vertical: 45 cm
- Resistencia al Cortante de Muros Estructurales
Vn = A cv (α f'c + ρ fy )
n
Para valores de hw / Lw
hw
α c = 0.80 para ≤ 1.5 entre 1.5 y 2.0, se
Lw
interpolará linealmente los
hw valores de αc.
α c = 0.53 para ≥ 2.0
Lw

28. - Elementos de Borde o de Confinamiento en Muros
Estructurales
a) Los muros continuos desde la cimentación hasta el
extremo superior que tienen una sección crítica por
flexión y carga axial, la zona de compresión será
reforzada con elementos de borde especiales:
Lw
c≥
600 (δ u / h w )
donde: δ u / h w ≥ 0.007
c = profundidad del eje neutro.
δ = desplazamiento de diseño.

29. Verticalmente el refuerzo deberá extenderse una distancia:
Lw Mu
≥ ;≥
2 4Vu
b) Se pondrán elementos de confinamiento especiales,
donde el esfuerzo de compresión máxima que ocurre
en la fibra extrema es mayor que 0.20 f'c.
Se puede discontinuar estos elementos si el esfuerzo
de compresión es menor de 0.15 f'c.
Estos esfuerzos se determinaran mediante un análisis
lineal elástico, usando las propiedades de la sección.

30. - Deberá confinarse hasta una distancia no menor
que el mayor valor de: c - 0.1 Lw ó c/2.
- En los bordes con alas está deberá extenderse de la
fibra superior en compresión por lo menos 30 cm.

31. El refuerzo transversal de los elementos de borde deberá
satisfacer los requerimientos para columnas especiales;
este deberá extenderse por lo menos 30 cm en la base.
- Donde no se requiera elementos de borde deberá
satisfacerse lo siguiente:
28.2
a) Si ρ>
fy ,se colocará refuerzo transversal especificado
para columnas, a un espaciamiento no mayor de 20 cm.
b) Si Vu < 0.27A cv f' c ,el refuerzo horizontal deberá
terminar en ganchos de 90° o se colocará un estribo en U.

32. - Determinación de la cuantía longitudinal en Elementos
de Borde
nAb
ρ=
t w (2x + a)
2Ab
ρ=
tws
n = número de varillas
Ab = Area de una varrilla

33. 19.4 Aplicación de diseño de un muro
estructural
Diseñar el muro estructural que debe ser capaz de resistir
en el primer nivel la siguiente combinación de fuerzas de
diseño:
PD = 1280 t Vu = 406 t
PL = 195 t hw = 45 m
Lw = 7.95 m
MB = Momento en la base debido al sismo = 4778 t-m
f'c = 280 kg/cm2
fy = 4200 kg/cm2

34. Del análisis y diseño estructural de las columnas
considerando la dirección transversal se obtiene
dimensiones de 1.25m * 0.80m y refuerzo longitudinal
de 30 φ No.11.

35. - Verificación de necesidad de elementos de
confinamiento
Debe disponerse necesariamente de elementos de
confinamiento si el esfuerzo máximo de compresión en la
fibra extrema es mayor de 0.2 f'c.
Ag = 795*50 + (125*30) *2 = 47250 cm2
⎧ 80 * 125 3
⎪ ⎫
⎪ 545 3
Ι=⎨ + 80 * 125(335)2 ⎬ * 2 + 50 *
⎪ 12 ⎪ 12
⎩ ⎭
4
= 2,945'0.35,937.5cm

36. Lw
pu Mu * 2 2065 * 10 3 6689.2 * 10 5 * 795 / 2
f'c = + = +
Ag Lg 47250 2945'035,937.5
2
= 133.99 kg / cm
f´c = 133.9 kg/cm2 > 0.2 f'c = 0.2 * 280 = 56 kg/cm2
∴ necesita elementos de confinamiento.

37. - Determinación de los refuerzos del muro y columna
de confinamiento
a) Muro
1. Determinación de los requerimientos de refuerzo
mínimo longitudinal y transversal en el muro:
a. Verificar si se requiere refuerzo en dos capas.
Se necesita refuerzo en dos capas si:
- la fuerza cortante factorada en el muro excede
Vu > 0.53 f'c A cv ó

38. - si: h ≥ 25cm
Vu = 406 t > 0.53 f' Acv
c
= 0.53 280 (10)0.5)7.95)=352.53 t
h = 50cm > 25cm
∴ necesita refuerzo en dos capas.
b. Refuerzo longitudinal y transversal requerido en el
muro. Requerimiento mínimo de cuantía.
A sv
ρv = = ρn ≥ 0.0025
A cv

39. Espaciamiento Máximo = 45 cm ó 3h (el menor)
Acv/m = (100)(50)= 5000 cm2/m
El área de acero en cada dirección por cada metro de muro
ρxAcv = 0.0025 * 5000 = 12.5 cm2/m
Usando φ 5/8" ⇒ As= 2*1.98 = 3.96 cm2
As 3.96 cm 2
"s" requerido = = = 0.32m < 0.45
A s/m 12.5 cm 2 /m

40. CONFORME
Considerar φ 5/8" @ 0.32 en 2 capas para el Ref. vertical.
2. Determinar requerimiento de refuerzo por cortante
Vn = A cv (α c f'c + ρ f )
n y
hw
αc = 0.80 para ≤ 1.5
Lw
hw
αc = 0.53 para ≥ 2.0
Lw

41. hw 45 m
Se tiene = = 5.66 > 2∴αc = 0.53
L w 7.95 m
Acv = 50 * 795 = 39750 cm2
Vc = 0.53 f' Acv=0.53 280 (10)(0.50*7.95) = 352.53 t
c
406
V s = Vn - V c = - 352.53 = 324.14 t
0.6 *

42. El valor de φ para el cortante es de 0.85. Sin embargo
deberá usarse φ = 0.6 si la resistencia al cortante
nominal Vn es menor que el cortante correspondiente al
desarrollo de la resistencia a flexión nominal. En forma
conservadora se tomará φ = 0.6.
A v * fy * d 3.96 * 4.2 * 636
S= = = 32.63 cm
Vs 324.14
pero:
s=32.63 ≤ 45 cm
s=32.63 ≤ 3h =150 cm
s=32.63 ≤ 32 cm (cuantía mínima)

43. Usar s = 32 cm
φ 5/8" en 2 capas: Av = 2 * 1.98 = 3.96 cm2
d = 0.8 Lw = 0.8 * 795 = 636 cm
Usar φ 5/8" en dos capas @ 0.32m. para el
Ref.Horizontal

44. b) Columna de confinamiento
1. Verificar si los elementos de confinamiento actuando
como columna corta toman las cargas verticales debido
a cargas de gravedad y de sismo.
Fuerza axial máxima sobre el elemento de
confinamiento:
Pu(muro) Mu
Pumax = +
2 L'w

45. - Pu(muro) = 1.4 (PD + PL + PE)
Pu(muro) = 1.4 (1280 +195 + 0) = 2065 t
- Momento factorado en la base Mu = 1.4 MBASE
Mu = 1.4 * 4778 = 6689 t-m
2065 6689.2
Pumax = + = 2030.89 t
2 6.70

46. Sobre el elemento de confinamiento:
Pu = 2030.89 t
b * h = 80 * 125 cm2
Ast = 30 φ No.11 = 30 * 9.58 = 287.4 cm2
A st
Ρt b*h = = 0.029 > ρmin = 0.01
< ρmáx = 0.06
Pn máx = 0.80 (0.85 f'c (Ag - Ast) + Ast * fy)

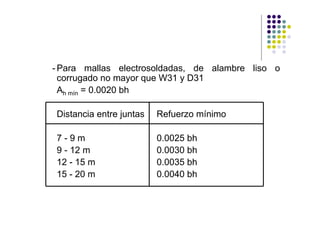
47. Columnas estribadas
Pu máx = φ Pn máx = 0.70 Pn máx
Pu máx = 0.7(0.80) [0.85*280(80*125-287.4)+287.4*4.2]
= 1970.46 t
Pu máx < Pu ∴ NO ES CONFORME
Usar 34 φ No.11Ast = 34 *9.58 = 325.72cm2
Pu máx = 0.70 * 0.8[0.85*0.28 (80*125-325.72) +
325.72 * 4.2]
Pu máx = 2055.48t > Pu = 2030.89t ∴ CONFORME

48. 2. Verificar por flexo-compresión

49. 3. Determinar los requerimientos de refuerzo
transversal por confinamiento
s ≤ tmenor 80
= = 20 cm
4 4
s, en la dirección de la longitud menor
⎧ ⎛ Ag ⎞ f'c
⎪ 0.3s hc ⎜ − 1⎟
⎪ ⎝ A ch ⎠ fy
A sh ≥ ⎨
⎪ 0.09s h f'c
⎪ c f
⎩ y

50. Considerando estribos de φ 1/2" @ 0.10 cm
hc = 125 - (2 * 4 + 1.27) = 115.73 cm
⎧ ⎛ 80 * 125 ⎞ 280
⎪ 0.3 * 10 * 115.73⎜ − 1⎟ = 4.33 cm2
⎝ 8424 ⎠ 4200
⎪
A sh ≥ ⎨
⎪ 280
⎪ 0.09 * 10 * 115.73 * = 6.94 cm2
⎩ 4200
Usando 6 φ 1/2" 6 * 1.27 = 7.62 cm2 > 6.94 cm2
∴CONFORME

51. En la dirección de longitud mayor:
hc = 80 - (2 * 4 + 1.27) = 70.73 cm
⎧ ⎛ 80 * 125 ⎞ 280
⎪ 0.3 * 10 * 70.73⎜ − 1⎟ = 2.65 cm2
⎝ 8424 ⎠ 4200
⎪
A sh ≥ ⎨
⎪ 280
⎪ 0.09 * 10 * 70.73 * = 4.24 cm2
⎩ 4200
Usando 4 φ 1/2" Ash = 4 * 1.27 = 5.08 cm2