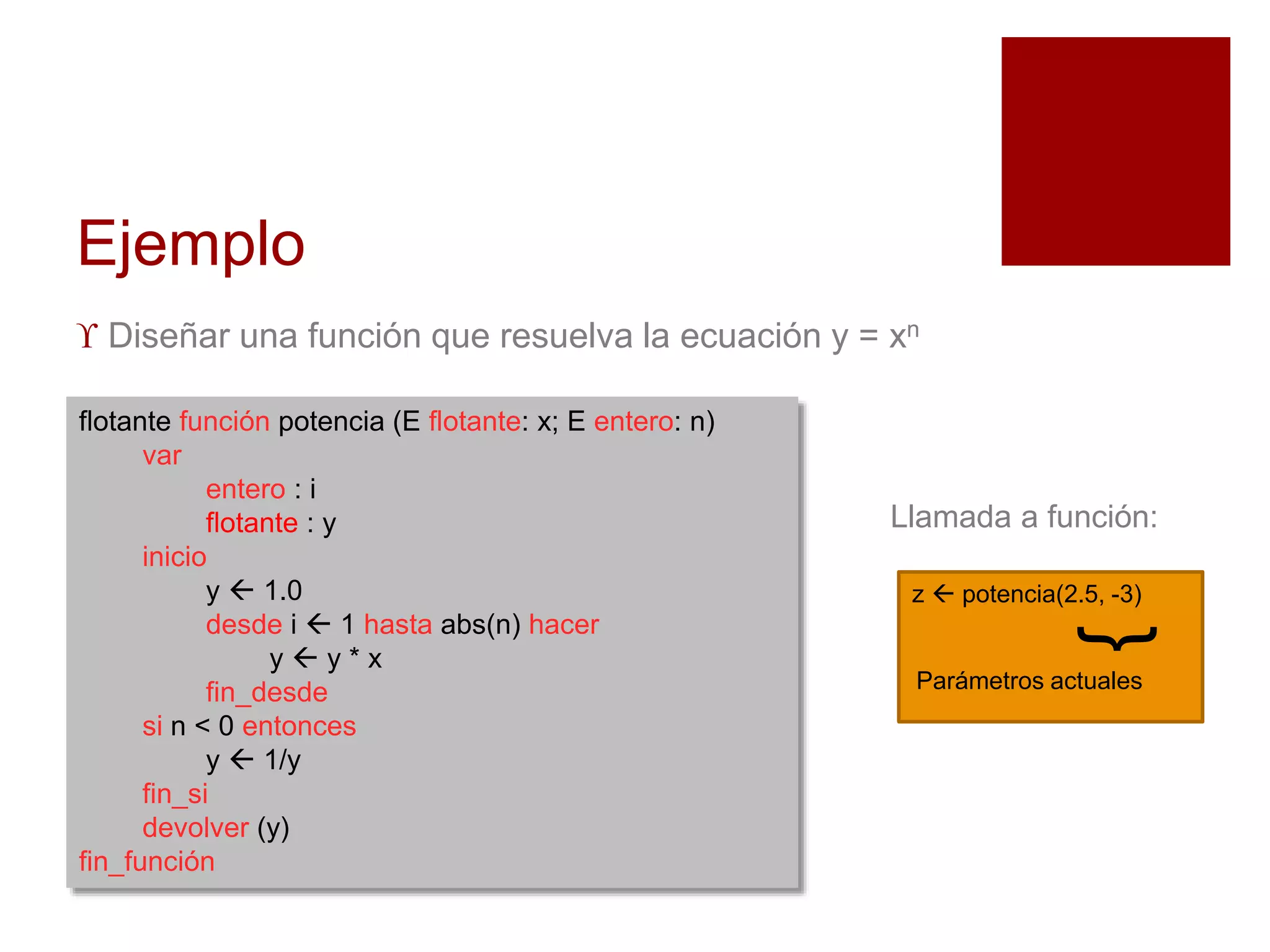
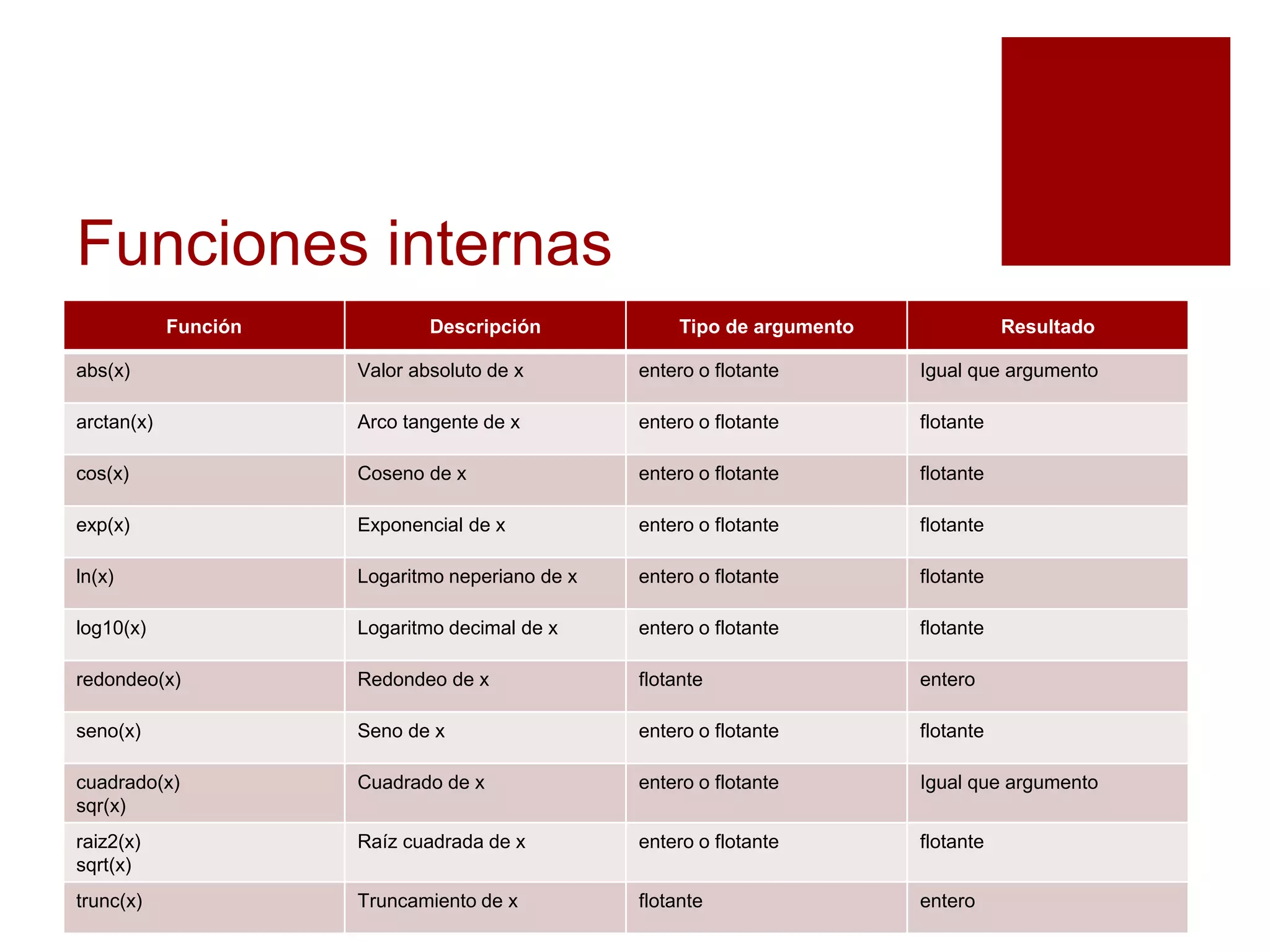
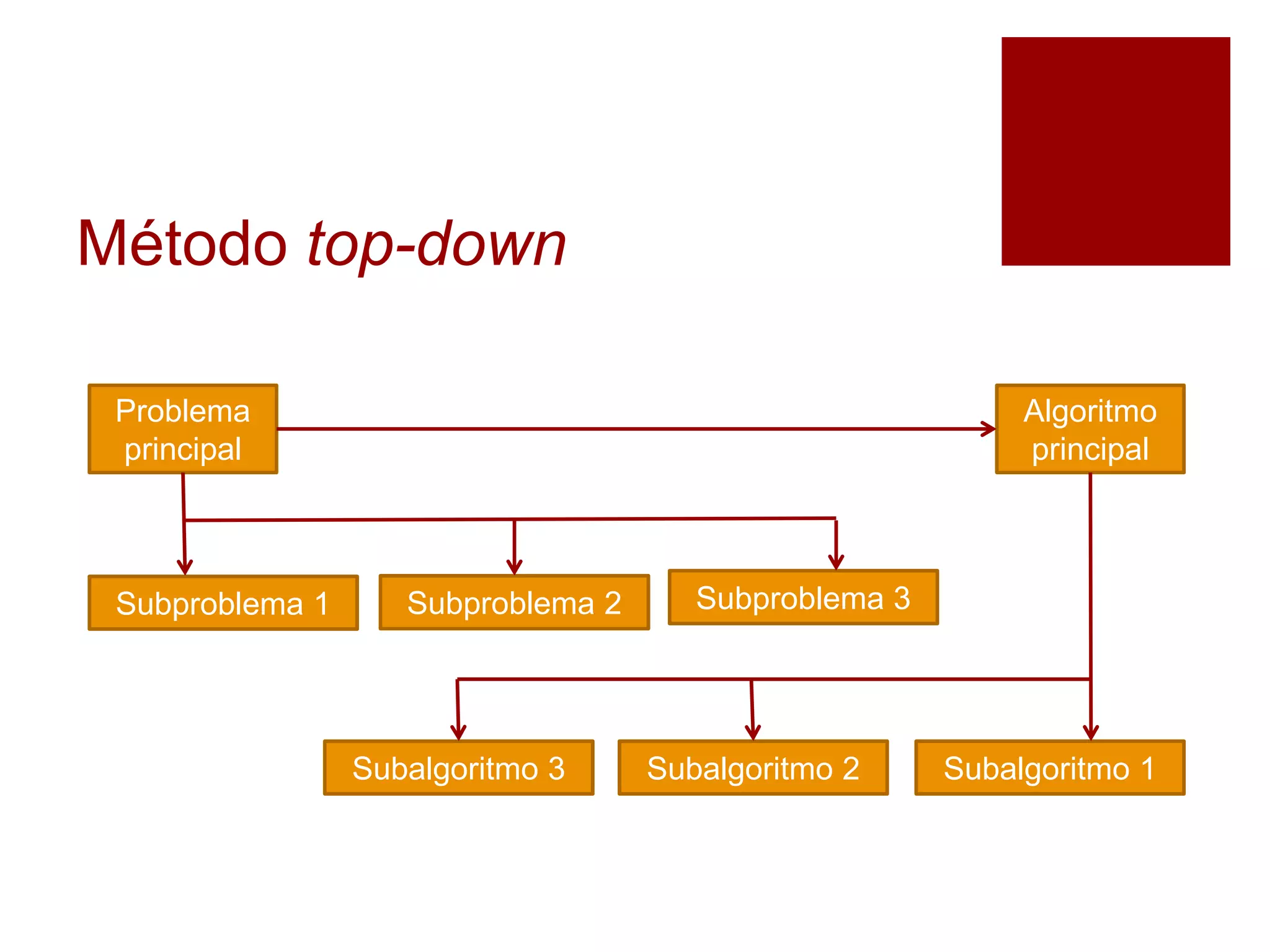
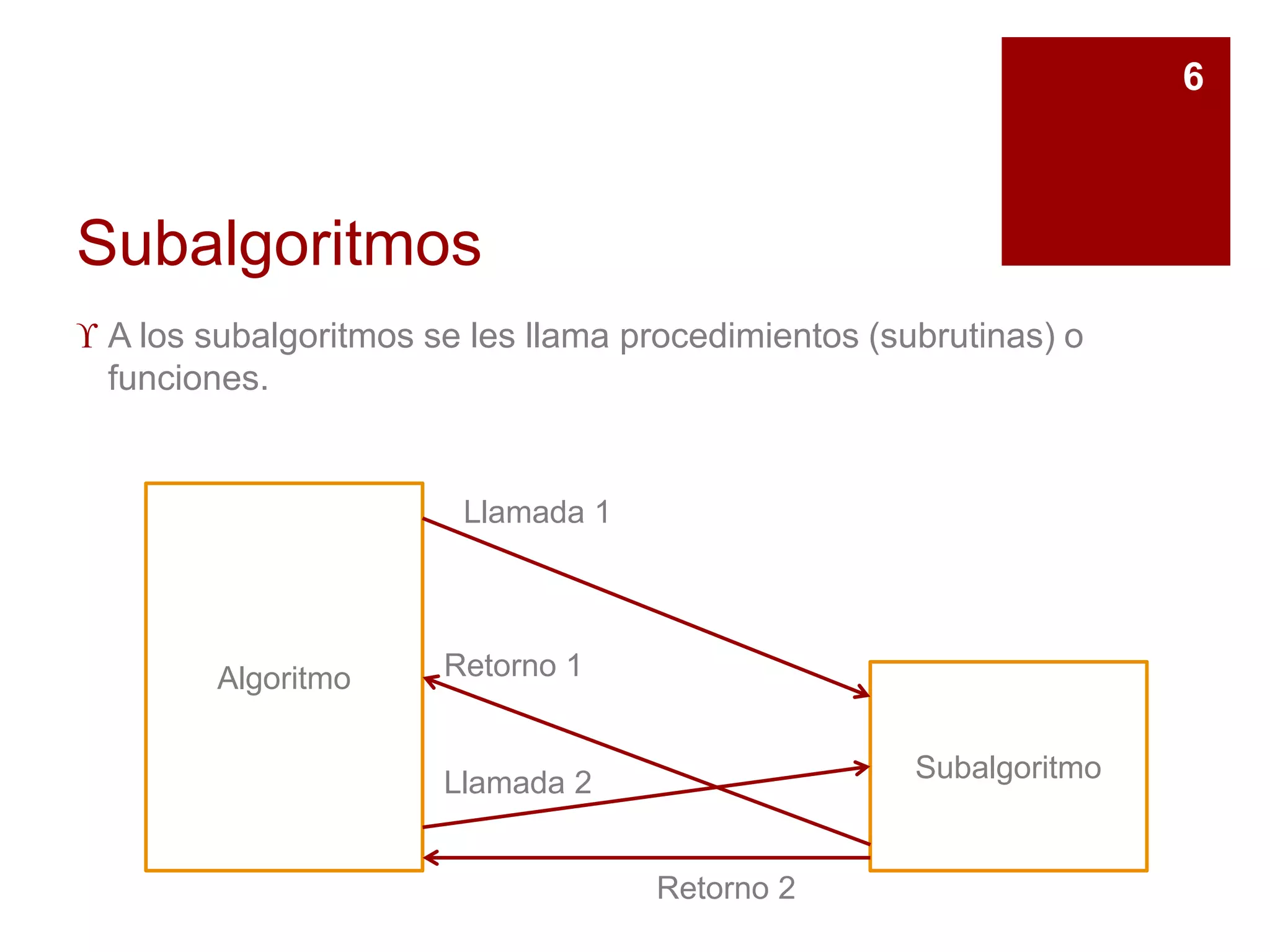
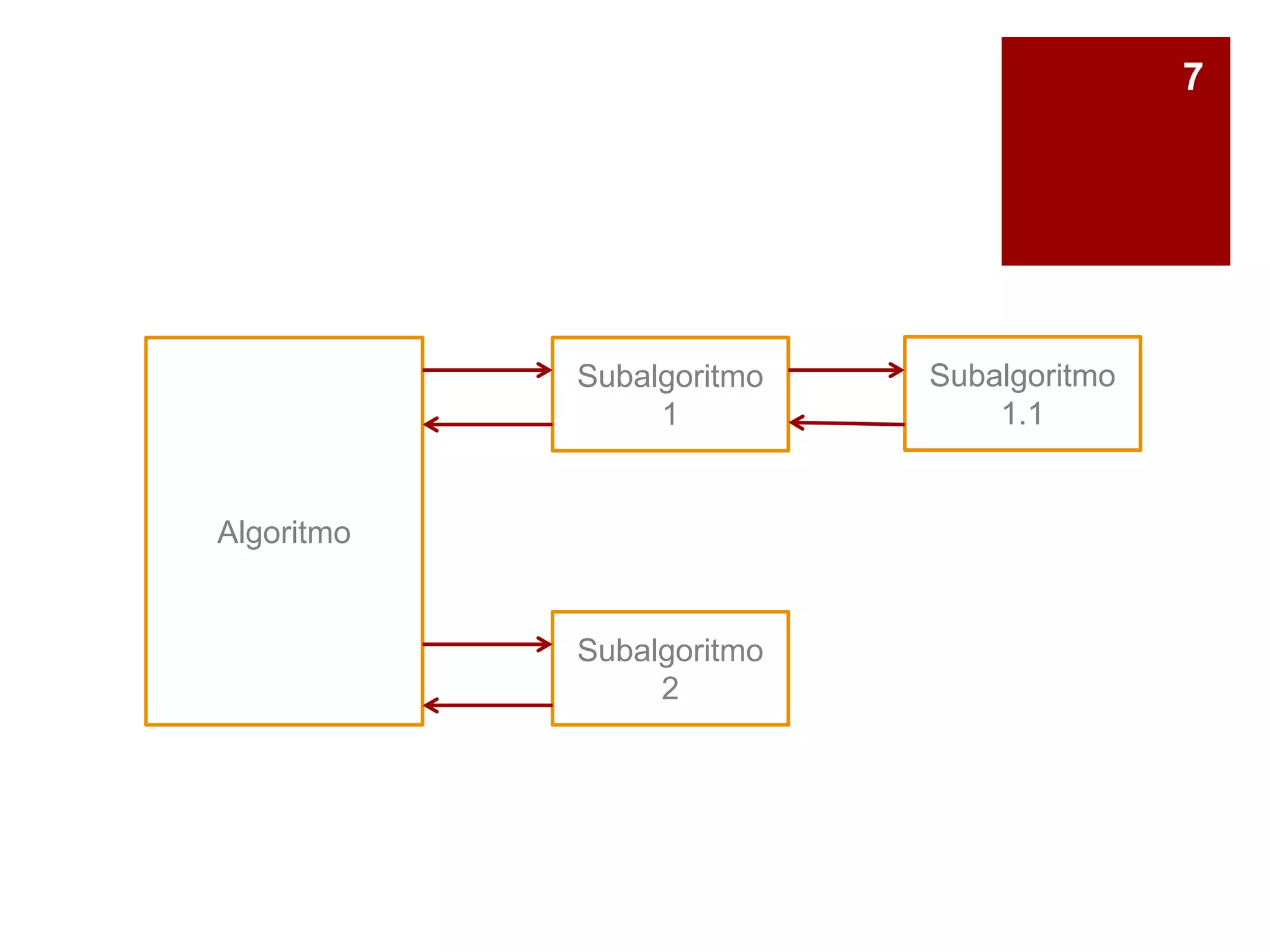
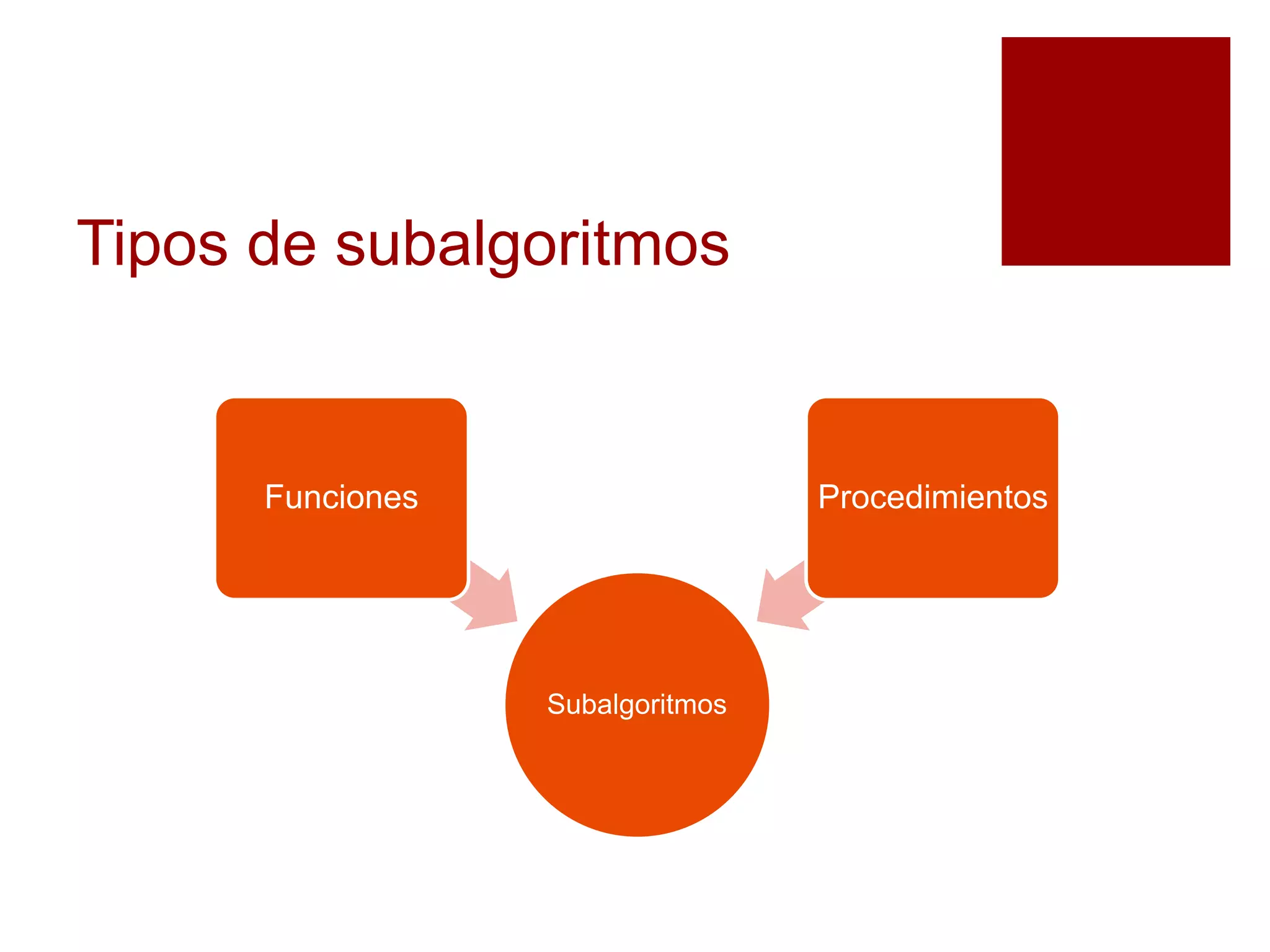
Este documento explica los subalgoritmos y su uso para dividir un problema complejo en subproblemas más sencillos. Define un subalgoritmo como una técnica para solucionar un problema dividiéndolo recursivamente en subproblemas más pequeños hasta que sean fáciles de resolver. Proporciona ejemplos de cómo dividir el cálculo del área de un rectángulo en subproblemas de entrada de datos, cálculo y salida de resultados. Explica también las diferencias entre funciones y procedimientos como tipos de subalgoritmos.

1. Subalgoritmos
Parte I
1
Ricardo Carrera Hernández
U n i v e r s i d a d

2. Subalgoritmo
 Técnica para solucionar un problema complejo dividiéndolo en
subproblemas o problemas más sencillos.
 Dividir estos problemas más sencillos en otros más simples
hasta que sean fáciles de resolver.
 Se le llama diseño top-down
2

3. Ejemplo
Calcular el área de un rectángulo:
Subproblema 1: entrada de datos altura y base
Subproblema 2: cálculo de la superficie
Subproblema 3: salida de resultados

4. Algoritmo
leer (altura, base) // entrada de datos
area  base * altura // cálculo de la superficie
escribir (base, altura, area) // salida de resultados

5. Método top-down
Problema
principal
Subproblema 1 Subproblema 2 Subproblema 3
Algoritmo
principal
Subalgoritmo 1Subalgoritmo 2Subalgoritmo 3

6. 6
 A los subalgoritmos se les llama procedimientos (subrutinas) o
funciones.
Subalgoritmos
Algoritmo
Subalgoritmo
Llamada 1
Retorno 1
Llamada 2
Retorno 2

7. 7
Algoritmo
Subalgoritmo
1
Subalgoritmo
1.1
Subalgoritmo
2

8. Tipos de subalgoritmos
Subalgoritmos
Funciones Procedimientos

9. 9
Funciones
 Matemáticamente una función es una operación que
toma uno o más valores llamados argumentos y
produce un valor llamado resultado.

10. Ejemplo
f es el nombre de la función
x es el argumento, ningún valor específico se asocia a x. Se le conoce
también como parámetro formal.
Para evaluar f debe darse a x un valor real. Con este valor debe
calcularse el resultado.
10
Si x = 3, entonces

11. Declaración de funciones
Tipo de dato función <nombre de función> ([lista de parámetros formales])
[declaraciones locales]
inicio
sentencia(s)
devolver (<expresión>)
fin_función
[<lista de parámetros formales>] son uno o más grupos de parámetros
separados por punto y coma. Cada grupo de argumentos se define de la
siguiente forma:
{ E | E/S } <tipo de dato> : <lista de parámetros>
E indica que el paso de parámetros se realiza por valor
E/S indica que el paso de parámetros se realiza por referencia

12. <nombre función (<lista de parámetros actuales>)
12
Llamada a función
La lista de parámetros actuales es una o varias variables o
expresiones separadas por comas que deben coincidir en número,
orden y tipo con la lita de parámetros formales de la declaración.

13. Ejemplo
 Diseñar una función que resuelva la ecuación y = xn
flotante función potencia (E flotante: x; E entero: n)
var
entero : i
flotante : y
inicio
y  1.0
desde i  1 hasta abs(n) hacer
y  y * x
fin_desde
si n < 0 entonces
y  1/y
fin_si
devolver (y)
fin_función
z  potencia(2.5, -3)
}
Parámetros actuales
Llamada a función:

14. Funciones internas
Función Descripción Tipo de argumento Resultado
abs(x) Valor absoluto de x entero o flotante Igual que argumento
arctan(x) Arco tangente de x entero o flotante flotante
cos(x) Coseno de x entero o flotante flotante
exp(x) Exponencial de x entero o flotante flotante
ln(x) Logaritmo neperiano de x entero o flotante flotante
log10(x) Logaritmo decimal de x entero o flotante flotante
redondeo(x) Redondeo de x flotante entero
seno(x) Seno de x entero o flotante flotante
cuadrado(x)
sqr(x)
Cuadrado de x entero o flotante Igual que argumento
raiz2(x)
sqrt(x)
Raíz cuadrada de x entero o flotante flotante
trunc(x) Truncamiento de x flotante entero

15. Ejercicios
1. Realizar el diseño de la función y = x3
2. Suponiendo que no se tuviera la función de la obtención del
valor absoluto de un número entero, realizar el diseño de la
función y = | x |

16. Subalgoritmos
Parte I
16
Ricardo Carrera Hernández
U n i v e r s i d a d