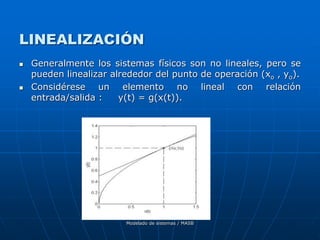
Este documento trata sobre el modelado de sistemas. Explica conceptos clave como ecuaciones diferenciales de sistemas físicos, linealización, transformada de Laplace, función de transferencia, diagramas de bloques y grafos de flujo de señales. También cubre sistemas multivariables y aplicaciones de MATLAB para el manejo de modelos.








![Modelado de sistemas / MASB
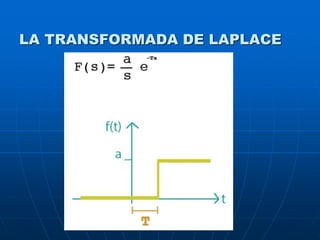
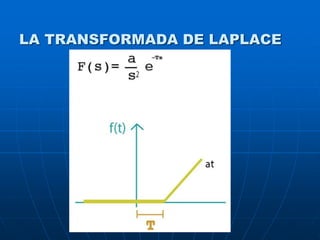
LA TRANSFORMADA DE LAPLACE
El método de la trasformada de Laplace (TL) permite
obtener la relación entrada / salida de un sistema LTI.
La trasformación de Laplace para una función del
tiempo f(t) tal que f(t)=0 para t<0, está dada por
Para su aplicación se han desarrollado tablas y se
utilizan teoremas y propiedades.
0
)
(
)
(
)]
(
[ dt
e
t
f
s
F
t
f
L st](https://image.slidesharecdn.com/2-210505052737/85/2-modelado-de-sistemas-10-320.jpg)


![Modelado de sistemas / MASB
LA TRANSFORMADA DE LAPLACE
)
(
lim
)
(
lim
)
(
lim
)
0
(
)
(
)
(
)
)
(
1
)
(
)
(
)
0
(
)
(
)
(
)
(
)
(
)]
(
)
(
[
0
0
2
1
2
1
0
2
1
2
1
s
sF
t
f
-
s
sF
f
-
s
F
s
F
dτ
(τ
τ)f
(t
f
dt
t
f
s
s
s
F
dt
t
f
L
f
s
sF
t
f
dt
d
L
s
bF
s
aF
t
bf
t
af
L
s
t
s
t
t
theorem
value
Final
theorem
value
Initial
n
Convolutio
n
Integratio
ation
Differenti
caling
Addition/S
Algunas propiedades y teoremas](https://image.slidesharecdn.com/2-210505052737/85/2-modelado-de-sistemas-13-320.jpg)



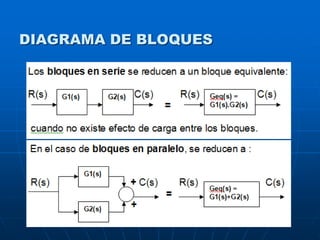
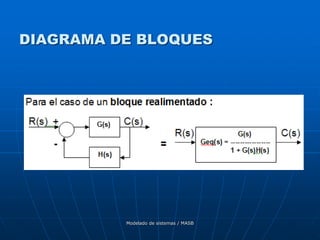
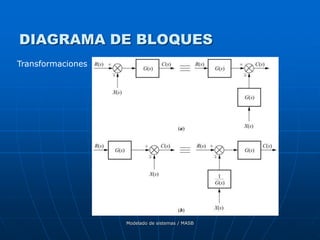
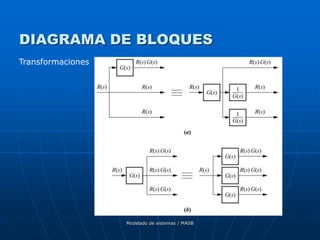
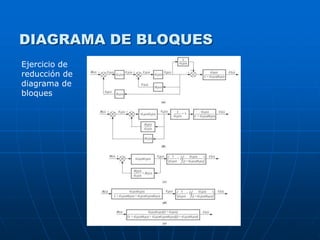

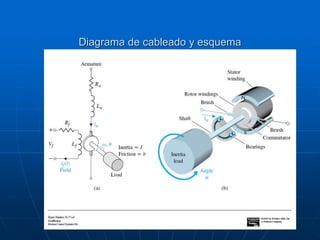
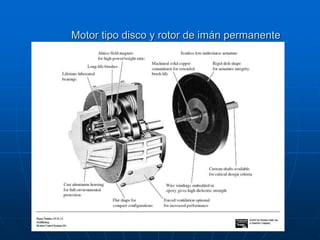
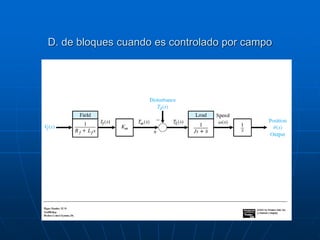
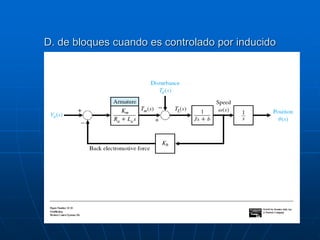






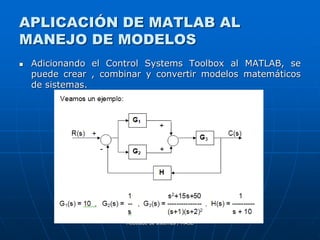
![Modelado de sistemas / MASB
APLICACIÓN DE MATLAB AL
MANEJO DE MODELOS
>> % Ingreso de las funciones de transferencia
>> g1=tf([10],[1]);
>> g2=tf([1],[1 0]);
>> g3=tf([1 15 50],poly([-1;-2;-2]));
>> h=zpk([],[-10],[1]);
>> % Reduccion del diagrama de bloques
>> gp=parallel(g1,g2);
>> gs=series(gp,g3);
>> geq=feedback(gs,h);](https://image.slidesharecdn.com/2-210505052737/85/2-modelado-de-sistemas-36-320.jpg)
