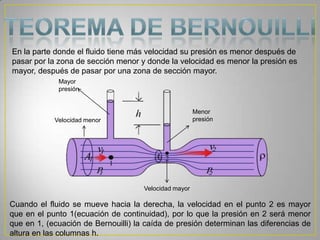
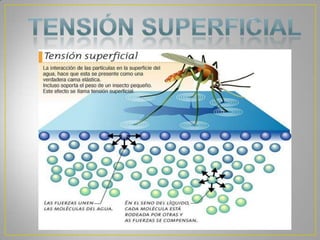
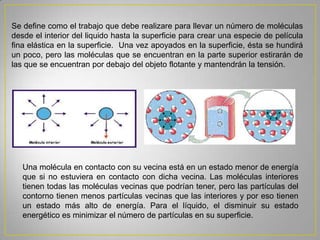
La hidrodinámica estudia el comportamiento de los fluidos en movimiento, considerando factores como la velocidad, presión y flujo. Supone que los líquidos son incompresibles, que la viscosidad tiene pérdidas mínimas, y que el flujo es estable. Analiza conceptos como la ecuación de continuidad, la conservación de la energía y la relación entre la velocidad, presión y altura de un fluido.

2. Es una parte de la Hidráulica que estudia el comportamiento de los fluidos en
movimiento.
Para ello se consideran entre otras cosas la
velocidad, presión, flujo y gasto del fluido. Para
el estudio de la hidrodinámica normalmente se
consideran tres aproximaciones importantes:
• Que el fluido es un líquido incompresible, es
decir, que su densidad no varía con el cambio
de presión, a diferencia de lo que ocurre con
los gases.
• Se considera despreciable la pérdida de
energía por la viscosidad (es la oposición de
un fluido a las deformaciones tangenciales. ),
ya que se supone que un líquido es óptimo
para fluir y esta pérdida es mucho menor
comparándola con la inercia de su
movimiento.
• Se supone que el flujo de los líquidos es en
régimen estable o estacionario, es decir, que
la velocidad del líquido en un punto es

3. El caudal es el volumen de un líquido que fluye por un
determinado tiempo (segundos). Representado con la letra
Q
tiempo
Volumen
Q CAUDA
L
OTRA FORMULA PARA EL CAUDAL ( Q = AxS )
Entonces mirando el dibujito, el líquido al moverse dentro del caño
recorre una cierta distancia d. Entonces al volumen que circula lo puedo
poner como:
Volumen = Sección del tubo x distancia.
El caudal es el volumen que circula
dividido el tiempo que pasa

4. Una canilla llena un balde de agua de 10 litros en 2 minutos.
min5
min2
10
l
Q
l
Q
tiempo
Volumen
Q
Caudal que
sale.
a)
seg
cm
seg
cm
l
v
cmv
cmv
SVQ
3,83
1*
1*5
*
2
60
5000
2
min
3
Velocidad del
agua a la
salida.

6. Ejemplo: El agua fluye a través de un diámetro de 6 m con una velocidad de
2m/seg. Calcular el radio que tiene el tubo en la otra parte si el agua circula con
una velocidad de 12 m/seg.
222
11
2
6
2
2744,28)3(*)1416.3(.1.
3
6
,
mmrAArea
mRadior
mdiámetrod
Entonces
md
De acuerdo con la ecuación de
continuidad:
2
22
2
2
2
2
2
2211
..
7124,4
)12(
)5488,56(
)12(*)2(*)2744,28(
3
rALuego
Am
A
Am
VAVA
s
m
s
m
s
m
s
m
2
2
2
2
2)1416.3(
)7124,4(
2
2
2
22,1
5,1
).1416.3()7124,4(
2
rm
rm
r
rm
m
R/ El radio del tubo en la
parte por la cual el agua
fluye a 12 m/seg es de
1,2cm.
Dato
s: s
m
V
md
2
6
1
1
s
m
V
rd
12
??
2
2

7. En la parte donde el fluido tiene más velocidad su presión es menor después de
pasar por la zona de sección menor y donde la velocidad es menor la presión es
mayor, después de pasar por una zona de sección mayor.
Mayor
presión
Menor
presiónVelocidad menor
Velocidad mayor
Cuando el fluido se mueve hacia la derecha, la velocidad en el punto 2 es mayor
que en el punto 1(ecuación de continuidad), por lo que la presión en 2 será menor
que en 1, (ecuación de Bernouilli) la caída de presión determinan las diferencias de
altura en las columnas h.

8. Ley de conservación de la energía en un fluido en movimiento
Un fluido en movimiento tiene 3 formas de energía que son:
2
2
22
1
21
2
12
1
1 ...... hgdvdPhgdvdP

En esta ecuación encontramos una relación entre la velocidad, la presión, y la altura
relativa de un fluido, también nos dice que si reducimos el área transversal de una
tubería para que aumente la velocidad del fluido, se reducirá la presión.

10. Una molécula en contacto con su vecina está en un estado menor de energía
que si no estuviera en contacto con dicha vecina. Las moléculas interiores
tienen todas las moléculas vecinas que podrían tener, pero las partículas del
contorno tienen menos partículas vecinas que las interiores y por eso tienen
un estado más alto de energía. Para el líquido, el disminuir su estado
energético es minimizar el número de partículas en su superficie.
Se define como el trabajo que debe realizare para llevar un número de moléculas
desde el interior del liquido hasta la superficie para crear una especie de película
fina elástica en la superficie. Una vez apoyados en la superficie, ésta se hundirá
un poco, pero las moléculas que se encuentran en la parte superior estirarán de
las que se encuentran por debajo del objeto flotante y mantendrán la tensión.

11. La tensión superficial mediante la letra griega gamma
A
d rev
Que es la cantidad de trabajo necesario para
llevar una molécula a la superficie.
Longitud
Fuerzatensión
erficialsup
Se puede interpretar con una fuerza por unidad de longitud o por lo
que es igual:
m
Nts
mNts 1
*
Unidades de Medida:
cm
Dyn
mJmNts 21
**