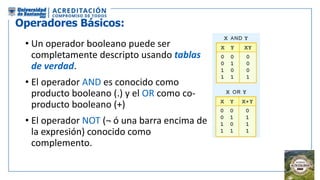
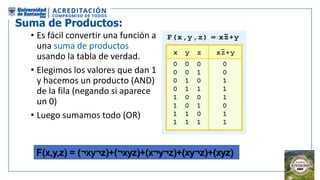
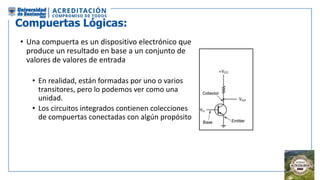
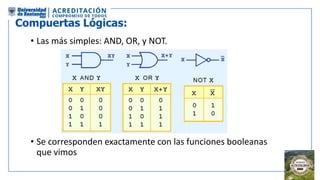
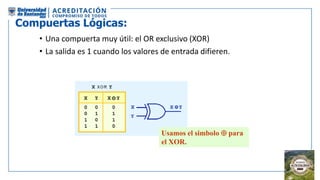
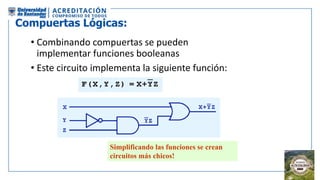
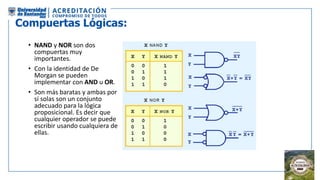
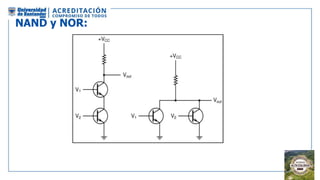
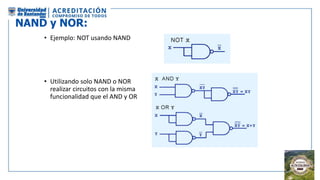
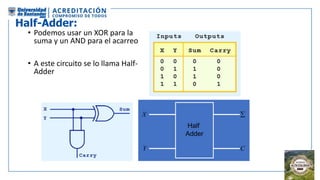
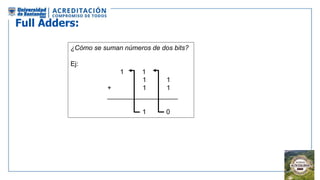
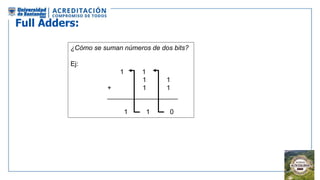
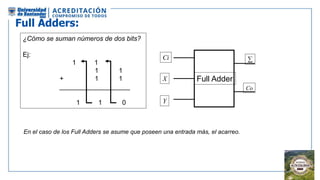
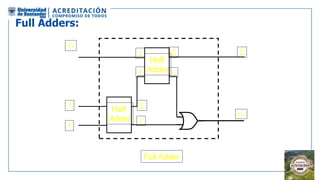
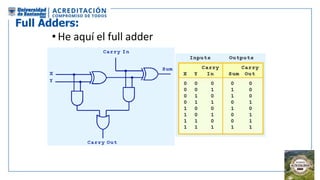
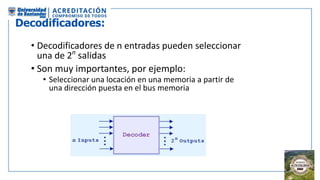
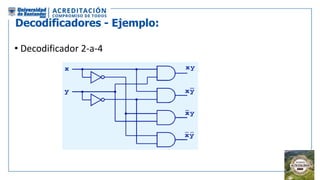
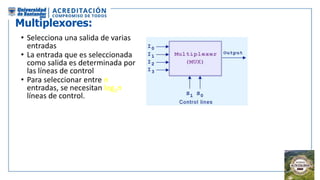
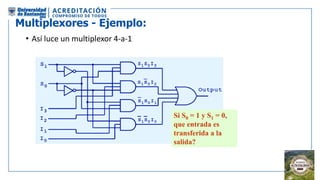
El documento aborda la organización de computadores mediante el análisis del álgebra de Boole y compuertas lógicas. Se explica cómo las computadoras almacenan datos en binario y cómo se realizan operaciones lógicas utilizando circuitos digitales, destacando la importancia de simplificar funciones booleanas. Además, se presentan conceptos como operadores booleanos, tablas de verdad, circuitos combinacionales, y dispositivos electrónicos como multiplexores y decodificadores.

2. Organización de Computadores
Algebra de Boole y Compuertas
Ingeniería de Software
2024

3. Representación de la información:
• La computadoras necesitan almacenar datos e instrucciones en memoria
• Sistema binario (sólo dos estados posibles)
• Por qué?
• Es mucho más sencillo identificar entre sólo dos estados
• Es menos propenso a errores

4. Lógica Digital:
• Los circuitos operan con valores [0, 1], que pueden ser interpretados
lógicamente como [Falso, Verdadero].
• Idea: implementar las operaciones lógicas y matemáticas combinando
circuitos

5. Algebra de Boole:
George Boole, desarrolló un sistema
algebraico para formalizar la lógica
proposicional. El libro se llama “Análisis
matemático de la lógica”.
George Boole
1815-1864
El sistema consiste en un cálculo para
resolver problemas de lógica
proposicional (dos valores posibles [0, 1]
y tres operaciones:
• AND (y)
• OR (o)
• NOT (no) )

6. Algebra de Boole:
Una variable booleana representa un valor de verdad, es decir,
TRUE o FALSE. Un bit es la unidad de información más pequeña
en una computadora, que representa 0 o 1. Un valor booleano
puede representarse completamente con un bit, pues false puede
ser 0 y true 1.tomar un bit

7. Operadores Básicos:
• Un operador booleano puede ser
completamente descripto usando tablas
de verdad.
• El operador AND es conocido como
producto booleano (.) y el OR como co-
producto booleano (+)
• El operador NOT (¬ ó una barra encima de
la expresión) conocido como
complemento.

8. Operadores Básicos:
• Tabla de verdad de esta
función:
• El NOT tiene más
precedencia que el resto de
los operadores
• Y el AND más que el OR

9. Identidades del algebra de Boole:
Las identidades del álgebra de Boole son proposiciones
equivalentes que se pueden demostrar utilizando tablas de
verdad. Son particularmente útiles para simplificar el diseño de
circuitos.
Identidad 1.A=A 0+A=A
Nula 0.A=0 1+A=1
Idempotencia A.A=A A+A=A
Inversa A.˜A=0 A+˜A=1
Conmutativa A.B=B.A A+B=B+A
Asociativa (A.B)C=A.(B.C) (A+B)+C=A+(B+C)
Distributiva A+B.C=(A+B).(A+C) A.(B+C)=A.B+A.C
Absorción A.(A+B)=A A+A.B=A
De Morgan ˜(A.B) = ˜A+˜B ˜(A+B) = ˜A.˜B

10. Fórmulas equivalentes:
• Varias fórmulas pueden tener la misma tabla de verdad
• Son lógicamente equivalentes
• En general se suelen elegir formas normales
• Suma de productos:
• F(x,y,z) = xy + xz +yz
• Producto de sumas:
• F(x,y,z) = (x+y) . (x+z) .(y+z)

11. Suma de Productos:
• Es fácil convertir una función a
una suma de productos
usando la tabla de verdad.
• Elegimos los valores que dan 1
y hacemos un producto (AND)
de la fila (negando si aparece
un 0)
• Luego sumamos todo (OR)
F(x,y,z) = (¬xy¬z)+(¬xyz)+(x¬y¬z)+(xy¬z)+(xyz)

12. Circuitos Booleanos:
• Las computadores digitales contienen circuitos que
implementan funciones booleanas
• Cuando más simple la función más chico el circuito
• Son más baratos, consumen menos, y en ocasiones son mas rápidos!
• Podemos usar las identidades del algebra de Boole para
reducir estas funciones.

13. Compuertas Lógicas:
• Una compuerta es un dispositivo electrónico que
produce un resultado en base a un conjunto de
valores de valores de entrada
• En realidad, están formadas por uno o varios
transitores, pero lo podemos ver como una
unidad.
• Los circuitos integrados contienen colecciones
de compuertas conectadas con algún propósito

14. Compuertas Lógicas:
• Las más simples: AND, OR, y NOT.
• Se corresponden exactamente con las funciones booleanas
que vimos

15. Compuertas Lógicas:
• Una compuerta muy útil: el OR exclusivo (XOR)
• La salida es 1 cuando los valores de entrada difieren.
Usamos el simbolo  para
el XOR.

16. Compuertas Lógicas:
• Combinando compuertas se pueden
implementar funciones booleanas
• Este circuito implementa la siguiente función:
Simplificando las funciones se crean
circuitos más chicos!

17. Compuertas Lógicas:
• NAND y NOR son dos
compuertas muy
importantes.
• Con la identidad de De
Morgan se pueden
implementar con AND u OR.
• Son más baratas y ambas por
sí solas son un conjunto
adecuado para la lógica
proposicional. Es decir que
cualquier operador se puede
escribir usando cualquiera de
ellas.

18. NAND y NOR:

19. NAND y NOR:
• Ejemplo: NOT usando NAND
• Utilizando solo NAND o NOR
realizar circuitos con la misma
funcionalidad que el AND y OR

20. Circuitos combinatorios:
• Producen una salida específica (casi) al instante que se le
aplican valores de entrada
• Implementan funciones booleanas
• La aritmética y la lógica de la CPU se implementan con estos
circuitos

21. Sumadores:
• Como podemos
construir un circuito
que sume dos bits X e Y?
• F(X,Y) = X + Y (suma
aritmética)
• Que pasa si X=1 e Y=1?

22. Half-Adder:
• Podemos usar un XOR para la
suma y un AND para el acarreo
• A este circuito se lo llama Half-
Adder
X
Y

C
Half
Adder

23. Full Adders:
¿Cómo se suman números de dos bits?
Ej:
1
1 1
+ 1 1
___________________
0

24. Full Adders:
¿Cómo se suman números de dos bits?
Ej:
1 1
1 1
+ 1 1
___________________
1 0

25. Full Adders:
¿Cómo se suman números de dos bits?
Ej:
1 1
1 1
+ 1 1
___________________
1 1 0

26. Full Adders:
¿Cómo se suman números de dos bits?
Ej:
1 1
1 1
+ 1 1
___________________
1 1 0
Full Adder
X
Y
Ci 
Co
En el caso de los Full Adders se asume que poseen una entrada más, el acarreo.

27. Full Adders:
Half
Adder
X
Y
Ci

Co
Full Adder
Half
Adder

C

C
X
Y

28. Full Adders:
• He aquí el full adder

29. Decodificadores:
• Decodificadores de n entradas pueden seleccionar
una de 2n
salidas
• Son muy importantes, por ejemplo:
• Seleccionar una locación en una memoria a partir de
una dirección puesta en el bus memoria

30. Decodificadores - Ejemplo:
• Decodificador 2-a-4

31. Multiplexores:
• Selecciona una salida de varias
entradas
• La entrada que es seleccionada
como salida es determinada por
las líneas de control
• Para seleccionar entre n
entradas, se necesitan log2n
líneas de control.

32. Multiplexores - Ejemplo:
• Así luce un multiplexor 4-a-1
Si S0 = 1 y S1 = 0,
que entrada es
transferida a la
salida?

33. Actividad:
• Realizar las siguientes sumas de binarios.
• 101000 + 100011 =
• 110101 + 110001 =
• 110110 + 100100 =
• 100110 + 111110 =
• 110011 + 101111 =
• 110011 + 101000 =