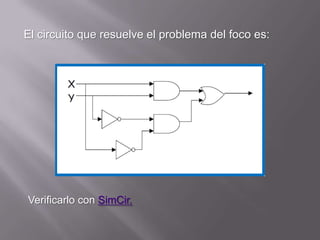
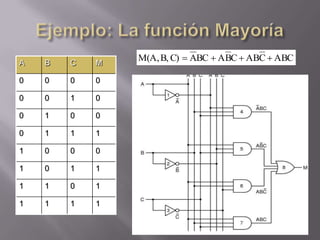
El documento describe conceptos básicos de lógica binaria y circuitos lógicos. Explica que las compuertas lógicas son bloques que producen señales binarias 1 o 0 en función de sus entradas y que se usan para implementar funciones lógicas en sistemas digitales. También resume que los microprocesadores contienen millones de transistores combinados para construir estructuras lógicas más complejas como sumadores y registros.

1. Nombre: Christian Giménez
C.I: 22323604
Informática (78)

2.  La lógica binaria tiene que ver con variables binarias y con
operaciones que toman un sentido lógico. La manipulación
de información binaria se hace por circuitos lógicos que se
denominan Compuertas.
 Las compuertas son bloques del hardware que producen
señales en binario 1 ó 0 cuando se satisfacen los requisitos
de entrada lógica. Las diversas compuertas lógicas se
encuentran comúnmente en sistemas de computadoras
digitales. Cada compuerta tiene un símbolo gráfico diferente
y su operación puede describirse por medio de una función
algebraica. Las relaciones entrada - salida de las variables
binarias para cada compuerta pueden representarse en
forma tabular en una tabla de verdad.

3.  La computadoras necesitan almacenar datos e
instrucciones en memoria
 Sistema binario (sólo dos estados posibles)
 Por qué?
 Es mucho más sencillo identificar entre sólo dos
estados
 Es menos propenso a errores

4.  Los circuitos operan con valores [0, 1], que
pueden ser interpretados lógicamente como
[Falso, Verdadero].
 Idea: implementar las operaciones lógicas y
matemáticas combinando circuitos.

5.  Los microprocesadores contienen millones de transistores
 Intel Pentium II: 7 millones
 Compaq Alpha 21264: 15 millones
 Intel Pentium III: 28 millones
 Lógicamente, cada transistor actúa como un interruptor
 Combinados para implementar funciones lógicas
 AND, OR, NOT
 Combinados para construir estructuras de mayor nivel
 Sumador, multiplexor, decodificador, registrador, …
 Combinados para construir procesadores
 LC-3
3-5

6.  Interruptor abierto:
 No hay corriente en el circuito
 Lámpara apagada
 Vsalida es +2.9V
 Interruptor cerrado:
 La corriente fluye
 Lámpara encendida
 Vsalida es 0V
Circuitos con interruptor pueden representar dos estados:
encendido/apagado, abierto/cerrado, voltaje/no voltaje.
3-6

7. George Boole, desarrolló un sistema
algebraico para formalizar la lógica
proposicional. El libro se llama “Análisis
matemático de la lógica”.
El sistema consiste en un cálculo para
resolver problemas de lógica
proposicional (dos valores posibles [0, 1]
George Boole y tres operaciones:
• AND (y)
1815-1864 • OR (o)
• NOT (no) )

8. Las variables Booleanas sólo toman
los valores binarios: 1 ó 0.
Una variable Booleana representa
un valor que puede tomar un bit,
que como vimos quiere decir:
Binary digIT

9.  Un operador booleano puede ser
completamente descrito usando
tablas de verdad.
 El operador AND es conocido como
producto booleano (.) y el OR como
co-producto booleano (+)
 El operador NOT (¬ ó una barra
encima de la expresión) conocido
como complemento.

10.  Tabla de verdad de
esta función:
 El NOT tiene más
precedencia que el resto
de los operadores
 Y el AND más que el
OR

11.  Varias fórmulas pueden tener la
misma tabla de verdad
 Son lógicamente equivalentes
 En general se suelen elegir formas
normales
 Suma de productos:
 F(x,y,z) = xy + xz +yz
 Producto de sumas:
 F(x,y,z) = (x+y) . (x+z) .(y+z)

12.  Las computadores digitales contienen
circuitos que implementan funciones
booleanas
 Cuando más simple la función más chico
el circuito
 Son más baratos, consumen menos, y en ocasiones
son mas rápidos!
 Podemos usar las identidades del algebra
de Boole para reducir estas funciones.

13.  Una compuerta es un dispositivo
electrónico que produce un resultado en
base a un conjunto de valores de entrada
 En realidad, están formadas por uno o
varios transistores, pero lo podemos ver
como una unidad.
 Los circuitos integrados contienen
colecciones de compuertas conectadas con
algún propósito

14.  Las más simples: AND, OR, y NOT.
 Se corresponden exactamente con las funciones
booleanas que vimos

15.  Una compuerta muy útil: el OR exclusivo (XOR)
 La salida es 1 cuando los valores de entrada
difieren.
Usamos el simbolo  para
el XOR.

16.  Combinando compuertas se pueden
implementar funciones booleanas
 Este circuito implementa la siguiente
función:
Simplificando las funciones se crean
circuitos más chicos!

17. Problema: un foco es controlado por dos
interruptores. Cada interruptor tiene dos
estados, abierto o cerrado. El foco debe prender
únicamente cuando ambos interruptores están
abiertos o cuando ambos están cerrados. Diseñe el
circuito para controlar el foco
• Entrada: el estado de cada uno de los dos
interruptores, donde 1 significa que un interruptor
está cerrado y 0 si está abierto
• Salida: 1 si el foco debe prender, de lo contrario 0

18. Tabla de verdad

19. El circuito que resuelve el problema del foco es:
Verificarlo con SimCir.

20. A B C M
M(A, B, C)  ABC  A BC  ABC  ABC
0 0 0 0
0 0 1 0
0 1 0 0
0 1 1 1
1 0 0 0
1 0 1 1
1 1 0 1
1 1 1 1