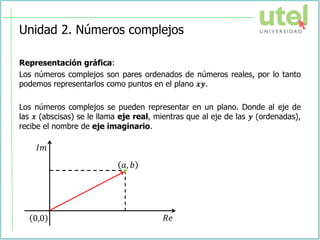
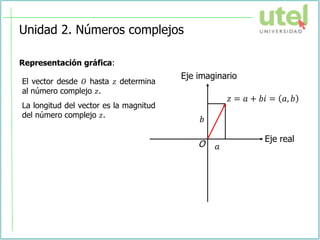
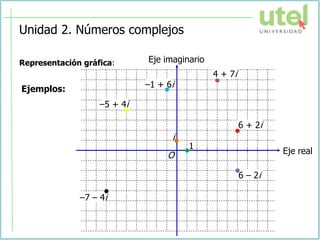
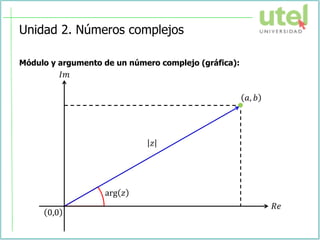
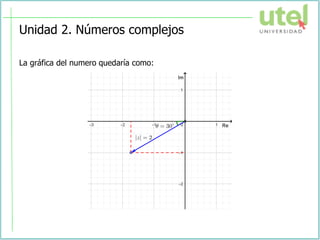
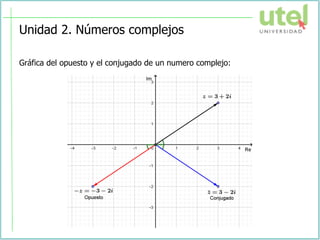
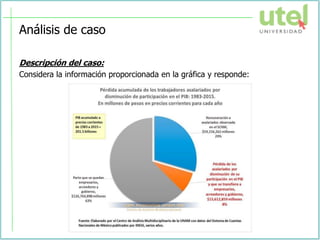
El documento presenta la sesión de la semana 2 del curso de Álgebra superior sobre números complejos. Se explican conceptos como números complejos, módulo y argumento, representación gráfica, operaciones y formas de los números complejos. Finalmente, se resuelven ejercicios como aplicación de los temas tratados.