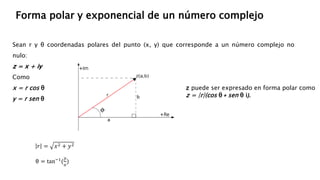
La unidad 1 se centra en los números complejos, sus representaciones y operaciones, esenciales en diversas áreas de las matemáticas y la ingeniería. Se introducen los números imaginarios y cómo resolver problemas con raíces de números negativos, así como las operaciones de suma, resta, multiplicación y división de números complejos. También se aborda la forma polar y exponencial de los números complejos y el Teorema de Moivre para elevar números complejos a potencias.

1. UNIDAD 1: NÚMEROS
COMPLEJOS
Números Complejos:: Utiliza los
números complejos, sus
representaciones y las
operaciones entre ellos para tener
una base de conocimiento a
utilizar en ecuaciones
diferenciales y en diferentes

2. Introducción
Los números complejos son una extensión de los números reales y se denotan
con la letra mayúscula C. Todo número complejo puede representarse como la suma
de un número real y uno imaginario, conservando todas las propiedades de los
números reales.
Los números complejos son importantes en el álgebra, variable compleja,
ecuaciones diferenciales, aerodinámica y electromagnetismo entre otras. Son
utilizados con especial énfasis en la matemática pura, mecánica cuántica y la
ingeniería, especialmente en la electrónica y sistemas computacionales.

3. Números imaginarios
Los números imaginarios surgen de la necesidad de resolver problemas que con
números reales son difíciles o imposibles de solucionar, uno de estos casos ocurre
cuando es necesario obtener las raíces cuadradas de un número negativo; por
ejemplo, al resolver la ecuación.

4. llegamos a que , pero esto no es un número real, así que dentro de los
números reales ésta ecuación no tiene solución. ¿Qué podemos hacer?, lo primero
que se puede intentar es agregar ese número al conjunto de los números reales y
listo. El problema es que deberíamos agregar muchos valores (todos los que pueda
tomar ), lo cual no es práctico; sin embargo, podemos hacer lo siguiente: cada vez
que tengamos una raíz de un número negativo lo separamos de la siguiente manera:
i
=
R i

5. Como este procedimiento siempre es válido y la es un número real, el único
problema sería con la , esto nos conduce a:

6. Con esto resolvemos completamente nuestro problema. Observemos que acabamos
de definir un conjunto de números muy grande; el de los imaginarios, que se
representa con la letra y cuyos elementos son de la forma donde es
cualquier número real e es el de nuestra definición anterior.
Una de las características importantes de los números imaginarios se observa cuando
los elevamos a potencias enteras. Veamos como se comportan:

8. Conclusión

9. Actividad

10. Investigar el origen del término número imaginario.

11. Ejercicio 1:
Considerando las características exponenciales del número imaginario, expresa en términos
de o 1.
Solución:
Podemos escribir como:
𝒊𝟑𝟗 = 𝑖4 9 +3 = (𝑖4)9𝑖3 ahora sabemos que 𝑖4 = 1, tenemos
𝑖39
= 1 9
𝑖3
, 𝑑𝑜𝑛𝑑𝑒 𝒊𝟑
= 𝒊𝟐
𝒊 = −i
𝑖39
= 1 9
−i = (1) –i
𝒊𝟑𝟗
= −i

12. Solución:
𝒊−𝟐𝟑 = 𝑖4 −6 +1 = (𝑖4)−6𝑖 ahora sabemos que 𝑖4 = 1, tenemos
𝑖−23
= 1 −6
𝑖 , 𝑑𝑜𝑛𝑑𝑒 𝒊 =−1
𝑖−23
=
𝟏
𝟏𝟔
(i)
𝒊−𝟐𝟑
= i
Ejercicio 2:
Considerando las características exponenciales del número imaginario, expresa en términos
de o 1.
Podemos escribir como:
𝑥−𝑛 =
1
𝑥𝑛
𝑖−23
=
𝟏
𝟏
(i) = 1(i)

13. Solución:
𝒊𝟎
= 𝑖4 0
= (𝑖4
)0
ahora sabemos que 𝑖4
= 1, tenemos
𝑖0 = 1 0
𝒊𝟎
= 1
Ejercicio 3:
Expresar en términos de o 1.
Podemos escribir como:

14. Ejercicios de tarea:
Expresar 𝒊𝟓𝟓
en términos de i o 1.
Expresar 𝒊−𝟒𝟑 en términos de i o 1.
Expresar 𝒊𝟐𝟐
en términos de i o 1.
Expresar 𝒊𝟐𝟕
en términos de i o 1.
Expresar 𝒊𝟐𝟎
en términos de i o 1.
Expresar 𝒊𝟐𝟔
en términos de i o 1.
Expresar 𝒊𝟑𝟓
en términos de i o 1.
Expresar 𝒊𝟓
en términos de i o 1.

15. Definición de números complejos

20. Operaciones con números complejos

21. Suma de números complejos

22. Solución:
Ejercicio
1:
Sumamos cada parte real y cada parte imaginaria
z1 + z2 + z3 = (3+1+0) + (- 4 + 2 -
1
4
)i
z1 + z2 + z3 = 4+(−
16
4
+
8
4
−
1
4
)i
z1 + z2 + z3 = 4+(−
9
4
)i
z1 + z2 + z3 = (4−
𝟗
𝟒
i)

23. Solución:
Ejercicio 2: Realizar la suma de Z¹ =2 + 8i, Z² =1 + i
Sumamos cada parte real y cada parte imaginaria
z1 + z2 = (2+1) + (8 + 1)i
z1 + z2 = (3) + (9)i
z1 + z2 = (3 + 9i)

24. Ejercicios de tarea:
3.- (7 – 3i) + (4 + 5i)
2.- (
3
2
− 5𝑖) + (4 + i)
1.- (-3 + 4i) + (6 – 3i)
4.- (-3 + 3i) + (7 - 2i)
5.- (5 + 2i) + (-8 + 3i)
6.- (2 + −4) + (3 - −16)

25. Resta de números complejos
La resta de números complejos también se realiza usando las mismas partes.
(a + bi) – (c + di) = (a - c) + (b - d)i

26. Solución:
Ejercicio 1: Realiza la resta de (2 - i) – (8 + 3i)
Restamos cada parte real y cada parte imaginaria
= (2 - i) – (8 + 3i)
= +(2 - i) – (8 + 3i)
= 2 - i – 8 - 3i
= - 6 – 4i

27. Solución:
Ejercicio 2: Realiza la resta de (-3 + 3i) – (7 - 2i)
Restamos cada parte real y cada parte imaginaria
= (-3 + 3i) – (7 - 2i)
= - 10 + 5i
= +(-3 + 3i) – (7 - 2i)
= -3 + 3i – 7 + 2i)

28. Ejercicios de tarea:
3.- (4 + i) - (3 - 2i) + (7 – 3i)
2.- (3 + 2𝑖) - (5 - 6i)
1.- (4 - 7i) - (6 – 5i)
4.- (
1
4
+
3
5
𝑖) – (
2
3
+
1
5
𝑖)
5.- (2 − 3𝑖) - (6 - 18i)

29. Multiplicación de números complejos
Nota: i² = -1

30. Solución:
Ejercicio 1: Realiza la multiplicación de (3 + 4i)(2 - 5i)
Resolvemos la multiplicación del polinomio
= (3 + 4i)(2 - 5i)
= 6 -15i + 8i –
20i²
= 6 -15i + 8i – 20(-1)
Nota: i² = -1
= 6 -15i + 8i + 20
= 26 - 7i

31. Solución:
Ejercicio 2: Realiza la multiplicación de (5 - 3i)(-4 - 7i)
Resolvemos la multiplicación del polinomio
= (5 - 3i)(-4 - 7i)
= -20 -35i + 12i +
21i²
= -20 -35i + 12i + 21(-1)
Nota: i² = -1
= -20 -35i + 12i - 21
= - 41 - 23i

32. Ejercicios de tarea:
3.- (6 + 8i)(4 + 2i)
2.- (2 +3𝑖)(5 - i)
1.- (3 + 2i)(5 + 6i)
4.- (-3 - 5i)(7 – 9i)
5.- (4 - i)(5 + 2i)

33. Solución:
Ejercicio 1: Simplificar la siguiente expresión i(1 -
i 𝟑)( 𝟑 + 𝒊)
= i(1 - i 𝟑)( 𝟑 + 𝒊)
= (i – (-1) 3)( 3 + 𝑖)
= (i + 3)( 3 + 𝑖)
Nota: i² = -1
= i 3 + i² + 3 3 + i 3
= (i – i² 3)( 3 + 𝑖)
= i 3 + i² + 3 ∗ 3 + i 3
Según la propiedad de los radicales
𝒏
𝒂. 𝒃 = 𝒂 𝒃

34. = i 3 + i² + 3 ∗ 3 + i 3
= i 3 + i² + 9 + i 3
= i 3 + i² + 3+ i 3 Nota: i² = -1
= i 3 + (-1) + 3+ i 3
= i 3 - 1 + 3+ i 3
= i 3 + 2 + i 3
= 2 + 2 3 𝑖
= 2 (1+ 3 𝑖)

35. Ejercicios de tarea:
1.- Si 𝑧 =
1
2
+
3
2
i , Determine Z² y
Z³
2.- Si 𝑧 =
3
2
+
1
2
𝑖, Determine Z² y Z³

36. 1.- Si 𝒛 =
𝟏
𝟐
+
𝟑
𝟐
i
Determine Z² y Z³

38. 2.- Si 𝑧 =
3
2
+
1
2
𝑖
Determine Z² y
Z³

40. División de números complejos
El producto de los números complejos c + di y c - di es un numero real positivo:
(c + di)(c - di) = 𝒄𝟐 − 𝒄𝒅𝒊 + 𝒄𝒅𝒊 − 𝒅𝟐𝒊𝟐 y sabemos que 𝑖2 = −1
Entonces tenemos: (c + di)(c - di) = 𝐜𝟐+ 𝐝𝟐
Entonces introduciremos la siguiente definición para describir esta relación especial.

41. 𝒂+𝒃𝒊
𝒄+𝒅𝒊
=
𝒂+𝒃𝒊
𝒄+𝒅𝒊
∗
𝒄−𝒅𝒊
𝒄−𝒅𝒊
=
𝒂𝒄−𝒂𝒅𝒊+𝒃𝒄𝒊−𝒃𝒅𝒊𝟐
𝒄𝟐+𝒅𝟐 =
𝒂𝒄−𝒂𝒅𝒊+𝒃𝒄𝒊+𝒃𝒅
𝒄𝟐+𝒅𝟐 =
𝒂𝒄+𝒃𝒅 + 𝒃𝒄−𝒂𝒅 𝒊
𝒄𝟐+𝒅𝟐
Definición de conjugado complejo
El conjugado complejo del número complejo:
Z = c + di es 𝑧 = 𝑐 + 𝑑𝑖 = c – di
Z = c - di es 𝑧 = 𝑐 − 𝑑𝑖 = c + di

42. Solución
:
Ejercicio 1: Realiza la división de :
𝟑+𝟐𝒊
𝟏−𝟐𝒊
Debemos encontrar el conjugado del denominador, tal como lo dice la propiedad:
𝟑 + 𝟐𝒊
𝟏 − 𝟐𝒊
=
3 + 2𝑖
1 − 2𝑖
∗
1 + 2𝑖
1 + 2𝑖
Nota: i² = -1
=
3 + 6𝑖 + 2𝑖 + 4𝑖2
(1)2 + (2)2
Resolvemos la multiplicación como un polinomio, termino a termino
=
3 + 6𝑖 + 2𝑖 + 4(−1)
(1)2 + (2)2
=
3 + 6𝑖 + 2𝑖 − 4
(1)2 + (2)2
=
3 + 6𝑖 + 2𝑖 − 4
1 + 4
Sumamos parte real y parte
imaginaria por separado y
simplificamos denominador
=
−1 + 8𝑖
5
Usamos la propiedad distributiva
de la división
=
−𝟏
𝟓
+
𝟖𝒊
𝟓
Resolvemos el
denominador

43. Ejercicios de tarea:

44. Problemario

45. Sean r y θ coordenadas polares del punto (x, y) que corresponde a un número complejo no
nulo:
z = x + iy
Como
x = r cos θ
y = r sen θ
z puede ser expresado en forma polar como
z = |r|(cos θ + sen θ i).
Forma polar y exponencial de un número complejo
𝑟 = 𝑥2 + 𝑦2
θ = tan−1
(
𝑦
𝑥
)

46. Donde:
A r se le conoce como módulo de z y mide la distancia del número complejo al
origen, por lo tanto debe ser positivo.
El ángulo θ se conoce como argumento de z y se pide que tenga su valor entre cero y 2 ¶
porque las funciones trigonométricas son cíclicas con periodo igual a 2 ¶, es decir

47. Tomando en cuenta que un ángulo positivo se mide con un giro en sentido contrario a las
manecillas del reloj.
De igual manera podemos representar un numero complejo dentro del plano polar complejo
(conociendo el ángulo que forma con el eje real y la distancia a la que se encuentra del origen).

48. Solución
:
Ejercicio 1: Convertir de rectangular a polar : z = 5 – 5i
Debemos encontrar el módulo de z
𝑟 = (5)2+(−5)2 = 25 + 25 = 𝟓𝟎 = 7.071067812
𝑟 = 𝑥2 + 𝑦2
θ = tan−1(
𝑦
𝑥
) = tan−1(
−5
5
) = −𝟒𝟓
Como el 5,-5 se localizan en el cuadrante 4 del plano cartesiano, entonces restamos a los 360 -45
θ = 360 − 𝟒𝟓 = 𝟑𝟏𝟓
θ = 𝟑𝟏𝟓º
P = ( 𝟓𝟎, 𝟑𝟏𝟓º)

49. Ejercicio 1: Graficamos

50. Solución
:
Ejercicio 2: Convertir de rectangular a polar : z = - 3 + i
Debemos encontrar el módulo de z
𝑟 = (−3)2+(1)2 = 9 + 1 = 𝟏𝟎 = 3.16227766
𝑟 = 𝑥2 + 𝑦2
θ = tan−1
(
𝑦
𝑥
) = tan−1
(
1
3
) = −𝟏𝟖. 𝟒𝟑𝟒𝟗𝟒𝟖𝟖𝟐
Como el -3,1 se localizan en el cuadrante 2 del plano cartesiano, entonces restamos a los 180 - 18.43
θ = 𝟏𝟖𝟎 − 𝟏𝟖. 𝟒𝟑𝟒𝟗𝟒𝟖𝟖𝟐 = 𝟏𝟔𝟏. 𝟓𝟔𝟓𝟎𝟓𝟏𝟐
θ = 𝟏𝟔𝟏. 𝟓𝟔𝟓𝟎𝟓𝟏𝟐º
P = ( 𝟏𝟎, 𝟏𝟔𝟏. 𝟓𝟔𝟓𝟎𝟓𝟏𝟐º)

51. Ejercicio 2: Graficamos

52. Solución
:
Ejercicio 3: Convertir de polar a rectangular : p = (6, 30 º)
z = |r|(cos θ + sen θ i)
z = 6(cos 30 + sen 30 i)
x = 6(cos 30 ) = 5.196152423 = 3 𝟑
y = 6(sen 30 i) = 3
z = (3 𝟑, 𝟑𝒊)

53. Ejercicio 3: Graficamos

54. Ejercicios de tarea:
CONVIERTE A COORDENADAS POLARES LOS SIGUIENTES PUNTOS:
Z= ( 3, 5i)
Z= (-3, 4i)
Z= (1, 7i)
Z= (-6, 3i)
Z= (5, 2i)
Realizar la gráfica correspondiente

55. Ejercicios de tarea:
CONVIERTE A COORDENADAS RECTANGULARES LOS SIGUIENTES
PUNTOS:
P= (4, 30º)
P= (3, 70º)
P= (6, 130º)
P= (5, 90º)
P= (7, 45º)
Realizar la gráfica correspondiente

56. En el teorema se establece que cuando se tiene un número complejo en la forma polar z = rƟ,
en la que r es el módulo del número complejo z, el ángulo Ɵ es la amplitud del número
complejo en el que 0 ≤ Ɵ ≤ 2π, de forma que para poder calcular su n-ésima potencia no se
necesita múltiplicarlo por sí mismo n-veces.
La fórmula del teorema de Moivre fue creada y nombrada por Abraham de Moivre, quien
afirmaba que un número complejo (especialmente en el caso cualquier número real) x y para
cualquier entero n se puede verificar que:
z = |r|(cos θ + sen θ i)
Entonces
z𝒏= |r|
𝒏
(cos θ(n ) + sen θ(n ) i)
Teorema de Moivre, potencias de números
complejos

57. Solución
:
Ejercicio 1: Aplicando el teorema de Moivre, calcular
𝒛 = (𝟐 + 𝟐𝒊)𝟖
𝑟 = 𝑥2 + 𝑦2 = 22 + 22 = 4 + 4 = 𝟖
Utilizando el teorema de Pitágoras encontramos el
modulo de r
θ = tan−1
(
𝑦
𝑥
) = tan−1
(
2
2
) = 𝟒𝟓
z8
= ( 8)8
(cos 45(8 ) + sen 45(8 ) i)
z8
= 4096 (cos 360 + sen 360 i)
z𝒏= |r|
𝒏
(cos θ(n ) + sen θ(n ) i)
z8
= 4096 (1 + 0 i)
z8= 4096 (1)
z𝟖= 𝟒𝟎𝟗𝟔
Utilizando el teorema de Moivre
para elevar a potencia.

58. Ejercicios de tarea:
Aplicando el teorema de Moivre extraer la potencias de los
siguientes números complejos.
𝒛 = ( 𝟑 + 𝒊)−𝟒
𝒛 = (𝟔 − 𝟕𝒊)𝟐
𝒛 = (𝟑 + 𝟓𝒊)𝟑
𝒛 = (−𝟒 − 𝟒𝒊)𝟏𝟓
𝒛 = (𝟒 + 𝟒 𝟑 𝒊)𝟒