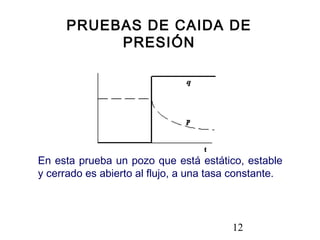
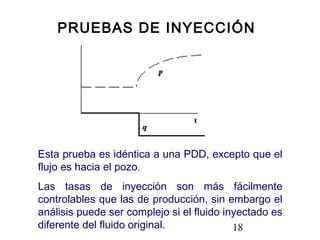
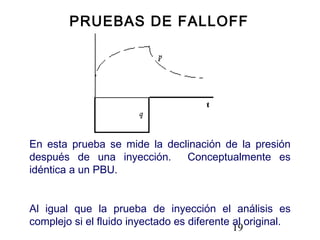
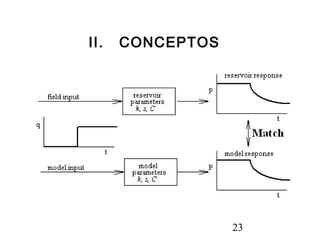
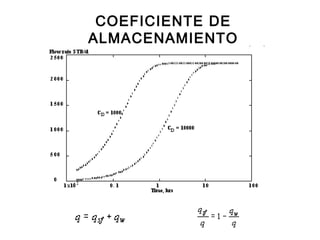
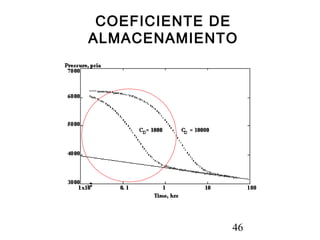
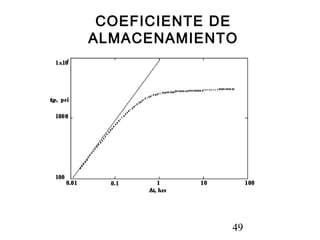
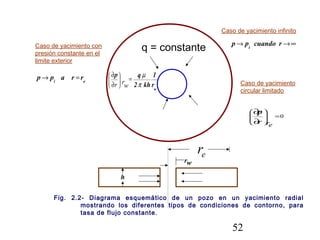
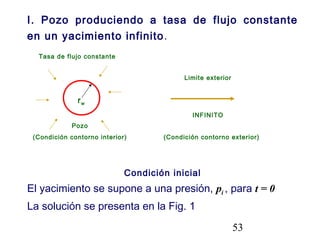
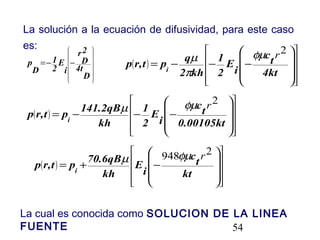
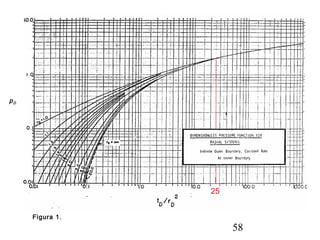
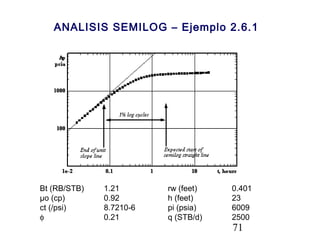
Este documento describe los análisis de pruebas de presión para evaluar yacimientos petrolíferos. Las pruebas de presión permiten determinar la conductividad, presión inicial y límites del yacimiento. También se utilizan para monitorear el desempeño de los pozos y predecir la producción a largo plazo. El documento explica conceptos como la ley de Darcy, ecuaciones de flujo y tipos comunes de pruebas como caída de presión y ascenso de presión.

1. 1
ANALISIS DE
PRUEBAS DE
PRESION

2. 2
•EVALUACION DEL YACIMIENTO
•MANEJO DEL YACIMIENTO
•DESCRIPCION DEL YACIMIENTO
I. OBJETIVOS

3. 3
Para tomar la decisión de poner en producción un
yacimiento se debe conocer:
•Su capacidad de entrega
•Propiedades
•Tamaño
A través de las pruebas de presión, se puede
determinar: conductividad (kh), la presión inicial (pi)
y los límites del yacimiento.
EVALUACION DEL YACIMIENTO

4. 4
•La conductividad (kh) gobierna qué tan rápido los
fluidos pueden fluir al pozo. Por lo cual es un
parámetro a tener en cuenta para diseñar el
espaciamiento y el número de pozos.
•La presión nos indica que tanta energía tiene el
yacimiento y permite pronosticar por cuanto tiempo
el yacimiento podrá producir.
EVALUACION DEL YACIMIENTO

5. 5
•Las presiones en la vecindad del pozo son
afectadas por la perforación y por la producción, y
puede ser bien diferente del valor de la presión del
yacimiento. La interpretación de las pruebas de
pozo permite inferir las presiones a distancias
considerables del pozo a partir de las presiones
locales que se miden en los pozos.
•El análisis de los límites permite determinar cuanto
fluido está presente en el yacimiento y si los límites
son cerrados o abiertos.
EVALUACION DEL YACIMIENTO

6. 6
Durante la vida del yacimiento se debe monitorear
el desempeño y las condiciones de los pozos.
Es útil monitorear los cambios en la presión
promedio del yacimiento de tal manera que se
puedan refinar los pronósticos de desempeño del
yacimiento.
Al monitorear los pozos es posible determinar los
candidatos para trabajos de workover o de
estimulación.
MANEJO DEL YACIMIENTO

7. 7
Las pruebas de presión pueden ser interpretadas
para estimar las propiedades globales del
yacimiento, ya que dichas pruebas no son
sensitivas a las heterogeneidades de escala local.
DESCRIPCION DEL
YACIMIENTO

8. 8
El caso en el cual la presión de un pozo fluyendo
es tratada como constante y la tasa de producción
declina, se conoce comúnmente como análisis de
curvas de declinación.
Fundamentalmente no hay diferencia entre el
análisis de la transiente de presión y el análisis de
curvas de declinación; sin embargo, hay
consideraciones practicas que separan los dos
análisis.
ANALISIS DE CURVAS DE
DECLINACIÓN

9. 9
Puesto que la tasa de flujo es fácil de controlar en
una prueba corta, las pruebas de transiente de
presión (PDD, PBU) son conducidas sólo durante
unas pocas horas o días.
Dichas pruebas se usan para obtener las
condiciones cerca de la cara del pozo, tales como
kh, almacenamiento y daño (skin)
ANALISIS DE CURVAS DE
DECLINACIÓN

10. 10
Durante pruebas de producción de larga duración,
la presión es a menudo controlada por equipos y
las tasas son monitoreadas a largo plazo (meses y
años) para el análisis de las curvas de declinación.
Por lo tanto, el análisis de las curvas de declinación
permiten obtener diagnósticos de efectos a largo
plazo, como el volumen del yacimiento.
ANALISIS DE CURVAS DE
DECLINACIÓN

11. 11
•Pruebas de caída de presión (PDD)
•Pruebas de ascenso de presión (PBU)
•Pruebas de inyección
•Pruebas de falloff
•Pruebas de interferencia
•Drill Stem Test (DST)
TIPOS DE PRUEBAS

12. 12
En esta prueba un pozo que está estático, estable
y cerrado es abierto al flujo, a una tasa constante.
PRUEBAS DE CAIDA DE
PRESIÓN

13. 13
Es difícil hacer que el pozo fluya a tasa constante,
aun después de que ha estado (mas o menos)
estabilizado
•La condición inicial del pozo puede que no sea
estática o estable, especialmente si el pozo ha sido
perforado recientemente o ha estado previamente
en flujo.
PRUEBAS DE CAIDA DE
PRESIÓN
Desventajas

14. 14
Un PDD es un buen método para probar los límites
del yacimiento ya que el tiempo requerido para
observar la respuesta de un límite es largo y las
fluctuaciones operacionales en la tasa de flujo son
menos importantes sobre grandes periodos de
tiempo.
PRUEBAS DE CAIDA DE
PRESIÓN
Ventajas

15. 15
En esta prueba un pozo que ha estado fluyendo
(idealmente a tasa constante) es cerrado, y se
mide el aumento de la presión en el fondo del
pozo.
PRUEBAS DE ASCENSO DE
PRESIÓN

16. 16
•Puede ser difícil alcanzar una tasa de producción
constante antes de que el pozo sea cerrado. En
particular, puede ser necesario cerrar el pozo para
bajar la herramienta.
•La pérdida de producción mientras el pozo está
cerrado.
PRUEBAS DE ASCENSO DE
PRESIÓN - Desventajas

17. 17
La principal ventaja es que la condición requerida
de tasa constante es lograda fácilmente ya que el
pozo tiene una tasa de producción igual a cero.
PRUEBAS DE ASCENSO DE
PRESIÓN - Ventajas

18. 18
Esta prueba es idéntica a una PDD, excepto que el
flujo es hacia el pozo.
Las tasas de inyección son más fácilmente
controlables que las de producción, sin embargo el
análisis puede ser complejo si el fluido inyectado es
diferente del fluido original.
PRUEBAS DE INYECCIÓN

19. 19
En esta prueba se mide la declinación de la presión
después de una inyección. Conceptualmente es
idéntica a un PBU.
Al igual que la prueba de inyección el análisis es
complejo si el fluido inyectado es diferente al original.
PRUEBAS DE FALLOFF

20. 20
En esta prueba un pozo se pone en producción y la
presión se registra en un pozo (o pozos ) diferente(s).
Esta prueba es útil para caracterizar las propiedades
del yacimiento en una escala más grande que en una
prueba convencional.
Dado que los cambios de presión a una distancia
considerable del pozo productor son mucho mas
pequeños se requieren equipos sofisticados y tiempo
considerable.
PRUEBAS DE INTERFERENCIA

21. 21
En esta prueba se usa una herramienta especial
montada al final de la tubería de perforación.
En un DST la secuencia común es: producir, cerrar,
producir de nuevo y cerrar de nuevo.
Esta prueba por lo general es de corta duración ya
que, como el cierre se hace en el fondo, se evitan los
efectos del almacenamiento
DST

22. 22
Las pruebas de presión pueden ser usadas para
obtener:
•Presión promedio del yacimiento del área de drenaje
•Permeabilidad de la formación
•Daño
•Efectividad de una estimulación o tratamiento
•Conectividad entre pozos
•Estructuras geológicas
APLICACION

23. 23
II. CONCEPTOS

24. 24
LEY DE CONSERVACION
DE LA MASA
Fig. 2.1- Elemento de volumen sobre el cual
se aplica el balance de masa
pozo
( )ruru ρρ ∆+ ruρ
h
θ
r r∆

25. 25
Cantidad de masa que entra al sistema menos cantidad
masa que sale del sistema es igual a Acumulación de
masa en el sistema.
Aplicando esta ley al elemento de la Fig. 2.1,
simplificando y tomando límites cuando y
Se obtiene la ecuación de continuidad:
( ) ( )
t
u
1
r
∂
∂
−=
∂
∂ ρφ
ρr
rr
t∆ 0r →∆
(2-1)

26. 26
r
pk
∂
∂−=
µru
La Ley de Darcy es:
tr
pkr
rr ∂
∂
=
∂
∂
∂
∂ 














 φρ
µρ1
Sustituyendo (2-2) en (2-1) obtenemos
(2-2)
(2-3)
tr
pkr
rr ∂
∂
=
∂
∂
∂
∂ 














 φρ
µρ
000264.0
11

27. 27
Consideramos un fluido de comprensibilidad
constante: un líquido, por ejemplo: petróleo o agua.
Ecuación de estado
T = cte. Proceso isotérmico luego, (2-4) es una
ecuación diferencial de 1er
grado, 1er
orden ordinaria:
integrando (2-4) se obtiene
El subíndice sc, se refiere a condiciones standard
TT
p
1
p
V
V
1
-c 





∂
∂
=





∂
∂
=
ρ
ρ
(2-4)
ρ
ρρρ dcd;
d
dc == p
p
( ) ( )scppc
epp
−
== sc;- ρρ
ρ
ρ
sc
lnscc (2-5)

28. 28
El 2do
miembro de la ec. 2-1 puede ser escrito:
La ecuación (2-3) puede escribirse:
tr
pkr
rr ∂
∂=
∂
∂
∂
∂







 ρφ
µ
ρ1
( )
estocon,
t∂
∂
=
∂
∂ ρ
φ
φρ
t
(2-3a)

29. 29
y considerando y constantes
Ecuación de difusividad en términos de
De la ecuación (2-5)
k µ
( )sc
p-pc
e
sc
ρρ=
(2-7)
















∂
∂
=
∂
∂
+
∂
∂
tk
c
rr
1
r
t
2
2
ρφµρρ
Sustituyendo
r
p
∂
∂ de la ec. (2-5)
rcr
p
∂
∂=
∂
∂ ρ
ρ
1
(2-5)
(2-6)
ρ

30. 30
Obtenemos:
Suponiendo que los gradientes de presión
son pequeños
t
p
k
tc
r
p
c
r
p
r
1
r
p 2
2
2
∂
∂
=
∂
∂
+
∂
∂
+
∂
∂







 φµ
Pongamos la ec. (2.3a) en función de
( )
t
sce
sc
pp
t ∂
∂−
=
∂
∂ p
cρ
ρ
p
0
(2-9)
0
r
p
2
≈
∂
∂








r
p
∂
∂
(2-8)

31. 31
y la ec. (2.9) puede escribirse
a esta ecuación linearizada se conoce como ecuación de
difusividad puede resolverse, para determinadas
condiciones de contorno e iniciales mediante métodos
analíticos.
















∂
∂
=
∂
∂
+
∂
∂
t
p
k
tc
r
p
r
1
r
p
2
2 φµ (2.10)
k
tcφµ Inverso del coeficiente de difusividad
hidráulica.

32. 32
Las suposiciones inherentes a la ec. (2.9) son:
•Flujo radial en el pozo, el cual esta produciendo a través de
toda la formación
•Medio poroso homogéneo e isotrópico
•Espesor uniforme
∀φ y K constantes (independientes de la presión)
•Fluido de compresibilidad pequeña y constante
•Viscosidad constante
•Gradientes de presión pequeños
•Efectos gravitacionales y térmicos despreciables
•Flujo monofásico

33. 33
ANALISIS DIMENSIONAL
La importancia de este análisis es que simplifica
los modelos del yacimiento involucrando
parámetros (como k) de tal manera que se reduce
el numero de incógnitas.
La ventaja adicional es que las soluciones son
independientes del sistema de unidades
empleado.
Se asume que K, µ, φ, B y h son constantes.

34. 34
ANALISIS DIMENSIONAL
En unidades de campo
En unidades consistentes
k = permeabilidad (md)
h = espesor (feet)
pi = Presión inicial del yacimiento (psi)
pwf = Presión de fondo fluyendo (psi)
q = Tasa de producción (STB/d)
B = factor volumétrico de formación (res vol/std vol)
µ = viscosidad(cp)

35. 35
ANALISIS DIMENSIONAL
En unidades de campo
En unidades consistentes
t = tiempo (horas)
φ = porosidad
ct = compresibilidad total del sistema (/psi)
rw = radio del pozo (ft)

36. 36
ANALISIS DIMENSIONAL
En unidades de campo
A= área del yacimiento = πre
2
re = radio del yacimiento (ft)

37. 37
EFECTO SKIN

38. 38
EFECTO SKIN
El radio efectivo, es el radio más pequeño que el
pozo aparenta tener debido a la reducción en el
flujo causada por el efecto de daño.

39. 39
EFECTO SKIN
EJEMPLO 2.1

40. 40
EFICIENCIA DE FLUJO

41. 41
ALMACENAMIENTO
Aunque el pozo puede producir a tasa constante
en la cabeza del pozo, el flujo en el wellbore
desde el yacimiento puede no ser constante.
Este efecto es debido al almacenamiento.
El almacenamiento puede ser causado
principalmente por:
•Expansión del fluido
•Cambios en el nivel del líquido

42. 42
Expansión del fluido
Consideremos un PDD. Cuando el pozo se abre
al flujo, la presión en el wb cae. Esta caída causa
una expansión del fluido en el wb y por lo tanto la
primera producción no es proveniente del
yacimiento sino del fluido que está almacenado
en el wb.
A medida que el fluido se expande, el wb se
desocupa hasta que no puede fluir más y el flujo
será netamente del yacimiento.
Por lo tanto es el wb quien proporciona la mayor
cantidad de fluido durante este periodo.

43. 43
Cambio en el nivel de líquido
Consideremos un PDD. Cuando el pozo se
abre al flujo, la reducción en la presión
causa que el nivel de líquido en el anular
disminuya. El fluido del anular se mezcla
con el proveniente del yacimiento.
El nivel de líquido del anular es
generalmente capaz de suministrar mucho
mas fluido que el proveniente por
expansión, por lo tanto los efectos del
almacenamiento son usualmente mucho
mas importantes en un completamiento
como el mostrado.

44. 44
COEFICIENTE DE
ALMACENAMIENTO
Este coeficiente (C) se usa para cuantificar el efecto
del almacenamiento.
C, es el volumen de fluido que el wb produce debido a
una caída de presión.

45. 45
COEFICIENTE DE
ALMACENAMIENTO

46. 46
COEFICIENTE DE
ALMACENAMIENTO

47. 47
COEFICIENTE DE
ALMACENAMIENTO
El valor del coeficiente de almacenamiento pude ser
calculado a partir de:
Para el caso de expansión de fluidos.
Donde cw es la compresibilidad del fluido y Vw es el
volumen del wellbore
Para el caso del nivel del anular
disminuyendo.
Donde Aw es el área seccional del wb y ρ es la
densidad del fluido.
EJEMPLO 2.2

48. 48
COEFICIENTE DE
ALMACENAMIENTOEl almacenamiento es la principal fuente de ruido en la
interpretación de pruebas ya que disfraza la respuesta
del yacimiento. Para vencer este problema es
conveniente medir las tasas de flujo en fondo.
Del balance de materia, la presión en el wb es
directamente proporcional al tiempo dominado por el
almacenamiento.
EJEMPLO 2.3
Una gráfica log-log de presión vs tiempo, proporciona
una línea recta característica de pendiente unitaria.

49. 49
COEFICIENTE DE
ALMACENAMIENTO

50. 50
COEFICIENTE DE
ALMACENAMIENTO
La línea de pendiente unitaria continua hasta un tiempo
dado por la siguiente ecuación:
Sin embargo, el efecto del almacenamiento no finaliza
a este tiempo, hay un periodo (generalmente uno y
medio ciclos logarítmicos) durante el cual existe una
transición entre la respuesta del wellbore y la respuesta
del yacimiento.
Por lo tanto la respuesta del yacimiento no empezará
hasta:
EJEMPLO 2.3

51. 51
SOLUCIONES PARA FLUJO
RADIAL DE UN FLUIDO DE
COMPRESIBILIDAD PEQUEÑA
Y CONSTANTE

52. 52
Fig. 2.2- Diagrama esquemático de un pozo en un yacimiento radial
mostrando los diferentes tipos de condiciones de contorno, para
tasa de flujo constante.
wr
h
∞→→ rcuandopp i
Caso de yacimiento infinito
Caso de yacimiento con
presión constante en el
limite exterior
ei
rrapp =→
w
r
1
kh2
qp
π
µ
=
∂
∂








wrr Caso de yacimiento
circular limitado
0=








∂
∂
err
p
q = constante
er

53. 53
I. Pozo produciendo a tasa de flujo constante
en un yacimiento infinito.
Condición inicial
El yacimiento se supone a una presión, pi , para t = 0
La solución se presenta en la Fig. 1
Pozo
(Condición contorno interior)
rw
Tasa de flujo constante
Limite exterior
(Condición contorno exterior)
INFINITO

54. 54
La solución a la ecuación de difusividad, para este caso
es:
( )




















−−−=
4kt
t
c
i
E
2
1
kh2
q
ptr,p i
2rφµ
π
µ
( )




















−−−=
0.00105kt
t
c
i
E
2
1
kh
141.2qB
ptr,p i
2rφµµ
La cual es conocida como SOLUCION DE LA LINEA
FUENTE


















−−=
D
4t
2
D
r
i
E
2
1
D
p
( )




















−+=
kt
t
c
i
E
kh
70.6qB
ptr,p i
2948 rφµµ

55. 55
Esta ecuación es válida para:
( )




















−+=
kt
t
c
i
E
kh
70.6qB
ptr,p i
2948 rφµµ
k
rc
t
k
rc etwt
22
948
φµφµ
≤≤5
10*3.79
Se usa para calcular presiones más allá de la zona alterada.

56. 56
Si X ≤0.01 entonces :
( ) ( )
5772.0
1
ln
)781.1ln(
ln
−





=
−=
−≅−
x
x
xx γiE-
25≥
2
D
r
D
t
01.0
2948
≤
kt
r
t
cφµ

57. 57
( )












−








+= Swr
2
21688
ln
kt
t
c
kh
70.6qB
ptr,p i
φµµ
Se usa para calcular presiones en la cara de la formación
de un pozo con una zona alterada. (para r = rw)
Ejemplo 1.1 Lee

58. 58
pD
Figura 1.
25

59. 59
Para tD/rD > 25, la solución de la integral exponencial
para rD = 1, puede ser aproximada por:
Al graficar la caída de presión vs log t se observa una
línea recta con pendiente

60. 60
El factor de daño puede ser obtenido a partir de la
diferencia entre pi y el intercepto de la línea recta.
Usualmente se emplea la siguiente ecuación:
El valor de P1hr debe ser tomado de la línea recta o la
extrapolación de la misma.

61. 61
Solución de un pozo de radio finito en un yacimiento
infinito.
Propiedades del gráfico (solución) de como función
de (ver Fig. 1)
es la localización donde se requiere la solución,
presiones adimensionales, generadas por el pozo activo.
La solución de la Línea Fuente (SLF) se considera de
radio infinitesimal, esto es:
D
p
2
DD
/rt
D
r
w
r ∞=⇒ D
r0,
1.
2.

62. 62
Las soluciones tienden a la SLF; luego
para usar la SLF para cualquier valor de
Todas las soluciones, para cualquier valor tienden
a la SLF para
Por lo tanto usar la solución de la línea fuente (SLF)
para cualquier localización , para
3.
4.
kh2
q
rr
pr0rlim
w
w
π
µ=
∂
∂
→ 







(en unidades
consistentes)
La condición de contorno en el pozo SLF es:
5.
20rD
≥
20rD
≥ 2
DD
/rt
D
r
25/rt 2
DD
≥
25/rt 2
DD
≥D
r

63. 63
6.
7.
Para valores de la SLF tiene una
aproximación logarítmica:
Para un pozo a tiempos pequeños (segundos,
minutos), se cumple que .
En consecuencia en la localización pozo usar la
aproximación logarítmica a la SLF.
252
D
/r
D
t ≥










+= 0.80907
r
t
ln
2
1
p
D
D
D 2
252
D
r/
D
t ≥

64. 64
Para un pozo real (con efecto de llene y efecto de daño,
skin) utilizar una fórmula modificada para incluir el
efecto “skin”:
que puede ser usada para pozos sin efecto de llene ó
para pozos con efecto de llene ( y “skin”) después que
desaparezcan los efectos (el efecto de llene es
perecedero, transitorio). El efecto skin para un pozo
fluyendo siempre esta presente.
La forma dimensional es:
S0.80907
r
t
ln
2
1
p
2
D
D
D
++=










( )
























+−+= − S08723.3
2
wr
t
c
k
logtlog
hk
162.6qB
pp iwf
µφ
µ
8.
9.

65. 65
donde S viene dado por:
Estas dos ecuaciones se utilizan en el Análisis de
Pruebas de flujo (“ drawdown “)




















+−= 23.3
2
wt
1hora
i
rc
k
log
m
wf
p-p
1.151S
φµ

66. Dp
2
/ DD rt 66
Solución de la Línea Fuente

67. 67

68. 68
X 0 1 2 3 4 5 6 7 8 9
0,00 6,332 5,639 5,235 4,948 4,726 4,545 4,392 4,259 4,142
0,01 4,038 3,944 3,858 3,779 3,705 3,637 3,574 3,514 3,458 3,405
0,02 3,355 3,307 3,261 3,218 3,176 3,137 3,098 3,062 3,026 2,992
0,03 2,959 2,927 2,897 2,867 2,838 2,81 2,783 2,756 2,731 2,706
0,04 2,681 2,658 2,634 2,612 2,59 2,568 2,547 2,527 2,507 2,487
0,05 2,468 2,449 2,431 2,413 2,395 2,377 2,36 2,344 2,327 2,311
0,06 2,295 2,279 2,264 2,249 2,235 2,22 2,206 2,192 2,178 2,164
0,07 2,151 2,138 2,125 2,112 2,099 2,087 2,074 2,062 2,05 2,039
0,08 2,027 2,015 2,004 1,993 1,982 1,971 1,96 1,95 1,939 1,929
0,09 1,919 1,909 1,899 1,889 1,879 1,869 1,86 1,85 1,841 1,832
0,10 1,823 1,814 1,805 1,796 1,788 1,779 1,77 1,762 1,754 1,745
0,11 1,737 1,729 1,721 1,713 1,705 1,697 1,689 1,682 1,674 1,667
0,12 1,66 1,652 1,645 1,638 1,631 1,623 1,616 1,609 1,603 1,596
0,13 1,589 1,582 1,576 1,569 1,562 1,556 1,549 1,543 1,537 1,53
0,14 1,524 1,518 1,512 1,506 1,5 1,494 1,488 1,482 1,476 1,47
0,15 1,464 1,459 1,453 1,447 1,442 1,436 1,431 1,425 1,42 1,415
0,16 1,409 1,404 1,399 1,393 1,388 1,383 1,378 1,373 1,368 1,363
0,17 1,358 1,353 1,348 1,343 1,338 1,333 1,329 1,324 1,319 1,314
0,18 1,31 1,305 1,301 1,296 1,291 1,287 1,282 1,278 1,274 1,269
0,19 1,265 1,261 1,256 1,252 1,248 1,243 1,239 1,235 1,231 1,227
0,20 1,223 1,219 1,215 1,21 1,206 1,202 1,198 1,195 1,191 1,187
0 +∞ 4,038 3,335 2,959 2,681 2,468 2,295 2,151 2,027 1,919
0,1 1,823 1,737 1,660 1,589 1,524 1,464 1,409 1,358 1,309 1,265
0,2 1,223 1,183 1,145 1,110 1,076 1,044 1,014 0,985 0,957 0,931
0,3 0,906 0,882 0,858 0,836 0,815 0,794 0,774 0,755 0,737 0,719
0,4 0,702 0,686 0,67 0,655 0,640 0,625 0,611 0,298 0,585 0,572
0,5 0,560 0,548 0,536 0,525 0,514 0,503 0,493 0,483 0,473 0,464
0,6 0,454 0,445 0,437 0,428 0,420 0,412 0,404 0,396 0,388 0,381
0,7 0,374 0,367 0,360 0,353 0,347 0,340 0,334 0,328 0,322 0,316
0,8 0,311 0,305 0,300 0,295 0,289 0,284 0,279 0,274 0,269 0,265
0,9 0,260 0,256 0,251 0,247 0,243 0,239 0,235 0,231 0,227 0,223
1,0 0,219 0,216 0,212 0,209 0,205 0,202 0,198 0,195 0,192 0,189
1,1 0,186 0,183 0,180 0,177 0,174 0,172 0,169 0,166 0,164 0,161
1,2 0,158 0,156 0,153 0,151 0,149 0,146 0,144 0,142 0,140 0,138
1,3 0,135 0,133 0,131 0,129 0,127 0,125 0,124 0,122 0,120 0,118
1,4 0,116 0,114 0,113 0,111 0,109 0,108 0,106 0,105 0,103 0,102
1,5 0,1000 0,0985 0,0971 0,0957 0,0943 0,0929 0,0915 0,0902 0,0889 0,0876
1,6 0,0863 0,0851 0,0838 0,0826 0,0814 0,0802 0,0791 0,0708 0,0768 0,0757
1,7 0,0747 0,0736 0,0725 0,0715 0,0705 0,0695 0,0685 0,0675 0,0666 0,0656
1,8 0,0647 0,0638 0,0629 0,062 0,0612 0,0603 0,0595 0,0586 0,0578 0,057
1,9 0,0562 0,0554 0,0546 0,0539 0,0531 0,0524 0,0517 0,051 0,0503 0,0496
2,0 0,0489 0,0482 0,0476 0,0469 0,0463 0,0456 0,045 0,0444 0,0438 0,0432
X 0 1 2 3 4 5 6 7 8 9
2 4.89x 10-2 4.26x 10-2 3.72x 10-2 3.25x 10-2 284x 10-2 2.49x 10-2 2.19x 10-2 1.92x 10-2 1.69x 10-2 1.48x 10-2
3 1.30x 10-2 1.15x 10-2 1.01x 10-2 8.94x 10-3 7.89x 10-3 6.87x 10-3 6.16x 10-3 5.45x 10-3 4.82x 10-3 4.27x 10-2
4 3.78x 10-3 3.35x 10-3 2.97x 10-3 2.54x 10-3 2.34x 10-3 2.07x 10-3 1.84x 10-3 1.64x 10-3 1.45x 10-3 1.29x 10-3
5 1.15x 10-3 1.02x 10-3 9.08x 10-4 8.09x 10-4 7.19x 10-4 6.41x 10-4 5.71x 10-4 5.09x 10-4 4.53x 10-4 4.04x 10-4
6 3.60x 10-4 3.21x 10-4 2.86x 10-4 2.55x 10-4 2.28x 10-4 2.03x 10-4 1.82x 10-4 1.62x 10-4 1.45x 10-4 1.29x 10-4
7 1.15x 10-4 1.03x 10-4 9.22x 10-5 8.24x 10-5 7.36x 10-5 6.58x 10-5 5.89x 10-5 5.26x 10-5 4.71x 10-5 4.21x 10-5
8 3.77x 10-5 3.37x 10-5 3.02x 10-5 2.70x 10-5 2.42x 10-5 2.16x 10-5 1.94x 10-5 1.73x 10-5 1.55x 10-5 1.39x 10-5
9 1.24x 10-5 1.11x 10-5 9.99x 10-6 8.95x 10-6 8.02x 10-6 7.18x 10-6 6.44x 10-6 5.77x 10-6 5.17x 10-6 4.64x 10-6
10 4.15x 10-6 3.73x 10-6 3.34x 10-6 3.00x 10-6 2.68x 10-6 2.41x 10-6 2.16x 10-6 1.94x 10-6 1.74x 10-6 1.56x 10-6
Ei (-X), 0.000 < 0.209, interval - 0.001
-Ei (-X), 0.00 < X > 2.09, interval = 0.01
2.0 < X < 10.9, interval = 0.1
Tabla 2.2. Valores de el exponente integral . –Ei(-x). Fuente Pet. Eng.(1956).
(Pág. 171-173)
Ei (-x), 0.000 < x < 0.209, interval =
0.001

69. 69
Este análisis está basado en la localización e
interpretación de la línea recta semilog (flujo
radial); sin embargo, es importante aclarar tener
en cuenta cuando finaliza el efecto del
almacenamiento para tener certeza del inicio de
la línea recta semilog.
ANALISIS SEMILOG

70. 70
1. Haga una grafica de ∆P vs t (log-log)
2. Determine el tiempo al cual finaliza la línea de
pendiente unitaria
3. Determine el tiempo 1 ½ ciclos después de que
finaliza la línea de pendiente unitaria. A este tiempo
se espera que empiece la línea recta semilog.
4. Haga una gráfica de p vs log t
5. Ubique la línea recta, empezando por el tiempo
determinado en el paso 3
6. Calcule la k, a partir de la pendiente
7. Estime el factor de daño, usando la presión a una
hora sobre la línea recta (no sobre los datos)
ANALISIS SEMILOG - Pasos
Ejemplo 2.6.1

71. 71
ANALISIS SEMILOG – Ejemplo 2.6.1
Bt (RB/STB) 1.21 rw (feet) 0.401
µo (cp) 0.92 h (feet) 23
ct (/psi) 8.7210-6 pi (psia) 6009
φ 0.21 q (STB/d) 2500

72. 72
ANALISIS SEMILOG – Ejemplo 2.6.1

73. 73
II. Yacimiento cerrado en el límite exterior,
q=constante en el pozo
Presenta tres (3) períodos de flujo:
(i) radial infinito (Aprox. Log a la SLF)
(ii) Transición
Depende de la posición del pozo en el área de drenaje:
más al centro menos duración del periodo de
transición.

74. t
hAc
qB
S
rC
A
kh
qB
pp
twA
iwf
φ
µ 2342.0
8686.0
2458.2
log
6.162
2
−





+





−=
S++=










2
wrAC
2.2458Aln
2
1
DA
t2
D
p π
74
o en unidades de campo (S ≠ 0)
(iii) Flujo semicontinuo
Modelado por:

75. t
hAc
qB
S
rC
A
kh
qB
pp
twA
iwf
φ
µ 2342.0
2
2458.2
ln
6.70
2
−





+





−=






+





−= S
rC
A
kh
qB
pp
wA
iwf 2
2458.2
ln
6.70
2
µ
75

76. 





+−





+−= S
r
r
t
rc
k
kh
qB
pp
w
e
et
iwf
4
3
ln
000528.02.141
2
φµ
µ






+−





−= S
r
r
kh
qB
pp
w
e
iwf
4
3
ln
2.141 µ
76
Si el área es circular:

77. 77
COMPORTAMIENTO DE P DEBIDO A LOS LIMITES

78. 78
Presiónadimensionalenelpozo,pD
Figura 2.6. Diagrama esquemático de Presión adimensional en el pozo, como función de Tiempo adimensional para
sistemas pozo-yacimiento radiales
tD

79. 79
Figura 2.9. Factores de forma y comienzo de flujo semicontinuo para diferentes sistemas pozo- yacimiento.

80. 80
III.Yacimiento a presión constante en el
límite exterior, pozo produciendo a tasa
de flujo constante.
Se presentan tres (3) períodos de flujo
(i) Flujo radial infinito moderado por la aprox.
Logarítmica a la SLF.
(ii) Transición.
(iii) Flujo continuo a tiempos de flujo grandes.
Modelado por:
DeD
rlnp =
wr
er
ln
kh
141.2qB
-
wf
p
µ
ip=

81. 81