Este documento presenta tres ejercicios sobre la aplicación de derivadas en problemas relacionados con las carreras de tecnologías geoespaciales y biotecnología. Inicialmente, se proporciona una fundamentación teórica sobre conceptos como derivadas, monotonía de funciones, máximos y mínimos, y concavidad. Luego, los ejercicios resuelven problemas de optimización utilizando derivadas para determinar las dimensiones óptimas de un depósito, el área máxima de un terreno y el volumen máximo de un cilind

1. Universidad de las Fuerzas Armadas, Av. General
Rumiñahui s/n
Sangolquı́-Ecuador
DEPARTAMENTO DE CIENCIAS EXACTAS
CÁLCULO DIFERENCIAL E INTEGRAL
PARCIAL 2
TALLER Nro. 2
27 de julio de 2021
NOMBRES:
1.Cacoango Pomaquero Joel Alexander
2.Lara Peña Cynthia Nicole
3.Maigua Maisincho Jonathan Fabricio
4.Maisincho Palaguaray Wendy Nicole
NRC : 2824
TEMA : APLICACIONES DE LA DERIVADA EN LA CARRERA DE
TECNOLOGIAS GEOESPACIALES Y BIOTECNOLOGIA
Perı́odo: Mayo 2021 Septiembre 2021
1

2. Índice
1. Introduccion 3
2. Objetivo(s) 3
2.1. Objetivo General . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
2.2. Objetivos Especı́ficos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
3. Fundamentación Teórica 3
3.1. Derivada . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
3.2. Monotonı́a de la Función . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
3.3. Funciones en el intervalo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
3.3.1. Función creciente: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
3.3.2. Función decreciente: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
3.3.3. Función constante: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
3.4. Criterio de la primera derivada para determinar los máximos y los mı́nimos de una
función . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
3.5. Concavidad y Puntos de Inflexión: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
3.5.1. Concavidad hacia arriba: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
3.5.2. Concavidad hacia abajo: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
3.5.3. Puntos de Inflexión: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
3.6. Criterio de la segunda derivada para establecer los valores máximos ylos valores mı́ni-
mos de una función . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
3.7. APLICACIONES DE LA DERIVADA . . . . . . . . . . . . . . . . . . . . . . . . . . 7
3.7.1. Problemas De Optimizaciı́on: . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
4. Desarrollo 7
4.1. Ejercicio 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
4.1.1. Grafica de la Funcion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
4.2. Ejercicio 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
4.2.1. Grafica de la Funcion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
4.3. Ejercicio 3 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
4.3.1. Grafica de la Funcion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
5. Conclusiones 11
5.1. Bibliografia . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
6. Enlace a slideshare 12
2

3. 1. Introduccion
Se definirá a la derivada y a cada uno de sus elementos, también se conocerá cada una de las reglas
de derivación, ası́ como los tipos de derivadas que se encuentran en los distintos problemas matemáti-
cos. Y por último se abordaran algunas aplicaciones de la derivada para obtención de elementos, como
máximos y mı́nimos para el análisis de las funciones.
2. Objetivo(s)
2.1. Objetivo General
Aplicar y resolver ejercicios de derivación, maximización y minimización en problemas relacio-
nados a la carrera.
2.2. Objetivos Especı́ficos
Resolver derivadas, maximización y minimización a través de las formulas establecidas en la
clase.
Aplicar ejercicios de derivadas, maximización y minimización en la carrera para un mejor des-
empeño al momento de tratar con problemas relacionados en la vida profesional.
3. Fundamentación Teórica
3.1. Derivada
La derivada de la función f(x) en el punto x = a es el valor del lı́mite, si existe, de un cociente
diferencial cuando el incremento de la variable independiente, x, tiende a cero, (Marta, 2021):
f,
(a) = L
f,
(a) = lim
x→a
∆f
∆x
f,
(a) = lim
x→a
f (x) − f(a)
x − a
f,
(a) = lim
h→0
f (a + h) − f(a)
h
Gráficamente, el cociente obtenido corresponde a la pendiente de la recta tangente en el
punto(a, f(a)) , recordando que la pendiente de una recta corresponde al cociente de la diferencia de
la variable dependiente con respecto a la variable independiente: m = Y1−Y0
X1−X0
Figura 1: Interpretación Geométrica de la Derivada
3.2. Monotonı́a de la Función
La primera derivada de una función proporciona información sobre la monotonı́a para determinar
cuándo una función es creciente o decreciente.
Consiste en determinar las caracterı́sticas de una función y el comportamiento de su gráfica a lo largo
de todo su dominio.
3

4. 3.3. Funciones en el intervalo
3.3.1. Función creciente:
Si Œ(a) < Œ(b) siempre que a < b
Figura 2: Creciente de una Función
3.3.2. Función decreciente:
Si Œ(a) > Œ(b) siempre que a > b
Figura 3: Decreciente de una Función
3.3.3. Función constante:
Si Œ(a) = Œ(b) siempre que a = b
Figura 4: Constante de una Función
3.4. Criterio de la primera derivada para determinar los máximos y los
mı́nimos de una función
En el siguiente teorema se establece cómo determinar los valores máximos y los valores mı́nimos
de una función, al estudiar los intervalos en que crece o decrece la función.
Donde:
Sea f una función continua en un intervalo cerrado [a,b] , que es derivable en todo punto del intervalo
abierto ]a,b[.
Sea c en [a,b] tal que f‘ (c) = 0 o que f‘ (c) no existe.
4

5. 3.1. Si f´(x) es positiva para todo x < c, , y negativa para todo x > c, entonces f(c) es un valor
máximo relativo de f(x) .
3.1. Si f´(x) es negativa para toda x < c, y positiva para toda x > c , entonces f(c) es un mı́nimo
relativo de f(x) .
3.1. Si f´(x) es positiva para todo x < c, y también lo es para todo x > c ; o si f´(x) es negativa
para todo x < c y a su vez para todo x > c , entonces f(c) no es un valor máximo relativo ni
un valor mı́nimo relativo de f(x) .
Las situaciones enunciadas en los literales a, b y c puede representarse gráficamente como:
Figura 5: Máximo relativo en x = c
Figura 6: Mı́nimo relativo en x = c
Figura 7: En x=c no hay ni mı́nimo ni máximo relativo
3.5. Concavidad y Puntos de Inflexión:
Como ya sabemos, si f´ (c) existe, entonces la gráfica de f tiene una recta tangente que pasa por el
punto P (c, f(c)) cuya pendiente es f´ (c). (Karelin Anatolyevich, 2009)
A continuación, se ilustran los tres casos que pueden ocurrir en la ubicación de la grafica con respecto
a la tangente:
Todo punto en el intervalo (a,b) de la gráfica esta por encima de la recta tangente.
La grafica está por debajo de la tangente en el intervalo (a,b).
La grafica que está por encima de la tangente y la otra por debajo.
5

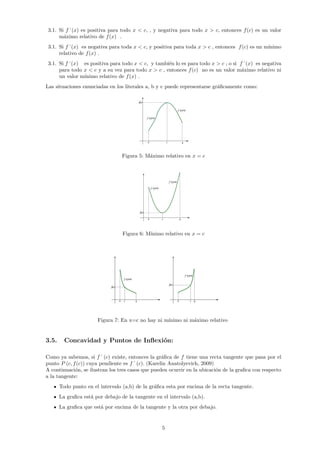
6. Figura 8: Por encima de la recta tangente
Figura 9: Por debajo de la recta tangente
3.5.1. Concavidad hacia arriba:
Sea f derivable en un número c, se dice que la gráfica de f es cóncava hacia arriba en el punto
P (c, f (c)) , si existe un intervalo abierto (a, b) que contenga a c, tal que en (a,b) la grafica de f esta
arriba de la recta tangente en P.
Si f´´ (c) > 0, la grafica de f es cóncava hacia arriba en P (c, f (c))
Figura 10: Cóncava hacia arriba
3.5.2. Concavidad hacia abajo:
Sea f derivable en un numero c, se dice que la gráfica de f es concava hacia abajo en el punto
P(c, f(c)) si existe en un intervalo abierto (a, b) que contenga a c, tal que en (a, b) la gráfica de f
esta bajo la recta tangente en P.
Si f´´ (c) < 0, la grafica de f es cóncava hacia abajo en P (c, f (c)) .
3.5.3. Puntos de Inflexión:
Un punto P(c.f(c)) en la grafica de f se denomina punto de inflexión si f´´ existe en un intervalo
abierto (a,b) que contiene a c y f´´ cambia de signo en c.
P es un punto de Inflexión:
3.6. Criterio de la segunda derivada para establecer los valores máximos
ylos valores mı́nimos de una función
Además de proporcionar información sobre la concavidad de la gráfica de una función, la segunda
derivada permite establecer si un punto crı́tico es un valor máximo o un valor mı́nimo. (Leon, s.f.)
Si f´´ (x) está definida para x ∈ ]a, b[ donde ]a, b[ ⊂ D y si f´(x0) = 0 con x0 ∈ ]a, b[ entonces:
f(x0) es un valor máximo relativo de f si se cumple que f´´(x0) < 0
f(x0) es un valor mı́nimo relativo de f si se cumple que f´´(x0) > 0
6

7. Figura 11: Cóncava hacia abajo
Figura 12: Punto P es un punto de inflexión
3.7. APLICACIONES DE LA DERIVADA
3.7.1. Problemas De Optimizaciı́on:
Los resultados expuestos en la sección anterior permiten hallar los valores máximos y mı́nimos de una
función.
Si se aplican a problemas en los cuales están involucradas funciones conocidas, es posible obtener los
valores óptimos de ellas.
Una estrategia adecuada para la resolución de este tipo de problemas es la siguiente:
3.1. Identificar la función a optimizar.
3.2. Si la función del punto anterior posee dos variables, es necesario identificar una relación adicional
entre ellas para dejar una en términos de la otra y sustituirla en la función de optimizar.
3.3. Derivar la funcion a optimizar para hallar los puntos crı́ticos.
3.4. Utilizar el criterio de la segunda derivada, o bien, el de la n-ésima deriva para determinar los
máximos o mı́nimos.
4. Desarrollo
4.1. Ejercicio 1
Usted es contratado para desarrollar un programa que muestre las dimensiones de un depósito
abierto superiormente en forma de prisma recto de base cuadrada como datos a probar nos dan una
base de 50 m3
de volumen, cuáles son las dimensiones para que el deposito tenga una superficie
mı́nima.
Figura 13: grafica ilustracion ejercicio 1
7

8. Datos:
V = x2
y
V = 50m3
y =
50
x2
La superfice sera la suma de cuatro caras laterales iguales y la base cuadrada.
S = 4xy + x2
f(x) = 4x
50
x2
+ x2
=
200
x
+ x2
Primera derivada
f0
(x) = −
200
x2 + 2x
f0
(x) = 0 ⇒ −
200
x2
+ 2x = 0 ⇒ 2x =
200
x2 ⇒ x3
= 100
⇒ x =
3
√
100
Segunda Derivada
f00
(x) =
400
x3
+ 2
f00
(
3
√
100) =
400
( 3
√
100)3
+ 2 =
400
100
+ 2 = 6 > 0
Punto minimo
⇒ x =
3
√
100
f(x) =
200
x
+ x2
f(
3
√
100) =
200
3
√
100
+
3
√
100
2
⇒ y =
300
3
√
100
Por lo tanto las dimenciones serian:
⇒ x =
3
√
100
⇒ y =
50
3
√
100
2
=
50( 3
√
100)
100
⇒ y =
3
√
100
2
cm ⇒ x =
3
√
100cm
4.1.1. Grafica de la Funcion
Figura 14: Grafica de la función
8

9. 4.2. Ejercicio 2
La suma de tres posiciones georreferenciales dadas en kilómetros a través de individuos es 60km.
El primer individuo más la doble distancia del segundo individuo m as la triple distancia del tercero
suman 120km. Hallar la distancia total que verifican estas condiciones y cuyo producto es máximo.
Datos
Sean ”x”,2
”, ”z”
x + y + z = 60
x + 2y + 3z = 120
(e2 − e1) : y + 2z = 60 ⇒ y = 60 − 2z
(2e1 − e2) : x − z = 0 ⇒ y = x = z
El producto es:
P = x.y.z = z(60 − 2z).z
La funcion a maximizar es
f(z) = z(60 − 2z)z
⇒ f(z) = 60z2
− 2z3
Primera derivada:
f0
(z) = 120z − 6z2
f0
(z) = 0 ⇒ 120z − 6z2
= 0 ⇒ 6z(20 − z) = 0
⇒
z = 0
z = 20
(1)
Segunda Derivada:
f00
(z) = 120 − 12z
f00
(0) = 120 − 12(0) = 120 0; z = 0 es un minimo
f00
(z) = 120 − 12z
f00
(0) = 120 − 12(20) = −120 0; z = 20 es un maximo
y = 60 − 2(20) = 60 − 40 = 20
x = z = 20
Portanto los tres numeros osn iguales a 20
4.2.1. Grafica de la Funcion
Figura 15: Grafica de la función
9

10. 4.3. Ejercicio 3
Se necita desarrollar un algoritmo para determinar la mayor área que puede encerrar un triángulo
rectángulo cuyo lado mayor mida 1 metro.
Datos
x2
+ y2
= 1 ⇒ y =
p
1 − x2
El area es:
S =
1
2
xy =
1
2
x
p
1 − x2
La funcion a maximizar es:
f(x) =
x
2
p
1 − x2
Primera derivada:
f0
(x) =
1
2
p
1 − x2 +
1
2
x
−2x
2
√
1 − x2
=
1
2
p
1 − x2 −
1
2
.
x2
√
1 − x2
=
⇒=
1
2
1 − x2
− x2
√
1 − x2
f0
(x) =
1 − 2x2
2
√
1 − x2
f0
(x) = 0 ⇒
1 − 2x2
2
√
1 − x2
= 0 ⇒
⇒ 1 − 2x2
= 0 ⇒ x = + −
r
1
2
= + −
√
2
2
Segunda derivada:
f00
(x) =
1
2
−4x.
√
1 − x2 − (1 − 2x2
)
−2x
2
√
1 − x2
1 − x2
=
1
2
−4x.(1 − x2
)
√
1 − x2
+
x.(1 − 2x2
)
√
1 − x2
1 − x2
=
1
2
.
−4x.(1 − x2
) + x(1 − 2x2
)
(1 − x2)
√
1 − x2
=
1
2
.
2x3
− 3x
(1 − x2)
√
1 − x2
f(
√
2
2
) =
1
2
.
2(
√
2
2
)3
− 3(
√
2
2
)
(1 − (
√
2
2
)2).
r
1 − (
√
2
2
)2
=
1
2
.
2.
2
√
2
8
−
3
√
2
2
(1 −
2
4
).
r
1 −
2
4
=
1
2
.
−
√
2
1
2
r
1
2
0
10

11. Maximo en:
x =
√
2
2
Los catetos del triangulo son:
x =
√
2
2
y =
p
1 − x2 =
s
1 − (
√
2
2
)2 =
r
1 −
2
4
y =
√
2
2
Es un triangulo isosceles
4.3.1. Grafica de la Funcion
Figura 16: Grafica de la función
5. Conclusiones
Permite identificar el crecimiento máximo y mı́nimo de una función.
La Investigación y ejercicios ejecutados nos ayudan a una mejor comprensión para una mejor
resolución de los problemas solicitados en la carrera.
Una función al momento de derivarla se conoce que gráficamente es la tangente de la recta de la
función original de igual manera se conoce que una función está compuesta por una monotonı́a
la cual se divide en dos partes que son Creciente y Decreciente los cuales permiten determinar el
comportamiento d ella función en su Dominio, también contiene los puntos máximos y mı́nimos
los cuales son los que delimitan la gráfica de la función, también está la concavidad que está
dividida en 2 las culés son la concavidad hacia arriba y la concavidad hacia abajo y los puntos
de inflexión el cual sucede cuando una gráfica invierte su forma, de igual manera toda función
derivada tiene su segunda derivada la cual nos ayuda para el cálculo de la optimización.
11

12. 5.1. Bibliografia
Referencias
[1] Cimanet A(s.f), Concepto de Derivada url: http://cimanet.uoc.edu/cursMates0.html
[2] Marta(2021), Concepto de Derivada de una funcion en un punto. url:
https://www.superprof.es/apuntes/escolar/matematicas/calculo/derivadas/concepto-de-
derivada.html,2021
[3] Karelin.A(2009), Estudio sobre la recta tangente en puntos de inflexion
[4] Leon.M(s.f), Definicion de la derivada
6. Enlace a slideshare
12