Este informe trata sobre la optimización (máximos y mínimos) utilizando los criterios de la primera y segunda derivada. El documento define conceptos como derivada, máximos y mínimos, e incluye ejemplos de problemas de optimización resueltos aplicando los criterios de la primera y segunda derivada.

1. FACULTAD DE INGENIERIA
INFORME DE OPTIMIZACION (MINIMOS Y MAXIMOS).
INFORME MATENATICA II.
AUTOR(ES):
 CHACON CURO FELIPE.
 JUARES RODRIGUEZ CARLOS.
 MACHADO PERALTA CARLOS.
 OLIVA JIMENEZ CARLOS.
 PAREDES NARVÁEZ, KALY.
ASESOR:
 Ing. EVELIO VIGO LECCA.
Trujillo-Perú
2016

2. Matemática II
2
ÌNDICE
ÍNDICE.
I. INTRODUCCIÓN…………………………………………………………………..…3
II. RESUMEN……………………………………………………………………………..4
III. OBJETIVOS…………………………………………………………………….……..5
Objetivo general
Objetivos específicos
IV. MARCO TEORICO……………………………………………………………………5
Optimizacion.
Derivada.
Maximos y minomos.
criterios de la primera derivada.
criterios de la segunda derivada.
ejercicios aplicativos.
V. CONCLUSIONES…………………………………………………………………….22
VI. REFERENCIAS BIBLIOGRÁFICAS………………………………………………..23
ANEXOS………………………………………………………………………………….........24

3. Matemática II
3
I. INTRODUCCIÓN.
El trabajo está basado, en la optimización (máximos y mínimos) y haciendo uso de los
criterios de la primera derivada y segunda derivada, que se basa en muchos problemas
que se nos presentan cotidianamente y profesionalmente.
E l problema fundamental asociado al uso de funciones para modelar problemas
económicos consiste en calcular los valores de la variable independiente para los cuales
la función toma un valor que se puede considerar máximo o mínimo de la función en
cierto contexto.
Se resuelve este problema de optimización con el uso de la derivada de la función. En
esta unidad se desarrollan criterios basados en la primera y segunda derivada de la
función para identificar los valores óptimos de la función. Además, se estudian otros
criterios que permiten determinar los intervalos donde la función crece, o decrece, su tipo
de concavidad y los puntos donde la concavidad cambia, aspectos que son importantes
para conocer el comportamiento de la función en su dominio.

4. Matemática II
4
II. RESUMEN.
La derivada es el resultado de un límite y representa la pendiente de la recta tangente a
la gráfica de la función en un punto.
Los máximos y mínimos de una función conocidos como extremos de una función, son
los valores más grandes (máximos) o más pequeños (mínimos)
El criterio de la primera derivada es Obtener la primera derivada, Igualar la primera
derivada a cero y resolver la ecuación.
El valor o valores obtenidos para la variable, son donde pudiera haber máximos o mínimos
en la función.
El criterios de la segunda derivada. Este método es más utilizado que el anterior, aunque
no siempre es más sencillo. Se basa en que en un máximo relativo, la concavidad de una
curva es hacia abajo y en consecuencia, su derivada será negativa; mientras que en un
punto mínimo relativo, la concavidad es hacia arriba y la segunda derivada es positiva.
Un punto de inflexión, en una función matemática, es un punto donde los valores de
una función continua x pasan de un tipo de concavidad a otra. La curva "atraviesa" la
tangente. Matemáticamente la derivada segunda de la función f en el punto de
inflexión es cero, o no existe.
El área es un concepto métrico que permite asignar una medida a la extensión de una
superficie, expresada en matemáticas unidades de medida denominadas unidades de
superficie. El área es un concepto métrico que requiere que el espacio donde se define o
especifique una medida.
La 'velocidad media' o velocidad es el cambio de posición en el tiempo.
El cálculo de velocidades relativas en mecánica clásica es aditivo y encaja con la intuición
común sobre velocidades; de esta propiedad de la aditividad surge el método de la
velocidad relativa.
La velocidad angular no es propiamente una velocidad en el sentido anteriormente definido
sino que es una medida de la rapidez con la que ocurre un movimiento de rotación.

5. Matemática II
5
OBJETIVOS
Objetivos generales
Resolver problemas de optimización, vinculados a la especialidad y cualquier otro caso
aplicativo haciendo uso de la derivada.
Objetivo específico.
Determinar los intervalos de una función, haciendo uso de los criterios de la primera y
segunda derivada.
Aplicar los criterios de la derivada correctamente, en la resolución de problemas.
III. MARCO TEORICO
a) OPTIMIZACIÓN
La optimización intenta aportar respuestas a un tipo general de problemas que consiste
en seleccionar el mejor entre un conjunto de elementos.
b) DERIVADAS
La derivada es el resultado de un límite y representa la pendiente de la recta tangente a
la gráfica de la función en un punto.
La definición de derivada es la siguiente:

6. Matemática II
6
La recta tangente.
La noción de Euclides de una tangente, como una recta que toca a una curva en un solo
punto es totalmente correcta para circunferencias; pero completamente insatisfactoria
para otras curvas (figura 2). La idea de una tangente, en P a una curva como la recta que
mejor se aproxima a la curva cerca de P es bastante mejor, pero aún muy vaga para la
precisión matemática. El concepto de límite proporciona una manera de obtener una
mejor descripción.
Encuentre la pendiente de la recta tangente a la curva f (x) = x2
en el punto (2, 4).
SOLUCIÓN.
La recta cuya pendiente estamos buscando se muestra en la figura 5. Es claro que tiene
una pendiente positiva grande.

7. Matemática II
7
MXIMOS Y MÍNIMOS
Loa máximos y mínimos de una función conocidos como extremos de una función , son
los valores más grandes (máximos) o más pequeños (mínimos) que toma una función en
un punto situado ya sea dentro de una región en particular de la curva o en el dominio de
la función en su totalidad.
Con frecuencia en la vida, nos enfrentamos con el problema de encontrar la mejor
manera de hacer algo. Por ejemplo, un granjero necesita elegir la mezcla de cultivos
Que sea la más apropiada para producir la mayor ganancia. Un médico desea
seleccionar la menor dosis de una droga que curará cierta enfermedad. A un fabricante le
Gustaría minimizar el costo de distribución de sus productos. Algunas veces, un problema
de este tipo puede formularse de modo que implique maximizar o minimizar una función
en un conjunto específico. Si es así, los métodos de cálculo proporcionan una
herramienta poderosa para resolver el problema.
TEOREMAS DE VALORES EXTREMOS
Si “f” es continua en un intervalo cerrado I= [a, b] entonces “f” tiene un valor máximo
absoluto “M” y un valor mínimo absoluto “m” en [a, b].

8. Matemática II
8
PUNTO CRÍTICO DE UNA FUNCIÓN
Para resolver todos los puntos críticos de una función pilonó mica se debe resolver:
f´(x) = 0
Ejemplo:
F(x)= 3x4
-16x3
+18x2
f¨(x)= 12x3
-48x2
+36x
12x3
-48x2
+36x = 0
12𝑥3
12
−
48𝑥2
12
+
36𝑥
12
= 0
X 3
-4x2
+3x = 0
X(x2
-4x+3x)=0
X(x-3) (x-1)
x=0 x=3 x=1

9. Matemática II
9
FUNCIONES CRECIENTES Y DECRECIENTES.
Si f es continua en un intervalo cerrado i= [a, b] y y derivable en el intervalo abieto (a, b).
 Si f´(x) >0 para todo x € (a, b), entonces f es creciente en [a, b]
 Si f´(x) <0 para todo x € (a, b), entonces f es decreciente en [a, b]
Ejemplo.
F(x)=x3
-12x-5
 Determine los puntos críticos de la función.
 Identificar los intervalos donde la función es creciente y decreciente.
f´(x)=3x2
-12
f´(x)=0
3x2
-12=0
3𝑥2
3
−
12
3
= 0
X2
-4=0
(x-2) (x+2)=0
X=-2 x=2

10. Matemática II
10
puntos críticos de la función.
f´ (-3)>0 “f” es creciente en el intervalo en (-∞, -2 ]
f´ (0) <0 “f” es decreciente en el intervalo en [-2, 2]
f´ (3)>0 “f” es creciente en el intervalo en [2,+∞)
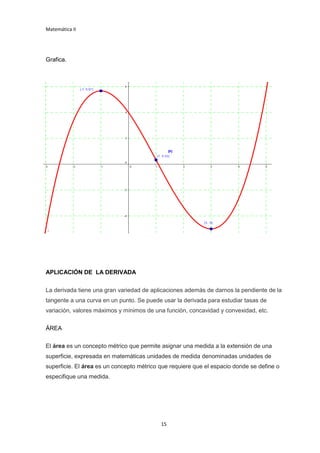
GRÁFICA
f (-2) = 11
f (2) = 21
f (0) = -5

11. Matemática II
11
CRITERIOS DE LA PRIMERA DERIVADA
 obtener la primera derivada.
 igualar la primera derivada a cero y resolver la ecuación.
 El valor o valores obtenidos para la variable, son donde pudiera haber máximos o
mínimos en la función.
· se asignan valores próximos (menores y mayores respectivamente) a la variable
independiente y se sustituyen en la derivada. Se observan los resultados; cuando estos
pasan de positivos a negativos, se trata de un punto máximo; si pasa de negativo a
positivo el punto crítico es mínimo.
Cuando existen dos o más resultados para la variable independiente, debe tener la
precaución de utilizar valores cercanos a cada uno y a la vez distante de los demás,
a fin de evitar errores al interpretar los resultados.
· sustituir en la función original (Y) el o los valores de la variable independiente (X) para
los cuales hubo cambio de signo. Cada una de las parejas de datos así obtenidas,
corresponde a las coordenadas de un punto crítico.
TEOREMA
Sea f(x) continua en [a, b] y diferenciable en (a, b), excepto posiblemente en el valor
crítico c.
 Si f '(x)>0 para a<x<c y f '(x) < 0 para c<x<b entonces f(c) es un máximo relativo.
 Si f '(x) <0 para a<x<c y f '(x)>0 para c<x<b entonces f(c) es un mínimo relativo.

12. Matemática II
12
EJEMPLO:
𝑓(𝑥) =
𝑥2
− 2𝑥 + 4
𝑥 − 2
 Haciendo uso de la primera derivada determiné los máximos locales y mínimos
locales.
Dominio R €X – {2}.
𝑓′(𝑥) =
(2𝑥 − 2)(𝑥 − 2) − (𝑥2
− 2𝑥 + 4)(1)
(𝑥 − 2)2
c
𝑓′(𝑥) =
2𝑥2
− 4𝑥 − 2𝑥 + 4 − 𝑥2
+ 2𝑥 − 4
(𝑥 − 2)2
𝑓′(𝑥) =
𝑥2
− 4𝑥
(𝑥 − 2)2
𝑓′(𝑥) =
𝑥(𝑥 − 4)
(𝑥 − 2)2
f´(x)=0
𝑓′(𝑥)
=
𝑥(𝑥 − 4)
(𝑥 − 2)2
= 0
X= 0 x= 4
puntos críticos de la función.
Nota: cundo x= 2 no es un punto crítico porque 4/0 no existe.
f´ (-1)>0 “f” es creciente en el intervalo en (-∞, 0 ]
f´ (1)<0 “f” es decreciente en el intervalo en [0, 2 )
f´ (3) <0 “f” es decreciente en el intervalo en (2, 4]
f´ (5)>0 “f” es creciente en el intervalo en [4,+∞)

13. Matemática II
13
GRÁFICA
f 4) = -2
f (0) = 6
CRITERIOS DE LA SEGUNDA DERIVADA
Este método es más utilizado que el anterior, aunque no siempre es más sencillo. Se
basa en que en un máximo relativo, la concavidad de una curva es hacia abajo y en
consecuencia, su derivada será negativa; mientras que en un punto mínimo relativo, la
concavidad es hacia arriba y la segunda derivada es positiva.
Este procedimiento consiste en:
calcular la primera y segunda derivadas
igualar la primera derivada a cero y resolver la ecuación.
sustituir las raíces (el valor o valores de X) de la primera derivada en la segunda
derivada.
Si el resultado es positivo, hay mínimo. Si la segunda derivada resulta negativa,
hay un máximo.
Si el resultado fuera cero, no se puede afirmar si hay o no un máximo o mínimo.
sustituir los valores de las raíces de la primera derivada en la función original, para
conocer las coordenadas de los puntos máximo y mínimo.
PUNTOS DE INFLECCIÓN.
Un punto de inflexión, en una función matemática, es un punto donde los valores de
una función continua x pasan de un tipo de concavidad a otra. La curva "atraviesa" la
tangente. Matemáticamente la derivada segunda de la función f en el punto de
inflexión es cero, o no existe.
- Igualar la segunda derivada con cero (0). (En este caso no hay punto de inflexión)

14. Matemática II
14
GRÁFICA:
- Sustituyes en la función original el punto crítico. (Hay casos en que son dos puntos
críticos).
- Sustituyes en la función original el punto de inflexión.
- Gráficas
EJEMPLO:
Puntos críticos.
Valores máximos y mínimos.
Punto de inflexión.
La gráfica de la función.
𝑓(𝑥) =
1𝑥3
3
− 𝑥2
− 3𝑥 + 4
𝑓′(𝑥) = 𝑥2
− 2𝑥 − 3
F’(x)=0
𝑥2
− 2𝑥 − 3 = 0
(x-3), (x+1) f’ (-1)= 17/3 Max.
X=3, x=-1 f’ (3) = -5 min.
𝑓′′(𝑥) = 𝑥2
− 2𝑥 − 3
𝑓′′(𝑥) = 2𝑥 − 2
F’’(x)=0
2x-2 = 0 2(x-1) = 0 x=1 punto crítico de inflexión.
PI= (c, f(c))
PI= (1, 1/3)

15. Matemática II
15
Grafica.
APLICACIÓN DE LA DERIVADA
La derivada tiene una gran variedad de aplicaciones además de darnos la pendiente de la
tangente a una curva en un punto. Se puede usar la derivada para estudiar tasas de
variación, valores máximos y mínimos de una función, concavidad y convexidad, etc.
ÁREA
El área es un concepto métrico que permite asignar una medida a la extensión de una
superficie, expresada en matemáticas unidades de medida denominadas unidades de
superficie. El área es un concepto métrico que requiere que el espacio donde se define o
especifique una medida.

16. Matemática II
16
RECTANGULO
Perímetro
La palabra perímetro Se refiere al contorno de una superficie o de una figura y a
la medida de ese contorno.
Área.
El área de una figura, es que el área es la que posibilita el conocimiento de su superficie interior.
PERÍMETRO Y ÁREA DEL RECTÁNGULO MATEMATICAMENTE.
PERÍMETRO
El rectángulo tiene los lados iguales dos a dos, por tanto:
P = 2· a + 2· b
ÁREA DEL RECTÁNGULO
El área de un rectángulo es el producto de la longitud de los lados.
A= a · b

17. Matemática II
17
PROBLEMA 1.
un granjero dispone de 100 metros de valla con los que desea construir un corral
rectangular de la maxima superficie posible.
X= Ancho
Y=Largo
AREA:
Amax=YX
PERIMETRO:
𝑷 = 𝑋 + 𝑌 + 𝑋 + 𝑌 𝑷 = 2𝑋 + 2𝑌 100 = 2𝑋 + 2𝑌 100 = 2(𝑋 + 𝑌) 50 = 𝑋 + 𝑌
𝟓𝟎 − 𝑿 = 𝒀
AREA MAXIMA:
Amax=YX 𝐴 = (50 − 𝑋)𝑋 𝑨 = 𝟓𝟎𝑿 − 𝑿2
PUNTOS CRITICOS DE LA FUNCION:
𝐴 = 50𝑋 − 𝑋2
Derivamos 𝐴 = 50 − 2𝑋 𝑿 = 𝟐𝟓

18. Matemática II
18
AMAX: XY
𝒀 = 𝟓𝟎 − 𝑿 𝑨 = (𝟓𝟎 − 𝑿)𝑿 𝑨 = (𝟓𝟎 − 𝟐𝟓)𝟐𝟓 𝑨 = (𝟐𝟓)(𝟐𝟓) 𝑨 = 𝟔𝟐𝟓𝑼2
PROBLEMA 2.
Velocidad media
La 'velocidad media' o velocidad es el cambio de posición en el tiempo. Se calcula
dividiendo el desplazamiento (Δr) entre el tiempo (Δt) empleado en efectuarlo:
 Esta es la definición de la velocidad media entendida como vector (ya que es el
resultado de dividir un vector entre un escalar).
Por otra parte, si se considera la distancia recorrida sobre la trayectoria en un
intervalo de tiempo dado, tenemos la velocidad media sobre la
trayectoria o rapidez media, la cual es una cantidad escalar. La expresión anterior
se escribe en la forma:
 La velocidad media sobre la trayectoria también se suele denominar «velocidad
media numérica» aunque esta última forma de llamarla no está exenta de
ambigüedades.
El módulo de la velocidad media (entendida como vector), en general, es diferente
al valor de la velocidad media sobre la trayectoria. Solo serán iguales si la
trayectoria es rectilínea y si el móvil solo avanza (en uno u otro sentido) sin
retroceder. Por ejemplo, si un objeto recorre una distancia de 10 metros en un
lapso de 3 segundos, el módulo de su velocidad media sobre la trayectoria es:

19. Matemática II
19
Velocidad relativa.
El cálculo de velocidades relativas en mecánica clásica es aditivo y encaja con la intuición
común sobre velocidades; de esta propiedad de la aditividad surge el método de la
velocidad relativa. La velocidad relativa entre dos observadores A y B es el valor de la
velocidad de un observador medida por el otro. Las velocidades relativas medidas por A y
B serán iguales en valor absoluto pero de signo contrario. Denotaremos al valor la
velocidad relativa de un observador B respecto a otro observador A como .
Dadas dos partículas A y B, cuyas velocidades medidas por un cierto observador son y ,
la velocidad relativa de B con respecto a A se denota como y viene dada por:
Naturalmente, la velocidad relativa de A con respecto a B se denota como y viene dada
por: de modo que las velocidades relativas y tienen el mismo módulo pero dirección
contraria. Aquí E es un sistema inercial de referencia, que puede ser la tierra.
Si pasamos Vbe del segundo miembro al primer miembro de la expresión anterior
obtenemos: Vae = Vab + Vbe, que nos da la manera de determinar vectorialmente la
velocidad de A, en relación a la tierra, cuando se conoce la velocidad de B (en relación a
la tierra) y la velocidad relativa de A en relación a B. Esta es una suma vectorial, como se
pude observar.
Velocidad angular
La velocidad angular no es propiamente una velocidad en el sentido anteriormente
definido sino que es una medida de la rapidez con la que ocurre un movimiento de
rotación. Aunque no es propiamente una velocidad una vez conocida la velocidad de un
punto de un sólido y la velocidad angular del sólido se puede determinar la velocidad
instantánea del resto de puntos del sólido.

20. Matemática II
20
Condición:
0 ≤ ϕ ≤ π/2
𝑑𝑅
𝑑ϕ
=
𝑣0
2
𝑠𝑒𝑛2ϕ
𝑔
=
(𝑣0
2
𝑠𝑒𝑛2ϕ)´(g) − (𝑣0
2
𝑠𝑒𝑛2ϕ)(g)´
𝑔2
=
(𝑣0
2
)´(𝑠𝑒𝑛2ϕ) + (𝑣0
2
)(𝑠𝑒𝑛2ϕ)´(g) − (𝑣0
2
𝑠𝑒𝑛2ϕ)
𝑔2
=
𝑣0
2
𝑠𝑒𝑛2ϕ + 𝑣0
2(𝑐𝑜𝑠2ϕ)(2)(g) − (𝑣0
2
𝑠𝑒𝑛2ϕ)
𝑔2
=
2𝑣0
2
𝑐𝑜𝑠2ϕ
𝑔
Igualamos a cero.
2𝑣0
2
𝑐𝑜𝑠2ϕ
𝑔
= 0
2𝑣0
2
𝑐𝑜𝑠2ϕ = 0
𝑐𝑜𝑠2ϕ = 0
2ϕ = arcocos(0)
ϕ =
π
2⁄
2
=
𝜋
4
= 90

21. Matemática II
21
Aplicamos la segunda derivada.
𝑑2
𝑅
𝑑ϕ2
=
2𝑣0
2
𝑐𝑜𝑠2ϕ
𝑔
=
(2𝑣0
2
𝑐𝑜𝑠2ϕ)´(g) − (2𝑣0
2
𝑐𝑜𝑠2ϕ)(g)´
𝑔2
=
(2𝑣0
2
)´(𝑐𝑜𝑠2ϕ) + (2𝑣0
2
)(𝑐𝑜𝑠2ϕ)´(g) − (2𝑣0
2
𝑐𝑜𝑠2ϕ)
𝑔2
=
2𝑣0
2
𝑐𝑜𝑠2ϕ + 2𝑣0
2
(−𝑠𝑒𝑛2ϕ)(2)(g) − (2𝑣0
2
𝑐𝑜𝑠2ϕ)
𝑔2
=
−4𝑣0
2
𝑠𝑒𝑛2ϕ
𝑔
Sustituimos
−4𝑣0
2
𝑠𝑒𝑛2(𝜋 4⁄ )
𝑔
=
𝑑2 𝑅
𝑑ϕ2 =
−(4𝑣0
2
)
𝑔
< 0 𝑠𝑒𝑛2(𝜋 4⁄ ) = 1
Por lo tanto: en ϕ =𝜋 4 ∋ 𝑚𝑎𝑥𝑖𝑚𝑜⁄
Sustituimos en la función original:
𝑅(ϕ) =
𝑣0
2
𝑠𝑒𝑛2ϕ
𝑔
𝑅(ϕ) =
𝑣0
2
𝑔

22. Matemática II
22
IV. CONCLUSIONES.
Concluimos que la aplicación de la derivada podemos resolver diversos tipos de
problemas matemáticos como áreas, volúmenes ángulos, etc. y los que se presentan en
la vida cotidiana. Y por otra parte aplicando el primer criterio de la derivada determinamos
los puntos máximos y mínimos relativos de una función, y por el segundo criterio
podemos determinar la concavidad de una función, la derivada nos ayuda a determinar
los puntos críticos de una función.

23. Matemática II
23
V. REFERENCIAS BIBLIOGRÁFICAS.
 http://es.slideshare.net/search/slideshow?searchfrom=header&q=maximos+y+mini
mos
 http://es.slideshare.net/agascras/variacion-de-funciones-5995130?qid=e728f0f3-
69c1-4f40-abe5-94dc56a0f24a&v=&b=&from_search=3
 http://www.vadenumeros.es/primero/derivadas-maximos-y-minimos.htm
 http://latinoamerica.cengage.com

24. Matemática II
24
ANEXOS.