Este documento describe la metodología de Seis Sigma, incluyendo las fases de definición, medición, análisis, mejora y control. Se enfoca en la fase de análisis, describiendo herramientas como el Análisis de Modo y Efecto de Falla y estudios de repetibilidad y reproducibilidad. Explica cómo realizar estos estudios para evaluar la consistencia de un sistema de medición y mejorar la definición de medidas cuando se identifican inconsistencias.

1. UIA
Curso de Seis Sigma
Transaccional para Black Belts
Módulo II
Primitivo Reyes Aguilar / Noviembre 2004
1

2. Contenido - Módulo II
1. Introducción
2. Despliegue de Seis Sigma en la empresa
3. Gestión de procesos en la empresa
4. Gestión de proyectos y liderazgo
5. Fase de Definición
6. Fase de Medición
7. Fase de Análisis
8. Fase de Mejora
9. Fase de Control
10. Empresa Lean
2

3. 7. Metodología Seis Sigma
Fase de análisis
Primitivo Reyes A. / Noviembre 2004
3

4. 7. Fase de Análisis
 Propósitos y salidas
 Estudios de R&R por atributos
 Análisis del Modo y Efecto de Falla (AMEF)
 Herramientas para la fase de análisis
 Verificación de causas raíz
4

5. Fase de Análisis
 Propósitos:
 Establecer hipótesis sobre las posibles Causas Raíz
 Refinar, rechazar, o confirmar la Causa Raíz
 Seleccionar las Causas Raíz más importantes:
 Las pocas Xs vitales
 Salidas:
 Causas raíz validadas
 Factores de variabilidad identificados
5

6. Estudios de R&R por atributos
6

7. Aplicación Transaccional de
Repetibilidad y Reproducibilidad
Ejemplo de Administración de Programa:
 A lo largo de la duración de un Programa…
 Se proyecta el tiempo necesario para alcanzar una
meta en particular.
 Se registra el tiempo que tomó en realidad alcanzar la
meta.
 Se calcula la diferencia entre el tiempo proyectado y el
real. Los datos a usar son “número de semanas de
atraso”.
7

8. Datos de GR&R
(Número de Semanas de Atraso)
Programas Gerente de Comprador
Los datos son “número
Programa de semanas de atraso”
1 0 -37 para la selección de
2 1 91 proveedores.
3 6 124
4 0 68 Observe cuan diferente
5 0 -24 miden el mismo evento
6 23 45 el Comprador y el
7 23 19 Gerente de Programa.
8 0 66
9 69 86
10 14 86
8

9. Resultado de Minitab®
GR&R (ANOVA) para las Semanas de Atraso
Componenentes de Variación
100 %Contribución
Porcentaje
%Var. Estudio
50
Interacción de Programas de Operadores
Operadores
0 1
100
GR&R Repetib Reprod Parte a Parte 2
Promedio
50
Gráfica de barras X por Operadores
150 0
1 2
Sample Mean
100
Programas 1 2 3 4 5 6 7 8 9 10
50
0
-50
0
9

10. Resultados de GR&R
Gage R&R
Source Variance %Contribution
Total Gage R&R 1948.0 88.52
Repeatability 0.0 0.00
Reproducibility 1947.9 88.52
Part-To-Part 252.7 11.48
Total Variation 2200.6 100.00
 El 88.52% de la variación observada se debe a la diferencia de
la medición del mismo evento entre el Comprador y el Gerente
de Programa.
 El 11.48% de la variación observada se debe a la diferencia
entre los programas.
¿Es adecuado el sistema actual de medición?
10

11. ¿Por Qué la Inconsistencia en la Medición?
Para poder mejorar el sistema de medición, primero
debemos comprender las causas de la inconsistencia, en
este caso.
• Cuando se les preguntó, “¿En que fecha se seleccionaron los
proveedores finales?”, el Gerente del Programa y el Comprador
percibieron la pregunta de manera distinta.
• El Gerente del Programa pensó que la pregunta se refería a,
¿Cuándo empezamos a trabajar con el proveedor?
• El Comprador creyó que quería decir, ¿Cuándo se emitió la Orden
de Compra?
• Además, hubo confusión en el significado real de “proveedores
finales”. ¿Se refiere a 100% de los proveedores? ¿90%? ¿Sólo son
proveedores de componentes principales?
11

12. Mejora del Sistema de Medición
 Para evitar ambigüedades, el equipo desarrolló la
siguiente definición operacional para la “ Fecha
cuando se seleccionaron los proveedores finales”:
La fecha en que se envió la notificacion escrita de la
selección de proveedores por parte del Departamento de
Compras al último proveedor seleccionado para
suministrar los siguientes componentes:
Estructuras, Mecanismos, Partes, Plásticas
Uretano, Telas
12

13. Estudio de Repetibilidad y
Reproducibilidad de Atributos
 También es muy importante tener adecuada repetibilidad
y reproducibilidad al obtener datos de atributos.
 Si un ejecutivo, decide que una unidad tiene un defecto o
error y otro concluye que la misma unidad no tiene
defectos, entonces hay problema con el sistema de
medición.
 Igualmente, el sistema de medición es inadecuado
cuando la misma persona llega a diferentes conclusiones
al repetir las evaluaciones en la misma unidad o
producto.
13

14. Sistema de Medición de Atributos
 Un sistema de medición de atributos compara
cada parte con un estándar y acepta la parte si
el estándar se cumple.
 La efectividad de la discriminación es la habilidad
del sistema de medición de atributos para
discriminar a los buenos de los malos.
14

15. Estudio de Repetibilidad y
Reproducibilidad de Atributos
1. Selecciona un mínimo de 30 unidades del proceso. Estas
unidades deben representar el espectro completo de la
variación del proceso (buenas, erroneas y en límites).
2. Un inspector “experto” realiza una evaluación de cada
parte, clasificándola como “Buena” o “No Buena”.
3. Cada persona evaluará las unidades, independientemente
y en orden aleatorio, y las definirá como “Buenas” o “No
Buenas”.
4. Ingresa los datos en el archivo Attribute Gage R&R.xls
para cuantificar la efectividad del sistema de medición.
15

16. GR&R de Atributos - Ejemplo
Legenda de Atributos REPORTE
G = Bueno FECHA:
1 NOMBRE:
2
NG = No Bueno PRODUCTO:
SBU:
Esta es la
COND. DE PRUEBA: medida
Población Conocida Persona #1 Persona #2 Acuerdo Acuerdo
Muestra # Atributo #1 #2
general de
#1 #2 Y=Sí N=No Y=Sí N=No
1 G G G G G Y Y consistencia
2 G G G G G Y Y
3 G G G G G Y Y entre los
4
5
G
G
G
G
G
G
G
G
G
G
Y
Y
Y
Y
operadores
6 G NG G G G N N y el “experto”.
7 G G G G G Y Y
8 G G G G G Y Y ¡90% es lo
9 NG G G NG NG N N
10 NG NG NG G G N N mínimo!
11 G G G G G Y Y
12 G G G G G Y Y
13 NG NG NG NG NG Y Y
14 G G G G G Y Y
15 G G G G G Y Y
16 G G G G G Y Y
17 NG NG NG NG NG Y Y
18 G G G G G Y Y
19 G G G G G Y Y
20 G G G G G Y Y
(1)
% DEL EVALUADOR -> 95.00% 100.00%
(2)
% VS. EL ATRIBUTO -> 90.00% 95.00%
(3)
% DE EFECTIVIDAD DE DISCRIMINACION -> 85.00%
(4)
% DE EFECTIVIDAD DE DISCRIMINACION VS. EL ATRIBUTO -> 85.00%
16

17. Interpretación de Resultados
1. % del Evaluador es la consistencia de una persona.
2. % Evaluador vs Atributo es la medida de el acuerdo
que hay entre la evaluación del operador y la del
“experto”.
3. % de Efectividad de Selección es la medida de el
acuerdo que existe entre los operadores.
4. % de Efectividad de Selección vs. el Atributo es una
medida general de la consistencia entre los
operadores y el acuerdo con el “experto”.
17

18. Estudio de Repetibilidad y
Reproducibilidad de Atributos -
Guías de Aceptabilidad
Aunque el 100% es el resultado que deseamos
obtener, en un estudio de repetibilidad y
reproducibilidad de atributos, la siguiente guía se usa
frecuentemente:
Porcentaje Guía
De 90% a 100% Aceptable
De 80% a 90% Marginal
Menos de 80% Inaceptable
18

19. QFD
FASE DE ANÁLISIS
Diagrama de
relaciones
Diagrama
Causa Efecto Diagrama de
Ishikawa
Diagrama
de Árbol
Definición
Y=X1 + X2+. .Xn
CTQs = Ys Medición Y,
Operatividad X1, X2, Xn
X's
Causas
Análisis del Modo y Efecto de potenciales
Falla (AMEF)
Pruebas
de
hipótesis
Diagrama
de Flujo
del X's vitales
proceso No ¿Causa Si Causas raíz
Raíz? validadas
19

20. Pruebas de Hipótesis
Variables Atributos
No Normal Tablas de
Contingencia Chi Cuad.
Varianza Medianas
Correlación
Correlación
Homogeneidad Prueba de signos
de Varianzas
Wilcoxon
Normal Proporciones - Z
de Levene
Mann-
Whitney Variancia Medias
Kurskal-
Wallis 1- Población - Chi Pruebas Z, t
2- Pob. F 1- Población
Residuos
Prueba de Mood 2- Poblaciones
Homogeneidad distribuidos
Friedman de Varianzas ANOVA
de Bartlett Una vía normalmente
Dos vías
Correlación
Regresión 20

21. Análisis del Modo y
Efecto de Falla (AMEF)
21

22. ¿ Qué es el AMEF?
 El Análisis de del Modo y Efectos de Falla es un grupo sistematizado
de actividades para:
 Reconocer y evaluar fallas potenciales y sus efectos.
 Identificar acciones que reduzcan o eliminen las
probabilidades de falla.
 Documentar los hallazgos del análisis.
 Existe el estándar MIL-STD-1629, Procedure for Performing a Failure
Mode, Effects and Criticality Analysis
22

23. Tipos de AMEFs
 FMEA de Diseño (AMEFD), su propósito es analizar
como afectan al sistema los modos de falla y
minimizar los efectos de falla en el sistema. Se usan
antes de la liberación de productos o servicios, para
corregir las deficiencias de diseño.
 FMEA de Proceso (AMEFP), su propósito es analizar
como afectan al proceso los modos de falla y
minimizar los efectos de falla en el proceso. Se usan
durante la planeación de calidad y como apoyo
durante la producción o prestación del servicio.
23

24. AMEFP o AMEF de Proceso
Fecha límite:
Concepto Prototipo Pre-producción /Producción
FMEAD
FMEAP
FMEAD FMEAP
Característica de Diseño Paso de Proceso
Falla Forma en que el Forma en que el proceso falla
producto o servicio falla al producir el requerimiento
que se pretende
Controles Técnicas de Diseño de Controles de Proceso
Verificación/Validación
24

25. Modos de fallas vs
Mecanismos de falla
 El modo de falla es el síntoma real de la falla (altos
costos del servicio; tiempo de entrega excedido).
 Mecanismos de falla son las razones simples o
diversas que causas el modo de falla (métodos no
claros; cansancio; formatos ilegibles) o cualquier otra
razón que cause el modo de falla
25

26. Definiciones
Modo de Falla
- La forma en que un producto o proceso puede fallar para cumplir
con las especificaciones o requerimientos.
- Normalmente se asocia con un Defecto, falla o error.
Diseño Proceso
Alcance insuficiente Omisiones
Recursos inadecuados Monto equivocado
Servicio no adecuado Tiempo de respuesta excesivo
26

27. Definiciones
Efecto
- El impacto en el Cliente cuando el Modo de Falla no se previene
ni corrige.
- El cliente o el siguiente proceso puede ser afectado.
Ejemplos: Diseño Proceso
Serv. incompleto Servicio deficiente
Operación errática Claridad insuficiente
Causa
- Una deficiencia que genera el Modo de Falla.
- Las causas son fuentes de Variabilidad asociada con variables de
Entrada Claves
Ejemplos: Diseño Proceso
Material incorrecto Error en servicio
Demasiado esfuerzo No cumple requerimientos
27

28. Preparación del AMEF
 Se recomienda que sea un equipo
multidisciplinario
 El responsable del sistema, producto o proceso
dirige el equipo, así como representantes de las
áreas involucradas y otros expertos en la materia
que sea conveniente.
28

29. ¿Cuando iniciar un FMEA?
 Al diseñar los sistemas, productos y procesos nuevos.
 Al cambiar los diseños o procesos existentes o que serán
usados en aplicaciones o ambientes nuevos.
 Después de completar la Solución de Problemas (con el fin de
evitar la incidencia del problema).
 El AMEF de diseño, después de definir las funciones del
producto, antes de que el diseño sea aprobado y entregado
para su manufactura o servicio.
 El AMEF de proceso, cuando los documentos preliminares del
producto y sus especificaciones están disponibles.
29

30. ANALISIS DEL MODO Y EFECTO DE FALLA
AMEF de Diseño / Proceso
Componente ______________________ Responsable del Diseño ____________AMEF Número _________________
Ensamble ________________ Preparó _______________ Pagina _______de _______
Equipo de Trabajo ___________ FECHA (orig.) de FMEA ______(rev.) ______
Resultados de Acción
O Controles de D
Función S Causa(s)
Efecto (s) c Diseño o e R Responsable S O D R
del Producto/ Modos de Falla e Potencial(es) Acción Acción
Potencial (es) c Proceso t P y fecha límite e c e P
Paso del Potenciales v o Mecanismos Sugerida Adoptada
de falla u Actuales e N de Terminación v c t N
proceso . de falla
r c
30

31. ANALISIS DEL MODO Y EFECTO DE FALLA
AMEF de Diseño / Proceso
Componente ______________________ Responsable del Diseño ____________AMEF Número _________________
Ensamble ________________ Preparó _______________ Pagina _______de _______
Equipo de Trabajo ___________ FECHA (orig.) de AMEF ______(rev.) ______
Resultados de Acción
O D
Función S Causa(s) Controles del
Efecto (s) c e R Responsable S O D R
de Modos de Falla e Potencial(es) Diseño / Acción Acción
Potencial (es) c t P y fecha límite e c e P
Componente/Paso Potenciales v de los Mecanismos Proceso Sugerida Adoptada
de falla u e N de Terminación v c t N
de proceso . de falla Actual
r c
Factura correcta
Relacione las
funciones del
diseño del
componente
Pasos del proceso
Del diagrama de flujo
31

32. ANALISIS DEL MODO Y EFECTO DE FALLA
AMEF de Diseño / Proceso
Componente ______________________ Responsable del Diseño ____________AMEF Número _________________
Ensamble ________________ Preparó _______________ Pagina _______de _______
Equipo de Trabajo ___________ FECHA (orig.) de AMEF ______(rev.) ______
Resultados de Acción
Función O D
Causa(s) Controles de
del Efecto (s) D c e R Responsable S O D R
Modos de Falla Potencial(es) Diseño / Acción Acción
componente/ Potencial (es) i c t P y fecha límite e c e P
Potenciales de los Mecanismos Proceso Sugerida Adoptada
Paso del de falla v u e N de Terminación v c t N
de falla Actuales
proceso r c
Factura
correcta
Datos incorrectos Identificar modos
de falla Tipo 1
inherentes al
diseño
32

33. Efecto(s) Potencial(es) de falla
Evaluar 3 (tres) niveles de Efectos del Modo de Falla
• Efectos Locales
– Efectos en el Área Local
– Impactos Inmediatos
• Efectos Mayores Subsecuentes
– Entre Efectos Locales y Usuario Final
• Efectos Finales
– Efecto en el Usuario Final del producto o Servicio
33

34. ANALISIS DEL MODO Y EFECTO DE FALLA
AMEF de Diseño
Componente ______________________ Responsable del Diseño ____________AMEF Número _________________
Ensamble ________________ Preparó _______________ Pagina _______de _______
Equipo de Trabajo ___________ FECHA (orig.) de AMEF ______(rev.) ______
Resultados de Acción
O Controles de D
Función Causa(s)
Efecto (s) D c Diseño / e R Responsable S O D R
del componente Modos de Falla Potencial(es) Acción Acción
Potencial (es) i c Proceso t P y fecha límite e c e P
/ Paso del Potenciales oMecanismos Sugerida Adoptada
de falla v u Actuales e N de Terminación v c t N
proceso de falla
r c
Factura correcta Datos incorrectosLOCAL:
Rehacer
la factura
Describir los efectos de
MAXIMO PROXIMO modo de falla en:
Contabilidad LOCAL
equivocada El mayor subsecuente
Y Usuario final
CON CLIENTE
Molestia
Insatisfacción
CTQs del QFD o
Matriz de Causa Efecto
34

35. Rangos de Severidad (AMEFD)
Efecto Rango Criterio .
No 1 Sin efecto
Muy poco 2 Cliente no molesto. Poco efecto en el desempeño del componente o
servicio.
Poco 3 Cliente algo molesto. Poco efecto en el desempeño del comp. o
servicio.
Menor 4 El cliente se siente un poco fastidiado. Efecto menor en el desempeño
del componente o servicio.
Moderado 5 El cliente se siente algo insatisfecho. Efecto moderado en el
desempeño del componente o servicio.
Significativo 6 El cliente se siente algo inconforme. El desempeño del comp. o
servicio se ve afectado, pero es operable y está a salvo. Falla parcial,
pero operable.
Mayor 7 El cliente está insatisfecho. El desempeño del servicio se ve
seriamente afectado, pero es funcional y está a salvo. Sistema afectado.
Extremo 8 Cliente muy insatisfecho. Servicio inadecuado, pero a salvo. Sistema
inoperable.
Serio 9 Efecto de peligro potencial. Capaz de descontinuar el uso sin perder
tiempo, dependiendo de la falla. Se cumple con el reglamento del
gobierno en materia de riesgo.
Peligro 10 Efecto peligroso. Seguridad relacionada - falla repentina.
Incumplimiento con reglamento del gobierno. 35

36. CRITERIO DE EVALUACIÓN DE SEVERIDAD SUGERIDO PARA AMEFP
Esta calificación resulta cuando un modo de falla potencial resulta en un defecto con un cliente final y/o una planta de manufactura
/ ensamble. El cliente final debe ser siempre considerado primero. Si ocurren ambos, use la mayor de las dos severidades
Efecto en el cliente Efecto en Manufactura /Ensamble
Efecto
Calif.
Peligroso
sin aviso
Calificación de severidad muy alta cuando un modo potencial de
falla afecta la operación segura del producto y/o involucra un no
Puede exponer al peligro al operador (máquina o ensamble)
sin aviso 10
cumplimiento con alguna regulación gubernamental, sin aviso
Peligroso
con aviso
Calificación de severidad muy alta cuando un modo potencial de
falla afecta la operación segura del producto y/o involucra un no
Puede exponer al peligro al operador (máquina o ensamble)
sin aviso 9
cumplimiento con alguna regulación gubernamental, con aviso
Muy alto El producto / item es inoperable ( pérdida de la función
primaria)
El 100% del producto puede tener que ser desechado op
reparado con un tiempo o costo infinitamente mayor 8
Alto El producto / item es operable pero con un reducido nivel de
desempeño. Cliente muy insatisfecho
El producto tiene que ser seleccionado y un parte
desechada o reparada en un tiempo y costo muy alto 7
Modera
do
Producto / item operable, pero un item de confort/conveniencia
es inoperable. Cliente insatisfecho
Una parte del producto puede tener que ser desechado sin
selección o reparado con un tiempo y costo alto 6
Bajo Producto / item operable, pero un item de confort/conveniencia
son operables a niveles de desempeño bajos
El 100% del producto puede tener que ser retrabajado o
reparado fuera de línea pero no necesariamente va al àrea 5
de retrabajo .
Muy bajo No se cumple con el ajuste, acabado o presenta ruidos y
rechinidos. Defecto notado por el 75% de los clientes
El producto puede tener que ser seleccionado, sin
desecho, y una parte retrabajada 4
Menor No se cumple con el ajuste, acabado o presenta ruidos y
rechinidos. Defecto notado por el 50% de los clientes
El producto puede tener que ser retrabajada, sin
desecho, en línea, pero fuera de la estación 3
Muy
menor
No se cumple con el ajuste, acabado o presenta ruidos, y
rechinidos. Defecto notado por clientes muy críticos (menos del
El producto puede tener que ser retrabajado, sin desecho
en la línea, en la estación 2
25%)
Ninguno Sin efecto perceptible Ligero inconveniente para la operación u operador, o sin
efecto 1
36

37. ANALISIS DEL MODO Y EFECTO DE FALLA
AMEF de Diseño / Proceso
Componente ______________________ Responsable del Diseño ____________AMEF Número _________________
Ensamble ________________ Preparó _______________ Pagina _______de _______
Equipo de Trabajo ___________ FECHA (orig.) de AMEF ______(rev.) ______
Resultados de Acción
O D
Función S Causa(s) Controles de
Efecto (s) c e R Responsable S O D R
del componente Modos de Falla e Potencial(es) Diseño / Acción Acción
Potencial (es) c t P y fecha límite e c e P
/ Paso del Potenciales v o Mecanismos Proceso Sugerida Adoptada
de falla u e N de Terminación v c t N
proceso . de falla Actuales
r c
La abertura del
engrane propor La abertura no LOCAL:
ciona una aber- es suficiente Daño a sensor
tura de aire entre de velocidad y
diente y diente engrane
Usar tabla para
MAXIMO PROXIMO
Falla en eje 7 determinar severidad o
gravedad
CON CLIENTE
Equipo
parado
37

38. Identificar Causa(s) Potencial(es) de la Falla
• Causas relacionadas con el diseño - Características del
servicio o Pasos del proceso
– Diseño de formatos
– Asignación de recursos
– Equipos planeados
• Causas que no pueden ser Entradas de Diseño,
tales como:
– Ambiente, Clima, Fenómenos naturales
• Mecanismos de Falla
– Rendimiento, tiempo de entrega, información completa
38

39. ANALISIS DEL MODO Y EFECTO DE FALLA
AMEF de Diseño
Componente ______________________ Responsable del Diseño ____________AMEF Número _________________
Ensamble ________________ Preparó _______________ Pagina _______de _______
Equipo de Trabajo ___________ FECHA (orig.) de AMEF ______(rev.) ______
Resultados de Acción
O D
S Causa(s) Controles de
Función Efecto (s) c e R Responsable S O D R
Modos de Falla e Potencial(es) Diseño/Proces Acción Acción
de Potencial (es) c t P y fecha límite e c e P
Potenciales v de los Mecanismos o Actuales Sugerida Adoptada
Artículo de falla u e N de Terminación v c t N
. de falla
r c
Factura correcta Datos incorrectosLOCAL:
Rehacer la Identificar causas
factura
de diseño, y
mecanismos de
MAXIMO PROXIMO falla que pueden
Contabilidad 7
erronea ser señalados para
los modos de falla
CON CLIENTE
Molestia
identificada.
Causas potenciales
Insatisfacción
De Diagrama de Ishikawa
Diagrama de árbol o
Diagrama de relaciones
39

40. Rangos de Ocurrencia (AMEFD)
Ocurrencia Criterios Rango Probabilidad de Falla
Remota Falla improbable. No existen fallas 1 <1 en 1,500,000 Zlt > 5
asociadas con este producto o con
un producto / Servicio casi idéntico
Muy Poca Sólo fallas aisladas asociadas con 2 1 en 150,000 Zlt > 4.5
este producto / Servicio
casi idéntico
3 1 en 30,000
Poca Fallas aisladas asociadas con Zlt > 4
productos / Servicios similares
Moderada Este producto / Servicio ha
tenido fallas ocasionales 4 1 en 4,500 Zlt > 3.5
5 1 en 800 Zlt > 3
Alta Este producto / Servicio ha
6 1 en 150 Zlt > 2.5
fallado a menudo
7 1 en 50 Zlt > 2
Muy alta La falla es casi inevitable
8 1 en 15 Zlt > 1.5
9 1 en 6 Zlt > 1
10 >1 en 3 Zlt < 1
Nota:
El criterio se basa en la probabilidad de ocurrencia de la causa/mecanismo.
Se puede basar en el desempeño de un diseño similar en una aplicación
similar.

41. CRITERIO DE EVALUACIÓN DE OCURRENCIA SUGERIDO PARA AMEFP
Probabilidad Indices Posibles de ppk Calif.
falla
Muy alta: Fallas 100 por mil piezas < 0.55 10
persistentes
50 por mil piezas > 0.55 9
Alta: Fallas frecuentes 20 por mil piezas > 0.78 8
10 por mil piezas > 0.86 7
Moderada: Fallas 5 por mil piezas > 0.94 6
ocasionales
2 por mil piezas > 1.00 5
1 por mil piezas > 1.10 4
Baja : Relativamente pocas 0.5 por mil piezas > 1.20 3
fallas
0.1 por mil piezas > 1.30 2
Remota: La falla es < 0.01 por mil piezas > 1.67 1
improbable
41

42. ANALISIS DEL MODO Y EFECTO DE FALLA
AMEF de Diseño / Proceso
Componente ______________________ Responsable del Diseño ____________AMEF Número _________________
Ensamble ________________ Preparó _______________ Pagina _______de _______
Equipo de Trabajo ___________ FECHA (orig.) de AMEF ______(rev.) ______
Resultados de Acción
Función O D
S Causa(s) Controles de
del Efecto (s) c e R Responsable S O D R
Modos de Falla e Potencial(es) Diseño/ Acción Acción
Componente / Potencial (es) c t P y fecha límite e c e P
Potenciales v o Mecanismos Proceso Sugerida Adoptada
Paso del de falla u e N de Terminación v c t N
. de falla Actuales
proceso r c
Factura correcta Datos LOCAL:
equivocadso Rehacer la
factura
Rango de
probabilidades en que
MAXIMO PROXIMO la causa identificada
Contabilidad 7 3 ocurra
erronea
CON CLIENTE
Molestia
Insatisfacción
42

43. Identificar Controles de Diseño o de
Proceso Actuales
• Verificación/ Validación de actividades de Diseño o
control de proceso usadas para evitar la causa,
detectar falla anticipadamente, y/o reducir impacto:
Cálculos, Análisis, Prototipo de Prueba, Pruebas piloto
Poka Yokes, planes de control, listas de verificación
• Primera Línea de Defensa - Evitar o eliminar causas de falla o error
• Segunda Línea de Defensa - Identificar o detectar fallas o errores
Anticipadamente
• Tercera Línea de Defensa - Reducir impactos/consecuencias de falla o
errores
43

44. ANALISIS DEL MODO Y EFECTO DE FALLA
AMEF de Diseño
Componente ______________________ Responsable del Diseño ____________AMEF Número _________________
Ensamble ________________ Preparó _______________ Pagina _______de _______
Equipo de Trabajo ___________ FECHA (orig.) de AMEF ______(rev.) ______
Resultados de Acción
Función O D
S Causa(s) Controles de
del Efecto (s) c e R Responsable S O D R
Modos de Falla e Potencial(es) Diseño / Acción Acción
Componente / Potencial (es) c t P y fecha límite e c e P
Potenciales v o Mecanismos Proceso Sugerida Adoptada
Paso del de falla u e N de Terminación v c t N
. de falla Actuales
proceso r c
Factura correcta Datos correctos LOCAL:
Rehacer la
factura
¿Cuál es el método de
control actual que usa
MAXIMO PROXIMO ingeniería para evitar el
Contabilidad 7 3 modo de falla?
erronea
CON CLIENTE
Molestia
Insatisfacción
44

45. Rangos de Detección (AMEFD)
• Rango de Probabilidad de Detección basado en la
efectividad del Sistema de Control Actual; basado en el
cumplimiento oportuno con el Plazo Fijado
1 Detectado antes del prototipo o prueba piloto
2-3 Detectado antes de entregar el diseño
4-5 Detectado antes del lanzamiento del servicio
6-7 Detectado antes de la prestación del servicio
8 Detectado antes de prestar el servicio
9 Detectado en campo, pero antes de que ocurra la falla o error
10 No detectable hasta que ocurra la falla o error en campo

46. CRITERIO DE EVALUACIÓN DE DETECCION SUGERIDO PARA AMEFP
Detecciòn Criterio Tipos de Métodos de seguridad de Rangos de Calif
Inspección Detección
A B C
Casi Certeza absoluta de no detección X No se puede detectar o no es verificada
imposible
10
Muy Los controles probablemente no X El control es logrado solamente con
remota detectarán
9
verificaciones indirectas o al azar
Remota Los controles tienen poca X El control es logrado solamente con
oportunidad de detección
8
inspección visual
Muy baja Los controles tienen poca X El control es logrado solamente con
oportunidad de detección
7
doble inspección visual
Baja Los controles pueden detectar X X El control es logrado con métodos gráficos con 6
el CEP
Moderada Los controles pueden detectar X El control se basa en mediciones por variables después de que las
partes dejan la estación, o en dispositivos Pasa NO pasa realizado en 5
el 100% de las partes después de que las partes han dejado la
estación
Moderada Los controles tienen una buena X X Detección de error en operaciones subsiguientes, o medición
mente oportunidad para detectar
realizada en el ajuste y verificación de primera pieza ( solo para 4
causas de ajuste)
Alta
Alta Los controles tienen una buena X X Detección del error en la estación o detección del error en
oportunidad para detectar
operaciones subsiguientes por filtros multiples de aceptación: 3
suministro, instalación, verificación. No puede aceptar parte
discrepante
Muy Alta Controles casi seguros para X X
detectar
Detección del error en la estación (medición automática
con dispositivo de paro automático). No puede pasar la 2
parte discrepante
Muy Alta Controles seguros para detectar X No se pueden hacer partes discrepantes porque el item ha
pasado a prueba de errores dado el diseño del 1
proceso/producto
Tipos de inspección: A) A prueba de error B) Medición automatizada C) Inspección visual/manual 46

47. ANALISIS DEL MODO Y EFECTO DE FALLA
AMEF de Diseño / Proceso
Componente ______________________ Responsable del Diseño ____________AMEF Número _________________
Ensamble ________________ Preparó _______________ Pagina _______de _______
Equipo de Trabajo ___________ FECHA (orig.) de AMEF ______(rev.) ______
Resultados de Acción
Función O D
S Causa(s) Controles de
del Efecto (s) c e R Responsable S O D R
Modos de Falla e Potencial(es) Diseño / Acción Acción
Componente / Potencial (es) c t P y fecha límite e c e P
Potenciales v o Mecanismos Proceso Sugerida Adoptada
Paso del de falla u e N de Terminación v c t N
. de falla Actuales
proceso r c
Factura correcta Datos incorrectosLOCAL:
Rehacer la
factura
¿Cuál es la probabilidad
MAXIMO PROXIMO
de detectar la causa de
Contabilidad 7 3 5
falla?
erronea
CON CLIENTE
Molestia
Insatisfacción
47

48. Calcular RPN (Número de Prioridad de
Riesgo)
Producto de Severidad, Ocurrencia, y Detección
RPN / Gravedad usada para identificar principales CTQs
Severidad mayor o igual a 8
RPN mayor a 150
48

49. ANALISIS DEL MODO Y EFECTO DE FALLA
AMEF de Diseño / Proceso
Componente ______________________ Responsable del Diseño ____________ AMEF Número _________________
Ensamble ________________ Preparó _______________ Pagina _______de _______
Equipo de Trabajo ___________ FECHA (orig.) de AMEF ______(rev.) ______
Resultados de Acción
O D
S Causa(s)
Función Efecto (s) c e R Responsable S O D R
Modos de Falla e Potencial(es) Controles de Acción Acción
de Potencial (es) c t P y fecha límite e c e P
Potenciales v de los Mecanismos Diseño Actual Sugerida Adoptada
Artículo de falla u e N de Terminación v c t N
. de falla
r c
Factura Datos LOCAL:
incorrecta incorrectos Rehacer
la factura
Riesgo = Severidad x
MAXIMO PROXIMO Ocurrencia x Detección
Contabilidad 7 3 5 105
erronea
CON CLIENTE
Molestia
Causas probables a
Insatisfacción
atacar primero
49

50. Planear Acciones
Requeridas para todos los CTQs
 Listar todas las acciones sugeridas, qué persona
es la responsable y fecha de terminación.
 Describir la acción adoptada y sus resultados.
 Recalcular número de prioridad de riesgo .
Reducir el riesgo general del diseño
50

51. ANALISIS DEL MODO Y EFECTO DE FALLA
AMEF de Diseño / Proceso
Componente ______________________ Responsable del Diseño ____________ AMEF Número _________________
Ensamble ________________ Preparó _______________ Pagina _______de _______
Equipo de Trabajo ___________ FECHA (orig.) de AMEF ______(rev.) ______
Resultados de Acción
O D
Función S Causa(s) Controles de
Efecto (s) c e R Responsable S O D R
del componente Modos de Falla e Potencial(es) Diseño / Acción Acción
Potencial (es) c t P y fecha límite e c e P
/ Paso del Potenciales v o Mecanismos Prcoeso Sugerida Adoptada
de falla u e N de Terminación v c t N
proceso . de falla Actuales
r c
Factura correcta Datos LOCAL:
erroneos Rehacer la
factura
MAXIMO PROXIMO
Contabilidad 7 3 5 105
erronea
CON CLIENTE
Molestia
Insatisfacción Usar RPN para identificar
acciones futuras. Una vez que
se lleva a cabo la acción,
recalcular el RPN.
51

52. Ejemplo de AMEFP
52

53. Herramientas de la
Fase de Análisis
Identificación de causas potenciales
Cartas Multivari y Análisis de Regresión
Intervalos de confianza y Pruebas de Hipótesis
53

54. Identificación de causas
potenciales
Tormenta de ideas
Diagrama de Ishikawa
Diagrama de Relaciones
Diagrama de Árbol
Verificación de causas raíz
54

55. Tormenta de ideas
 Técnica para generar ideas creativas cuando la mejor
solución no es obvia.
 Reunir a un equipo de trabajo (4 a 10 miembros) en
un lugar adecuado
 El problema a analizar debe estar siempre visible
 Generar y registrar en el diagrama de Ishikawa un
gran número de ideas, sin juzgarlas, ni criticarlas
 Motivar a que todos participen con la misma
oportunidad 55

56. Tormenta de ideas
 Permite obtener ideas de los participantes
56

57. Diagrama de Ishikawa
 Anotar el problema en el cuadro de la derecha
 Anotar en rotafolio las ideas sobre las posibles causas
asignándolas a las ramas correspondientes a:
 Medio ambiente
 Mediciones
 Materia Prima
 Maquinaria
 Personal y
 Métodos
o
 Las diferentes etapas del proceso de manufactura o
servicio
57

58. Diagrama de Ishikawa
Medio
ambiente Métodos Personal
Frecuencia Falta de
Rotación de
Clima personal
de visitas supervi
húmedo Falta de
ción
motivación
Posición de Ausentismo
Distancia de exhibidores
la agencia al
Elaboración ¿Qué
changarro de pedidos produce
bajas ventas
Clientes con Calidad del de
ventas bajas Seguimiento producto Tortillinas
Malos
semanal Tía Rosa?
Conocimiento
itinerarios
de los Tipo de
Descompostura mínimos por exhibidor
del camión ruta
repartidor
Maquinaría Medición Materiales
58

59. Diagrama de relaciones Perdida de mercado
debido a la
competencia
No hay flujo
efectivo de mat. Influencia de la Compra de material
Por falta de situación econ del para el desarrollo de
programación país nuevos productos por
de acuerdo parte inv..... Y desarrollo’’’
No hay coordinación
a pedidos entre marketing
Falta de operaciones
No hay control coordinación al fincar
de inv..... En proc. pedidos entre
Constantes
Falta de prog. De marketing y la op.
cancelaciones
la op. En base a No hay coordinación
de pedidos
los pedidos entre la operación y las unidades
de marketing
Programación del negocio
Las un. Reciben
deficiente
ordenes de dos
deptos diferentes
Capacidad
instalada Falta de coordinación
desconocida entre el enlace de compras
Altos Duplicidad Demasiados deptos
de cada unidad con compras
Falta de control de inventarios de funciones de inv..... Y desarrollo
corporativo
inventarios en
Compras
compras
aprovecha
Falta de com..... Entre
ofertas No hay com..... Entre
las dif. áreas de
las UN y la oper.
la empresa
Marketing no
Mala prog. De tiene en cuenta
ordenes de compra cap de p.
No hay com..... Entre compras
con la op. general
Influencia directa de
marketing sobre
compras
Falta de comunicación
entre las unidades
del negocio
59

60. ¿Que nos puede provocar Variación de Velocidad
Durante el ciclo de cambio en la sección del Embobinadores?
13/0 2/1
Bandas de
Dancer transmisión
2/4 Taco generador 1/1 Causas a validar
del motor Empaques de arrastre
0/4 Poleas guías 0/3
Presión de aire de trabajo
1/2 Presión del 5/2
Drive principal
dancer
5/1 Mal guiado 4/1
Voltaje del motor
1/4 Sensor de velocidad
de línea 1/5 principales
Ejes
Entradas Causa
Salidas Efecto
1/4 Sensor
1/5
Poleas de transmisión
circunferencial
60

61. Diagrama de árbol o sistemático
Meta Medio
Meta Medio
Meta Medio
Segundo Tercer Cuarto
Primer nivel nivel nivel
nivel
Medios
Medios
Medios
Medios
o planes
Meta u
objetivo
Medios
o planes
61

62. Diagrama de Arbol- Aplicación Sistema SMED
¿Cómo? ¿Cuándo?
Filmar la preparación 5- 12 - Mar-04
Preparación
para el SMED
Analizar el video 10 y 17 –Mar-04
Describir las tareas 17- Mar-04
¿Objetivo? Separar las tareas 17- Mar-04
Fase 1: Separación
de la preparación Elaborar lista de chequeo 2- Mar-04
Implantar el interna de la externa
Sistema Realizar chequeo de
24- Mar-04
funciones
SMED
Producto DJ Analizar el transporte de
24- Mar-04
2702 herramientas y materiales
Analizar las funciones y
¿Qué? Fase 2: Conversión propósito de c/operación
12 - Abr- 04
de preparación
Convertir tareas de prepa-
interna en externa ración interna a externas
15 –Abr - 04
Elaboramos un
Diagrama de Arbol Realización de operaciones
5 –May -04
en paralelo.
para poder
analizar nuestro Fase 3: Refinamiento
Uso de sujeciones
problema siguiendo de todos los aspectos funcionales.
19– May -04
el sistema SMED. de la preparación.
Eliminación de ajustes 12- May -04
62 19

63. Verificación de posibles causas
 Para cada causa probable , el equipo deberá
por medio del diagrama 5Ws – 1H:
 Llevar a cabo una tormenta de ideas para
verificar la causa.
 Seleccionar la manera que:
 represente la causa de forma efectiva, y
 sea fácil y rápida de aplicar.
63

64. Calendario de las actividades
¿qué? ¿por qué? ¿cómo? ¿cuándo ¿dónde ¿quién?
? ?
1 1.1 Por variación de 1.1.1 Tomar dimensiones de ensamble entre Abril ’04 1804 J. R.
Tacogenerador voltaje durante el coples. Embob.
de motor ciclo de cambio 1.1.2 Verificar estado actual y
embobinador especificaciones de escobillas.
1.1.3 tomar valores de voltaje de salida
durante el ciclo de cambio.
2 Sensor 2.1 Por que nos 2.1.1 Tomar dimensiones de la distancia Abril ’04 1804 U. P.
circular y de genera una varión en entre poleas y sensores. Embob.
velocidad de la señal de referencia 2.1.2 Tomar valores de voltaje de salida de
linea. hacia el control de los sensores.
velocidad del motor 2.1.3 Verificar estado de rodamientos de
embobinador poleas.
3 Ejes 3.1 Por vibración 3.1.1 Tomar lecturas de vibración en Abril’04 1804 F. F.
principales de excesiva durante el alojamientos de rodamientos Embob.
transmisión. ciclo de cambio 3.1.2 Comparar valores de vibraciones con
lecturas anteriores.
3.1.3 Analizar valor lecturas de vibración
tomadas.
4 Poleas de 4.1 Puede generar 4.1.1 Verificar alineación, entre poleas de Abril’04 1804 J. R.
transmisión de vibración excesiva ejes principales y polea de transmisión del Embob. U. P.
ejes durante el ciclo de motor.
embobinadores cambio. 4.1.2 Tomar dimensiones de poleas(dientes
. de transmisión).
4.1.3 Tomar dimensiones de bandas (dientes
de transmisión)
4.1.4 Verificar valor de tensión de bandas. 64

65. Modelando relaciones entre
variables
Cartas Multivari
y
Análisis de regresión
65

66. Cartas Multivari
 Su propósito fundamental es reducir el gran número de
causas posibles de variación, a un conjunto pequeño de
causas que realmente influyen en la variabilidad.
 Sirven para identificar patrones de variación:
 Temporal: Variación de hora a hora; turno a
turno; día a día; semana a semana; etc.
 Cíclico: Variación entre unidades de un mismo
proceso; variación entre grupos de unidades;
variación de lote a lote.
 Posicional: Dentro de la pieza
66

67. Cartas Multivari
8 AM 9 AM 10 AM 11 AM 12 AM
2.0 dias
1.5 días
1.0 días
Zona A
Zona B
Zona D
Zona C
67

68. Zona orden Tipo de orden
Tiempo
respuesta
3 1 23
Corrida en Minitab
3 1 20
3 1 21
3 2 22
3 2 19
3 2 20
 Se introducen los datos en varias 3 3 19
columnas C1 a C3 incluyendo la 3
3
3
3
18
21
respuesta (tiempo) y los factores 1 1 22
1 1 20
(Zona y Tipo de orden) 1 1 19
1 2 24
1 2 25
1 2 22
1 3 20
1 3 19
1 3 22
2 1 18
2 1 18
2 1 16
2 2 21
2 2 23
2 2 20
2 3 20
2 3 22
2 3 68 24

69. Corrida en Minitab
 Utilizar el archivo de ejemplo orden.mtw
 Opción: Stat > Quality Tools > Multivari charts
 Indicar la columna de respuesta y las columnas de
los factores
 En opciones se puede poner un título y conectar las
líneas
69

70. Resultados
Multi-Vari Chart for Tiempo respuesta by Zona orden - Tipo de orden
24 Zona
orden
1
23
2
3
22
Tiempo respuesta
21
20
19
18
17
1 2 3
Tipo de orden
70

71. Análisis de Regresión
El análisis de regresión es un método
estandarizado para localizar la correlación entre dos
grupos de datos, y, quizá más importante, crear un
modelo de predicción.
Puede ser usado para analizar las relaciones entre:
• Una sola “X” predictora y una sola “Y”
• Múltiples predictores “X” y una sola “Y”
• Varios predictores “X” entre sí
71

72. Definiciones
Correlación
Establece si existe una relación entre las variables y
responde a la pregunta, ”¿Qué tan evidente es esta
relación?"
Regresión
Describe con más detalle la relación entre las variables.
Construye modelos de predicción a partir de información
experimental u otra fuente disponible.
Regresión lineal simple
Regresión lineal múltiple
Regresión no lineal cuadrática o cúbica
72

73. Correlación de la información de las X y las Y
Correlación Positiva Correlación Negativa
25
Evidente 25
Evidente
20 20
15 15
10
Y
Y
10
5
5
0
0 5 10 15 20 25
Sin Correlación 0
0 5 10 15 20 25
X 25 X
20
15
Correlación Y 10
Correlación
5
25
Positiva 0 Negativa
0 5 10 15 20 25 25
20
X 20
15
15
Y
10
Y
10
5
5
0
0 5 10 15 20 25 0
0 5 10 15 20 25
X
X
73

74. Ejemplo
Considere el problema de predecir las ventas mensuales
(score2) en función del costo de publicidad (Score 1). Calcular
el coeficiente de correlación, el de determinación y la recta.
Score1 Score2
4.1 2.1
2.2 1.5
2.7 1.7
6 2.5
8.5 3
4.1 2.1
9 3.2
8 2.8
7.5 2.5
74

75. Corrida en Minitab
 Utilizar el archivo de ejemplo Exh_regr.mtw
 Opción: Stat > Regression > Regression
 Para regresión lineal indicar la columna de respuesta
Y (Score2) y X (Score1)
 En Regresión lineal en opciones se puede poner un
valor Xo para predecir la respuesta e intervalos. Las
gráficas se obtienen Stat > Regression > Regression
> Fitted line Plots
 Para regresión múltiple Y (heatflux) y las columnas
de los predictores X´s (north, south, east)
75

76. Resultados de la regresión lineal
Regression Analysis: Score2 versus Score1
The regression equation is
Score2 = 1.12 + 0.218 Score1
Predictor Coef SE Coef T P
Constant 1.1177 0.1093 10.23 0.000
Score1 0.21767 0.01740 12.51 0.000
S = 0.127419 R-Sq = 95.7% R-Sq(adj) =
95.1%
Analysis of Variance
Source DF SS MS F P
Regression 1 2.5419 2.5419 156.56 0.000
Residual Error 7 0.1136 0.0162
Total 8 2.6556 76

77. Resultados de la regresión lineal
Fitted Line Plot
Score2 = 1.118 + 0.2177 Score1
3.5 Regression
95% CI
95% PI
3.0 S 0.127419
R-Sq 95.7%
R-Sq(adj) 95.1%
2.5
Score2
2.0
1.5
1.0
2 3 4 5 6 7 8 9
Score1
77

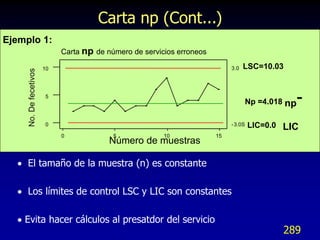
78. Interpretación de los Resultados
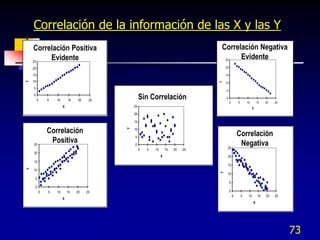
La ecuación de regresión (Score2 = 1.12 + 0.218 Score1)
describe la relación entre la variable predictora X y la respuesta de
predicción Y.
R2 (coef. de determinación) es el porcentaje de variación
explicado por la ecuación de regresión respecto a la variación total
en el modelo
El intervalo de confianza es una banda con un 95% de
confianza de encontrar la Y media estimada para cada valor de
X [Líneas rojas]
El intervalo de predicción es el grado de certidumbre de la
difusión de la Y estimada para puntos individuales X. En general,
95% de los puntos individuales (provenientes de la población sobre
la que se basa la línea de regresión), se encontrarán dentro de la
banda [Líneas azules]
78

79. Corrida en Minitab
 Se introducen los datos HeatFlux East South North
en varias columnas C1 a
C5 incluyendo la 271.8 33.53 40.55 16.66
respuesta Y (heatflux) y
264 36.5 36.19 16.46
las variables predictoras
X’s (North, South, East) 238.8 34.66 37.31 17.66
230.7 33.13 32.52 17.5
251.6 35.75 33.71 16.4
257.9 34.46 34.14 16.28
79

80. Resultados de la regresión Múltiple
Regression Analysis: HeatFlux versus East, South, North
The regression equation is
HeatFlux = 489 - 0.28 East + 3.21 South - 20.3 North
Predictor Coef SE Coef T P
Constant 488.74 88.87 5.50 0.032
East -0.278 1.395 -0.20 0.860
South 3.2134 0.5338 6.02 0.027
North -20.293 2.981 -6.81 0.021
S = 3.47637 R-Sq = 98.0% R-Sq(adj) = 95.0%
Analysis of Variance
Source DF SS MS F P
Regression 3 1173.46 391.15 32.37 0.030
Residual Error 2 24.17 12.09
Total 5 1197.63
80

81. Relaciones no Lineales
¿Qué pasa si existe una relación causal, no lineal?
El siguiente es un conjunto de datos Fitted Line Plot
experimentales codificados, sobre Y = 18.13 + 1.089 X
- 0.02210 X**2
resistencia a la compresión de una
35.0 Regression
aleación especial: 95% CI
95% PI
32.5 S 1.35809
Resistencia a R-Sq 66.8%
Concentración la Compresión R-Sq(adj) 61.2%
30.0
x y Y
10.0 25.2 27.3 28.7
27.5
15.0 29.8 31.1 27.8
20.0 31.2 32.6 29.7
25.0 31.7 30.1 32.3 25.0
30.0 29.4 30.8 32.8
10 15 20 25 30
X
81

82. Otros Patrones No Lineales
A veces es posible transformar una o ambas variables, para mostrar
mejor la relación entre ambas. La meta es identificar la relación
matemática entre las variables, para que con la variable transformada
se obtenga una línea más recta. Algunas transformaciones comunes
incluyen:
x’ = 1/x
x’ = Raíz cuadrada de (x)
Funciones trigonométricas: x’ = Seno
de x x’ = log x
82

83. Resumen de la Regresión
• La regresión sólo puede utilizarse con información de
variables continuas.
• Los residuos deben distribuirse normalmente con media
cero.
• Importancia práctica: (R2). Importancia estadística:
(valores p)
• La regresión puede usarse con un “predictor” X o más,
para una respuesta dada
• Reduzca el modelo de regresión cuando sea posible,
sin perder mucha importancia práctica
83

84. Pruebas de hipótesis
para datos normales
Intervalos de confianza
Pruebas de hipótesis
84

85. Estimación puntual
y por intervalo
 Las medias o desviaciones estándar calculadas de
una muestra se denominan ESTADÍSTICOS, son
puntos estimados de la media y desviación estándar
real de población o de los PARAMETROS.
 Si no se desean números sencillos como estimadores
de la media basada en una muestra, entonces se
determina un
“Un Intervalo de Confianza”
85

86. Estimación puntual
y por intervalo
 ¿Cómo obtenemos un intervalo de confianza?
Punto estimado + error estimado del parámetro
 ¿De dónde viene el error estimado?
Desv. estándar X multiplicador de NC (nivel de
confianza) deseado
86

87. Estimación puntual
y por intervalo
 Nivel de significancia Alfa = 1 – NC, para el caso de
NC = 95%, se tiene un alfa de 0.05 o 0.025 de
cada lado.
 Alfa es la probabilidad de que el parámetro esté
fuera del intervalo de confianza.
 Un área de 0.025 en la tabla Z, corresponde a una
Z de 1.960.
87

88. Representación gráfica
Rango en el que se
Encuentra el parámetro
IC = 90, 95 o 99% Con un nivel de confianza NC
n=30
Alfa/2
n=15
n=10
Distribución normal Z Distribución t (gl. = n-1)
88

89. Estimación puntual
y por intervalo
Por Ejemplo:
 Si la media de la muestra es 100 y la desviación
estándar es 10, el intervalo de confianza al 95%
donde se encuentra la media para una distribución
normal es:
100 + (10) X 1.96 => (80.4, 119.6)
Multiplicador de nivel de confianza = Z0.025 = 1.96
89

90. Estimación puntual
y por intervalo
C. I. Multiplicador Zalfa/2 Alfa/2
99 2.576 0.005
95 1.960 0.025
90 1.645 0.05
85 1.439 0.075
80 1.282 0.10
Para tamaños de muestra n>30, la distribución de referencia
es la Normal
Para muestras de menor tamaño n<=30, debe usarse la
distribución t
90

91. Fórmulas de estimación por intervalo

 para.n 30  X  Z 
2 n

 para.n 30  X  t
2 n
( n  1) s 2 ( n  1) s 2
2 

2
2 
, n 1 1 , n 1
2 2
p (1  p )
  p  Z
2
n
91

92. Pruebas de hipótesis para
medias, varianzas y proporciones
92

93. Pruebas de Hipótesis
Variables Atributos
No Normal Tablas de
Contingencia Chi Cuad.
Varianza Medianas
Correlación
Correlación
Homogeneidad Prueba de signos
de Varianzas
Wilcoxon
Normal Proporciones - Z
de Levene
Mann-
Whitney Variancia Medias
Kurskal-
Wallis 1- Población - Chi Pruebas Z, t
2- Pob. F 1- Población
Residuos
Prueba de Mood 2- Poblaciones
Homogeneidad distribuidos
Friedman de Varianzas ANOVA
de Bartlett Una vía normalmente
Dos vías
Correlación
Regresión 93

94. Resumen de pruebas de Hipótesis – Datos normales
Pruebas de Medias
Prueba t de 1 población: Prueba si el promedio de la
muestra es igual a un promedio conocido o meta
conocida.
Prueba t de 2 poblaciones: Prueba si los dos promedios
de las muestras son iguales.
ANOVA de un factor, dirección o vía: Prueba si más de
dos promedios de las muestras son iguales.
ANOVA de dos vías: Prueba si los promedios de las
muestras clasificadas bajo dos categorías, son iguales.
94

95. Resumen de pruebas de Hipótesis – Datos normales
Pruebas de Variancias
Prueba X2: Compara la variancia de una muestra con
una variancia de un universo conocido.
Prueba F: Compara dos varianzas de muestras.
Homogeneidad de la variancia de Bartlett: Compara
dos o más varianzas muestras de la misma población.
Correlación : Prueba la relación lineal entre dos
variables.
Regresión : Define la relación lineal entre una variable
dependiente y una independiente. (Aquí la
"normalidad" se aplica al valor residual de la
regresión) 95

96. Pruebas de Hipótesis
En CADA prueba estadística, se comparan algunos
valores observados a valores esperados de parámetros
(media, desviación estándar, varianza)
Los ESTADÏSTICOS son calculados en base a la
muestra y estiman a los parámetros VERDADEROS
La capacidad para detectar un diferencia entre lo que
es observado y lo que es esperado depende del
tamaño de la muestra, al aumentar mejora la
estimación y la confianza en las conclusiones
estadísticas.
96

97. Pruebas de Hipótesis
Se trata de probar una afirmación sobre parámetros de
la población en base a datos de estadísticos de una
muestra:
Por ejemplo, probar las afirmaciones en los
parámetros:
La media poblacional  = 12;
La proporción poblacional  = 0.3
La Media poblacional 1 = Media poblacional 2
97

98. Conceptos fundamentales
 Hipótesis nula Ho
 Es la hipótesis o afirmación a ser probada
 Puede ser por ejemplo  =, , o  a 5
 Sólo puede ser rechazada o no rechazada
 Hipótesis alterna Ha
 Es la hipótesis que se acepta como verdadera cuando
se rechaza Ho, es su complemento
 Puede ser por ejemplo   5 para prueba de dos
colas
  < 5 para prueba de cola izquierda
  > 5 para prueba de cola derecha
98

99. Conceptos fundamentales
 Estadístico de prueba
 Para probar la hipótesis nula se calcula un estadístico
de prueba con la información de la muestra el cual se
compara a un valor crítico apropiado. De esta forma se
toma una decisión sobre rechazar o no rechazar la Ho
 Error tipo I (alfa = nivel de significancia, normal=.05)
 Se comete al rechazar la Ho cuando en realidad es
verdadera. También se denomina riesgo del productor
 Error tipo II (beta )
 Se comete cuando no se rechaza la hipótesis nula
siendo en realidad falsa. Es el riesgo del consumidor
99

100. Conceptos fundamentales
 Pruebas de una cola
 Si la Ho:  , que un valor poblacional, entonces el
riesgo alfa se coloca en el extremo derecho de la
distribución. Por ejemplo si Ho   10 y Ha:  >10
se tiene una prueba de cola derecha:
Región de
rechazo
P(Z>= + Zexcel ) = alfa
100

101. Conceptos fundamentales
 Pruebas de una cola
 Si la Ho:   que un valor poblacional, entonces el
riesgo alfa se coloca en el extremo izquierdo de la
distribución. Por ejemplo si Ho   10 y Ha:  <
10 se tiene una prueba de cola izquierda:
Región de
rechazo
P(Z<= - Zexcel ) = alfa
Zexcel ( 0.01 )
101

102. Conceptos fundamentales
 Pruebas de dos colas
 Si la Ho:  = que un valor poblacional, entonces el
riesgo alfa se reparte en ambos extremos de la
distribución. Por ejemplo si Ha: ≠ 10 se tiene:
P(Z<= - Zexcel ) = alfa/2 P(Z>= + Zexcel ) = alfa/2
Regiones de rechazo
102

103. Conceptos fundamentales
 El Tamaño de muestra requerido en función del error
máximo E o Delta P intervalo proporcional esperado
se determina como sigue:
Z 2 / 2 2
n
E2
Z 2 / 2 ( p )(1  p )
n
( p ) 2
103

104. Elementos de una Prueba de Hipótesis
Pruebas de Hipótesis de dos colas:
Ho: a = b Región de Región de
Ha: a  b Rechazo Rechazo
-Z 0 Z
Pruebas de Hipótesis de cola derecha:
Ho: a  b
Ha: a > b Región de
Rechazo
0 Z
Pruebas de Hipótesis cola izquierda:
Ho: a  b
Ha: a < b Región de
Rechazo
-Z 0 Z

105. Pasos en la Prueba de Hipótesis
1. Definir el Problema - Problema Práctico
2. Señalar los Objetivos - Problema Estadístico
3. Determinar tipo de datos - Atributo o Variable
4. Si son datos Variables - Prueba de Normalidad
5. Establecer las Hipótesis
- Hipótesis Nula (Ho) - Siempre tiene el signo igual
- Hipótesis Alterna (Ha) – Tiene signos dif., > o <.
6. Seleccionar el nivel de Alfa (normalmente 0.05 o 5%)
105

106. Pasos en la Prueba de Hipótesis
7. Establecer el tamaño de la muestra, >= 10 y colectar
datos.
8. Decidir la prueba estadística apropiada y calcular el
estadístico de prueba (Z, t, X2 or F) a partir de los datos.
9. Obtener el estadístico que define la zona de rechazo ya
sea de tablas o Excel.
10.Comparar el estadístico calculado con el de tablas y ver
si cae en la región de rechazo o ver si la probabilidad es
menor a alfa, rechazar Ho y acepte Ha. En caso contrario no
rechazar Ho.
11.Con los resultados interprete una conclusión estadística
para la solución práctica.
106

107. Estadísticos para
medias, varianzas y proporciones
X 
Z  ;Una.media; n  30;   conocida
/ n
X 
t ;Una.media; n  30;   desconocida
S/ n
S12
F  2 ; DF  n1  1, n2  1; prueba.dos. var ianzas
S2
X1  X 2
t ; dos.medias;  ' s  desconocidas. pero. 
1 1
Sp / 
n1 n2
( n1  1) s1  ( n2  1) s2
2 2
Sp  ; DF  n1  n2  2
n1  n2  2
X1  X 2
t ; dos.medias;  ' s  desconocidas.diferentes
2 2
s s
1
 2
n1 n2
DF  formula.especial 107

108. Estadísticos para medias
pareadas y varianzas
 Para el caso de muestras pareadas se calculan las
diferencias d individuales como sigue:
d
t ; Pares.de.medias; d i . para.cada. par
Sd / n
(n  1) S 2
X2  ; DF  (n  1); prueba.una.v ar ianza
 2
(O  E ) 2
X2  ; DF  (r  1)(c  1); bondad .ajuste
E
108

109. Ejemplo de prueba de hipótesis
Probar la hipótesis de igualdad de una media u para n > 30
1) Ho:  Ha: 
2) Calcular el estadístico de prueba Zc con fórmula
3) Determinar el estadístico de tablas Zt de Excel
4) Establecer la región de rechazo con Zt y ver si cae ahí Zc
Las regiones de rechazo prueba de 2 colas: -Z y Z
5) Determinar el Intervalo de confianza para la media y ver si
incluye a la media de la hipótesis, si no rechazar Ho
6) Determinar el valor P correspondiente a Zc y comparar
contra Alfa/2, si es menor rechazar Ho
109

110. Ejemplo de prueba de hipótesis
 Rechazar Ho si:
 Zc se encuentra en la región de rechazo
 La media de la hipótesis no se encuentra en el
intervalo de confianza
 El valor p de la Zc es menor que alfa/2 o Alfa para una
cola
 Región de
Zcalc= Rechazo Región de
s
Rechazo
n 0
-Z Z
-Zt Zt 110

111. Ejemplo para dos colas
 Supongamos que tenemos muestras de dos reactores que
producen el mismo artículo. Se desea ver si hay diferencia
significativa en el rendimiento de “Reactor a Reactor”.
Reactor A Reactor B
89.7 84.7 Estadísticas Descriptivas
81.4 86.1
84.5 83.2 Variable Reactor N Media Desv.Std
84.8 91.9
87.3 86.3 Rendimiento A 10 84.24 2.90
79.7 79.3 B 10 85.54 3.65
85.1 82.6
81.7 89.1
83.7 83.7
84.5 88.5

112. ¿Qué representa esto?
Reactor A Reactor B
B B B B B BB BB B
A AA AAAA A A
80.0 82.5 85.0 87.5 90.0 92.5
¿Representan los reactores dos procesos diferentes?
¿Representan los reactores el mismo proceso básico?
112

113. Prueba de Hipótesis
Pregunta Práctica: ¿Existe diferencia entre los reactores?
Pregunta estadística:
¿La media del Reactor B (85.54) es significativamente
diferente de la media del Reactor A (84.24)? o su
diferencia se da por casualidad en una variación de día a
día.
113

114. Prueba de Hipótesis
Ho: Hipótesis Nula: Ha: Hipótesis Alterna: Las
No existe diferencia entre medias de los Reactores
los Reactores son diferentes.
Ho:  a   b
Ha:  a   b
Debemos demostrar que los valores que observamos al parecer no
corresponden al mismo proceso, que la Ho debe estar equivocada
114

115. ANOVA de un factor
o dirección
Pruebas de hipótesis de
varias medias a la vez
115

116. ANOVA – Prueba de hipótesis para probar
la igualdad de medias de varias
poblaciones para un factor
Se trata de probar si el efecto de un factor o
Tratamiento en la respuesta de un proceso o sistema es
Significativo, al realizar experimentos variando
Los niveles de ese factor (Temp. 1, Temp. 2, Temp.3, etc.)
Ho : 1   2  3  .........  a
Ha : A lg unas ' s.son.diferentes
.
116

117. ANOVA - Condiciones
 Todas las poblaciones son normales
 Todas las poblaciones tiene la misma varianza
 Los errores son independientes con distribución
normal de media cero
 La varianza se mantiene constante para todos los
niveles del factor
117

118. ANOVA – Ejemplo de datos
Niveles del Factor Peso % de algodón y Resistencia de tela
Cuadrilla Tiempo de respuesta
15 7 7 15 11 9
20 12 17 12 18 18
25 14 18 18 19 19
30 19 25 22 19 23
35 7 10 11 15 11
118

119. ANOVA – Suma de
cuadrados total
Xij
Gran media
Xij
a b 2
SCT    ( Xij  X )
i 1 j 1
119

120. ANOVA – Suma de cuadrados de
renglones (a)-tratamientos
Media Trat. 1 Media Trat. a
a renglones
Gran media
a
Media trat. 2
SCTr   b( X i  X ) 2
i 1
120

121. ANOVA – Suma de cuadrados
del error
X2j X3j
X1j
Media X1.
Media X3.
Media X2.
Muestra 1 Muestra 2 Muestra 3
a b
SCE   (X ij  X i) 2
i 1 j 1 121

122. ANOVA – Suma de cuadrados
del error
X2j X3j
X1j
Media X1.
Media X3.
Media X2.
Muestra 1 Muestra 2 Muestra 3
SCE  SCT  SCTr
122

123. ANOVA – Grados de libertad:
Totales, Tratamientos, Error
gl.SCT  n  1
gl.SCTr  a  1
gl.SCE  (n  1)  (a  1)  n  a
123

124. ANOVA – Cuadrados medios:
Total, Tratamiento y Error
MCT  SCT /(n  1)
MCTr  SCTr /(a  1)
MCE  SCE /(n  a)
124

125. ANOVA – Cálculo del estadístico
Fc y Fexcel
MCTr
Fc 
MCE
Fexcel  FINVALFA, gl .SCTr , gl .SCE
125

126. Tabla final de ANOVA
TABLA DE ANOVA
FUENTE DE VARIACIÓN SUMA DE GRADOS DE CUADRADO VALOR F
CUADRADOS LIBERTAD MEDIO
Entre muestras (tratam.) SCTR a-1 CMTR CMTR/CME
Dentro de muestras (error) SCE n-a CME
Variación total SCT n-1 CMT
Regla: Rechazar Ho si la Fc de la muestra es mayor que la F de Excel para una cierta alfa
o si el valor p correspondiente a la Fc es menor al valor de alfa especificado
126

127. ANOVA – Toma de decisión
Distribución F Fexcel
Alfa
Zona de no rechazo de Ho Zona de rechazo
O de no aceptar Ha De Ho o aceptar Ha
Fc
127

128. ANOVA – Toma de decisión
Si Fc es mayor que Fexcel se rechaza Ho
Aceptando Ha donde las medias son diferentes
O si el valor de p correspondiente a Fc es
menor de Alfa se rechaza Ho
128

129. Corrida en Minitab
 Se introducen las respuestas en una columna C1
 Se introducen los subíndices de los renglones en una
columna C2 Durability Carpet
18.95 1
12.62 1
11.94 1
14.42 1
10.06 2
7.19 2
7.03 2
14.66 2
129

130. Corrida en Minitab
 Opción: stat>ANOVA – One Way (usar archivo
Exh_aov)
 En Response indicar la col. De Respuesta (Durability)
 En factors indicar la columna de subíndices (carpet)
 En comparisons (Tukey)
 Pedir gráfica de Box Plot of data y residuales Normal
Plot y vs fits y orden
 Si los datos están en columnas pedir ANOVA – One
Way (unstacked) 130

131. Resultados
One-way ANOVA: Durability versus Carpet
Source DF SS MS F P
Carpet 1 45.1 45.1 3.97 0.093 -> No hay diferencia entre las medias
Error 6 68.1 11.3
Total 7 113.1
S = 3.368 R-Sq = 39.85% R-Sq(adj) = 29.82%
Individual 95% CIs For Mean Based on
Pooled StDev
Level N Mean StDev ----+---------+---------+---------+-----
1 4 14.483 3.157 (----------*-----------)
2 4 9.735 3.566 (-----------*-----------)
----+---------+---------+---------+-----
7.0 10.5 14.0 17.5
Pooled StDev = 3.368
Tukey 95% Simultaneous Confidence Intervals
All Pairwise Comparisons among Levels of Carpet
Individual confidence level = 95.00%
Carpet = 1 subtracted from:
Carpet Lower Center Upper -+---------+---------+---------+--------
2 -10.574 -4.748 1.079 (-----------*----------)
-+---------+---------+---------+--------
-10.0 -5.0 0.0 5.0
131

132. ANOVA de un factor principal
y una variable de bloqueo
132

133. ANOVA – Prueba de hipótesis para
probar la igualdad de medias de
varias poblaciones con dos vías
Se trata de probar si el efecto de un factor o
Tratamiento en la respuesta de un proceso o sistema es
Significativo, al realizar experimentos variando
Los niveles de ese factor (Temp.1, Temp.2, etc.)
POR RENGLON
Y
Considerando los niveles de otro factor que se piensa
Que tiene influencia en la prueba – FACTOR DE BLOQUEO
POR COLUMNA
133

134. ANOVA – Prueba de hipótesis para
probar la igualdad de medias de
varias poblaciones con dos vías
Para el tratamiento – en renglones
Ho : 1  2  3  ......... a
Ha : A lg unas ' s.son.diferentes
.
Para el factor de bloqueo – en columnas
Ho :  '1   '2   '3  .........  'a
Ha : A lg unas ' s.son.diferentes
.
134

135. ANOVA 2 Factores - Ejemplo
Experiencia en años de los operadores
Maquinas 1 2 3 4 5
Maq 1 27 31 42 38 45
Maq 2 21 33 39 41 46
Maq 3 25 35 39 37 45
135

136. ANOVA – Dos factores, vías o
direcciones
 La SCT y SCTr (renlgones) se determina de la misma
forma que para la ANOVA de una dirección o factor
 En forma adicional se determina la suma de
cuadrados del factor de bloqueo (columnas) de forma
similar a la de los renglones
 La SCE = SCT – SCTr - SCBl
136

137. Tabla final ANOVA 2 Vías
FUENTE DE VARIACIÓN SUMA DE GRADOS DE CUADRADO VALOR F
CUADRADOS LIBERTAD MEDIO
Entre muestras (tratam.) SCTR a-1 CMTR CMTR/CME
Entre Bloques (Factor Bl) SCBl b-1 CMBL CMBL/CME
Dentro de muestras (error) SCE (a-1)(b-1) CME
Variación total SCT n-1 CMT
Regla: No rechazar si la F de la muestra es menor que la F de Excel para una cierta alfa
137

138. ANOVA – 2 Vías Toma de decisión
Distribución F Fexcel
Alfa
Zona de no rechazo de Ho Zona de rechazo
O de no aceptar Ha De Ho o aceptar Ha
Fc
Tr o Bl 138

139. ANOVA – 2 vías toma de decisión
Si Fc (Tr o Bl) es mayor que Fexcel se rechaza
Ho Aceptando Ha donde las medias son
diferentes
O si el valor de p correspondiente a Fc (Tr o Bl)
es menor de Alfa se rechaza Ho
139

140. Adecuación del modelo
 Los residuales o errores deben seguir una recta en la
gráfica normal
 Deben mostrar patrones aleatorios en las gráficas de
los residuos contra el orden de las Yij, contra los
valores estimados y contra los valores reales Yij
Residuales = eij = Yij (observada)–Yij (estimada)
140

141. Corrida en Minitab
 Se introducen las Zooplank- Supple-
respuestas en una ton ment Lake
columna C1 34 1 Rose
43 1 Rose
 Se introducen los 57 1 Dennison
subíndices de los 40 1 Dennison
renglones en una 85 2 Rose
columna C2 y de las 68 2 Rose
columnas en C3
67 2 Dennison
53 2 Dennison
141

142. Corrida en Minitab
 Opción: stat>ANOVA – Two Way (usar archivo
Exh_aov)
 En Response indicar la col. De Respuesta (Zooplant)
 En Row factor y Column Factor indicar las columnas
de subíndices de renglones y columnas (supplement
y lake) y Display Means para ambos casos
 Pedir gráfica residuales Normal Plot y vs fits y orden
142

143. Resultados
Two-way ANOVA: Zooplankton versus
Supplement, Lake
Source DF SS MS F P
Supplement 1 1225.13 1225.13 11.46 0.028
Lake 1 21.13 21.13 0.20 0.680
Interaction 1 351.13 351.13 3.29 0.144
Error 4 427.50 106.88
Total 7 2024.88
S = 10.34 R-Sq = 78.89% R-Sq(adj) = 63.05%
143

144. Pruebas de Hipótesis no
paramétricas para datos no normales
144

145. Pruebas de Hipótesis
Variables Atributos
No Normal Tablas de
Contingencia Chi Cuad.
Varianza Medianas
Correlación
Correlación
Homogeneidad Prueba de signos
de Varianzas
Wilcoxon
Normal Proporciones - Z
de Levene
Mann-
Whitney Variancia Medias
Kurskal-
Wallis 1- Población - Chi Pruebas Z, t
2- Pob. F 1- Población
Residuos
Prueba de Mood 2- Poblaciones
Homogeneidad distribuidos
Friedman de Varianzas ANOVA
de Bartlett Una vía normalmente
Dos vías
Correlación
Regresión 145

146. Resumen de pruebas de Hipótesis – Datos no normales
Pruebas de Varianzas
Homogeneidad de la varianza de Levine : Compara dos o
más varianzas de muestras de la misma población.
Pruebas de la Mediana
Prueba de signos: Prueba si el promedio de la mediana
de la muestra es igual a un valor conocido o a un valor a
alcanzar.
Prueba Wilcoxon: Prueba si la mediana de la muestra es
igual a un valor conocido o a un valor hipotético.
Prueba Mann-Whitney : Prueba si dos medianas de
muestras son iguales. 146

147. Resumen de pruebas de Hipótesis – Datos no normales
Pruebas de la Mediana
Prueba Kruskal-Wallis: Prueba si más de dos medianas
de muestras son iguales. Asume que todas las
distribuciones tienen la misma forma.
Prueba de la mediana de Mood: Otra prueba para más
de dos medianas. Prueba más firme para los valores
atípicos contenidos en la información.
Prueba de Friedman: Prueba si las medianas de las
muestras, clasificadas bajo dos categorías, son iguales.
Correlación: Prueba la relación lineal entre dos variables.
147

148. Tablas de contingencia
Prueba Chi 2 (2)
148

149. Ejemplo 2: Chi2 Para comparación de dos
grupos; ¿son las mismas proporciones?)
Ho: No existen diferencias en los índices de defectos de las dos máquinas
Ha: Existen diferencias en los índices de defectos de las dos máquinas.
Los valores observados (fo) son los siguientes:
Partes Partes
buenas defectuosas
máquina 1 fo = 517 f = 17 Total = 534
máquina 2 fo = 234 f = 11 Total = 245
779
Total 75128
El índice de defectos totales es 28 / 779 = 3.6%
149

150. Ejemplo 2: Chi2 Para comparación de dos
grupos; ¿son las mismas proporciones?)
Cálculo de los valores esperados
Partes buenas Partes defectuosas
máquina 1 fo = 751*534/779 fo = 28*534/779 Total = 534
máquina 2 fo = 751*245/779 fo = 28*245/779 Total = 245
779
Basados en este índice, los valores esperados (fe) serían:
Partes Partes defectuosas
buenas
máquina 1 530.53 3.47
máquina 2 233.47 1.53
150

151. Prueba de chi cuadrada:
Los conteos esperados están debajo de los conteos observados
Partes buenas Partes Defectuosas Total
1 532 2 534
530.53 3.47
2 232 3 235
233.47 1.53
Total 764 5 769
Chi2 = 0.004 + 0.624 + 0.009 + 1.418 = 2.056
DF= 1; valor de p = 0.152
2 celdas con conteos esperados menores a 5.0
151

152. Ejercicios
1. Se quiere evaluar si hay preferencia por manejar en un
carril de una autopista dependiendo de la hora del día. Los
datos se resumen a continuación:
Hora del día
Carril 1:00 3:00 5:00
Izquierdo 44 37 18
Central 28 50 72
Derecho 8 13 30
¿Con un 95% de confianza, existe una diferencia entre las
preferencias de los automovilistas dependiendo de la hora?
Ho: P1 = P2 = P3; Ha: al menos una es diferente
Grados de libertad = (columnas - 1) ( filas -1)

153. Ejemplo:
 Ejemplo:
Se cuestionó a veinte personas sobre cuánto tiempo
les tomaba estar listas para ir a trabajar, en las
mañanas. Sus respuestas (en minutos) se muestran
más adelante. ¿Cuáles son el promedio y la mediana
para esta muestra?
30, 37, 25, 35, 42, 35, 35, 47, 45, 60
39, 45, 30, 38, 35, 40, 44, 55, 47, 43
153

154. Un dibujo dice más que mil palabras
Promedio
Mediana
28.0 35.0 42.0 49.0 56.0 63.0
-------+---------+---------+---------+---------+---------+------ C1
Promedio = 40.35 Mediana = 39.5
El promedio puede estar influenciado considerablemente por los
valores atípicos porque, cuando se calcula un promedio, se incluyen los
valores reales de estos valores.
La mediana, por otra parte, asigna la misma importancia a todas las
observaciones, independientemente de los valores reales de los valores
atípicos, ya que es la que se encuentra en la posición media de los
valores ordenados.
154

155. Prueba de Signos de la Mediana
Para observaciones pareadas
Calificaciones de amas de casa a dos limpiadores de ventanas:
Ho: p = 0.5 no hay preferencia de A sobre B
Ha: p<>0.5
Ama Limpiador
Casa A B
1 10 7
2 7 5
¿Hay evidencia que indique
cierta preferencia de las amas
3 8 7
de casa por lo limpiadores?
4 5 2
5 7 6
6 9 6 155

156. Prueba de Signos de la Mediana
Producto
Familia A B Media = 0.5*n
1 - + Desv. Estand.= 0.5*raiz(n)
2 - +
3 + - Zc = (Y – media) / Desv. Estánd.
4 - + Rechazar Ho si Zc ><Zalfa/2
5 0 0
6 - +
7 - + ¿Hay evidencia que indique
8 + - cierta preferencia por un
9 - + Producto A o B?
10 - +
11 - +
156

157. Prueba de Signos de la Mediana
Media = 0.5*11 = 5.5
Desv. Estand.= 0.5*raiz(n) = 1.67
Para Zc = (8 – 5.5) / 1.67 = 1.497
Zexcel = 1.96 para alfa/2 = 0.025
Como Zc < Zexcel no se rechaza Ho o
Como p value = 0.067 > 0.025
No hay evidencia suficiente de que los
Consumidores prefieran al producto B
157

158. Prueba de Signos de la Mediana
Ejemplo (usando los datos del ejemplo anterior):
Ho: Valor de la mediana = 115.0
Ha: Valor de la mediana diferente de 115.0
N DEBAJO IGUAL ENCIMA VALOR P MEDIANA
29 12 0 17 0.4576 144.0
Ya que p >0.05, no se puede rechazar la hipótesis nula.
No se puede probar que la mediana real y la mediana hipotética son
diferentes.
En las páginas siguientes se muestra el detalle del cálculo.
158

159. Prueba de Signos de la Mediana
Ejemplo: Con los datos del ejemplo anterior y ordenándo de menor a
mayor se tiene: n = 29, Mediana de Ho = 115
No. Valor Signo No. Valor Signo No. Valor Signo
1 0 - 11 110 - 21 220 +
2 50 - 12 110 - 22 240 +
3 56 - 13 120 + 23 290 +
4 72 - 14 140 + 24 309 +
5 80 - 15 144 + 25 320 +
6 80 - 16 145 + 26 325 +
7 80 - 17 150 + 27 400 +
8 99 - 18 180 + 28 500 +
9 101 - 19 201 + 29 507 +
10 110 - 20 210 +
La mediana de los datos es 144. Si el valor contra el cual se
desea probar es 115, entonces hay 12 valores por debajo de el
(-) y 17 valores por arriba (+).
159

160. Prueba de Signos de la Mediana
Ho: Pi = 0.5 No hay preferencia
Ha: Pi <> 0.5 Hay preferencia
El estadístico X es el el número de veces que ocurre el signo menos
frecuente, en este caso el 12 (-).
Cómo n  25, se calcula el estadístico Z para la prueba de signos con:
Z = [ (Y + 0.5) - (0.5*n) / 0.5  n
En este caso Z1 = - 0.74278 y P(Z1) = 0.2288 para la cola izquierda
en forma similar P(Z2) = 0.2288 para la cola derecha, por lo que la
probabilidad total es 0.4576 >> 0.05 del criterio de rechazo.
Si n hubiera sido < 25 entonces se hubiera consultado la tabla de
valores críticos para la prueba de signo. 160

161. Prueba de Signos de la Mediana
¿Es esto correcto?¿144 podría ser igual a 115?
Bueno, veamos una gráfica de la información…
0 100 200 300 400 500
115 144
Después de todo, tal vez
esto SEA lo correcto.
161

162. Prueba de Mann-Whitney
Se llevó a cabo un estudio que analiza la frecuencia del
pulso en dos grupos de personas de edades
diferentes, después de diez minutos de ejercicios
aeróbicos.
Edad 40-44
Los datos resultantes se muestran a continuación. Edad 16-20
C1 C2
140 130
135 166
150 128
140 126
¿Tuvieron diferencias 144 140
154 136
significativas las frecuencias 160 132
de pulso de ambos grupos? 144 128
136 124
148
162

163. Prueba de Mann-Whitney
Edad 40-44 Edad 16-20
C1 C2
(7) 135 (1) 124
 Ordenando los datos (8.5) 136 (2) 126
y asignándoles el (11) 140 (3.5) 128
(rango) de su (11) 140 (3.5) 128
posición relativa se (13.5) 144 (5) 130
tiene (promediando (13.5) 144 (6) 132
(15) 148 (8.5) 136
posiciones para el
(16) 150 (11)140
caso de que sean (17) 154 (15)166
iguales): (18) 160
Ta y Tb suma de rangos n1 = 10 n2 = 9
Ta = 130.5 Tb = 55.5 163

164. Prueba de Mann-Whitney
Ho: Las distribuciones de frecuencias relativas de las poblaciones A y B son iguales
Ha: Las distribuciones de frecuencias relativas poblacionales no son idénticas
Ho: 1 = 2 Ha: 1  2 1, 2 = Medianas de las poblaciones
Ordenando los datos y asignándoles su posición relativa se tiene:
Ua = n1*n2 + (n1) * (n1 + 1) /2 - Ta
Ub = n1*n2 + (n2) * (n2 + 1) /2 - Tb
Ua + Ub = n1 * n2
Ua = 90 + 55 - 130.5 = 14.5 P(Ua) = 0.006 Ub = 90 + 45 - 55.5 = 79.5
El menor de los dos es Ua.
Para alfa = 0.05 el valor de Uo = 25
Como Ua < 25 se rechaza la Hipótesis Ho de que las medianas son iguales.
Dado que p < 0.05, rechazamos la hipótesis nula. Estadísticamente
existe una diferencia significativa entre los dos grupos de edad.
164

165. Prueba de Mann-Whitney
Ho: Las distribuciones de frecuencias relativas de las poblaciones A y B son iguales
Ha: Las distribuciones de frecuencias relativas poblacionales no son idénticas
Ua = 14.5 Ub = 79.5
Utilizando el estadístico Z y la distribución normal se tiene:
45 12.24
Z = [ (U - (n1* n2 / 2 ) / Raiz (n1 * n2 * (n1 + n2 + 1) / 12)
Con Ua y Ub se tiene:
Za = (14.5 - 45) / 12.24 = - 2.49 P(Z) = 0.0064 similar a la anterior
Zb = (79.5 -45) / 12.24 = 2.81 P(total) = 2 * 0.0064 = 0.0128 menor  = 0.05
El valor crítico de Z para alfa 0.025 por ser prueba de dos colas, es 1.96.
Como Za > Zcrítico se rechaza la Hipótesis Ho de que las medianas son iguales.
Dado que p < 0.05, rechazamos la hipótesis nula. Estadísticamente
existe una diferencia significativa entre los dos grupos de edad.
165

166. Prueba de Mann-Whitney
16-20 años de edad
130 166 128 126 140 136 132 128 124
140 10 -26 12 14 0 4 8 12 16
135 5 -31 7 9 -5 -1 3 7 11
40-44 años
150 20 -16 22 24 10 14 18 22 26
140 10 -26 12 14 0 4 8 12 16
de edad
144 14 -22 16 18 4 8 12 16 20
154 24 -12 26 28 14 18 22 26 30
160 30 -6 32 34 20 24 28 32 36
144 14 -22 16 18 4 8 12 16 20
136 6 -30 8 10 -4 0 4 8 12
148 18 -18 20 22 8 12 16 20 24
Diferencias entre los encabezados de los
renglones y las columnas
De esta manera, se calcula la mediana de todas estas diferencias, denominada "punto
estimado". Este punto estimado es una aproximación de la diferencia entre las medianas
de los dos grupos (ETA1 y ETA2).
Una vez ajustados los "enlaces" (eventos de un mismo valor en ambos grupos de
información), Minitab usa este punto estimado para calcular el valor p.
166

167. Prueba de Kruskal Wallis
Ordenando los datos de ventas y asignándoles el (rango) de su
posición relativa se tiene (promediando posiciones si son iguales):
Zona 1 Zona 2 Zona 3
(15.5) 147 (17.5) 160 (24) 215
(17.5) 17.5 (14) 140 (8) 127
(9) 128 (21) 173 (2) 98
(19) 162 (4) 113 (15.5) 127
(12) 135 (1) 85 (23) 184
(10) 132 (7) 120 (3) 109
(22) 181 (25) 285 (20) 169
(13) 138 (5) 117
(11) 133
(6) 119
n1 = 8 n2 = 10 n3 = 7 N = n1 + n2 + n3
Ta = 118 Tb = 111.5 Tc = 95.5 N = 25
167

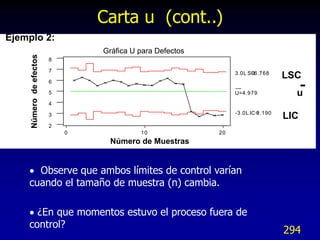
168. Prueba de Kruskal Wallis
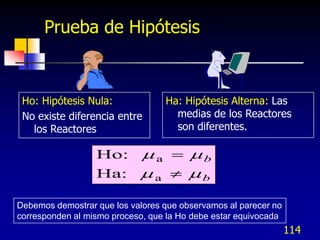
Ho: Las poblaciones A, B y C son iguales
Ha: Las poblaciones no son iguales
Ho: 1 = 2 = 3 Ha: 1  2  3 ; 1, 2, 3 =
Medianas de las poblaciones
Calculando el valor del estadístico H se tiene:
H = [ 12 /( N* ( N + 1)) ] * [ Ta2 / n1 + Tb2 / n2 + Tc2 / n3 ] - 3 * ( N +1 )
H = 0.01846 * (1740.5 + 1243.225 + 1302.893 ) - 78 = 1.138
Se compara con el estadístico 2 para  = 0.05 y G.l. = k - 1 = 3-1= 2
(k muestras)
2 crítico = 5.991 (válido siempre que las muestras tengan al menos 5
elementos)
Como H < 2 crítico, no se rechaza la Hipótesis Ho: Afirmando que no
hay diferencia entre las poblaciones 168

169. Coeficiente de correlación de
rangos para monotonía de
preferencias
Una persona interesada en adquirir un TV asigna
rangos a modelos de cada uno de 8 fabricantes
Rango
Fab. Preferencia Precio
Di
(rango) Di cuadrada
1 7 449.50 (1) 6 36
2 4 525.00 (5) -1 1
3 2 479.95 (3) -1 1
4 6 499.95 (4) 2 4
5 1 580.00 (8) -7 49
6 3 549.95 (7) -4 16
7 8 469.95 (2) 6 36
8 5 532.50 (6) -1 1 169

170. Coeficiente de correlación de
rangos para monotonía de
preferencias
Ho: No existe asociación entre los rangos
Ha: Existe asociación entre los rangos o es positiva o negativa
El coeficiente de correlación de rangos de Spearman es:
Rs = 1 – 6*suma(di cuadrada) / (n(n cuadrada – 1))
En este caso: Rs = 1 – 6(144)/(8*(64-1) = -0.714
R0 se determina de la tabla de Valores críticos del coeficiente de
correlación del coeficiente de correlación de rangos de
Spearman Rt = 0.686
170

171. Tabla de constantes
n Alfa=0.05 Alfa = 0.025
5 0.900 -
6 0.829 0.886
7 0.714 0.786
8 0.643 0.738
9 0.600 0.683
10 0.564 0.648
11 0.523 0.623
12 0.497 0.591
13 0.475 0.566
14 0.457 0.545
15 0.441 0.525
16 0.425 0.507
17 0.412 0.490
18 0.388 0.476
19 0.377 0.462
20 0.368 0.450
21 0.359 0.438
22 0.351 0.428
23 0.343 0.418
24 0.336 0.409
25 0.329 0.400
26 0.329 0.392
27 0.323 0.385
28 0.317 0.377
29 0.311 0.370
30 0.305 0.364 171

172. Salidas de la Fase de Análisis
 Causas raíz validadas
 Guía de oportunidades de mejora
172

173. Resumen de la validación de las causas
# de
Causa Causas Resultados Causa
Raíz
1 Ensamble de ojillos, bloques y SI ES CAUSA RAIZ X
contrapesos no adecuados en
aspas.
2 Amortiguadores dañados. SI ES CAUSA RAIZ X
3 Desgaste de bujes en los
carretes. NO ES CAUSA RAIZ
4 Fabricación y reemplazo de NO ES CAUSA RAIZ
ejes y poleas no adecuados en
ensamble de aspas.
Desalineamiento de poleas y
SI ES CAUSA RAIZ X
5 bandas de transmisión de
aspas.
Método de Balanceo no
6 SI ES CAUSA RAIZ X
adecuado.
7 Desalineación de pinolas en NO ES CAUSA RAIZ
cuna.
173

174. 8. Metodología Seis Sigma
Fase de Mejora
174

175. 8. Fase de Mejora
 Propósitos y salidas
 Diseño de experimentos
 Técnicas de creatividad
 Implantación y verificación de soluciones
175

176. Fase de mejora
 Propósito:
 Desarrollar, probar e implementar soluciones que atiendan a
las causas raíz
 Salidas
 Acciones planeadas y probadas que eliminen o reduzcan el
impacto de las causas raíz identificadas
 Comparaciones de la situación antes y después para
identificar la dimensión de la mejora, comparar los
resultados planeados (meta) contra lo alcanzado
176

177. FASE DE MEJORA
Causas
raíz Técnicas de
Diseño de creatividad
experimentos Tormenta de
ideas
Optimización Ideas Metodología
TRIZ
Efecto de X's Generación de soluciones
en las Y =
CTQs
Evaluación de soluciones
(Fact., ventajas, desventajas)
¿Solución
No factible?
Si
Implementación de
soluciones y verificación
de su efectivdad
Soluciones
verificadas
177

178. Diseño de Experimentos
(DOE)
178

179. Perspectiva histórica
 Ronald Fisher los desarrolla en su estación agrícola
experimental de Rothamsted en Londres (ANOVA)
1930
 Otros que han contribuido son: F. Yates, G.E.P. Box,
R.C. Bose, O. Kempthorne, W.G. Cochran, G. Taguchi
 Se ha aplicado el DOE en la agricultura y ciencias
biológicas, industria textil y lana, en los 1930’s
 Después de la II Guerra mundial se introdujeron en
la industria Química e industria electrónica
179

180. Introducción
 El cambiar un factor a un tiempo presenta las
desventajas siguientes:
 Se requieren demasiados experimentos para el estudio
 No se puede encontrar la combinación óptima de
variables
 No se puede determinar la interacción
 Se puede llegar a conclusiones erróneas
 Se puede perder tiempo en analizar las variables
equivocadas
180

181. ¿Por qué no probar un factor a la
vez?
TEMPERATURA TEMPERATURA
1 3
PRESION
PRESION
Zona Máxima Conclusión de la Prueba
2 4
PRESION
Optimo
PRESION
Respuesta Máxima
Conclusión de la Prueba
TEMPERATURA TEMPERATURA
181

182. Introducción
 El DOE varia varios factores simultáneamente de
forma que se puede identificar su efecto combinado
en forma económica:
 Se identifican los Factores que son significativos
 No es necesario un alto conocimiento estadístico
 Las conclusiones obtenidas son confiables
 Se pueden encontrar los mejores niveles de
factores controlables que inmunicen al proceso
contra variaciones en factores no controlables
182

183. ¿Qué es un diseño de
experimentos?
Cambios deliberados y sistemáticos de las variables de entrada
(factores) para observar los cambios correspondientes en la
salida (respuesta).
Entradas Salidas (Y) Entradas Salidas (Y)
Diseño de
Proceso
Producto
183

184. El Diseño de experimentos tiene
como objetivos determinar:
 Las X’s con mayor influencia en las Y’s
 Cuantifica los efectos de las principales X’s
incluyendo sus interacciones
 Produce una ecuación que cuantifica la relación entre
las X’s y las Y’s
 Se puede predecir la respuesta en función de cambios
en las variables de entrada
184

185. Principios básicos
 Obtención de réplicas: repetición del experimento (5
resultados en cada corrida expermental)
 Aleatorización: hacer en forma aleatoria:
 Permite confundir el efecto de los factores no controlables
 La asignación de los materiales utilizados en la
experimentación
 El orden en que se realizan los experimentos
185

186. Términos
 Error experimental
 Variación en respuesta bajo las mismas condiciones de
prueba. También se denomina error residual.
 Fraccional
 Un arreglo con menos experimentos que el arreglo
completo (1/2, ¼, etc.)
 Factorial completo
 Arreglo experimental que considera todas las
combinaciones de factores y niveles
 Interacción
 Ocurre cuando el efecto de un factor de entrada en la
respuesta depende del nivel de otro factor diferente
186

187. Términos
 Nivel
 Un valor específico para un factor controlable de
entrada
 Efecto principal
 Un estimado del efecto de un factor
independientemente del efecto de los demás
 Optimización
 Hallar las combinaciones de los factores que
maximizen o minimizen la respuesta
187

188. Factores y niveles
 Los factores son los elementos que cambian durante un
experimento para observar su impacto sobre la salida. Se
designan como A, B, C, etc.
- Los factores pueden ser cuantitativos o cualitativos
- Los niveles se designan como alto / bajo (-1, +1) o (1,2)
Factor
Factor Niveles cuantitativo, dos
B. Temp. de Moldeo 600º 700º niveles
E. Tipo de Material Nylon Acetal Factor cualitativo,
dos niveles
188

189. Pasos para Diseñar y Realizar un
Diseño de Experimentos
1. Observar datos históricos y/o recolectar datos para
establecer la capacidad actual del proceso debe estar
en control estadístico.
2. Determinar el objetivo del experimento (CTQs a
mejorar).
Por medio de un equipo de trabajo multidisciplinario
3. Determinar qué se va a medir como resultado del
experimento.
4. Identificar los factores de control y de ruido que
pueden afectar el resultado. 189

190. Pasos para Diseñar y Realizar un
Diseño de Experimentos
5. Determinar el número de niveles de cada factor y sus
valores reales.
6. Seleccionar un esquema experimental que acomode
los factores y niveles seleccionados y decidir el
número de replicas.
7. Verificar todos los sistemas de medición (R&R < 10%)
8. Planear y preparar los recursos
(gente, materiales, etc.) para llevar a cabo el
experimento. Hacer un plan de prueba.
190

191. Pasos para Diseñar y Realizar un
Diseño de Experimentos
9. Realizar el experimento, identificar muestras con la
condición experimental que la produce
• Medir las unidades experimentales.
11. Analizar los datos e identificar los factores
significativos.
12. Determinar la combinación de niveles de factores que
mejor alcance el objetivo.
191

192. Pasos para Diseñar y Realizar un
Diseño de Experimentos
13. Correr un experimento de confirmación con esta
combinación "óptima".
14. Asegurar que los mejores niveles para los factores
significativos se mantengan por largo tiempo mediante
la implementación de Procesos de Operación Estándar
y controles visuales.
15. Re evaluar la capacidad del proceso.
192

193. Ejemplo: Proceso de atención a clientes
en un Call Center
 Objetivos de los experimentos
 Caracterizar el proceso (identificar los factores que
influyen en la ocurrencia de errores)
 Optimizar, identificar el nivel óptimo de los factores
críticos para reducir el número de errores
 Identificar los factores controlables que pueden afectar
a la respuesta Y = Tiempo de solución de problema
 Identificar los factores de ruido que no podemos o
queremos controlar
193

194. Ejemplo: Proceso de atención a clientes
en un Call Center
 Variables de control X’s
 Número de líneas telefónicas
 Nivel del Personal
 Tiempo de acceso a bases de datos
 Horas laboradas al día
 Horas de atención
194

195. Ejemplo: Proceso de soldadura de una
tarjeta de circuito impreso
 Variables que no se pueden o desean controlar Z’s –
Variables de ruido
 Edad del ejecutivo de cuenta
 Distribución del Call Center
 Día del año
 Medio ambiente
 Horarios de comida
195

196. Los Factores Pueden Afectar...
1. La Variación del Resultado 3. La Variación y el Promedio
Con
Banda ancha
Entren.
Sin
Banda
entren.
angosta
Tiempo del servicio Tiempo del servicio
2. El Resultado Promedio 4. Ni la Variación ni el Promedio
Suficientes
ejectuvos Ambos sexos
Pocos ejecutivos
Toman el mismo
tiempo
Tiempo del servicio Tiempo del servicio
196

197. Tipos de Salidas
Las salidas se clasifican de acuerdo con nuestros objetivos.
Objetivo Ejemplos de Salidas
1. El Valor Meta es el Mejor
Lograr un • Tiempo de atención
valor meta con
variación mínima • Tiempo de conexión
Meta
2. El Valor Mínimo es el Mejor
Tendencia de • Tiempo de Ciclo
salida hacia cero
• Tiempo de
conexión
0
3. El Valor Máximo es el Mejor Tendencia de salida • Confiabilidad
hacia arriba
• Satisfacción
197

198. Respuesta de Salida Y =Tiempo de
La salida que se mide como resultado del experimento
y se usa para juzgar los efectos de los factores. conexión
Factores A. Tiempo de llamada
B. LOcalización
Las variables de entrada de proceso que se C. Experiencia
establecen a diferentes niveles para observar D. Tipo de Material usado
su efecto en la salida.
Factor (X’s) Niveles
Niveles A. Tiempo llamada 30 60 min.
Los valores en los que se establecen los factores. B. Localización 1 2
C. Experiencia 1 3
D. Material usado A B
Interacciones Experiencia x Material
El grado en que los factores dependen unos de otros. usado:
Algunos experimentos evalúan el efecto de las El mejor nivel de Material
depende de la experiencia.
interacciones; otros no.
Corridas A B C D Datos
Pruebas o Corridas Experimentales 1 -1 -1 -1 -1
Las combinaciones de pruebas específicas de factores y 2 -1 -1 + +1
1
niveles que se corren durante el experimento. 3 -1 +1 -1 +1
.
.
-1=Nivel Bajo
198
+1=Nivel Alto

199. Experimentos factoriales
completos 2K
199

200. Experimento factorial completo –
sin interacción
 Un experimento factorial completo es un experimento donde se
prueban todas las posibles combinaciones de los niveles de todos los
factores.
Factor A:
-1 +1
+1 30 52
Factor B: Y = Respuesta
-1 20 40
Efecto del factor A = (52+40)/2 - (30+20)/2 = 21
Efecto del factor B = (30+52)/2 - (20+40)/2 = 11
Efecto de A*B = (52+20)/2 – (30+40)/2 =1
200

201. Experimento sin interacción
B = +1 30 52
Respuesta
Promedio
B = -1 20 40
A = -1 A = +1
201

202. Experimento sin interacción
Respuesta
52
40
30
20
A = -1 A = +1
202

203. Modelo de regresión lineal
y   0  1 x1   2 x2  12 x1 x2
ˆ
  (20  40  30  52) / 4  35.5
0
ˆ
1  21/ 2  11
ˆ
 2  11/ 2  5.5
ˆ
12  1/ 2  0.5
y  35.5  10.5 x1  5.5 x2  0.5 x1 x2
ˆ
El coeficiente 0.5 es muy pequeño dado que no hay interacción
203

204. Gráfica de contornos – Experimentos
sin interacción
1 49 Dirección
De ascenso
46 rápido
.5 40
X2 34
0
28
-.5 22
-1
X1 -1 -.6 -.4 -.2 0.0 +.2 +.4 +.6 +.8 +1
204

205. Superficie de respuesta –
Experimentos sin interacción
Y = respuesta
Superficie de respuesta
Gráfica del modelo de regresión
X1
X2
205

206. Experimento factorial completo –
con interacción
 Un experimento factorial completo es un experimento donde se
prueban todas las posibles combinaciones de los niveles de todos los
factores.
Factor A = X1 :
-1 +1
+1 40 12
Y = Respuesta
Factor B = X2:
-1 20 50
Efecto de A*B = {(12+20)-(40+50)}/2 = -29
206

207. Experimento con interacción
B = +1 40 12
Respuesta
Promedio
B = -1 20 50
A = -1 A = +1
207

208. Modelo de regresión lineal
y   0  1 x1   2 x2  12 x1 x2
ˆ
  (20  40  30  52) / 4  30.5
0
ˆ
1  2 / 2  1
ˆ
 2  18 / 2  9
ˆ
12  58 / 2  29
y  30.5  1x1  9 x2  29 x1 x2
ˆ
El coeficiente -29 es muy grande representando la interacción
209

209. Gráfica de contornos
1 49 Dirección
De ascenso
25 43 rápido
.5
40
X2 31 34
0
28
-.5
-1
X1 -1 -.6 -.4 -.2 0.0 +.2 +.4 +.6 +.8 +1
210

210. Superficie de respuesta –
Experimentos con interacción
Superficie de respuesta
Gráfica del modelo de regresión
211

211. Experimento factorial con réplicas
 Un experimento factorial con réplicas tiene varios
resultados bajo la misma combinación de niveles
Factor A :
Horas entrenamiento
70 90
y1 y5
Factor B: 30’
Acceso al y2 Y6 Y = Tiempo de
sistema y3 y7 respuesta
60’
y4 y8
212

212. Análisis del efecto de la media
Factor A :
Horas de entrenam.
70 90
Factor B:
90 84
Acceso al 30 min.
87 87 Y = Tiempo de
sistema
95 79 conexión
60 min.
92 78
• ¿El tiempo de entrenamiento afecta el tiempo de conexión?
• ¿El tiempo de acceso afecta el tiempo de conexión?
• ¿Qué efecto tiene la interacción entre las horas de
entrenamiento y la hora del día sobre el tiempo de conexión?
213

213. El Efecto del entrenamiento
Factor B : Factor A : Horas de
Tiempo de entrenamiento
acceso
A1 = 70 A2 = 90
90 84
B1 = 30 min.
87 87
95 79
B2 = 60 min.
Tiempo de conexión
95
92 78 91
90
A1 = 90 + 87 + 95 + 92 = 91
85
82
4 80
84 + 87 + 79 + 78 = 82
A2 = 70 o
90
4
¿El tiempo de entrenamiento parece cambiar el
tiempo de conexión Y?
214

214. El Efecto del Tiempo de acceso
Factor B : Factor A : Horas de
Tiempo de entrenamiento
acceso
A1 = 70 A2 = 90
90 84
B1 = 30 min.
87 87
95 79
B2 = 60 min.
92 78 95
Tiempo de conexión
90 87
86
B1 = 90 + 87 + 84 + 87 = 87
85
4 80
95 + 92+ 79 + 78 = 86
B2 = 30 min. 60 min.
4
¿El cambio de tiempo de acceso parece cambiar
el tiempo de atención promedio del Call Center?
215

215. El Efecto de la Interacción
Factor A : Horas de entrenamiento
Factor B : Tiempo de
A1 = 70 o
A2 = 90 o
acceso
B1 = 30 90 84
min. 87 87
B2 = 60 95 79
Tiempo de conexión
min. 92 78 95
A1 A2 90
B1 88.5 85.5
85
B2 93.5 78.5 80
30 min. 60 min.
A,B, = 90 + 87 = 88.5
2
• En una gráfica de interacción, las líneas paralelas indican que no hay interacción. ¿Por qué?
• ¿Las horas de entrenamiento y el tiempo de acceso parecen interactuar?
• ¿Qué niveles de los factores deben usarse para reducir al mínimo la dureza de
las partes? 216

216. Corrida con Minitab – Creación del diseño
para 2 factores 2 niveles
Stat > DOE > Factorial > Create Factorial Design
o Two level
Designs: Number of center points 0
Number of Replicates 2
Number of blocks 1 OK
Options Non randomize runs OK
Factors Introducir el nombre real de los factores
y en forma opcional los niveles reales
Results Summary table, alias table OK
218

217. Corrida con Minitab – Diseño para 2
factores con 3 o más niveles
Stat > DOE > Factorial > Create Factorial Design
Type of Design: General Full Factorial
Designs: Number of levels 3, 3
Number of Replicates 2
Options Non randomize runs OK
Factors Introducir el nombre real de los factores
y en forma opcional los niveles reales
219

218. Corrida con Minitab – Análisis del
diseño factorial
 Hacer una columna de RESPUESTAS e introducir los datos
correspondientes a cada celda
Stat > DOE > Factorial > Analyze Factorial Design
Response Seleccionar la columna de las respuestas
Residuals Estandardized
Terms Pasar todos los términos a Selected con >> OK
Graphs Seleccionar Effects Plots Normal y Pareto
Seleccionar Residual plots: Normal y vs fits OK
Results Full table of fits and residuals
Seleccionar todos los términos con >> OK
OK
220

219. Corrida con Minitab –
Interpretación de gráficas
MAIN EFFECTS
 La gráfica de EFFECTS PLOT debe indicar fuera de la recta los
factores e interacciones que son significativas
 La gráfica EFFECTS PARETO debe indicar en sus barras
principales más allá de la recta de 0.1 o 0.05 los factores e
interacciones significativas
RESIDUALS
 La gráfica NORMAL PLOT de residuos debe mostrar los puntos
cerca de la recta
 La gráfica de residuos RESIDUALS vs FITS debe mostrar
aleatoriedad en los residuos
221

220. Corrida con Minitab –
Interpretación de resultados
Estimated Effects and Coefficients for Res (coded units)
Term Effect Coef SE Coef T P Variables significativas (p < 0.05, 0.1)
Constant 86.500 0.6614 130.78 0.000
A -9.000 -4.500 0.6614 -6.80 0.002
B -1.000 -0.500 0.6614 -0.76 0.492
A*B -6.000 -3.000 0.6614 -4.54 0.011
Modelo de regresión Y = 86.5 – 4.5 A – 3 AB (incluyendo sólo las variables significativas)
Analysis of Variance for Res (coded units)
Source DF Seq SS Adj SS Adj MS F P
Main Effects 2 164.00 164.00 82.000 23.43 0.006 Existencia del modelo
2-Way Interactions 1 72.00 72.00 72.000 20.57 0.011
Residual Error 4 14.00 14.00 3.500
Pure Error 4 14.00 14.00 3.500
Total 7 250.00
222

221. Tabla ANOVA – Experimento de
Tiempo de respuesta
Las horas de
Origen DF SS Sec SS Aj MS Aj F P entr. son
significativas.
Temp 1 162.000 162.00 162.00 46.29 0.002
El Tiempo de
Tiempo 1 2.000 2.000 2.000 0.57 0.492 acceso, no es
significativo.
Temp* 1 72.000 72.000 72.000 20.57 0.011
Tiempo
La interacción
Error 4 14.000 14.000 3.500 del tiempo de
acceso y horas
Total 7 250.000 de entr. es
significativa.
223

222. Corridas con Minitab – Gráficas
factoriales
Crear las gráficas factoriales y de interacción:
Stat > DOE > Factorial > Factorial Plots
Seleccionar Main effects e Interaction Plots
Setup para ambas: Seleccionar columna Respuesta
y con >> seleccionar todos los factores OK
Seleccionar Data Means OK
224

223. Interpretación de gráficas
 Si la interacción es significativa, entonces los mejores
niveles de operación del proceso ya sea para
maximizar o para minimizar la respuesta Y, se
seleccionan de la Gráfica de Interacción
 Si no es significativa la interacción, entonces los
mejores niveles de los factores se seleccionan de las
gráficas de efectos principales
225

224. Gráfica de efectos principales
Main Effects Plot (data means) for Res
-1 1 -1 1
90
88
Res
86
84
82
A B
226

225. Gráfica de interacciones
Interaction Plot (data means) for Res
A
-1
1
90
Mean
85
80
-1 1
B
227

226. Corridas con Minitab – Gráficas de
contorno y superficie de respuesta
Crear las gráficas de contorno y superficies de respuesta:
Stat > DOE > Factorial > Contour/Surface Plots
Seleccionar Contour / Surface Plots
Setup para ambas: Entrar a opción y dar OK
Seleccionar OK
228

227. Gráfica de contorno
Contour Plot of Res
1 82.5
85.0
87.5
90.0
92.5
0
B
-1
-1 0 1
A
Permite identificar la dirección de experimentación
de ascenso rápido perpendicular a los contornos
229

228. Gráfica superficie de respuesta
Surface Plot of Res
95
90
Res 85
80 1
0
-1
B
0 -1
A 1
230

229. Trayectoria de ascenso rápido
Respuesta
Pasos
231

230. Diseño central compuesto
Contour Plot of Y Surface Plot of Y
75
76
1
77
78 80.5
79 79.5
80 78.5
0
B
77.5
76.5
Y
75.5
74.5 1.5
1.0
-1 73.5 0.5
0.0
-1.5 -1.0
-0.5 B
-0.5 -1.0
0.0 0.5 -1.5
A 1.0 1.5
-1 0 1
A
Localización del punto óptimo
232

231. Diseño de Experimentos
de Taguchi
233

232. Diseño de experimentos de Taguchi
Sugiere tres pasos que son:
a) Diseño del sistema
b) Diseño de parámetros
c) Diseño de tolerancias
De estas tres etapas, la más importante es el diseño de
parámetros cuyos objetivos son:
a) Identificar qué factores afectan la característica de calidad en
cuanto a su magnitud y en cuanto a su variabilidad.
b) Definir los niveles “optimos” en que debe fijarse cada
parámetro o factor, a fin de optimizar la operación del
producto y hacerlo lo más robusto posible.
c) Identificar factores que no afecten substancialmente la
característica de calidad a fin de liberar el control de estos
factores y ahorrar costos de pruebas.
234

233. Taguchi ha desarrollado una serie de arreglos para experimentos con factores a dos niveles: La.
Número de condiciones Número de factores o efectos maximo
experimentales(renglones) que se pueden analizar y número de
lineas o pruebas. columnas
L4 4 3
L8 8 7
L12 12 11
L16 16 15
L32 32 31
L64 64 63
Ejemplo: En un proceso de formación de paneles, una característica no deseada es la emisión de
formaldehido en el producto final. Se cree que 5 factores pueden estar afectando la emisión, éstos son :
Factor Descripción Nivel I Nivel 2
A Tipo de resina Tipo I Tipo II
B Concentración 5% 10%
C Tiempo de ciclo de prensado 10 seg 15 seg
D Humedad 3% 5%
E Presión 800 psi. 900 psi.
Se desea analizar el efecto de cada factor y proponer las mejores condiciones de operación.
En este caso estamos interesados en analizar el efecto de 5 factores o efectos, a dos niveles cada
uno. Por lo tanto, se utilizará un arreglo ortogonal L8.
235

234. Se ejecutarán por lo tanto 8 pruebas o condiciones experimentales, ¿ A qué columna especificamente se
asignará cada factor?, en estos casos se pueden asignar a cualquier columna, aunque se recomienda
que aquellos factores que en la practica sea más dificil de variar de nivel continuamente, sean los
que se asigne a las primeras columnas.
El arreglo L8 y su descripción para este caso se muestra a continuación:
No. A B C D E e e Resina Concen. Tiempo Humedad Presión Yi
1 1 1 1 1 1 1 1 Tipo I 5% 10 seg. 3% 800 psi. 0.49
2 1 1 1 2 2 2 2 Tipo I 5% 10 seg. 5% 900 psi. 0.42
3 1 2 2 1 1 2 2 Tipo I 10% 15 seg. 3% 800 psi. 0.38
4 1 2 2 2 2 1 1 Tipo I 10% 15 seg. 5% 900 psi. 0.30
5 2 1 2 1 2 1 2 Tipo II 5% 15 seg. 3% 900 psi. 0.21
6 2 1 2 2 1 2 1 Tipo II 5% 15 seg. 5% 800 psi. 0.24
7 2 2 1 1 2 2 1 Tipo II 10% 10 seg. 3% 900 psi. 0.32
8 2 2 1 2 1 1 2 Tipo II 10% 10 seg. 5% 800 psi. 0.28
236

235. La tabla ANOVA es :
Efecto SS G.L. V Fexp. % Contrib.
A 0.03645 1 0.03645 58.32* 57.59
B 0.0008 1 0.0008 1.28 0.28
C 0.01805 1 0.01805 28.88** 28.01
D 0.0032 1 0.0032 5.12 4.14
E 0.00245 1 0.00245 3.92 2.93
Error 0.00125 2 0.000625 7.03
Total 0.0622 7 100
* significante al nivel 5% ya que F0.05 (1,2) = 18.51
** significante al nivel 10% ya que F0.10 (1,2) = 8.16
Nota : No se incluye en esta tabla específicamente la suma de cuadrados del promedio o
media. El error total es la suma de cuadrados total corregida por el factor de corrección.
Se acostumbra que aquellos efectos que no resultaron significantes, se consideren como error
aleatorio a fin de obtener una mejor estimación del error aleatorio, (con mayor número de
grados de libertad). 237

236. Gráficas lineales para el arreglo ortogonal L8
Columna 1 2 3 4 5 6 7
Col (1) 3 2 5 4 7 6
A Col (2) 1
Col (3)
6
7
7
6*
4
5
5
4
Col (4) 1 2 3
Col (5) 3 2
Col (6) 1
Col (7)
1
B 3 5 .7
4
2 6
2
3 C
5
1 4
6
7
238

237. A La matriz triangular las columnas están remarcadas, las interacciones forman la parte interior del
triangulo. Como ejemplo, sí asignamos el factor A en la columna 3 y el factor B en la columna 5, la
interacción AxB aparecerá en la en la intersección de las columnas, el número 6.
B En esta gráfica se observa el arreglo de tres factores ( 1,2 y 4) y la interacción entre ellos líneas 3,
5 y 6.
C En esta gráfica se indican cuatro factores (puntos 1,2,4 y 7) y las interacciones en las lineas 3, 5 y 6.
1 2 3 4 5 6 7
No. A B AXB D AxD AxC G
1 1 1 1 1 1 1 1
2 1 1 1 2 2 2 2
3 1 2 2 1 1 2 2
4 1 2 2 2 2 1 1
5 2 1 2 1 2 1 2
6 2 1 2 2 1 2 1
7 2 2 1 1 2 2 1
8 2 2 1 2 1 1 2
El arreglo ortogonal es exactamente el mismo, en este caso un L8.
239

238. Método Taguchi - Pasos
 Definir factores y niveles
 Factores de control (que se controlarán – arreglo interno)
 Factores de ruido (no se quieren o pueden controlar pero se
controlan durante el experimento – arreglo externo)
 Crear diseño de experimentos ortogonal de Taguchi
 Analizar el diseño de experimentos de Taguchi
 Predecir la respuesta con los niveles seleccionados
240

239. Método Taguchi – Crear Diseño
 Usar Stat / DOE / Taguchi / Create Taguchi Design para crear el
diseño ortogonal de Taguchi
 2 level Design, Number of factors (2 a 7) - 3
 Designs L8
 Factors (opcional para cambiar nombres de factores y
niveles; Assign columns of the array as specified below)
 Options Store designs in worksheet
 Ingresar al menos dos columnas de respuestas
241

240. Arreglo
Arregl Externo
o
Intern
o
A B C Resp1 Resp2
1 1 1 19.0 16.0
1 1 1 18.4 18.0
1 2 2 17.5 17.0
1 2 2 18.6 17.5
2 1 2 19.3 17.0
2 1 2 19.1 18.5
2 2 1 18.4 16.0
2 2 1 17.0 16.5 242

241. Método Taguchi – Analizar Diseño
 Usar Stat / DOE / Taguchi / Analize Taguchi Design para
analizar los resultados
 Response Data are in (al menos dos columnas de
respuestas)
 En Graphs seleccionar Signal to Noise Ratios, Means,
Estándar Deviations, Interaction Plots (pasar con >>)
 Display Interactions in Matrix o Separate Graph
 En Tables seleccionar Signal to Noise Ratios, Means,
Estándar Deviations
 En Options seleccionar Mayor es mejor, Nominal es mejor o
Menor es mejor para las relaciones Señal / Ruido, para que
en estas gráficas S/N se seleccionen los niveles que
maximicen la respuesta (para minimizar la variabilidad)
243

242. Response Table for Signal to Noise Ratios
Larger is better
Level A B C
1 24.9490 25.1379 24.7692
2 24.9302 24.7412 25.1099
Delta 0.0188 0.3967 0.3408
Rank 3 1 2
Response Table for Means
Level A B C
1 17.750 18.1625 17.4125
2 17.725 17.3125 18.0625
Delta 0.025 0.8500 0.6500
Rank 3 1 2
Response Table for Standard Deviations
Level A B C
1 0.98789 1.17022 1.16700
2 1.03722 0.85489 0.85810
Delta 0.04933 0.31533 0.30890
Rank 3 1 2
244

243. Main Effects Plot for Means Main Effects Plot for Standard Deviations
A B C A B C
18.2
1.17
18.0
1.09
17.8
StDev
Mean
1.01
17.6
0.93
17.4
0.85
1 2 1 2 1 2 1 2 1 2 1 2
Main Effects Plot for S/N Ratios
A B C
25.15
25.05
S/N Ratio
24.95
24.85
24.75
1 2 1 2 1 2
245

244. Método Taguchi – Predicción de
respuestas
 Usar Stat / DOE / Taguchi / Predict Taguchi Results para
predecir las respuestas en base a niveles de factores
seleccionados como óptimos
 Seleccionar Signal to Noise Ratios, Means, Estándar
Deviations
 En Terms pasar todos los términos con >>
 En Levels seleccionar Uncoded units (valores reales) o
Coded units (1 y 2) y Select levels from a list (niveles usados
 OK, se mostrarán las respuestas estimadas por concepto
246

245. Generación e implantación de
soluciones – Técnicas de
creatividad
247

246. Tormenta de ideas
 Permite obtener ideas de los participantes
248

247. SCAMPER
 Sustituir, Combinar, Adaptar, Modificar o ampliar,
Poner en otros usos, Eliminar, Revertir o re arreglar
Involucrar al cliente en el desarrollo del producto
 ¿qué procedimiento podemos sustituir por el actual?
 ¿cómo podemos combinar la entrada del cliente?
 ¿Qué podemos adaptar o copiar de alguien más?
 ¿Cómo podemos modificar nuestro proceso actual?
 ¿Qué podemos ampliar en nuestro proceso actual?
 ¿Cómo puede apoyarnos el cliente en otras áreas?
 ¿Qué podemos eliminar en la forma de inv. Del cliente?
 ¿qué arreglos podemos hacer al método actual? 249

248. Lista de atributos
 Lista de atributos: Dividir el problema en partes
 Lista de atributos para mejorar una linterna
Componente Atributo Ideas
Cuerpo Plástico Metal
Encendido/Apagado
Interruptor Encendido/Apagado
/luminosidad media
Batería Corriente Recargable
Bombillo de Vidrio Plástico
Peso Pesado Liviano
250

249. Análisis morfológico
 Conexiones morfológicas forzadas
Ejemplo: Mejora de un bolígrafo
Fuente de
Cilindrico Material Tapa
Tinta
De múltiples
Metal Tapa pegada Sin repuesto
caras
Cuadrado Vidrio Sin Tapa Permanente
En forma de Repuesto de
Madera Retráctil
cuentas papel
En forma de Tapa Repuesto
Papel
escultura desechable hecho de tinta
251

250. Los Seis Sombreros de pensamiento
 Dejemos los argumentos y propuestas y miremos
los datos y las cifras.
 Exponer una intuición sin tener que justificarla
 Juicio, lógica y cautela
 Mirar adelante hacia los resultados de una acción
propuesta
 Interesante, estímulos y cambios
 Visión global y del control del proceso
252

251. Dividir y analizar
 Dividir un problema en partes pequeñas y analizarlas por
separado: (Vendedor de pescado no ofrecía el sabor de pez
fresco)
 El Pez:
 Vive bajo el agua; tiene agallas; se mueve constantemente;
de sangre fria; cambia su color fuera del agua
 Solución:
 Se colocó un pequeño tiburón en la pecera para que el pez
conservara sus atributos vitales de frescura
253

252. Pensamiento forzado con palabras
aleatorias
 Crear nuevos patrones de pensamiento y forzar a ver
relaciones donde no las hay.
 Desarrollar ideas efectivas de lanzamiento de
productos: Impermeables
 Protegen de los elementos productos simples
 Son a prueba de agua productos laminados
 Son de hule flexibles flexibilidad de distribución
 Tienen bolsas productos de bolsillo
 Tienen capote publicidad amplia territorial
254

253. Listas de verificación
Haga Preguntas en base a las 5W – 1H.
 Por qué es esto necesario?
 Dónde debería hacerse?
 Cuándo debería hacerse?
 Quién lo haría?
 Qué debería hacerse?
 Cómo debería hacerse?
255

254. Mapas mentales
 Se inicia en el centro de una página con la idea
principal, y trabaja hacia afuera en todas direcciones,
produciendo una estructura creciente y organizada
compuesta de palabras e imágenes claves
 Organización; Palabras Clave; Asociación;
Agrupamiento
 Memoria Visual: Escriba las palabras clave, use colores,
símbolos, iconos, efectos 3D, flechas, grupos de palabras
resaltados.
 Enfoque: Todo Mapa Mental necesita un único centro.
256

255. TRIZ
 Hay tres grupos de métodos para resolver problemas
técnicos:
 Varios trucos (con referencia a una técnica)
 Métodos basados en utilizar los fenómenos y efectos
físicos (cambiando el estado de las propiedades físicas
de las substancias)
 Métodos complejos (combinación de trucos y física)
257

256. TRIZ – 40 herramientas
 Segmentación  Acción parcial o excesiva
 Extracción  Transición a una nueva dim.
 Calidad local  Vibración mecánica
 Asimetría  Acción periódica
 Continuidad de acción útil
 Combinación/Consolidación
 Apresurarse
 Universalidad
 Convertir lo dañino a benéfico
 Anidamiento  Construcción Neumática o
 Contrapeso hidráulica
 Contramedida previa  Membranas flexibles de capas
 Acción previa delgadas
 Compensación anticipada  Materiales porosos
258

257. TRIZ – 40 herramientas
 Equipotencialidad  Cambio de color
 Hacerlo al revés  Homogeneidad
 Retroalimentación  Rechazar o recuperar partes
 Mediador  Transformación de
 Autoservicio propiedades
 Copiado  Fase de transición
 Disposición  Expansión térmica
 Esferoidicidad  Oxidación acelerada
 Dinamicidad  Ambiente inerte
 Materiales compuestos
259

258. Generar y evaluar las soluciones
 Generar soluciones para eliminar la causa raíz o
mejora del diseño
 Probar en pequeño la efectividad de las soluciones
 Evaluar la factibilidad, ventajas y desventajas de las
diferentes soluciones
 Hacer un plan de implementación de las soluciones
(Gantt o 5W – 1H)
260

259. Implantación de soluciones
PUNTO CRITICO ACTIVIDADES
* Realizar las medidas como se habian acordado * Antes de aplicar las medidas correctivas
* Verificar si no hay efectos secundarios * Probar las ideas de mejora, investigar efectos
* Dar capacitacion y entrenamiento. secundarios que puedan afectar al producto o áreas*
Los equipos implantan las acciones correctivas y después poner en práctica las soluciones.
* Obtener la aprobación de las áreas relacionadas, turno o puesto, Jefe inmediato etc. Es decir,
Comunicar a todos los involucrados de la mejora a realizar.
EJEMPLO 1
LISTADO DE LAS MEDIDAS CORRECTIVAS
¿A QUE? - ¿COMO?
NO CUANDO DONDE RESU JUICIO QUIEN
TOPE PROC. DE LTAD
LIMPIEZA O
AUNQUE SE DA
BARRA DE EFECTO J. PÉREZ
1 JULIO 97 APLICACION NO ES PERSISTENTE
PARA LOS EXISTE POCO L.TORRES
2 JULIO 97 MOLDES DEFECTO
261

260. Implantación de soluciones
262
15 GUOQCSTORY.PPT

261. Verificación de soluciones
PUNTO CRITICO ACTIVIDADES
* Verificar hasta obtener efectos estables ampliando * Hacer análisis comparativo antes y después
los datos históricos en gráficas de la etapa de * En caso de aplicar varias medidas
correctivas
"razón de selección del tema" , Verificar los efectos intangibles sin omisiones
* Comparar el efecto en gráfica entre antes y después
de DMAIC respecto al objetivo. confirmar el efecto sobre cada concepto de
(relación humana, capacidad, trabajo en equipo, contramedidas.
entusiasmo, área de trabajo alegre).
* Determinar los beneficios monetarios, indirectos e intangibles.Investigar si existen áreas y operaciones
similares tanto dentro como fuera de la planta, para aplicar las mismas contramedidas. Dar reconocimiento.
Ejemplo 1.
% 2.5
2.33
D 2.19
2.1 2.14
2.22 %D < 1 %
2
E
2
1.9
1.8 1.76
F 1.5
1.7
1.6
1.5
E 1.32
1.4
1.3
1.2
C 1 0.9 0.94
1.1
1
0.99 0.94
0.87
T 0.79
U 0.5
S
O
0
May-97 Jun-97 Jul-97 Ago-97 S ep-97 Oct-97 Nov-97 Dic-97 Ene-98 Feb-98 Mzo-98 263
Abr-98

262. 9. Metodología Seis Sigma
Fase de Control
264

263. 9. Fase de Control
 Propósitos y salidas
 Plan de control
 Control estadístico del proceso
 Técnicas Lean
265

264. Fase de Control
 Objetivos:
 Mantener las mejoras por medio de control estadístico
de procesos, Poka Yokes y trabajo estandarizado
 Anticipar mejoras futuras y preservar las lecciones
aprendidas de este esfuerzo
 Salidas:
 Plan de control y métodos de control implementados
 Capacitación en los nuevos métodos
 Documentación completa y comunicación de
resultados, lecciones aprendidas y recomendaciones
266

265. FASE DE CONTROL
Soluciones
implementadas
Plan de Documentar
Control Estándares y Capacitar
CEP - de trabajo
Herramientas
Poka Yokes Lean
Plan de calidad y Monitoreo
Si ¿Proceso
en control?
No
Tomar acciones correctivas
y preventivas -
Actualizar AMEF
267

266. Prototype
Control Plan Number
Part Number/Latest Change Level
Pre- launc h Produc tion
CONTROL PLAN
Key Contac /Phone
Core Team
Date (Orig.)
Customer Engineering Approval/Date (if Req'd.)
Page
Date (Rev.)
of
Plan de control
Part Name/Desc ription Supplier/Plant Approval/Date Customer Quality Approval/Date (if Req'd.)
Supplier/Plant Supplier Code Other Approval/Date (if Req'd.) Other Approval/Date (if Req'd.)
Part / Proc ess Name / Mac hine, Devic e, Charac teristic s Spec ial Methods
Proc ess Operation Jig, Tools Char.
Number Desc ription For Mfg. No. Produc t Proc ess Class. Produc t/Proc ess Evaluation/ Sample Control Method Reac tion Plan
- Todos los procesos
Spec ific ation/ Measurement Size Freq.
Toleranc e Tec hnique
- Todas las Operaciones
- Todas las actividades
Hoja de Instrucción calidad
No de Producto Dibujo No. Operación No. Maquína Elaboró Aprobó
Nombre del producto Nivel
Caracteristica Especificación Criterio Instrumento Tamaño Frecuenc. Método de Plan de Reacción
Descripción & Tolerancia d´muestra Registro
- Un proceso
- Una actividad
- Operaciones Limitadas Operador
Ayuda Visual
Instrucciones:
Distribución
268

267. CEP objetivos y beneficios
 El CEP es una técnica que permite aplicar el análisis
estadístico para medir, monitorear y controlar
procesos por medio de cartas de control
 Se basa en que los procesos presentan variación,
aleatoria y asignable
 Entre los beneficios se encuentran:
 Monitorear procesos estables e identificar si han
ocurrido cambios debido a causas asignables para
eliminar sus fuentes
269

268. CEP por variables y atributos
 El CEP por variables implica realizar mediciones en la
característica de calidad de interés, tal como:
 Tiempos
 Velocidad
 El CEP por atributos califica a los productos como
buenos / defectivos o por cuantos defectos tienen:
 Color, funcionalidad, apariencia, etc.
270

269. ¿Qué es una Carta de Control?
 Una Carta de Control es como un historial del proceso...
... En donde ha estado.
... En donde se encuentra.
... Hacia donde se puede dirigir
 Las cartas de control pueden reconocer cambios buenos y
malos.
¿Qué tanto se ha mejorado?
¿Se ha hecho algo mal?
 Las cartas de control detectan la variación anormal en un
proceso, denominadas “causas especiales o asignables de
variación.”
271

270. Variación observada
en una Carta de Control
 Una Carta de control es simplemente un registro de
datos en el tiempo con límites de control superior e
inferior, diferentes a los límites de especificación.
 El patrón normal de un proceso se llama causas de
variación comunes.
 El patrón anormal debido a eventos especiales se
llama causa especial de variación.
272

271. Variación – Causas comunes
Límite
inf. de
especs.
Límite
sup. de
especs.
Objetivo
273

272. Variación – Causas especiales
Límite
inf. de
especs.
Límite
sup. de
especs.
Objetivo
274

273. Patrones de anormalidad
en la carta de control
“Escuche la Voz del Proceso” Región de control,
M captura la variación
E
natural del proceso
D
I original
D LSC
A
S
C
A LIC
L Tendencia del proceso
I
D El proceso ha cambiado
A
Causa Especial
identifcada
D
TIEMPO
275

274. Cartas de Control para
variables
276

275. Cartas de Control por Variables
 Medias Rangos (subgrupos de 5 - 9 partes cada x
horas, para estabilizar procesos)
 Medianas Rangos (para monitorear procesos
estables)
 Valores Individuales (partes individuales cada x
horas, para monitoreo de procesos muy lentos o
químicos)
277

276. Implantación de cartas
de control por variables
1. Identificar la característica a controlar en base a un
AMEF (análisis del modo y efecto de falla)
2. Establecer métodos, muestras y frecuencia
3. Validar la habilidad del sistema de medición R&R
4. Centrar el proceso, correrlo y medir al menos 25
subgrupos de 5 partes cada uno, calcular límites
5. Identificar causas especiales, prevenir su recurrencia,
recalcular límites y continuar control para reducir causas
comunes
278

277. Carta X, R (Continuación)
Terminología
k = número de subgrupos; n = número de muestras en cada subgrupo
X = promedio para un subgrupo
X = promedio de todos los promedios de los subgrupos
R = rango de un subgrupo
R = promedio de todos los rangos de los subgrupos
x1 + x2 + x3 + ...+ xN
x =
n
x1 + x2 + x3 + ...+ xN
x =
k
LSCX = x + A2 R NOTA: Los factores a considerar
LICX = x - A2 R para n = 5
LSCR = D4 R Son A2 = 0.577 D3 = 0 D4 = 2.114
LICR = D3 R 279

278. Ejemplo de carta de control X-R
Xbar-R Chart of Pulse1
90
U C L=86.84
Sample Mean
80
_
_
X=72.69
70
60
LC L=58.53
2 4 6 8 10 12 14 16 18
Sample
U C L=51.89
48
Sample Range
36
_
24 R=24.54
12
0 LC L=0
2 4 6 8 10 12 14 16 18
Sample
280

279. Carta de Individuales (I-MR)
 Esta Carta monitorea la tendencia de un proceso con
datos variables que no pueden ser muestrados en lotes o
grupos.
 Este es el caso cuando la capacidad de
corto plazo se basa en subgrupos racionales de una unidad
 La línea central se basa en el promedio de los datos, y
los límites de control se basan en la desviación estándar
poblacional (+/- 3 sigmas)
281

280. Carta X, R (Continuación)
Terminología
k = número de piezas
n = 2 para calcular los rangos
x = promedio de los datos
R = rango de un subgrupo de dos piezas consecutivas
R = promedio de los (n - 1) rangos
x1 + x2 + x3 + ...+ xN
x =
n
n 2
LSCX = x + E2 R D4 3.27
LICX = x - E2 R D3 0
LSCR = D4 R E2 2.66
LICR = D3 R
(usar estos factores para calcular Límites de Control n = 2) 282

281. Ejemplo: Carta I-MR
I-MR Chart of Pulse2
150
1
1
Individual Value
125 1 1
1 1
U C L=113.2
100
_
X=80
75
50 LC L=46.8
1 9 18 27 36 45 54 63 72 81 90
O bser vation
1
60
Moving Range
1
45 1
U C L=40.75
30
15 __
M R=12.47
0 LC L=0
1 9 18 27 36 45 54 63 72 81 90
O bser vation
Observar las situaciones fuera de control 283

282. Cartas de Control
para atributos
284

283. Cartas de control para atributos
Datos de Atributos
Tipo Medición ¿Tamaño de Muestra ?
p Fracción de servicios erroneos, Constante o variable > 30
defectivos o no conformes
np Número de servicios erroneos Constante > 30
c Número de defectos, errores o Constante = 1 Unidad de
no conformidades inspección
u Número de defectos por unidad Constante o variable en
unidades de inspección
285

284. Cartas de Control tipo p
 p - CON LÍMITES DE CONTROL VARIABLES
 p - CON n PROMEDIO
 p - ESTANDARIZADA
286

285. Carta p (Cont..)
Ejemplo:
Gráfica P para Fracción Defectiva
0.5
0.4
3.0SL= 0.4484 LSC
Proporci
0.3
ón
0.2
0.1 P= 0.1128 p
0.0 -3.0SL= 0.000
LIC
0 5 10
Número de muestra
 Observe como el LSC varía conforme el tamaño (n) de cada
muestra varía.
 Los límites de control se pueden estabilizar con n promedio o
estandarizando pi con Zi.
287

286. Carta np (Atributos)
 Se usa cuando se califica al servicio como bueno/malo, pasa/no
pasa.
 Monitorea el número de servicios erronoes de una muestra
 El tamaño de muestra (n) es constante y mayor a 30.
Terminología (igual a gráfica p, aunque n es constante)
n = tamaño de cada muestra (Ejemplo: servicios diarios)
np = número de servicios erroneos en cada muestra
k = número de muestras
288

287. Carta np (Cont...)
Ejemplo 1:
Carta np de número de servicios erroneos
10 3.0 LSC=10.03
No. De fecetivos
5
Np =4.018 np
0 - 3.0S LIC=0.0 LIC
0 5 10 15
Número de muestras
 El tamaño de la muestra (n) es constante
 Los límites de control LSC y LIC son constantes
 Evita hacer cálculos al presatdor del servicio
289

288. Cartas de Control para
defectos o errores
c – Número de defectos
Se cuentan los defectos que tienen cada
unidad de inspección de tamaño n
constante en productos como facturas
u – Defectos por unidad
Se cuentan los defectos que tienen
diferentes unidades de inspección de
tamaño n variable en productos
complejos y se determinan los defectos
por unidad – Facturas
290

289. Carta c (Atributos)
 El tamaño de la muestra (n unidades de inspección)
debe ser constante
 Ejemplos:
- Número de errores en cada lote de facturas
- Número de cantidades ordenadas incorrectas en
órdenes de compra
Terminología
c = Número de defectos encontrados en cada
unidad o unidades constantes de inspección
k = número de muestras
291

290. Carta c (cont..)
Ejemplo:
Carta C
15 1
Número de defectos
3.0L SC12.76
= LSC
10
5 C = 5.640 C
0 -3.0L IC=
0.000
0 5 10 15 20 25
Número de Muestras
 Observe el valor de la última muestra; está fuera del límite
superior de control (LSC)
 ¿Qué información, anterior a la última muestra, debió haber
obviado el hecho de que el proceso iba a salir de control?
292

291. Carta u (Atributos)
 El tamaño de la muestra (n) puede variar
 Los defectos o errores por unidad se determinan dividiendo el
número de defectos encontrados en la muestra entre el número
de unidades de inspección incluidas en la muestra (DPU o
número de defectos por unidad) .
 Ejemplos:
• Se toma una muestra de facturas por semana, identificando
los errores en estas.
• Se inspeccionan servicios prestados por día, se determinan
los errores promedio por día.
293

292. Carta u (cont..)
Ejemplo 2:
Gráfica U para Defectos
Número de efectos
8
7 3.0L SC
=6.768
LSC
6
5 U=4.979 u
4
-3.0L IC=
3.190
3 LIC
2
0 10 20
Número de Muestras
 Observe que ambos límites de control varían
cuando el tamaño de muestra (n) cambia.
 ¿En que momentos estuvo el proceso fuera de
control?
294

293. Cartas de Precontrol
295

294. Cartas de precontrol (Shainin)
 Es más exitosa con procesos estables no sujetos a
corridas rápidas una vez que se implementan y
estabilizan
 Sirven como referencia y monitoreo
 La distancia entre los límites de especificaciones o
tolerancias se divide entre cuatro quedando los
límites de control entre el primer y tercer cuarto
296

295. Pre- Control
Bajo Alto
Línea Línea
P-C P-C
Rojo Amarillo Verde Amarillo Rojo
1/4 1/2 1/4
Tolerancia Completa
297

296. Reglas de Precontrol
Tomar una muestra de dos servicios consecutivos A y B:
1. Sí A y B caen en verde, continuar el proceso
2. Sí A es amarilla y B cae en verde continuar proceso.
3. Sí A y B son amarillas investigar causas en el proceso
4. Sí A o B son rojas, parar proceso e investigar causas
298

297. Acciones a tomar
Ultima servicio Servicio actual
Verde Continuar
Amarillo Primera: Continuar
Segunda: Detener
Rojo Detener
299

298. Distribución de probabilidad
LI Espec. Línea Línea LS Espec.
P-C P-C
1/14 12/14 1/14
7% 86% 7%
Rojo Amarillo Verde Amarillo Rojo
Area Objetivo
1/4 1/2 1/4
Tolerancia Completa
300

299. Estandarización
1. Controles para la mejora.
2. Formas para eliminar causas.
3. Datos de control de resultados.
4. Aplicación de soluciones en otros
procesos.
5. Uso de métodos de estandarización.
. 301

300. Prevención de la reincidencia –
Estandarización
DISPOSITIVOS A PRUEBA DE ERROR ( Poka - Yokes ).
302
22 GUOQCSTORY.PPT

301. 10. Empresa Lean
303

302. Métodos Lean
 Pensamiento Lean, Muda
 Fábrica visual
 5S’s (Organización del lugar de trabajo)
 Kaizen
 Kanban
 Teoría de restricciones
 Poka Yokes
 Estándares de trabajo
 SMED
 TPM 304

303. Pensamiento Lean
 Womack (1990) introduce el término de producción
Lean en occidente en 1990 con la su libro “The
machine that changed the World”, describe las
prácticas de las mejores empresas en el mundo:
 Especificar el valor por producto
 Identificar la cadena de valor para cada producto
 Identificar el flujo de valor
 Permitir que el cliente jale valor del proveedor
 Perseguir la perfección
305

304. Muda, los 7 desperdicios
 El Muda son actividades que no agregan valor en el
lugar de trabajo. Su eliminación es esencial para
reducir costos y tener calidad en producto:
 Recursos en exceso
 Inventarios
 Reparaciones / Retrabajos
 Movimientos
 Proceso de firmas
 Esperas
 Transportes
306

305. Pensamiento Lean
 Cadenas de valor: La reducción del desperdicio se
concentran en 3 actividades clave de procesos:
 Desarrollo de nuevos productos: definir el concepto,
diseño y desarrollo del prototipo, revisión de planes y
mecanismo de lanzamiento
 Gestión de información: toma de pedidos, compra de
materiales, programación interna y envió al cliente
 Transformación: realización del producto o servicio
desde inicio hasta fin
307

306. Reducción de tiempo de ciclo
 El tiempo de ciclo es la cantidad de tiempo necesaria
para completar una actividad del proceso, un evento
Kaizen Blits puede reducirlo a ser menor al Takt time
 Beneficios:
 Satisfacer al cliente
 Reducir gasto interno y externo
 Incrementar la capacidad
 Simplificar la operación y actividad
 Continuar siendo competitivo
308

307. Administración visual
 Tiene como propósito mostrar a la administración y
empleados lo que está sucediendo en cualquier
momento de un vistazo
 Uso de pizarrones o pantallas para mostrar el estado
de:
 La prestación de servicios
 Los programas
 La calidad del servicio
 Los tiempos de entrega
 Requerimientos del cliente y costos
309

308. 5S’s
 Seiko (arreglo adecuado)
 Seiton (orden)
 Seiketso (limpieza personal)
 Seiso (limpieza)
 Shitsuke (disciplina personal)
 En Inglés:
 Sort (eliminar lo innecesario)
 Straighten (poner cada cosa en su lugar)
 Scrub / Shine (limpiar todo
 Systematize (hacer de la limpieza una rutina)
 Standardize (mantener lo anterior y mejorarlo) 310

309. Kaizen Blitz (evento o taller)
 Involucra una actividad Kaizen (proyecto de mejora)
en un área específica por medio de un equipo de
trabajo durante 3 a 5 días:
 2 días de entrenamiento
 3 días para colección de datos, análisis e
implementación de la solución
 Es necesario el apoyo de la administración
 Al final el equipo hace una presentación del
proyecto
311

310. Kaizen Blitz (evento o taller)
 Resultados:
 Ahorro de espacio
 Flexibilidad de atención al cliente
 Flujo de trabajo mejorado
 Ideas de mejora
 Mejoras en calidad
 Ambiente de trabajo seguro
 Reducción de actividades que no agregan valor
312

311. Kanban
 Kanban = signo. Es una señal a los procesos internos
para proporcionar servicios (tarjetas, banderas,
espacio en el piso, etc.). Da indicación visual de:
 Números, código de barras
 Cantidad
 Localización
 Tiempo de entrega
 Colores en función del destino
313

312. Teoría de restricciones
 Goldratt (1986) escribe “La Meta” describiendo un
proceso de mejora continua
 La Gestión de restricciones se enfoca a remover los
cuellos de botella del proceso que limita el throughput
 Las restricciones pueden hallarse con un mapa del
proceso, diagrama PDPC y Diagrama de árbol
314

313. Teoría de restricciones
 Las métricas básicas son:
 Throughput: es la tasa a la cual el sistema genera
dinero a través de las ventas. Dinero que ingresa.
 Inventarios: es todo el dinero invertido en el sistema
en cosas compradas para vender. Dinero utilizado.
 Costos de operación: es el dinero que el sistema usa
para transformar el inventario en throughput. Dinero
que sale.
315

314. Teoría de restricciones
 Otras definiciones:
 Los Recursos Cuello de botella tienen una capacidad
menor o igual que la demanda asignada a estos.
 El balance de flujo de prestación del servicio debe ser
hecho contra la demanda del cliente.
316

315. Teoría de restricciones- Método
de cinco Pasos
 Identificar las restricciones del sistema que limitan el
logro de objetivos, darles prioridad por su impacto
 Decidir como explotar las restricciones del sistema.
Asignarles los recursos sobrantes de otras áreas
 Subordinar cada cosa a las decisiones anteriores.
Reducir el efecto de la restricción o expandir su
capacidad
317

316. Teoría de restricciones- Método
de cinco Pasos
 Elevar las restricciones del sistema, tratar de eliminar
los problemas de la restricción, hacer esfuerzos para
continuar las mejoras
 Regresar al primer paso después de romper las
restricciones, buscar otras nuevas
318

317. Teoría de restricciones
 Evaporando nubes:
 Frecuentemente existen soluciones simples para problemas
complejos, reexaminar los fundamentos del problema
 Árboles de prerrequisitos:
 Algo debe ocurrir antes de que algo adicional ocurra. La T.R.
Permite la transición entre la forma anterior de hacer las
cosas y la nueva forma
319

318. Poka Yoke
 Con dispositivos sencillos a Prueba de error se
pueden evitar los errores humanos por:
 Olvidos
 Malos entendidos
 Identificación errónea
 Falta de entrenamiento
 Distracciones
 Omisión de las reglas
 Falta de estándares escritos o visuales
320

319. Poka Yoke
 Beneficios
 No requiere entrenamiento formal
 Elimina muchas operaciones de inspección
 Proporciona un 100% de inspección interna sin fatiga o
error humano.
 Contribuye al trabajo libre de defectos
321

320. Poka Yokes
 Se puede lograr a prueba de error por medio de un
control para prevenir errores humanos o usando
mecanismos de alerta.
 Para prevenir errores humanos se tienen:
 Diseño de métodos para evitar errores
 Uso de dispositivos que no soporten una actividad mal
realizada
 Teniendo procedimiento de trabajo controlado por
dispositivos a prueba de error
322

321. Poka Yokes
 Los mecanismos de alerta de errores incluyen:
 Uso de colores
 Formatos guía para facilidad de llenado
 Mecanismos para detectar el proceso de información
equivocada
 Una alarma indica que ha ocurrido un error y se debe
atender de inmediato
 Se pueden combinar los Poka Yokes para obtener cero
defectos con: inspecciones en la fuente,
autoinspecciones por el ejecutivo y métodos de
inspección sucesivos (Shingo)
323

322. Estándares de Trabajo
 Documentan la mejor manera de hacer el trabajo, en
forma más fácil y segura.
 Preservan el Know How y experiencia para hacer el
trabajo que puede perderse al irse los empleados
 Proporcionar un método de evaluar el desempeño
 Proporcionan una base para mantenimiento y mejora
 Son la base de la capacitación y auditoria
 Método para prevenir la recurrencia de errores
 Minimizan la variabilidad 324

323. Estándar de trabajo
 Las hojas de estándares de trabajo combinan
elementos de materiales, personas y equipos en un
ambiente de trabajo, consideran lo siguiente:
 Disponibilidad de recursos
 Distribución de equipos
 Mejoras al proceso y sistemas autónomos instalados
 Valuación de ideas del personal
 Minimización de transporte
 Optimización de l inventario
 Prevención de defectos
 Conceptos de área de trabajo segura
325

324. Otros Estándares de Trabajo
 Líneas amarillas en el piso
 Códigos de colores
 Pizarrón de control para desarrollo de los servicios
 Indicadores de nivel mínimo y máximo de inventarios
 Matrices de capacitación cruzada
 Lámparas de falla
326

325. SMED
 Single Minute Exchange of Die SMED se enfoca a
reducir los tiempos de preparación y ajuste de horas
a minutos.
 Mitos en relación con los ajustes y preparaciones:
 La habilidad para hacer preparaciones se gana con la
práctica y la experiencia
327

326. SMED - Pasos
 Formación de un equipo de trabajo con personal
involucrado en el servicio
 Primer paso, observar las condiciones actuales por
medio de:
 Uso de cronómetro para observación continua
 Uso de un estudio de trabajo por muestreo
 Entrevistas de ejecutivos
 Videofilmación de la operación completa
 División de los pasos del proceso de preparación en
partes más pequeñas y clasificación en preparación
interna (equipos parados) o externa (trabajando)
328

327. SMED - Pasos
 Las operaciones de preparación externa incluyen:
 Preparación de información
 Búsqueda de información
 Evaluación de parámetros
 Etc...
 Después reexaminar los elementos internos y
externos y tratar de convertir los más que se puedan
a externos, utilizar la creatividad del equipo
329

328. TPM
 El mantenimiento productivo total incluye la
participación de todos para asegurar la disponibilidad
del equipo de producción y combina los
mantenimientos preventivo, predictivo, mejoras en la
mantenabilidad, facilidad de mantenimiento y
confiabilidad
330

329. TPM
 Hay 6 grandes pérdidas que contribuyen en forma
negativa a la efectividad del equipo:
 Falla del equipo
 Preparación y ajustes
 Arranques y paros menores
 Velocidad reducida
 Defectos de proceso
 Pérdidas de producto
331

330. Implementación del TPM
 Pasos recomendados para implementar el TPM:
 Anunciar el compromiso de la dirección al TPM
 Campaña educacional sobre TPM en la empresa
 Organizar equipos para promover el TPM
 Establecer metas y políticas para el TPM
 Preparar un plan detallado para el TPM
 Junta directiva de arranque (kick off) del TPM
 Formar equipos de mejora de la efectividad del equipo
 Desarrollar a los operadores para mantto. Autónomo
 Desarrollar un programa de mantenimiento de equipo
 Capacitar a operadores y gente de mantenimiento
 Desarrollar programas de mantto. Para el equipo nuevo
 Tener implementado el TPM y buscar la perfección332

331. Mantenimiento autónomo
 Actividades de grupos pequeños autónomos para TPM:
 El supervisor es el líder del equipo
 Realizan actividades de limpieza, lubricación,
protecciones, inspección, etc.
 Evolución de los equipos:
 Auto desarrollo: aprendizaje de los miembros
 Actividades de mejora: terminadas
 Solución de problemas: selectos
 Administración autónoma: selecciona sus metas y
administran su trabajo
333

332. TPM
 Diseño para mantenabilidad y disponibilidad:
 Estandarización: minimizar el número de partes
diferentes
 Modularización: estandarizar tamaños, formas, unidades
 Accesibilidad: facilitar las tareas de mantto. Y acceso
 Alarma por mal funcionamiento: luces o sonido
 Aislamiento de falla: equipo de autoprueba,
mantenimiento preventivo, simplicidad en diseño
 Identificación: única de componentes y bitácoras
334