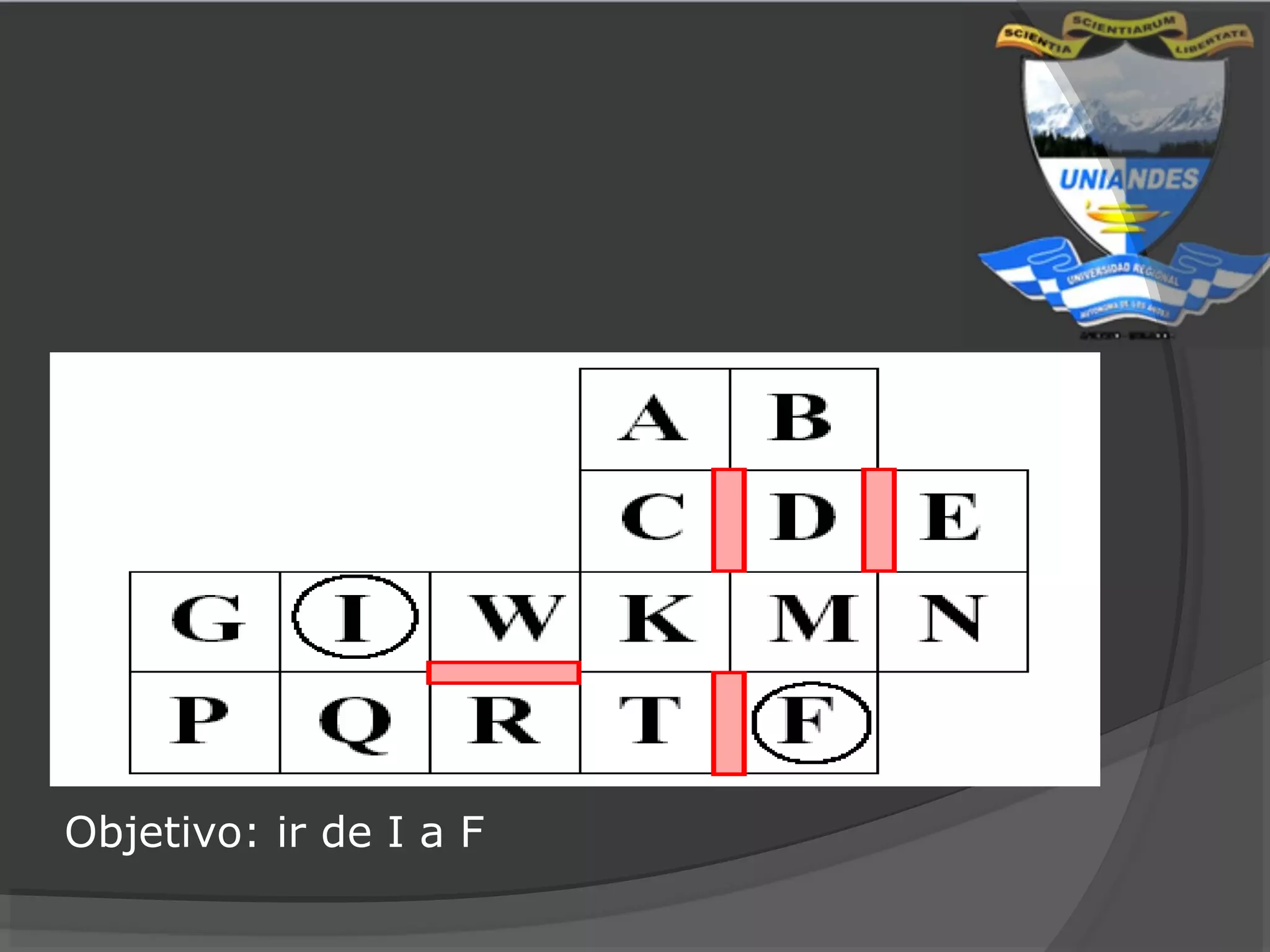
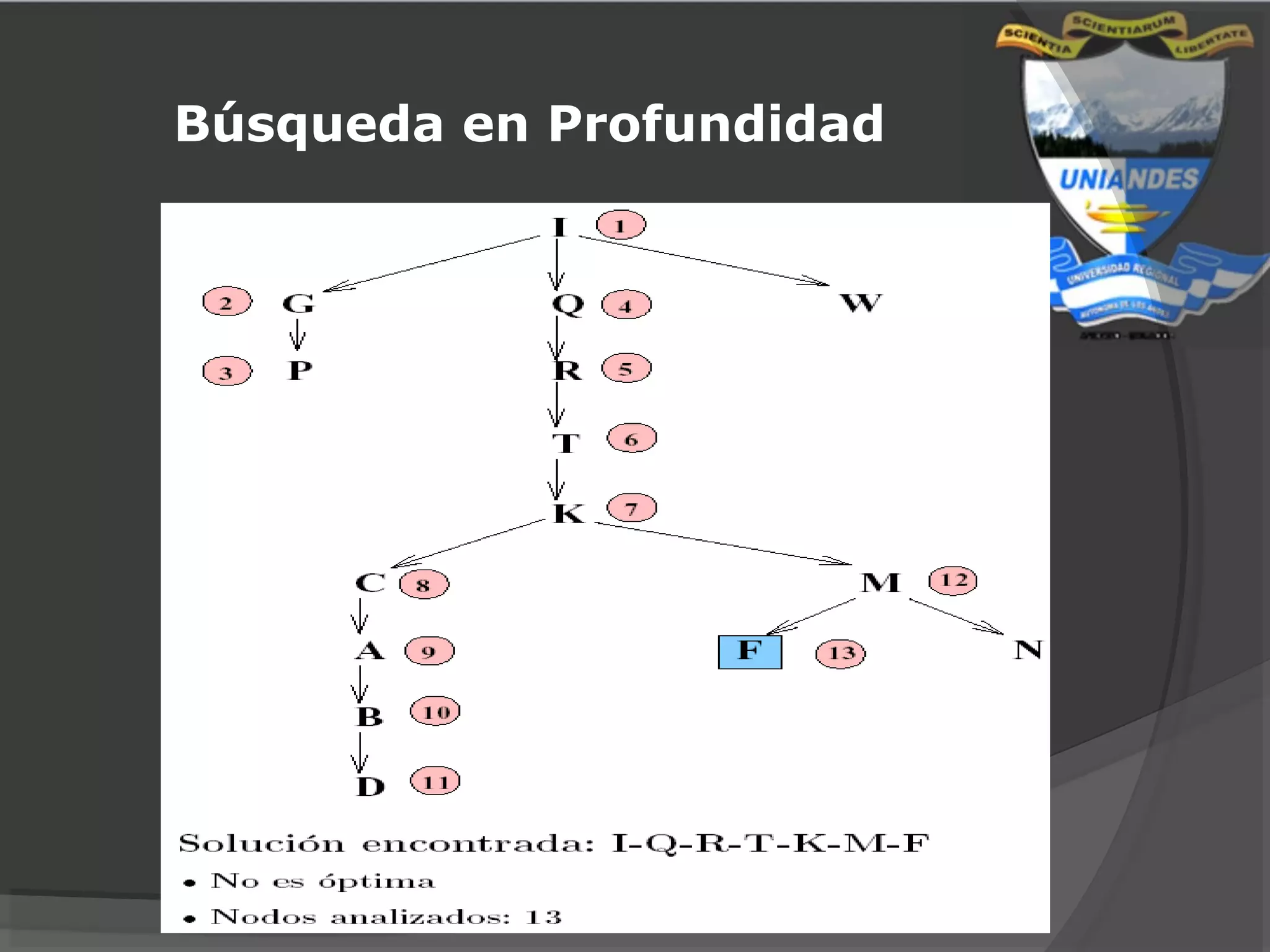
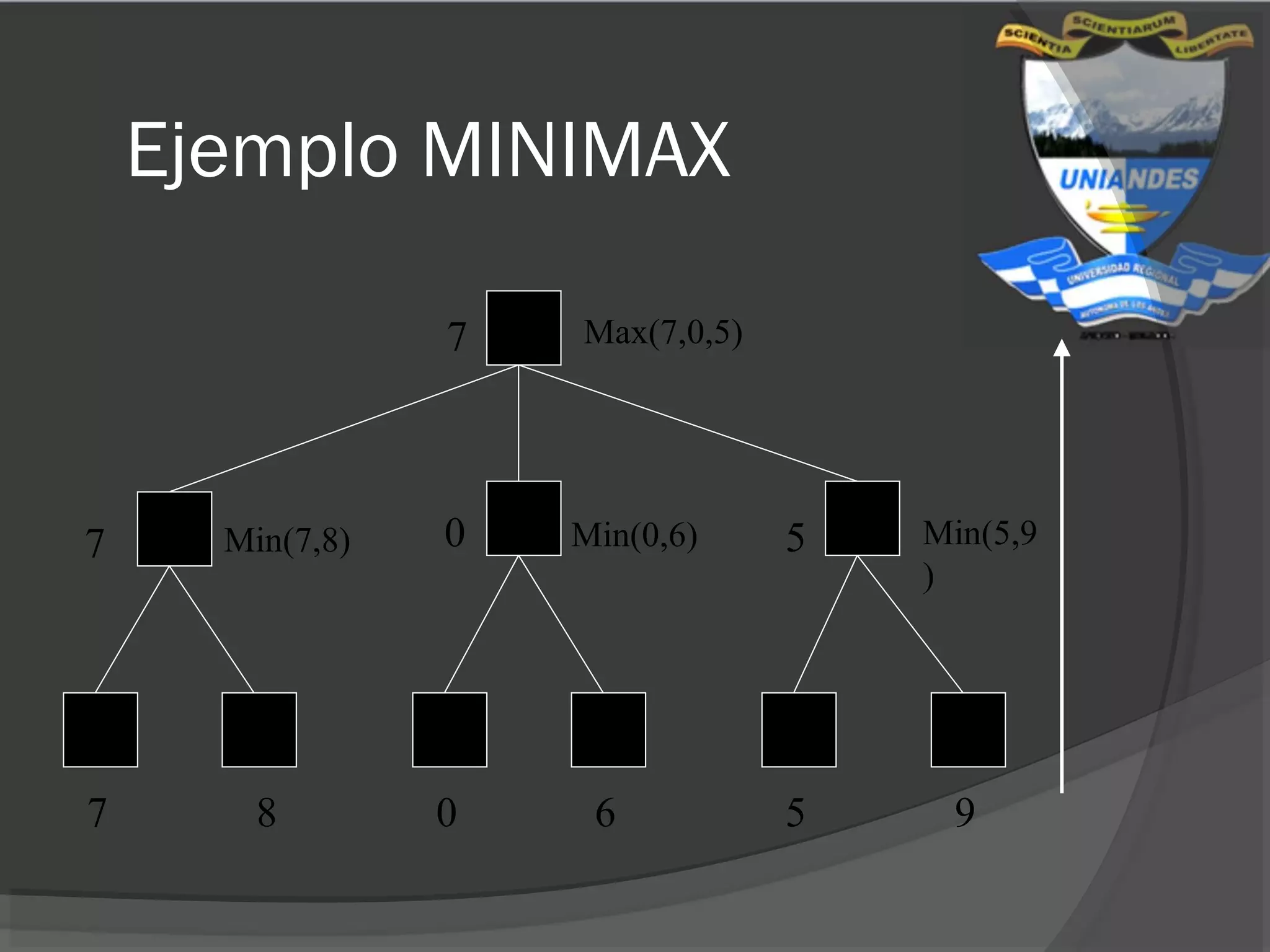
Este documento resume diferentes estrategias de búsqueda en inteligencia artificial, incluyendo búsquedas ciegas como profundidad y amplitud, búsquedas heurísticas que usan conocimiento del dominio, y búsquedas con adversarios como el algoritmo Minimax.

1. INTELIGENCIA ARTIFICIAL
BUSQUEDAS BASICAS
NOMBRE: Luis Cambal
CURSO: 6to Sistemas
FECHA: 22/07/2013

2. Estrategias de búsquedas
No Informadas ó a Ciegas: No se tiene
información adicional acerca de los estados. La
única información es la que proporciona la
formulación del problema.
Sólo generan sucesores y distinguen si han
llegado al objetivo ó no.
Informadas ó Heurísticas: Se conoce cuando
un estado no es objetivo, y si es mas
“prometedor” que otro.

3. S
A
B
C E
D
E
D F
Nodo Raíz
Nodo meta
El nodo raíz denota la trayectoria
que comienza y termina en el nodo
inicial S.
El hijo del nodo raíz con etiqueta A
Representa la trayectoria S-A.
Las trayectorias como S-A, que no
alcanzan las metas se conocen
como trayectorias Parciales. Las
trayectorias que alcanzan la meta
se llaman trayectorias completas, y
el nodo correspondiente es un
nodo meta.

4. METODOS CIEGOS
Búsqueda en Profundidad
Búsqueda en Amplitud
Búsqueda no Deterministica

5. Búsqueda en Profundidad
Toma los hijos de cada nodo y avanza a partir
de ese hijo.
Otras alternativas del mismo nivel se ignoran
por completo, en tanto haya posibilidades de
alcanzar la meta mediante la selección original.
Se busca en las ramas de izquierda a
derecha.

6. Búsqueda en Profundidad
1
17 18
5 6
2 8 13
3 7 9 12 14 16
4 10 11 15
goal

7. Revisa todas las trayectorias de una longitud
dada antes de avanzar a una trayectoria más
larga.
Búsqueda en Amplitud

8. Búsqueda en Amplitud
1
2 3 4
5 6 7 8 9 10
11 12 13 14
goal

9. Búsqueda no Determinística
Se puede tener tan poca información sobre un
problema al grado de que no sea posible
descartar un factor de ramificación grande o
trayectorias largas carentes de utilidad.
La búsqueda no determinística consiste en
buscar un termino medio entre la búsqueda en
profundidad y la búsqueda en amplitud.

10. Problema del Laberinto
En el siguiente laberinto, se puede pasar
desde una casilla a otra de las posibles
adyacentes (arriba, abajo, izquierda, derecha),
salvo si existe una barrera entre ellas

11. Objetivo: ir de I a F

12. Búsqueda en Profundidad

13. Búsqueda heurística
• Las técnicas de búsqueda heurística usan el
conocimiento del dominio para adaptar el solucionador
y, de esta manera, éste sea más potente y consiga llegar a la
solución con mayor rapidez. Por tanto, estas técnicas utilizan el
conocimiento para avanzar buscando la solución al problema.
• Definiciones:
- Costo del camino: coste necesario para ir del nodo raíz al
nodo meta por dicho camino.
- Costo para hallar la solución: coste necesario para encontrar
el camino anteriormente definido.
-Potencia heurística: capacidad de un método de exploración
para obtener la solución con un coste lo más bajo posible.

14. Función de evaluación
heurística
• Definición: es una aplicación del espacio de estados
con el espacio de los números reales
F(estado) => n
• n representa lo cercano que esta el estado con el que
se ha aplicado la función de evaluación de la solución
final.
• Es muy importante mantener un equilibrio entre la
eficiencia de la función y su complejidad. No debemos
tener una función de evaluación demasiado complicada,
ni tampoco una demasiado sencilla pero que no avance
prácticamente nada en el problema. En caso de no
mantener este equilibrio se podría producir explosión
combinatoria.

15. Estrategias de búsqueda
heurística
• Tipos:
• Estrategias tentativas: aquellas en las que se puede
abandonar la exploración de una rama y pasar a
explorar otra en cualquier momento del problema.
• Estrategias irrevocables: aquellas en las que no se
puede abandonar la exploración de la rama por la
que se comenzó.
•Métodos:
• Gradiente
• Primero el mejor
• Búsqueda en haz
• Algoritmo A

16. Estrategias de búsqueda
heurística
 Gradiente:
• Metodología: elegir el camino de máxima pendiente,
usando para ello la función de evaluación.
• Tipo: irrevocable.
• Ventajas: se llega a la solución con poco coste
computacional.
• Inconvenientes: puede ser que el problema no sea
compatible con este método, y, por lo tanto, no
conseguiremos obtener la solución.

17. Estrategias de búsqueda
heurística
 Primero el mejor:
• Metodología: elegir como siguiente nodo aquel con
mayor función de evaluación.
• Tipo: tentativo.
• Ventajas: no depende en exceso de la función de
evaluación.
• Inconvenientes: excesiva complejidad espacial,
pues se deben guardar todos los nodos abiertos.

18. Estrategias de búsqueda
heurística
 Búsqueda en haz:
• Metodología: elegir un conjunto de nodos como los
siguientes a expandir, y hacerlo de forma irrevocable.
• Tipo: irrevocable/tentativo.
• Ventajas: más permisible.
• Inconvenientes: en caso de que el sistema sea
irrevocable, este método no actúa con eficacia.

19. Búsqueda con adversos
La búsqueda con adversos (juego contra un oponente)
analiza los problemas en los que existe mas de un
adversario modificando el estado del sistema.
Hay dos operadores:
- el que lleva el problema a la mejor situación (jugada
nuestra)
- el que lleva el problema a la peor situación (jugada
de nuestro adversario)

20. Búsqueda con adversos:
Algoritmo MINIMAX
- Minimax es un método de decisión para minimizar la
pérdida máxima esperada en juegos con adversario y
con información perfecta.
- Minimax es un algoritmo recursivo.
- El funcionamiento de Minimax puede resumirse como
elegir mejor movimiento para ti mismo suponiendo que tu
contrincante escogerá el peor para ti.

21. Pasos del algoritmo
Minimax
1. Generación del árbol de juego. Se generarán todos
los nodos hasta llegar a un estado terminal.
2. Cálculo de los valores de la función de evaluación
para cada nodo terminal.
3. Calcular el valor de los nodos superiores a partir del
valor de los inferiores.
4. Desde los nodos de nivel n, buscar la mejor
situación para mi y la peor para mi rival. Elegir la
jugada valorando los valores que han llegado al
nivel superior, es decir, obtengo la mejor rama.

22. Búsqueda con adversos:
Algoritmo MINIMAX
El algoritmo explorará los nodos del árbol asignándoles
un valor numérico mediante una función de evaluación,
empezando por los nodos terminales y subiendo hacia
la raíz.
La función de evaluación definirá lo buena que es la
posición para un jugador cuando la alcanza. Ejemplo:
en el ajedrez los posibles valores son (+1,0,-1) que se
corresponden con ganar, empatar y perder
respectivamente. Esto será diferente para cada juego.

23. Ejemplo MINIMAX
A
B C D
E F G H I J
7 8 0 6 5 9
Min(7,8) Min(0,6) Min(5,9
)
7 0 5
Max(7,0,5)7