Este documento presenta la resolución numérica de varias ecuaciones diferenciales ordinarias (EDO) mediante el método de Runge-Kutta implementado en el software MATLAB. Se transforman EDO de segundo orden en sistemas de primer orden equivalentes y se resuelven usando el integrador ode45. Los resultados muestran las curvas de solución y su convergencia a estados de equilibrio.

1. Universidad Simón I. Patiño
Docente: Francisco Medrano Rocha
Cálculo Numérico
Corrección de la lista de ejercicios 7 (en MATLAB)
Ejercicio 3. En primer lugar se debe transformar esta EDO de segundo orden en un sistema de
primer orden. Por lo tanto deben introducirse nuevas variables, tantas como valores iniciales
tenga el problema. En este caso hay dos valores iniciales, uno sobre el desplazamiento angular
θ y otro sobre la velocidad angular θ . Nuestra ecuación original es
2
3
ml2
θ + 0,99θ +
1
2
mgl sin θ = 0 (1)
Introduciendo las variables u1(t) = θ(t) y u2(t) = θ (t) (que es equivalente a considerar la
función vectorial de variable t siguiente u = (u1(t), u2(t))T
). Derivando esas variables se tiene
u1 = θ = u2
u2 = θ =
2
3ml2
−0,99u2 −
1
2
mgl sin u1
esto teniendo en cuenta que u2 = θ se obtiene despejando de la ecuación (1) y u1 = θ.
Podemos escribir el sistema anterior como sigue:
u (t) =
u1(t)
u2(t)
=
u2(t)
3
2ml2 0,99u2(t) − 1
2
mgl sin u1(t)
f(t,u)
= f(t, u) (2)
Ahora la ecuación (2) es un sistema de primer orden y puedo aplicar un método numérico o
un resolvedor de MATLAB, en este caso usaremos ode45.
Trataremos el caso θ(0) = 15◦
= 15
360
2π (conversión en radianes), θ (0) = 0 (velocidad angular
0, la masa m es "soltada").
En primer lugar debemos escribir en MATLAB la función f que describa el miembro de la
derecha del sistema (2). Tomando en cuenta que según los datos del problema ml2
= 1,28 y
g/l = 7,45:
f=i n l i n e ( ’ [ u (2) ; −0.105469∗u (2) −5.5875∗ sin (u (1) ) ] ’ , ’ t ’ , ’u ’ )
Vamos entonces a resolver este sistema en el intervalo [0, 5], es decir t0 = 0 y TF = 5. El
valor inicial de el sistema (2) es u0 = (u1(0), u2(0)) = (θ(0), θ (0)) = ( 15
360
2π, 0). Podemos
llamar entonces a ode45 con la instrucción siguiente:
u0=[(15∗2∗ pi ) /360;0] % para e l valor i n i c i a l
[ t , u]=ode45 ( f , [ 0 , 5 ] , u0 ) % c a l c u l o de la solucion
Recuerde que la variable t contiene la discretización del tiempo y u es una matriz cuyas
columnas son u1(tn) y u2(tn) para cada tn de la discretización de t.
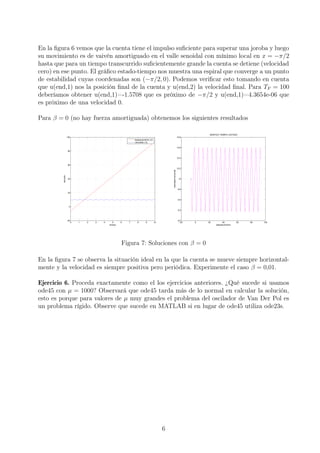
Para obtener el gráfico del tiempo versus θ(t) (tiempo vs desplazamiento angular) escribimos
la instrucción:
plot ( t , u ( : , 1 ) )
1

2. Para el gráfico del tiempo versus θ (t) (tiempo vs velocidad angular):
plot ( t , u ( : , 2 ) )
Si queremos el gráfico de tiempo-estado escribimos la instrucción:
plot (u ( : , 1 ) ,u ( : , 2 ) )
legend ( ’ angulo ’ , ’ velocidad ␣ angular ’ )
Para recuperar θ y θ al cabo de TF damos las instrucciones:
u(end , 1 ) % para e l angulo f i n a l
u(end , 2 ) % para la velocidad f i n a l
0 5 10 15 20 25 30
−0.8
−0.6
−0.4
−0.2
0
0.2
0.4
0.6
posición
velocidad
−0.4 −0.3 −0.2 −0.1 0 0.1 0.2 0.3
−0.8
−0.6
−0.4
−0.2
0
0.2
0.4
0.6
DIAGRAMA TIEMPO−ESTADO
Figura 1: Soluciones con TF = 30
Para un tiempo más grande, digamos TF = 30 vemos que tanto el angulo barrido como la
velocidad del péndulo experimentan un efecto amortiguado, es decir ambas curvas solución
se aproximan del valor 0 (el péndulo alcanza su posición de equilibrio y deja de moverse) una
situación que corresponde a la realidad. Al mismo tiempo el gráfico tiempo-estado representa
una espiral que parte de la condición inicial 15◦
(o lo mismo 30π
360
radianes) y velocidad angular
0 (simplemente se suelta la masa en ese ángulo), esta espiral converge al punto de equilibrio
(0, 0) que es la situación en la que, luego de haber transcurrido mucho tiempo, el péndulo
esta en equilibrio.
Ejercicio 4. Nuestra EDO original es de segundo orden:
x + 0,6x + x3
= 100e−t/3
(3)
debemos transformarla en un sistema de primer orden. Hay dos valores iniciales, uno sobre
x(0) = 0 y otro sobre x (0) = 1. Por lo tanto introduciremos 2 variables nuevas u1(t) = x(t)
y u2(t) = x (t). Derivando esas variables:
u1 = x = u2
u2 = x = −0,6x − x3
+ 100e−t/3
= 0,6u2 − u3
1 + 100e−t/3
Es decir tenemos el sistema
u (t) =
u1(t)
u2(t)
=
u2(t)
−0, 6u2(t) − u1(t)3
+ 100e−t/3 = f(t, u) (4)
2

3. Vamos a resolver este sistema en el intervalo [0, 5], esto es t0 = 0 y TF = 5. La condición
inicial del sistema es u0 = (u1(0), u2(0)) = (x(0), x (0)) = (0, 1).
Primeros escribimos la función f del miembro de la derecha de (4) en MATLAB:
f=i n l i n e ( ’ [ u (2) ; −0.6∗u (2)−u (1) ^3+100∗exp(−t /3) ] ’ , ’ t ’ , ’u ’ )
Luego utilizamos ode45:
u0 =[0;1] % la condicion i n i c i a l
[ t , u]=ode45 ( f , [ 0 , 5 ] , u0 ) ; % c a l c u l o de la solucion
plot ( t , u ( : , 1 ) ) % g r a f i c o del desplazamiento x ( t )
plot ( t , u ( : , 2 ) ) % g r a f i c o de la velocidad x ’ ( t )
plot (u ( : , 1 ) ,u ( : , 2 ) ) % g r a f i c o tiempo−estado
legend ( ’ posicion ’ , ’ velocidad ’ ) % l o s valores de cada eje coordenado
u(end , 1 ) % e l desplazamiento f i n a l ( al cabo de T_F)
u(end , 2 ) % la velocidad f i n a l ( al cabo de T_F)
Pruebe los mismos comandos esta vez utilizando ode23s:
[ t , u]=ode23s ( f , [ 0 , 5 ] , u0 ) ;
0 1 2 3 4 5 6 7 8 9 10
0
2
4
6
8
tiempo en segundos
desplazamientoenmetros
0 1 2 3 4 5 6 7 8 9 10
−40
−20
0
20
40
tiempo
velocidadenm/s
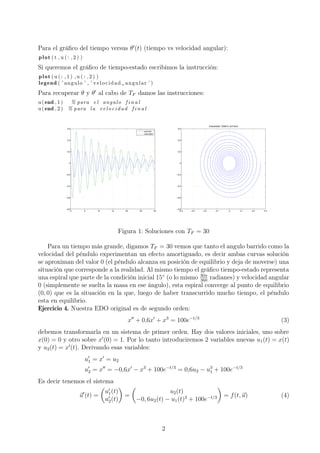
Figura 2: Soluciones hasta TF = 10
La figura 2 muestra las soluciones para x(t) y x (t). Debido a la presencia de una amor-
tiguamiento viscoso la masa experimenta un movimiento de vaivén amortiguado, con un
desplazamiento y velocidad que tienden a cero. En la figura 3, el gráfico tiempo-estado (des-
plazamiento vs velocidad) nos muestra que se parte de (0,1) y para una tiempo transcurrido
muy grande se alcanza el estado de equilibro (0,0) donde la masa ya no se mueve y regresa
a su posición inicial.
3

4. 0 1 2 3 4 5 6 7 8
−25
−20
−15
−10
−5
0
5
10
15
20
25
GRAFICO: desplazamiento vs velocidad
desplazamiento
velocidad
Figura 3: Gráfico estado-tiempo para TF = 100
Ejercicio 5.
Figura 4: Deslizamiento de una cuenta
Luego de hacer un diagrama de cuerpo libre, horizontalmente actúan sobre la cuenta la
componente en x, Dx = −β dx
dt
de la fuerza amortiguada D y la componente en x de la fuerza
tangencial debida al peso Fx = −mg sin θ cos θ. Tomando en cuenta que f (x) = tan θ y
1 + tan2
θ = sec2
θ, sin2
θ + cos2
θ = 1 obtenemos
Fx = −mg
f (x)
1 + f (x)2
Por la segunda ley de Newton mx = −Fx +Dx. Es decir, tenemos la EDO de segundo orden
siguiente:
mx = −mg
f (x)
1 + f (x)2
− βx (5)
Nuevamente hay dos valores iniciales en este problema, uno para la posición x(t) y otro para
la velocidad x (t), debemos por tanto introducir dos nuevas variables: u1 = x y u2 = x .
Derivando esas variables:
u1 = x = u2
u2 = x = −g
f (x)
1 + f (x)2
−
β
m
u2
4

5. Esto es equivalente al sistema de primer orden siguiente:
u (t) =
u1(t)
u2(t)
=
u2(t)
−g f (x)
1+f (x)2 − β
m
u2(t)
= f(t, u) (6)
Resolvemos este sistema con ode45 y los datos siguientes: x(0) = −2π ≈ −6,2832 (posición
horizontal inicial), x (0) = 10 (velocidad inicial en dirección positiva, es decir a la derecha).
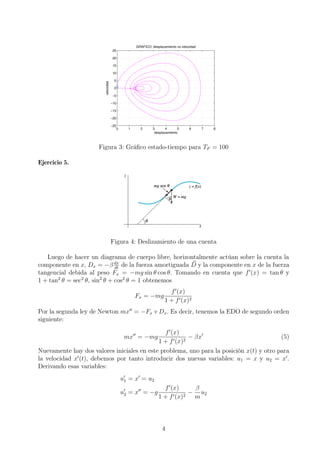
Como no se especifica el tiempo final TF , vamos a tomar TF = 100.
Figura 5: Deslizamiento de una cuenta en una onda senoidal
En la figura 5 la cuenta es impulsada en x(0) = −2π con una velocidad inicial x (0) = 10.
Escribimos la función f del sistema en MATLAB tomando en cuenta que m = 0, 1 kg,
g = 9, 8 m/s2
, β = 0,1 y que para f(x) = sin(x) tenemos f (x) = cos(x):
f=i n l i n e ( ’ [ u (2) ; −9.81∗ cos (u (1) ) /(1+ cos (u (1) ) ^2)−u (2) ] ’ , ’ t ’ , ’u ’ )
Luego con ode45:
u0=[−2∗pi ; 1 0 ] % la condicion i n i c i a l
[ t , u]=ode45 ( f , [ 0 , 1 0 0 ] , u0 ) ; % c a l c u l o de la solucion
plot ( t , u ( : , 1 ) ) % g r a f i c o del desplazamiento x ( t )
plot ( t , u ( : , 2 ) ) % g r a f i c o de la velocidad x ’ ( t )
plot (u ( : , 1 ) ,u ( : , 2 ) ) % g r a f i c o tiempo−estado
legend ( ’ posicion ’ , ’ velocidad ’ ) % l o s valores de cada eje coordenado
u(end , 1 ) % e l desplazamiento f i n a l ( al cabo de T_F)
u(end , 2 ) % la velocidad f i n a l ( al cabo de T_F)
0 1 2 3 4 5 6 7 8 9 10
−8
−6
−4
−2
0
2
4
6
8
10
tiempo
solución
desplazamiento x(t)
velocidad x‘(t)
−7 −6 −5 −4 −3 −2 −1 0 1
−4
−2
0
2
4
6
8
10
GRAFICO TIEMPO−ESTADO
desplazamiento
velocidadhorizontal
Figura 6: Soluciones con β = 0,1
5

6. En la figura 6 vemos que la cuenta tiene el impulso suficiente para superar una joroba y luego
su movimiento es de vaivén amortiguado en el valle senoidal con mínimo local en x = −π/2
hasta que para un tiempo transcurrido suficientemente grande la cuenta se detiene (velocidad
cero) en ese punto. El gráfico estado-tiempo nos muestra una espiral que converge a un punto
de estabilidad cuyas coordenadas son (−π/2, 0). Podemos verificar esto tomando en cuenta
que u(end,1) nos la posición final de la cuenta y u(end,2) la velocidad final. Para TF = 100
deberíamos obtener u(end,1)=-1.5708 que es próximo de −π/2 y u(end,1)=4.3654e-06 que
es próximo de una velocidad 0.
Para β = 0 (no hay fuerza amortiguada) obtenemos los siguientes resultados
0 1 2 3 4 5 6 7 8 9 10
−20
0
20
40
60
80
100
tiempo
solución
desplazamiento x(t)
velocidad x‘(t)
−20 0 20 40 60 80 100
9.2
9.4
9.6
9.8
10
10.2
10.4
10.6
10.8
GRAFICO TIEMPO−ESTADO
desplazamiento
velocidadhorizontal
Figura 7: Soluciones con β = 0
En la figura 7 se observa la situación ideal en la que la cuenta se mueve siempre horizontal-
mente y la velocidad es siempre positiva pero periódica. Experimente el caso β = 0,01.
Ejercicio 6. Proceda exactamente como el los ejercicios anteriores. ¿Qué sucede si usamos
ode45 con µ = 1000? Observará que ode45 tarda más de lo normal en calcular la solución,
esto es porque para valores de µ muy grandes el problema del oscilador de Van Der Pol es
un problema rígido. Observe que sucede en MATLAB si en lugar de ode45 utiliza ode23s.
6