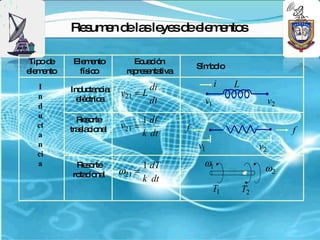
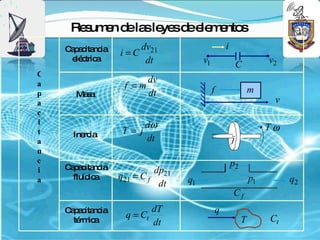
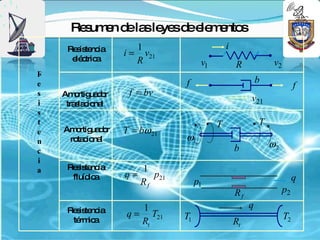
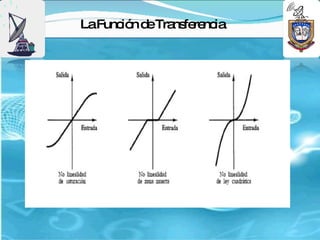
1) La función de transferencia describe el comportamiento de entrada-salida de un sistema mediante la relación entre las transformadas de Laplace de la salida y la entrada, suponiendo condiciones iniciales nulas. 2) Se presentan ejemplos de funciones de transferencia para circuitos RL, sistemas masa-amortiguador-resorte y diferentes elementos. 3) Existen diferentes clasificaciones de funciones de transferencia como respuesta al impulso, características espectrales y de fase.

1. REPUBLICA BOLIVARIANA DE VENEZUELA
MINISTERIO DEL PODER POPULAR PARA LA DEFENSA
UNIVERSIDAD NACIONAL EXPERIMENTAL POLITECNICA
DE LA FUERZA ARMADA
U.N.E.F.A
NUCLEO-CARABOBO EXTESION-GUACARA
Brs
Anthony Padilla 18. .241.596
Elio Peña 18.434.399
Jean C. Castillo 16.217.734
Pedro Calvo 11.356.115
Ing. Telecom
G-005-N

2. LaFunc n d Tra fe nc
ió e ns re ia
L [ c(t )] c(t ) = salida
Función de transferencia =
L [ r (t )] r (t ) = entrada
con condiciones iniciales cero
La Función de Transferencia:
La función de transferencia de un sistema se define como la transformada
de Laplace de la variable de salida y la transformada de Laplace de la variable de
entrada, suponiendo condiciones iníciales cero.
•Solo es aplicable a sistemas descritos por ecuaciones diferenciales lineales
invariantes en el tiempo.
•Es una descripción entrada salida del comportamiento del sistema.
•Depende de las características del sistema y no de la magnitud y tipo de entrada
•No proporciona información acerca de la estructura interna del sistema

3. LaFunc n d Tra fe nc
ió e ns re ia
La función de transferencia F[z] correspondiente a un sistema lineal e
invariante es la relación constante que existe entre las transformada Z de la salida y
de la entrada, para condiciones iníciales nulas.
Sistema lineal: Es aplicable el principio de superposición, de manera que la suma de
entradas produce la suma de salidas, y una entrada multiplicada por una constante
produce la misma salid multiplicada por la misma constante .
Sistema invariante en el Tiempo: Una entrada desplazada en el tiempo produce la
misma salida desplazada en el tiempo. En un sistema lineal, pero variable en el tiempo
los coeficientes dependes del tiempo K.
Algoritmo Lineal, en forma de ecuación diferencia
Usando la transformación Z, y específicamente sus propiedades de linealidad y
retardo, para señales casuales (condiciones iníciales nulas):

4. LaFunc n d Tra fe nc
ió e ns re ia
Sistema Casual: Es ejecutable en tiempo real, por lo que y[K] no depende de valores
futuro de la entrada µ[k+1].µ[k+2]…. Se admite el valor presente de la entrada µ[k],
suponiendo que el tiempo de calculo sea despreciable. Por tanto la función de
transferencia será una fracción propia (orden del numerador menor o igual que el del
denominador).
Sistema No Lineal: Un sistema es a-lineal, si no le puede aplicar el principio de
superposición. por tanto, para un sistema a-lineal la respuesta a dos entradas no
puede calcularse tratando cada una a la vez y sumando los resultados.
Los procedimientos para encontrar soluciones a problemas que involucran
sistemas a-lineales son complicados. Por ese motivo resulta necesario considera
sistema lineales “equivalente”. Tale sistema lineales ”equivalentes” son válidos sòlo
para un rango limitado de trabajo.

5. C ns e c ne
o id ra io s
• La funciones de transferencia de un sistema, es un modelo matemático; es un método
para expresar la ecuación diferencial que relaciona la variable de salida con la variables
de entrada.
• Es una propiedad de un sistema, independiente de su magnitud y naturaleza de la
función de entrada.
• Incluye las unidades necesarias para relacionar la entrada con la salida; pero no
proporciona información de la estructura física del sistema. (las funciones de
transferencia de muchos sistemas físicamente diferentes, pueden ser idénticas).
• Si se conoce la función de transferencia de un sistema se estudia la salida o respuesta
para varias forma de entrada, con la intención de comprender la naturaleza del sistema.
• Si se desconoce la función de transferencia de un sistema, puede establecerse
experimentalmente, introduciendo entradas conocidas y estudiando la salida del sistema.
• Una vez obtenida la función de transferencia, tendremos una descripción completa de las
características dinámicas del sistema, a diferencia de su descripción física.

6. LaFunc n d Tra fe nc
ió e ns re ia

7. Ejemplos de Funciones de Transferencia
R
1.- Circuito RL i (t )
Utiliza ole d vo je d Kirc ff, s tie :
nd y e lta s e hho e ne
v (t ) L
di
v(t ) = Ri (t ) + L
dt
Fig 1. C uitoRL
ura irc
Ap a o latra fo a ad La la ec n c nd io sinic le c ro
lic nd ns rm d e p c o o ic ne ia s e :
V ( s ) = RI ( s ) + LsI ( s )
lare c n c rrie vo jee La la e q d :
la ió o nte lta n p c , ue a
1
I (s) R
=
V ( s) L s + 1
R

8. Ejemplos de Funciones de Transferencia
2.- Sistema masa amortiguador resorte
Utiliza o la le sd Ne to s o tie :
nd s ye e w n, e b ne
d2y dy k
m 2 + b + ky (t ) = r (t )
dt dt
d nd m e lam s , b
o e s aa e e c e ie d fric ió vis o a
s l o fic nte e c n c s , b
k e lac ns nted l re o ,
s o ta e s rte y (t ) e e de pla m ntoy r (t )
s l s za ie
e lafue a lic d . Su tra fo a ad La la ee :
s rza p a a ns rm d e p c s
m
( ) ( )
M s 2Y ( s ) − sy (0 + ) − y ' (0 + ) + b sY ( s ) − y (0 + ) + KY ( s ) = R( s ) y(t)
y ' (0+ ) = 0, y (0+ ) = 0, r(t)
c ns e nd :
o id ra o
Fig 1. Sis m m s
ura te a a a
Am rtig d r re o .
o ua o s rte
Ms 2Y ( s ) + bsY ( s ) + KY ( s ) = R ( s )
Y ( s) 1
Lafunc n d tra fe nc e :
ió e ns re ia s =
R ( s ) Ms 2 + bs + K

9. Ejemplos de Funciones de Transferencia
2b.- Sistema masa amortiguador resorte con desplazamiento inicial
C ns é s a raq e teun d s la m nto inic l
o id re e ho ue xis e p za ie ia y0 . Entonce pa
s ra
c ns rva lac nd ió unae d unas lid s ha e
o e r o ic n ntra a a ae c r (t ) = 0
( ) ( )
M s 2Y ( s ) − sy (0 + ) − y ' (0 + ) + b sY ( s ) − y (0 + ) + KY ( s ) = R( s )
c nd io sinic le
o ic ne ia s r (t ) = 0, y ' (0+ ) = 0, y (0+ ) = y0 ,
Lafunc n d tra fe nc e :
ió e ns re ia s
Aho e d s la m nto s lo
ra l e p za ie o
y0 ( Ms + b) d p nd d lap s ió inic l
e e e e o ic n ia
Y (s) = y lo p rá e sd l s te a
s a m tro e is m .
Ms 2 + bs + K

10. Re um n d la le sd e m nto
s e e s ye e le e s
Tip d
o e Ele e
m nto Ec c n
ua ió
Sím o
b lo
e m nto
le e fís o
ic re re e tiva
p s nta
I di i L
Ind ta ia
uc nc v21 = L
n e c a
lé tric dt v1 v2
d
u
Re o
s rte 1 df
ct
tra la io l
s c na v21 = f f
a k dt
n v1 v2
ci
a Re o
s rte 1 dT ω1
ω21 = ω2
ro c na
ta io l
k dt
T1 T2

11. Re um n d la le sd e m nto
s e e s ye e le e s
C p c nc
a a ita ia dv i
i = C 21
e c a
lé tric dt v1 v2
C
C
dv
a f =m f m
p Ma a
s dt
a v
c
i dω
t T= j Tω
Ine ia
rc
a dt j
n
c p2
i C p c nc
a a ita ia dp21
a fluíd a
ic q21 = C f q1 p1 q2
dt
Cf
C p c nc
a a ita ia dT q
té ic
rm a
q = Ct T Ct
dt

12. Re um n d la le sd e m nto
s e e s ye e le e s
Re is nc
s te ia 1 i
i = v21
e c a
lé tric R v1 R v2
R
e f b
f
s Am rtig d r
o ua o f = bv
i
v21
tra la io l
s c na
s
t T T
e Am rtig d r
o ua o T = bω 21
n ro c na
ta io l ω1
b ω2
c
i
a Re is nc
s te ia 1
fluíd a
ic q= p21 q
Rf p1
Rf p2
1 q
Re is nc
s te ia q = T21
té ic
rm a T1 T2
Rt Rt

13. Tip sd func ne d tra fe nc
o e io s e ns re ia
La clasificación en el dominio del tiempo de una función de
transferencia de una secuencia LTI esta basada en la longitud
de su respuesta al impulso:
•Función de transferencia de Respuesta Finita al Impulso (FIR).
•Función de transferencia de Respuesta Infinita al Impulso (IIR).
Muchas otras clasificaciones son usadas:
•Para funciones de transferencia digital con respuestas de frecuencia
selectivas a la frecuencia, una clasificación esta basada en la forma de
la grafica de la función de magnitud |H(ω)| o la forma de la función de
fase θ(ω).
Basada en el espectro de magnitud, 4 tipos de filtros ideales
son usualmente definidos:
•Pasa Bajas, Pasa Altas, Pasa Banda, Rechazo de Banda.

14. Tip sd func ne d tra fe nc
o e io s e ns re ia
Hasta ahora hemos visto funciones de transferencia caracterizadas
inicialmente de acuerdo a su:
• Longitud de respuesta al impulso (FIR/IIR).
•Características de los espectros de magnitud.
Una tercera clasificación de las funciones de transferencia es con
respecto a sus características de fase.
•Fase cero.
•Fase lineal.
•Fase lineal generalizados.
•Fase no lineal.
En muchas aplicaciones, es necesario que el filtro digital diseñado
no distorsione la fase de los componentes de la señal de entrada con
frecuencias en la banda de paso.