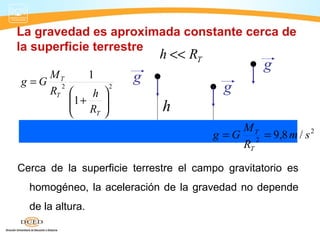
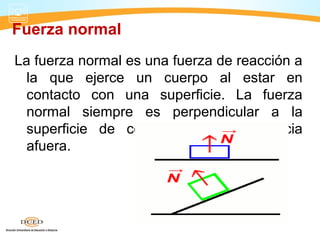
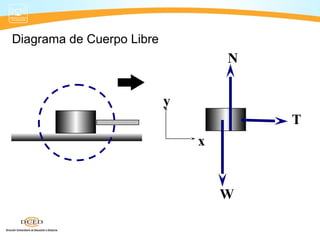
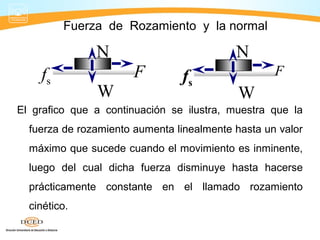
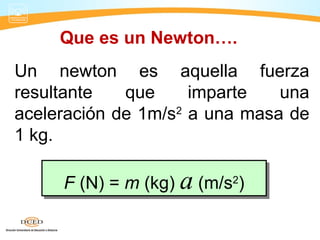
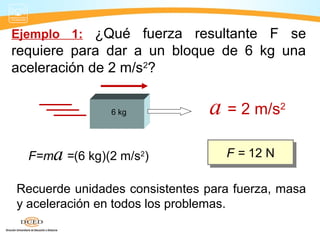
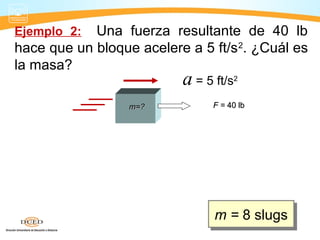
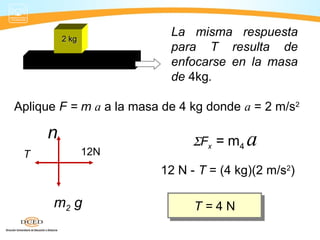
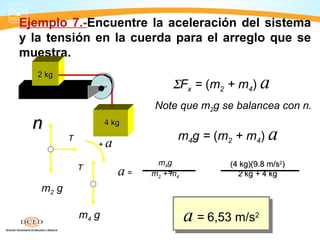
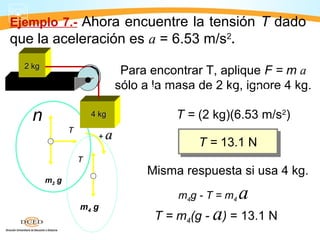
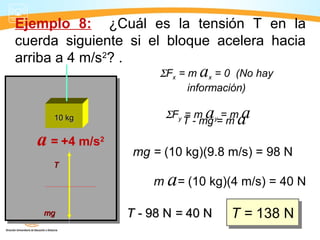
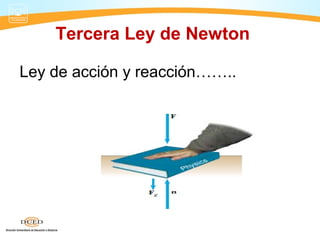
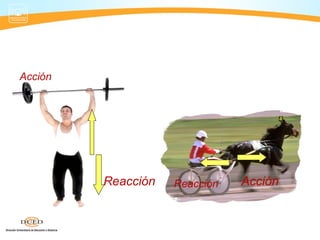
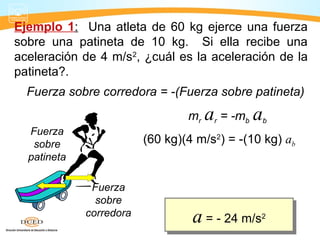
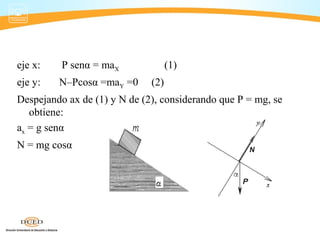
Este documento presenta información sobre dinámica, incluyendo fuerzas de fricción, las leyes de Newton y la gravitación universal. Cubre temas como sistemas de referencia inerciales, interacción de cuerpos, fuerza normal, diagrama de cuerpo libre, rozamiento estático y cinético, y aplicaciones de las leyes de Newton como problemas de una y dos masas.

1. DINAMICA

2. • Dinámica
• Fuerza de Fricción
• Leyes de Newton
• Gravitación Universal
CONTENIDOS TEMÁTICOS

3. DINAMICA
Es una parte de la mecánica que estudia la
reacción existente entre las fuerzas y los
movimientos que producen.

4. Sistema de Referencia Inercial.-
Es aquel sistema que carece de todo tipo de
aceleración.

5. Interacción de los Cuerpos
Todo cuerpo genera alrededor de el un campo
físico (gravitatorio, eléctrico, magnético, etc.);
ahora, si un cuerpo esta inmerso en el campo de
otro, se dice que dichos cuerpos están
interactuando entre si.

6. Fuerza de Fricción
Aparecen cuando hay fricción del cuerpo o
sistema con el medio que lo rodea y como
consecuencia de ello se produce que el sistema
pierda energía. Se define como el producto de la
normal y un coeficiente de fricción.

7. Fuerza normal
La fuerza normal es una fuerza de reacción a
la que ejerce un cuerpo al estar en
contacto con una superficie. La fuerza
normal siempre es perpendicular a la
superficie de contacto y dirigida hacia
afuera.

8. Diagrama de Cuerpo Libre
N
W
T
y
x

9. N
W
fs
F
N
W
fs
F
Fuerza de Rozamiento y la normal
El grafico que a continuación se ilustra, muestra que la
fuerza de rozamiento aumenta linealmente hasta un valor
máximo que sucede cuando el movimiento es inminente,
luego del cual dicha fuerza disminuye hasta hacerse
prácticamente constante en el llamado rozamiento
cinético.

11. Algunas Ventajas del Rozamiento
-Gracias al rozamiento podemos caminar, impulsando uno
de nuestros pies (el que esta en contacto con el suelo)
hacia atrás.
-Gracias al rozamiento las ruedas pueden rodar.
-Gracias al rozamiento podemos efectuar movimientos
curvilíneos sobre la superficie.
-Gracias al rozamiento podemos incrustar clavos en las
paredes.
Algunas Desventajas del Rozamiento
-Debido al rozamiento los cuerpos en roce se desgastan,
motivo por el cual se utilizan los lubricantes.
-Para vencer la fuerza de rozamiento hay que realizar
trabajo, el cual se transforma en calor.

12. Primera Ley de Newton
En ausencia de fuerzas externas
un objeto en reposo permanecerá
en reposo y un objeto en
movimiento continuará en
movimiento a velocidad
constante( esto es, con rapidez
constante en una línea recta).Tiende a seguir en movimiento…..
LEYES DE NEWTON

13. Segunda ley de Newton
Siempre que una fuerza resultante
actúa sobre un objeto, produce una
aceleración: una aceleración que es
directamente proporcional a la fuerza
e inversamente proporcional a la
masa.
Siempre que una fuerza resultante
actúa sobre un objeto, produce una
aceleración: una aceleración que es
directamente proporcional a la fuerza
e inversamente proporcional a la
masa.
F
a
m
∝

14. ∆∆FF
∆∆aa = Constante= Constante
Inercia o masa de 1 slug = 1 lb/(ft/s2
)
Masa m = 2 slugs
Gráfica Fuerza y Aceleración
FF
aa
∆F
∆a
∆F
∆a == Constante

15. Aceleración y fuerza
Empujar el carro con el doble de fuerza produce el
doble de aceleración. Tres veces la fuerza triplica la
aceleración.

16. Aceleración y Fuerza
4 lb
F
a = 2 ft/s2
La aceleración a es directamente proporcional a la
fuerza F y está en la dirección de la fuerza. En este
experimento se ignoran las fuerzas de fricción.
8 lb a = 4 ft/s2
F
12 lb a = 6 ft/s2
F

17. Un newton es aquella fuerza
resultante que imparte una
aceleración de 1m/s2
a una masa de
1 kg.
F (N) = m (kg) a (m/s2
)F (N) = m (kg) a (m/s2
)
Que es un Newton….

18. Equivalencias
1 N = 0,225 lb
1 lb = 4,45 N

19. Medida de la intensidad de una Fuerza

20. Ejemplo 1: ¿Qué fuerza resultante F se
requiere para dar a un bloque de 6 kg una
aceleración de 2 m/s2
?
6 kg a = 2 m/s2
F=ma =(6 kg)(2 m/s2
) F = 12 NF = 12 N
Recuerde unidades consistentes para fuerza, masa
y aceleración en todos los problemas.

21. Ejemplo 2: Una fuerza resultante de 40 lb
hace que un bloque acelere a 5 ft/s2
. ¿Cuál es
la masa?
F =F = 40 lb40 lbm=?m=?
a = 5 ft/s2
m = 8 slugsm = 8 slugs
or
F
F ma m
a
= =
2
40 lb
5 ft/s
F
m
a
= =

22. Ejemplo 3. Una fuerza neta de 4.2 x 104
N actúa sobre
un avión de 3.2 x 104
kg durante el despegue. ¿Cuál
es la fuerza sobre el piloto del avión, de 75 kg?
F = 4.2 x 104
N
m = 3.2 x 104
kg
++
F = ma
4
4
4.2 x 10 N
3.2 x 10 kg
F
a
m
= = a = 1.31 m/s2
F = ma = (75 kg)(1.31 m/s2
); F = 98.4 N
Primero encuentre
la aceleración a del
avión.

23. Ejemplo 4. Una pelota de tenis de 54 gm está
en contacto con la raqueta durante una
distancia de 40 cm cuando sale con una
velocidad de 48 m/s. ¿Cuál es la fuerza
promedio sobre la pelota?.
Dadas: vo = 0; vf = 48 m/s x = 0.40 m; m
= 0.0540 km; a = ¿?
Dadas: vo = 0; vf = 48 m/s
x = 40 cm; m = 54 gm
a = ¿?

24. Ejemplo 4 (Cont). Una pelota de tenis de 54 gm está
en contacto con la raqueta durante una distancia de
40 cm cuando sale con una velocidad de 48 m/s.
¿Cuál es la fuerza promedio sobre la pelota?.
2 2
02 ;fax v v= −
00
2
2(48 m/s)
; 2880 m/s
2(0.40 m)
a a= =
F= (0.054 kg)(2880 m/s2
); F = 156 N
F = maF = ma
2
2
fv
a
x
=

25. Ejemplo 5: Una calesa y su conductor tienen
una masa de 120 kg. ¿Qué fuerza F se
requiere para dar una aceleración de 6 m/s2
sin
fricción?.
Diagrama para calesa:
n
W
F

26. Ejemplo . ¿Qué fuerza F se requiere
para dar una aceleración de 6 m/s2
?
ΣFy = 0; n - W = 0
La fuerza normal, n,
es igual al peso ,W.
ΣFx = max; F = ma
F = (120 kg)(6 m/s2
)
F = 720 N
Diagrama para calesa:
n
W
F
x
+
m =m = 120 kg120 kg

27. Ejemplo 6.- Problema de dos cuerpos: Encuentre
la tensión en la cuerda de conexión si no hay
fricción sobre las superficies.
2 kg 4 kg
12 N
Primero aplique, F = ma, a todo el sistema
12 N
nn
(m2 + m4)g
ΣFx = (m2 + m4) a
12 N = (6 kg) a
a =
12 N
6 kg a = 2 m/s2a = 2 m/s2

28. 2 kg 4 kg
12 N
Aplique F = m a a la masa de 2 kg donde a = 2 m/s2
.
T
n
m2 g
ΣFx = m2 a
T = (2 kg)(2 m/s2
)
T = 4 NT = 4 N

29. 2 kg2 kg
La misma respuesta
para T resulta de
enfocarse en la masa
de 4kg.
Aplique F = m a a la masa de 4 kg donde a = 2 m/s2
ΣFx = m4 a
12 N - T = (4 kg)(2 m/s2
)
T = 4 NT = 4 N
12N
n
m2 g
T

30. Ejemplo 7.-Encuentre la aceleración del sistema
y la tensión en la cuerda para el arreglo que se
muestra.
ΣFx = (m2 + m4) a
a = 6,53 m/s2a = 6,53 m/s2
nn
m2 g
TT
m4 g
TT
+ a
Note que m2g se balancea con n.
m4g = (m2 + m4) a
(4 kg)(9.8 m/s(4 kg)(9.8 m/s22
))
22 kgkg ++ 4 kg4 kga = =
m4g
m2 + m4
22 kgkg
44 kgkg

31. Ejemplo 7.- Ahora encuentre la tensión T dado
que la aceleración es a = 6.53 m/s2
.
Para encontrar T, aplique F = m a
sólo a la masa de 2 kg, ignore 4 kg.
T = (2 kg)(6.53 m/s2
)
T = 13.1 NT = 13.1 N
Misma respuesta si usa 4 kg.
m4g - T = m4 a
T = m4(g - a) = 13.1 N
n
m2 g
TT
m4 g
TT
++ aa
22 kgkg
4 kg4 kg
ΣFx = m2a o T = m2a

32. Ejemplo 8: ¿Cuál es la tensión T en la
cuerda siguiente si el bloque acelera hacia
arriba a 4 m/s2
? .
1010 kgkg
a = +4 m/s2
TT
mgmg
ΣFx = m ax = 0 (No hay
información)
ΣFy = m ay = m aT - mg = m a
mg = (10 kg)(9.8 m/s) = 98 N
m a= (10 kg)(4 m/s) = 40 N
T -T - 98 N98 N == 40 N40 N T = 138 NT = 138 N

33. Tercera Ley de Newton
Ley de acción y reacción……..

34. Acción
Reacción AcciónReacción

35. Mas ejemplos de tercera ley….

36. Ejemplo 1: Una atleta de 60 kg ejerce una fuerza
sobre una patineta de 10 kg. Si ella recibe una
aceleración de 4 m/s2
, ¿cuál es la aceleración de la
patineta?.
Fuerza sobre corredora = -(Fuerza sobre patineta)
mr ar = -mb ab
(60 kg)(4 m/s2
) = -(10 kg) ab
a = - 24 m/s2a = - 24 m/s2
Fuerza
sobre
corredora
Fuerza
sobre
patineta
2(60 kg)(4 m/s)
24 m/s
-(10 kg)
a = = −

37. Ejemplos de Aplicación
1.Si un bloque de masa m se ubica sobre un plano sin roce,
inclinado un ángulo α con la horizontal, como se muestra en la
figura, partiendo del reposo, resbalará una distancia D a lo
largo del plano. Describir su movimiento.
Solución
Σ Fr = ma Σ F⇒ X = maX, Σ FY = maY = 0
Las fuerzas aplicadas sobre el cuerpo de masa m son la fuerza de
atracción de la Tierra, que es su peso P y la fuerza normal N
del plano sobre el cuerpo. Del diagrama de cuerpo libre
(figura), considerando que el bloque resbala en dirección del
plano, o sea en dirección x, tiene sólo ax y no ay

38. eje x: P senα = maX (1)
eje y: N–Pcosα =maY =0 (2)
Despejando ax de (1) y N de (2), considerando que P = mg, se
obtiene:
ax = g senα
N = mg cosα

39. 2.En el sistema mecánico de la figura, el bloque de masa M se
ubica sobre el plano liso inclinado en un ángulo α. La polea
por donde cuelga otro bloque de masa m conectado a M es
ideal y la cuerda se considera inextensible y de masa
despreciable. Calcular la aceleración de las masas M y m y la
tensión de la cuerda.
Solución:
Σ Fr = ma Σ F⇒ X = maX, Σ FY = maY = 0
Como no se conoce la dirección del movimiento, podemos
suponer que el cuerpo de masa M sube por el plano inclinado,
lo que determina el sentido de la aceleración del sistema,
entonces del DCL para M (figura 1)

40. De (3) se despeja T y se reemplaza en (1) y para
m ,figura 2, se obtiene:
eje x: T - Mg senα = Ma (1)
eje y: T - mg = -ma (3)
eje y: N - Mg cosα = 0 (2)

42. 3. En el sistema mecánico de la figura, se aplica una fuerza F
inclinada un ángulo α sobre el cuerpo de masa m, ubicado sobre
la mesa horizontal con coeficiente de roce μ. La polea por donde
cuelga otro bloque de masa M no tiene roce y la cuerda se
considera inextensible y de masa despreciable. Calcular la
aceleración de las masas y la tensión de la cuerda.
Solución: El sistema está en movimiento, por lo que se
aplica la segunda Ley de Newton a cada masa:
Σ Fr = ma Σ F⇒ X = maX, Σ FY = maY = 0
Para m Para M
eje x: T - Fcosα - FR = ma (1) eje y: T - Mg
= -Ma (3)
eje y: N + Fsenα - mg= 0 (2)

43. Además se sabe que por definición, la fuerza de roce es: FR =μ N.
De (2) se despeja N y se reemplaza en FR:
N = mg - Fsenα ⇒ FR =μ(mg - Fsenα) (4)
De (3) se despeja T: T = Mg - Ma (5)
Ahora (4) y (5) se reemplazan en (1), lo que permite despejar la
aceleración

45. 4.La persona de la imagen tiene una masa de 70Kg y sube
al ascensor equipado con una báscula en el piso.
¿Cuánto marcará la báscula si el ascensor
asciende con velocidad constante?
¿Asciende con aceleración de 2m/s2
?
¿Desciende con aceleración de 2m/s2
?

46. 5.Para la figura, la fuerza normal sobre el bloque amarillo
es
a) 2 N b) 20 N c) 10 N d) 100 N e) 200 N

47. 6.Para la figura, la aceleración del bloque amarillo es
a) 0 m/s2
b) 2m/s2
c) 8 m/s2
d) 10 m/s2
e) 20 m/s2
[ ]kg2
[ ]kg8

48. 7.Para la figura, la tensión en la cuerda es
a) 2N b) 8N c) 10N d) 16N e) 20N
[ ]kg2
[ ]kg8

49. LEY DE LA GRAVITACION UNIVERSAL DE
NEWTON

50. Esta ley establece que la fuerza de atracción gravitatoria
entre dos cuerpos cualesquiera del Universo es
directamente proporcional al producto de las masas de los
dos cuerpos que se atraen e inversamente proporcional al
cuadrado de la distancia que media entre ellos. Escrita
analíticamente la ley tiene por expresión:

51. Donde m1 y m2 son las masas de los dos cuerpos, r
la distancia que los separa y G es la constante de
la gravitación. Cuando se habla de la distancia
entre los dos cuerpos hay que entenderlo como la
distancia entre sus centros.
G=6,67 X 10-11
Nm2
/Kg2

52. Ejemplo
Dos esferas de plomo de 8Kg se colocan de modo que sus
centros están separados 0,5m.¿cuál es la magnitud de la
fuerza gravitacional que cada una ejerce sobre la otra?.
Solución

53. FUERZA GRAVITATORIA (HOMOGENEA)FUERZA GRAVITATORIA (HOMOGENEA)
h
g 2
r
M
Gg T
=
hRr T +=
( )
22
2
1
1






+
=
+
=
T
T
T
T
T
R
hR
M
Gg
hR
M
Gg

54. La gravedad es aproximada constante cerca de
la superficie terrestre
TRh <<
h
g22
1
1






+
=
T
T
T
R
hR
M
Gg
g
g
2
2
/8,9 sm
R
M
Gg
T
T
==
Cerca de la superficie terrestre el campo gravitatorio es
homogéneo, la aceleración de la gravedad no depende
de la altura.

55. GRACIAS