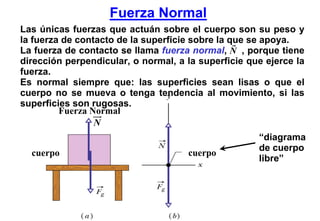
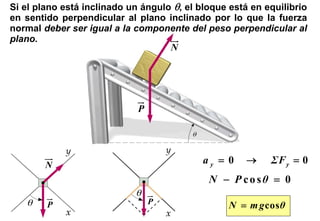
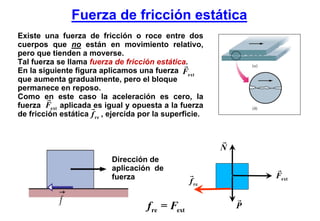
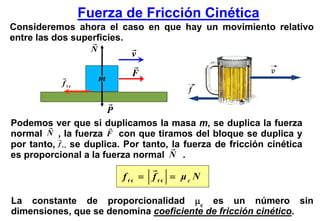
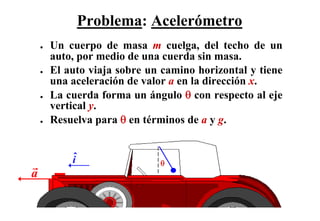
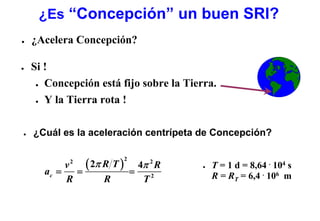
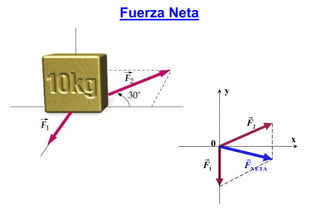
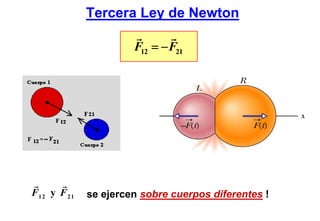
Este documento resume las tres leyes de Newton del movimiento y conceptos fundamentales como fuerza, masa, aceleración, sistemas de referencia inerciales, fuerzas de contacto y a distancia. Explica conceptos como fuerza peso, normal, roce estático y cinético, y presenta estrategias para resolver problemas usando las leyes de Newton.







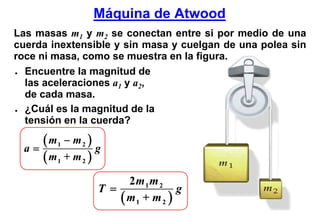
![Fuerza Peso
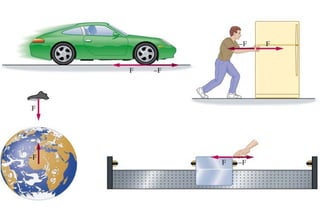
El peso de un objeto es la fuerza gravitacional que actúa
sobre el cuerpo.
Hemos visto que todos los cuerpos caen P
con la misma aceleración g por la acción
de la fuerza de gravedad:
a=g
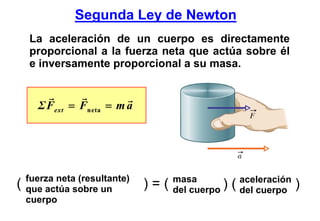
Entonces, de la 2a ley de Newton tenemos que:
g
P = mg
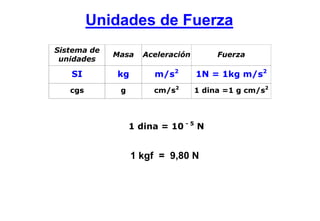
En el SI: [P] = N [m] = kg](https://image.slidesharecdn.com/cap05-120623153620-phpapp02/85/Cap05-16-320.jpg)