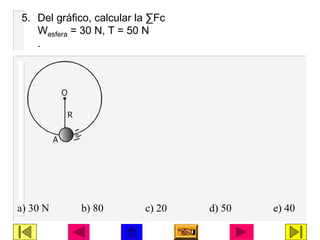
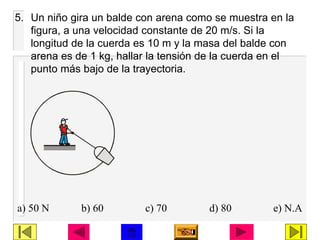
Este documento presenta información sobre dinámica lineal y circular. Explica las leyes de Newton y cómo aplicarlas para resolver problemas de dinámica lineal, incluyendo la segunda ley de Newton y el método para resolver problemas de dinámica lineal. También introduce conceptos de dinámica circular como aceleración centrípeta, fuerza centrípeta y cómo aplicar estas ideas para resolver problemas de movimiento circular. El documento contiene varios ejemplos y ejercicios de aplicación de estos conceptos.

1. Lic.ESCOBAR VARA, E. ROMMER
V
A
L
L
E
J
O
I E
C
E
S
A
R
CHANCAY

2. Te envía a la primera página
Te envía a la página anterior
Te lleva al temario
Te envía a la siguiente página
Te envía a la ultima página
Te saca de la presentación

3. 2. DINAMICA LINEAL
TEMA:
• NIVEL I
• NIVEL II
• NIVEL III
3. DINAMICA CIRCULAR
DINAMICA
1. SEGUNDA LEY DE NEWTON
• NIVEL I
• NIVEL II

4. DINAMICA
La Dinámica se constituye en la rama de la
Mecánica que se encarga de estudiar las leyes y
propiedades que explican el movimiento de los cuerpos,
a partir de las causas que la producen.

5. Segunda ley de Newton
 "Toda fuerza resultante desequilibrada que actúa
sobre un cuerpo determinado le producirá una
aceleración, será paralela con la fuerza, y resultará ser
directamente proporcional con la fuerza aplicada, pero
inversamente proporcional con la masa de dicho cuerpo".
Lo que matemáticamente se escribe así:
* Unidades en el S.I.
FR = Fuerza resultante
a = aceleración
m = masa
m a F
kg m/s2 Newton (N)
FR = m.a
F
m
a

6. 1. Se verifica si todas las unidades del problema están en
un mismo sistema.
2. Se hace el D.C.L. en cada uno de los cuerpos.
3. Se descomponen todas las fuerzas en dos direcciones:
una paralela al movimiento y otra perpendicular a él.
4. Las fuerzas perpendiculares al movimiento se anulan
entre sí, puesto que el cuerpo no se mueve en esa
dirección.
5. Las fuerzas paralelas al movimiento cumplen la segunda
ley de Newton: FR = m.a.
METODO PARA RESOLVER DINAMICA
LINEAL

7. Cómo aplicar la segunda ley de Newton?
Dado que: FR = ∑F entonces cuando se tienen sistemas
físicos que presentan varias de las fuerzas componentes
será preferible aplicar la 2da Ley de Newton en la
siguiente forma:
FR = m.a
Fuerzas a favor de "a" - Fuerzas en contra de "a" = m . a

8. Ejemplo: Hallar la aceleración con que avanza el
bloque (m = 5 kg)
2da Ley de Newton:
FR = m.a.
F1 - F2 = m . a
100 - 60 = 5 . a
a = 8 m/s2
F = 100
a
1
F = 602
N
P
Las fuerzas que son
Perpendiculares al
movimiento se anulan
P = N

9. EJERCICIOS
NIVEL I
1. Determine la aceleración del bloque (m = 8 kg.)
a) 4 m/s2 b)1,5 c) 2,0 d) 2,5 e) 3
F = 20 N

10. 2. Determine la aceleración del ladrillo (m = 4 kg.)
a) 6 m/s2 b) 9 c) 8 d) 10 e) 11
36 N 8 N

11. a)10 N b)8 c)18 d)12 e) 16
3. Determine "F" si la aceleración experimentada por el
bloque es de 4 m/s2 y su masa 6 kg.
a
F 36 N

12. 4. Determine la aceleración del bloque (m = 6 kg.)
a) 4 m/s2 b) 5 c) 6 d) 7 e) 8
12 NF=42 N
18 N

13. 5. Determine "F" si la masa es de 5 kg y la aceleración
es 3 m/s2.
a) 2 N b) 3 c) 4 d) 5 e) 1,6
3F
7F
F

14. 6. Determinar la aceleración del bloque (m = 4 kg).
a) 2 m/s2 b) 3 c) 4 d) 8 e) 10
16 N24 N

15. 7. Determine la aceleración de las masas.
a) 5 m/s2 b) 6 c) 8 d) 9 e) 7
F = 54 N 4 kg
2 kg

16. 8. Determine la masa del bloque, si adquiere una
aceleración de 3m/s2.
a) 2 b) 4 c) 6 d) 8 e) 10
24 N54 N 6
m

17. 9. Determine la aceleración del sistema.
a) 5 m/s2 b) 4 c) 10 d) 8 e) 16
F = 50 N
8 kg 2 kg

18. 10.Determine la aceleración de las masas.
a) 5 m/s2 b) 4 c) 10 d) 8 e) 16
F = 100 N
4 kg6 kg
F = 60 N

19. NIVEL II

a

a = gtan
a = gsen

20. NIVEL II
1. Determine la masa del sistema, si su aceleración es
de 5 m/s2.
a) 2 kg b) 3 c) 4 d) 5 e) 6
F = 20 N
m5
100 N
7

21. 2. Determine la aceleración si el gráfico es como sigue:
a) 3 m/s2 b) 4 c) 5 d) 7 e) 10
F = 80 N
2 kg3 kg
35 N
4 kg

22. 3. Hallar la aceleración del sistema. Datos: m1 = 5 kg,
m2 = 15 kg, m3 = 20 kg y F = 200 N
a) 4 m/s2 b) 3 c) 2 d) 5 e) 1
3
F
12

23. a) 5 m/s2 b) 2 c) 1 d) 3 e) 1,5
4. Hallar la aceleración de los bloques (g = 10m/s2),
m = 2 kg.
10m
F = 110 N
8m9m
... m

24. 5. Determine la aceleración de la caja. Si su masa es de
10kg (g = 10 m/s2)
a) 10 m/s2 b) 5 c) 4 d) 8 e) 12
F = 60 N

25. 6. Determinar la aceleración del bloque cuando baja, si su
masa es de 4 kg y F = 20 N. (g = 10 m/s2)
a) 2 m/s2 b) 3 c) 4 d) 5 e) 10
F

26. 7. Calcular la aceleración de los bloques.
a) 3 m/s2 b) 4 c) 5 d) 6 e) 7
F = 140 N
3 kg
7 kg

27. 8. Del sistema que se indica, ¿qué valor tiene la fuerza
"F"?, si el bloque de 8 kg sube con una aceleración de
valor 5 m/s2. (g = 10 m/s2)
a)100 N b)110 c)120 d)130 e) 140
F

28. 9. Para elevar verticalmente al bloque de 5 kg con una
aceleración de módulo 2 m/s2, ¿cuánta fuerza debe
aplicarse en la cuerda? (g = 10 m/s2)
a) 60 N b) 43 c) 52 d) 28 e) 42

29. 10.Un bloque de 4 kg de masa desciende con una
aceleración de 2 m/s2. Hallar la tensión en la cuerda.
(g = 10 m/s2)
a) 8 N b) 20 c) 40 d) 32 e) 60

30. NIVEL III
1. Hallar la tensión de la cuerda que une los bloques:
m1 = 9 kg; m2 = 11 kg
(g = 10 m/s2)
a) 32 N b) 34 c) 36 d) 38 e) 40
20 N 60 N
1 2

31. 2. Determine la aceleración de los bloques (mA = 8 kg;
mB = 2 kg)
a) 6 m/s2 b) 1 c) 15 d) 2 e) 5
B
A

32. 3. El sistema se abandona de la posición mostrada.
Determinar la aceleración (mA = 30 kg; mB = 10 kg;
g = 10 m/s2.)
a) 2 m/s2 b) 1 c) 3 d) 1,5 e) 2,5
A
B

33. 4. Determine la aceleración de los bloques.
a) 9 m/s2 b) 8 c) 7 d) 6 e) 5
7 kg
1 kg 2 kg
a
a

34. 5. Se tienen 2 cuerpos de masas m1 = 3 kg y m2 = 5 kg y
la fuerza de reacción entre los dos cuerpos es 20 N.
Hallar "F"..
a) 27 N b) 35 c) 48 d) 32 e) 30
F
1m
2m
m1
F 20N
m2
F = m.a
20 = 5.a a = 4 m/s2
F – 20 = 3(4)
F = 12 + 20
F = 32 N
Solución

35. 6. Del sistema mostrado, determine la tensión "T" de la
cuerda.
m
m m
T

36. 7. En la figura mostrada, hallar la tensión "T" de la cuerda,
m = 3 kg (g = 10 m/s2)
m
m
m
T

37. 8. Hallar la fuerza de contacto entre los bloques 2 y 3.
3
2 kg 3 kg 5 kg
1
2
40 N

38. 9. Hallar la fuerza "F" que se aplica al sistema sin rozamiento, si
la tensión T1 = 6 N y no existe fricción..
T
F 5 kg 3 kg 2 kg
T2 1

39. 10. De la figura, calcular la aceleración "a".
m
2m
m
a

40. DINAMICA CIRCULAR.

41. DINAMICA CIRCULAR.
Es la rama de la Mecánica, que utilizando la segunda ley de
Newton, estudia y describe el movimiento curvilíneo de las
partículas, y en particular el movimiento circunferencial.
ACELERACIÓN CENTRÍPETA (aC)
Se le suele llamar también aceleración central, o radial, y viene a
ser aquella aceleración que, sin afectar el módulo de la velocidad
tangencial, le cambia su dirección continuamente, actuando de
manera perpendicular a aquel, y orientada en todo momento
hacia el centro de curvatura.

42.  𝑎 𝑐 =
𝑣2
𝑟
Se verifica que el cambio de dirección es brusco, y por tanto la
aceleración centrípeta es grande cuando el móvil dispone de una
gran velocidad tangencial, y también cuando el radio de curvatura
es pequeño. De este modo se deduce que: "La aceleración
centrípeta es directamente proporcional con el cuadrado de la
velocidad tangencial e inversamente proporcional con el radio de
curvatura".
Vt
Vt
ac
0
w
r

43. FUERZA CENTRÍPETA (FC)
Se le llama también fuerza central o radial, y viene a ser la
componente de la fuerza total que afecta a un cuerpo en
movimiento curvilíneo, y cuya dirección se ubica sobre el
eje radial, apuntando siempre hacia el centro de la curva,
y es quien se encarga de producir la aceleración
centrípeta. Así, por la 2da ley de Newton tendremos:
FC = ∑Fradiales
FC = m ac = = mw2 r
m ac = ∑Fradiales van al centro - ∑Fradiales salen del centro
0
r
ejeradial
eje
tangencial
Ft
FT
FC
m
𝑚
𝑣2
𝑟

44. ILUSTRACIÓN: Analizaremos el movimiento de una
partícula que gira por acción de una cuerda.
* En el punto "A"
FC = mg + TA
* En el punto "B"
FC = TB
* En el punto "C"
FC = TC - mg
Observación: Si un cuerpo gira en una circunferencia, uniformemente;
la resultante de todas las fuerzas aplicadas a éste necesariamente está dirigida
hacia el centro y le comunica al cuerpo la aceleración centrípeta.
mg
TB
TA
TC
A
B
C
mg
mg

45. EJERCICIOS
1. Se hace girar una piedra en un plano vertical.
Cuando pasa por el punto "A" tiene una velocidad de
10 m/s, en "B" tiene una velocidad de 15 m/s y en
"C", 20 m/s. Calcular la tensión en A, B y C,
sabiendo que m = 4kg y R = 2m.
A
B
C

46. RESOLUCIÓN.
Resolución
En el punto "A"
F = mg + T
= mg + T
T = - mg
C
mv
R
2
A
A
A
mv
R
2
A
TC mg
A
C
mg
mg TB
TA
Reemplazando datos
En el punto "B" TA = 160 N
FC = TB
TB = En el punto "C"
TB = 450 N TC - mg = FC
TC = + mg
TC = 840 N
R
mv2
B

47. 2. Un ciclista ingresa a una pista circular, ¿qué velocidad debe tener
en el punto más alto, para que en ese momento esté por
desprenderse de la pista? R = 1,6 m.
Resolución:
Para que el ciclista se encuentre a punto de desprenderse, N = 0
FC = mg + N
FC = mg + 0
= mg
v = =
v = 4 m/s
R
mv2
gR 10(1,6)
N
mg

48. .
Resolución:
Para que el aceite se encuentre a punto de caer, la cuerda tendrá que
estar colgada (casi arrugada), T = 0.
FC = mg + T
FC = mg + 0
= mg
v = =
v = = 3,15
v = 3,15 m/s
3. Un joven hace girar un balde lleno de aceite en un plano vertical
mediante una cuerda de 1 m de longitud. ¿Cuál debe ser la
velocidad en el punto alto, como mínimo, para qué el aceite no
caiga?
R
mv2
gR )1(10
mg
T

49. 4. Del gráfico, calcular la ∑Fc
Wesfera = 20 N, T = 10 N
.
a) 10 N b) 30 c) 40 d) 50 e) 15
O
R
A

50. 5. Del gráfico, calcular la ∑Fc
Wesfera = 30 N, T = 50 N
.
a) 30 N b) 80 c) 20 d) 50 e) 40
O
R
A

51. 6. Del gráfico, calcular la ∑Fc
Wesfera = 50 N, T = 40 N
.
a) 50 N b) 40 c) 90 d) 10 e) 45
O
R
A

52. 7. Del gráfico, calcular la ∑Fc
Wesfera = 20 N, T = 30 N
.
a) 20 N b) 50 c) 40 d) 30 e) 10
O
R
B

53. 8. la masa del cuerpo realiza un movimiento circular
(m = 10 kg) con una Vt = 4 m/s, calcular la ∑Fc .
Si R = 2m
a) 40 N b) 80 c) 50 d) 60 e) 160
O
R
B

54. 9. la masa del cuerpo realiza un movimiento circular
(m = 10 kg) con una Vt = 4 m/s, calcular la ∑Fc .
Si R = 4m
a) 20 N b) 40 c) 60 d) 80 e) 50
O
R
B

55. 10.Calcular la tensión de la cuerda, si la masa del
cuerpo que realiza un movimiento circular es de 1
kg y gira con una Vt = 8 m/s. Si R = 2 m
a) 32 N b) 22 c) 42 d) 52 e) 62
O
R
A

56. NIVEL II
a) 150 N b) 160 c) 170 d) 180 e) N.A
1. La esferita mostrada es de 2kg y gira en un plano vertical
de radio 5 m y con velocidad angular: w = 4 rad/s. Hallar
la tensión de la cuerda cuando la esferita está pasando
por el punto (A).
w R=5 m
(B)
(C)
(A)

57. a) 72 N b) 40 c) 112 d) 122 e) 142
2. La esferita mostrada es de 4 kg y gira en un plano
vertical de radio 2m y con velocidad angular: w = 3 rad/s.
Hallar la tensión de la cuerda cuando la esferita esté
pasando por el punto (A).
w R=2 m
(B)
(C)
(A)

58. 3. Una esferita de 5 kg se hace girar atada de una cuerda,
describiendo una circunferencia en el plano vertical de
radio 5 m y manteniendo siempre una rapidez de
V = 10m/s. Hallar la tensión de la cuerda cuando la
esferita está pasando por (A).
a) 20 N b) 50 c) 80 d) 100 e) 150
w R=5 m
(B)
(C)
(A)
V = 10 m/s

59. 4. La esferita mostrada se suelta en (A) y tiene 8 kg.
Calcule la tensión de la cuerda cuando la esferita
pase por el punto más bajo de su trayectoria con
V = 5 m/s.
a) 10 N b) 120 c) 130 d) 140 e) N.A
L = 4 m

60. 5. Un niño gira un balde con arena como se muestra en la
figura, a una velocidad constante de 20 m/s. Si la
longitud de la cuerda es 10 m y la masa del balde con
arena es de 1 kg, hallar la tensión de la cuerda en el
punto más bajo de la trayectoria.
a) 50 N b) 60 c) 70 d) 80 e) N.A

61. 4. La esferita mostrada se suelta en (A) y tiene 8 kg.
Calcule la tensión de la cuerda cuando la esferita
pase por el punto más bajo de su trayectoria con
V = 5 m/s.
a) 10 N b) 120 c) 130 d) 140 e) N.A
L = 4 m

62. 6. Un auto de 1 000 kg va con velocidad: V = 10 m/s y pasa
por un puente en forma de semicircunferencia de radio
20 m. ¿Cuánto valdrá la normal de la superficie cuando
el auto esté pasando por el punto más alto?
a) 1000 N b) 2000 c) 3000 d) 5000 e) N.A
R

63. 7. En la figura mostrada se tiene un motor cilíndrico de radio
R = 1 m. ¿Con qué velocidad angular debe girar el motor
para que el bloque de masa 10 kg no resbale
verticalmente de la pared del cilindro cuyo coeficiente de
fricción m = 1/10 (g = 10m/s2)?
a) 10 rad/s b) 20 c) 30 d) 40 e) N.A
w
10 kg
w

64. 7. Determinar la fuerza centrípeta si el peso del bloque es
10N , la tensión de la cuerda 5N (g = 10m/s2)?
a) 13N b) 20 c) 30 d) 40 e) N.A
53°

65. GRACIAS