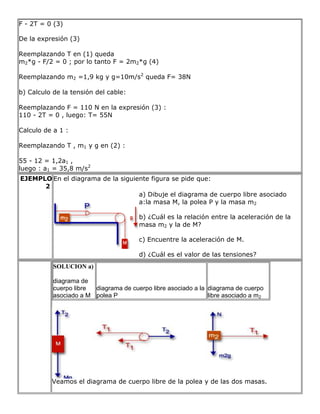
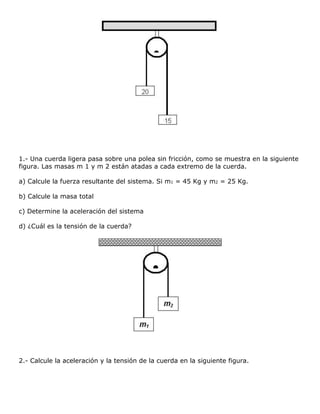
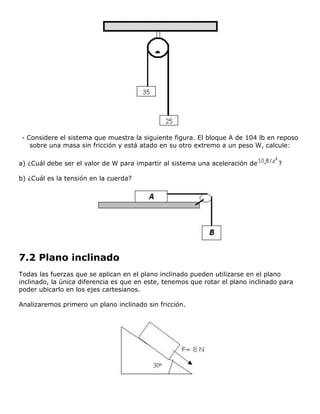
El documento resume la segunda ley de Newton. Explica que la fuerza neta aplicada a un cuerpo es proporcional a su aceleración, donde la constante de proporcionalidad es la masa del cuerpo. También introduce la cantidad de movimiento y explica cómo la segunda ley se puede expresar en términos de variaciones en la cantidad de movimiento. Finalmente, presenta algunos ejemplos de aplicación.

1. 7-1 – SEGUNDA LEY DE NEWTON
OBJETIVO:
El alumno será capaz de construir un diagrama de cuerpo libre que
represente todas las fuerzas que actúan sobre un objeto que se
encuentra en equilibrio traslacional.
La Segunda ley de Newton se encarga de cuantificar el concepto de fuerza. Nos dice
que la fuerza neta aplicada sobre un cuerpo es proporcional a la aceleración que
adquiere dicho cuerpo. La constante de proporcionalidad es la masa del cuerpo, de
manera que podemos expresar la relación de la siguiente manera:
F=m*a
Tanto la fuerza como la aceleración son magnitudes vectoriales, es decir, tienen,
además de un valor, una dirección y un sentido. De esta manera, la Segunda ley de
Newton debe expresarse como:
F=ma
La unidad de fuerza en el Sistema Internacional es el Newton y se representa por N .
Un Newton es la fuerza que hay que ejercer sobre un cuerpo de un kilogramo de
masa para que adquiera una aceleración de 1 m/s2 , o sea,
1 N = 1 Kg · 1 m/s2
La expresión de la Segunda ley de Newton que hemos dado es válida para cuerpos cuya
masa sea constante. Si la masa varia, como por ejemplo un cohete que va quemando
combustible, no es válida la relación F = m · a. Vamos a generalizar la Segunda ley de
Newton para que incluya el caso de sistemas en los que pueda variar la masa.
Para ello primero vamos a definir una magnitud física nueva. Esta magnitud física es
la cantidad de movimiento que se representa por la letra p y que se define como el
producto de la masa de un cuerpo por su velocidad, es decir:
p=m·v
La cantidad de movimiento también se conoce como momento lineal. Es una magnitud
vectorial y, en el Sistema Internacional se mide en Kg·m/s. En términos de esta nueva
magnitud física, la Segunda ley de Newton se expresa de la siguiente manera:
La Fuerza que actúa sobre un cuerpo es igual a la variación temporal de la cantidad de
movimiento de dicho cuerpo, es decir
F = d p /dt

2. De esta forma incluimos también el caso de cuerpos cuya masa no sea constante. Para
el caso de que la masa sea constante, recordando la definición de cantidad de
movimiento y que como se deriva un producto tenemos:
F = d (m· v)/dt = m·d v /dt + dm/dt · v
Como la masa es constante
dm/dt = 0
Y recordando la definición de aceleración, nos queda
F = m.a
Tal y como habíamos visto anteriormente.
Otra consecuencia de expresar la Segunda ley de Newton usando la cantidad de
movimiento es lo que se conoce como Principio de conservación de la cantidad de
movimiento. Si la fuerza total que actúa sobre un cuerpo es cero, la Segunda ley de
Newton nos dice que:
0 = dp /dt
Es decir, que la derivada de la cantidad de movimiento con respecto al tiempo es cero.
Esto significa que la cantidad de movimiento debe ser constante en el tiempo (la
derivada de una constante es cero). Esto es el Principio de conservación de la
cantidad de movimiento: si la fuerza total que actúa sobre un cuerpo es nula, la
cantidad de movimiento del cuerpo permanece constante en el tiempo.
EJEMPLOS
Calcular la aceleración que produce una fuerza de 5 N a un cuerpo cuya masa es de
1000g
Expresar el resultado en m/s².
DATOS FÓRMULA SUSTITUCIÓN RESULTADO
A=? a = F / m a = 5 Kg m/s² / 2 Kg = 2.5 m/s²
F=5N
m = 2000g = 2Kg

3. Calcular la masa de un cuerpo si al recibir una fuerza de 200N le produce una
aceleración de 300 cm/s². Exprese el resultado en Kg.
DATOS FÓRMULA SUSTITUCIÓN RESULTADO
M=?
F = 200 N a=f/m
A = 300 cm/s² = 3 m/s² m=f/a m = 200N / 3 m/s² = 66.6 Kg
EJEMPLO 1 Una fuerza F se ejerce directamente hacia arriba sobre el eje de la polea sin
masa. Considere que la polea y el cable carecen de masa. Dos objetos, de
masas m 1 = 1,2 kg m 2 = 1,9 kg, están unidos a los extremos opuestos del
cable, el cual pasa por la polea. El objeto m 2 está en contacto con el piso.
a) ¿Cuál es el valor más grande que la fuerza F puede tener de modo que m 2
permanezca en reposo sobre el piso?
b) ¿Cuál es la tensión en el cable cuando la fuerza F hacia arriba sea de 110
N? ¿Cuál es la aceleración de m 1?
SOLUCION
Veamos el diagrama de cuerpo libre de la polea y de las dos masas.
a) Para que m2 permanezca en reposo sobre la superficie, debe ser mayor que m1.
Fuerzas sobre m2:
m1*g - T - N = 0,
pero N = 0 cuando está a punto de despegar.
Luego: m2*g - T = 0 (1)
Fuerzas sobre m 1:
T - m1*g = m1* a1 (2),
donde es la aceleración con que sube. Aquí existe una aceleración, porque si la masa 2
tiene que estar en reposo y la cuerda es inextensible, obvio que la masa m1 se mueve.
Fuerzas sobre la polea:

4. F - 2T = 0 (3)
De la expresión (3)
Reemplazando T en (1) queda
m2*g - F/2 = 0 ; por lo tanto F = 2m2*g (4)
Reemplazando m2 =1,9 kg y g=10m/s2 queda F= 38N
b) Calculo de la tensión del cable:
Reemplazando F = 110 N en la expresión (3) :
110 - 2T = 0 , luego: T= 55N
Calculo de a 1 :
Reemplazando T , m1 y g en (2) :
55 - 12 = 1,2a1 ,
luego : a1 = 35,8 m/s2
EJEMPLO En el diagrama de la siguiente figura se pide que:
2
a) Dibuje el diagrama de cuerpo libre asociado
a:la masa M, la polea P y la masa m2
b) ¿Cuál es la relación entre la aceleración de la
masa m2 y la de M?
c) Encuentre la aceleración de M.
d) ¿Cuál es el valor de las tensiones?
SOLUCION a)
diagrama de
cuerpo libre diagrama de cuerpo libre asociado a la diagrama de cuerpo
asociado a M polea P libre asociado a m2
Veamos el diagrama de cuerpo libre de la polea y de las dos masas.

5. b)
Por lo tanto:
Otra forma de ver, es que si la masa M se mueve X, la m2 se mueve X/2. Si
hacemos la derivada de la posición dos veces, obtenemos la aceleración de las
masas y llegamos a la misma relación.
c) Según diagrama de cuerpo libre, se tiene:
(1) T 1 = m2*a2
(2) M*g= M*aM
(3) T2 - 2T1 =0
Además sobre m2: N - m2*g= 0,
ya que no hay movimiento en ese eje.
Reemplazando (1) en (3) , se tiene: T2 - 2m2* a2 = M*aM (4)
Reemplazando (4) en (2) , se tiene:
M*g - 2m* a2 = M*aM pero, a2 = 2*aM
M*g - 2m2* a2 = M*aM
M*g = (M + 4m 2 )*aM, entonces:

6. d) Reemplazando en expresión a 2 = 2aM en expresión (1) , se
obtiene
:
T1 = m2*aM , por lo tanto:
de la expresión ( 3) , T2 = 2T1 , por lo tanto reemplazando el valor obtenido
EJEMPLO 3
Considere el sistema que muestra la siguiente figura. El bloque A de 64lb en reposo
sobre una masa sin fricción y está atado en su otro extremo a un peso W, calcule:
a) ¿Cuál debe ser el valor de W para impartir al sistema una aceleración de ?
b) ¿Cuál es la tensión en la cuerda?
SOLUCIÓN (a)
Dibuje el diagrama cuerpo libre (boton diagrama cuerpo libre)

7. Puesto que las fuerzas verticales en el bloque de 64lb están equilibradas, la fuerza neta
en el sistema total es solo el peso W. Aplicamos la ley de Newton:
2W=64lb+W
2W – W = 64lb
w=64lb
SOLUCIÓN (b)
T= 32lb
ACTIVIDAD No.2
Calcule la aceleración y la tensión de la cuerda en la siguiente figura.

8. TAREA 2
Una cuerda ligera pasa sobre una polea sin fricción, como se muestra en la siguiente
figura. Las masas m 1 y m 2 están atadas a cada extremo de la cuerda.
a) Calcule la fuerza resultante del sistema. si m 1 = 15 Kg y m 2 = 8 Kg.
b) Calcule la masa total
c) Determine la aceleración del sistema
d) ¿Cuál es la tensión de la cuerda?
Calcule la aceleración y la tensión de la cuerda en la siguiente figura.

9. 1.- Una cuerda ligera pasa sobre una polea sin fricción, como se muestra en la siguiente
figura. Las masas m 1 y m 2 están atadas a cada extremo de la cuerda.
a) Calcule la fuerza resultante del sistema. Si m1 = 45 Kg y m2 = 25 Kg.
b) Calcule la masa total
c) Determine la aceleración del sistema
d) ¿Cuál es la tensión de la cuerda?
2.- Calcule la aceleración y la tensión de la cuerda en la siguiente figura.

10. - Considere el sistema que muestra la siguiente figura. El bloque A de 104 lb en reposo
sobre una masa sin fricción y está atado en su otro extremo a un peso W, calcule:
a) ¿Cuál debe ser el valor de W para impartir al sistema una aceleración de ?
b) ¿Cuál es la tensión en la cuerda?
7.2 Plano inclinado
Todas las fuerzas que se aplican en el plano inclinado pueden utilizarse en el plano
inclinado, la única diferencia es que en este, tenemos que rotar el plano inclinado para
poder ubicarlo en los ejes cartesianos.
Analizaremos primero un plano inclinado sin fricción.

11. Donde W = 3 N
Rotación del eje:
Paso 1
Σ Fx = 0
Σ Fy = 0
Σ Fx = Fa + W Cos 60º = 0
Σ Fy = Fn – W sen 60º = 0
EJEMPLO
Un niño sostiene un trineo en reposo en la ladera de una colina de 27° cubierta de nieve
y sin fricción. Si el trineo pesa 77 N, determine la fuerza que el niño ejerce sobre el
trineo.

12. Rotación del eje:
Σ Fx = -Fa + W Cos 63º
Σ Fy = Fn – Wsen 63º
Despejando
Fa = W Cos 63 o = 77 N Cos 63º = 34.95 N
Fn = W Sen63 o = 77 N Sen 63 o = 68.6 N
ACTIVIDAD 1
1.- Un niño jala su carrito a través de una pendiente inclinada 17°. Si el carrito pesa 25
N, ¿con qué fuerza debe jalar el pequeño para subir su carrito con velocidad constante?
2.- Un hombre empuja una maleta a lo largo de plano inclinado 35°. Si la fuerza de
empuje es de 300 N,
a) ¿Cuál es el peso de la maleta?
b) ¿Cuánto vale la fuerza normal?

13. 3.- Usted empuja hacia arriba por un plano inclinado 20° un baúl de 325 N con
velocidad constante, ejerciendo una fuerza de 211 N paralela al plano inclinado.
a) ¿Cuál es la componente del peso del baúl paralela al plano?
b) ¿Cuál es la fuerza normal?
7.3 Plano inclinado con Fricción.
La fricción es la fuerza que se opone el movimiento y tiene muchas aplicaciones como
pudimos observar en el capítulo anterior.
Formulas
Ff = Fn μ
Fn = W Sen α
EJEMPLO
Una caja de 100 N reposa sobre un plano inclinado 30° .Si el coeficiente de fricción es m
= 0.1. ¿Cuál es la fuerza de empuje paralela al plano necesario para subir el plano con
velocidad constante?
Rotación del eje:

14. Σ Fx = -Fa + W Cos 60º + Ff = 0
Σ Fy = Fn – W sen 60º = 0
Despejando:
Fn = W Sen 60º = 100 N Sen 60º = 86.6 N
Ff = Fn μ = 86.6 N (0.1) = 8.66 N
Fa = W Cos 60º + Ff = 100 N Cos 60º + 8.66 = 58.66 N
ACTIVIDAD 2
1.- Una caja de madera de 215 N se desliza hacia debajo de un plano inclinado de 45°.
El coeficiente de fricción cinética es 0.12.
a) ¿Cuál es la fuerza normal sobre el bloque?
b) ¿Cuál es la fuerza de fricción cinética?
c) ¿Cuál es la fuerza resultante?
d) ¿Cuál es la aceleración?
TAREA 1
1.- ¿Cuál es el empuje necesario para subir un bloque de 70 Kg sobre un plano inclinado
55°? No considere la fricción.
2.- Un hombre empuja, con velocidad constante, una caja de 320 N por un plano
inclinado 25° ejerciendo una fuerza paralela al plano de 150 N. ¿Cuál es la fuerza
normal? (Suponga que no hay fricción entre la caja y el plano inclinado).
4.- ¿Cuál es la fuerza mínima necesaria para mantener en reposo un bote de remos de
240 N en la ladera de una colina inclinada 27° ¿Cuál es la fuerza normal? (Suponga que
no hay fricción entre la colina y el bote).