Este documento presenta una introducción a conceptos fundamentales de energía eléctrica. En la primera sección se describen diferentes formas de energía como mecánica, química, térmica y eólica. La segunda sección explica que la energía eléctrica está relacionada con el movimiento de electrones y puede describirse mediante mecánica y mecánica cuántica. Finalmente, se presenta el modelo atómico de Bohr para explicar cómo la estructura atómica y el comportamiento de los electrones están relacionados con la energ

1. TABLA DE CONTENIDO
1. INTRODUCCION ............................................................................................. 7
1.1. Formas de energía ................................................................................................ 8
1.2. Energía eléctrica ................................................................................................. 10
1.3. Transporte de energía eléctrica: ........................................................................ 12
1.4. Conductividad en los materiales: ...................................................................... 14
1.5. Notación científica .............................................................................................. 15
1.6. Corriente .............................................................................................................. 17
1.7. Voltaje .................................................................................................................. 19
2. RESISTENCIAS ............................................................................................. 26
2.1 Resistividad .......................................................................................................... 28
2.2. Resistencia .......................................................................................................... 28
2.2.1. Ley de OHM ...................................................................................................... 30
2.3. Resistencia eléctrica ........................................................................................... 31
2.3.1. Definiciones y símbolo ................................................................................... 35
2.4. Código de colores ............................................................................................... 36
3. ASOCIACIÓN DE RESISTENCIAS ............................................................... 42
configuraciones ......................................................................................................... 43
3.2 Cálculos en circuitos resistivos ......................................................................... 45
3.2.1. Circuito serie: ................................................................................................... 45
3.2.1.2. Otros cálculos en circuitos resistivos serie ............................................... 47
3.2.2 Circuito paralelo: ............................................................................................... 50
3.2.3. Circuito mixto: ................................................................................................. 55
4. USO DEL SOFTWARE DE SIMULACIÓN CIRCUIT MAKER ....................... 61
4.1. Simulación con Circuit Maker y Multisim .......................................................... 62
5. USO DE INSTRUMENTOS ............................................................................ 71
5.1 El Protoboard ....................................................................................................... 72
5.2 El cautín ................................................................................................................ 73
5.3 El Multímetro ........................................................................................................ 74
6. CONDENSADORES ...................................................................................... 80
6.1. Principios físicos ................................................................................................ 81
6.2. Clasificación de condensadores ........................................................................ 84
6.2.1. Variables: .......................................................................................................... 85

2. 6.2.2. Fijos: ................................................................................................................. 86
6.2.2.1. Polarizados: ................................................................................................... 86
6.2.2.2 No polarizados: .............................................................................................. 87
6.3. Medición .............................................................................................................. 88
6.3.1. Determinación por nomenclatura .................................................................. 89
6.3.2. Determinación por instrumento ..................................................................... 92
6.4. Comportamiento en AC Y DC ............................................................................. 93
6.4.1. Comportamiento en AC: .................................................................................. 93
6.4.2. Comportamiento en DC: .................................................................................. 95
6.5 REACTANCIA CAPACITIVA ................................................................................. 99
7. CONDENSADORES EN SERIE, PARALELO Y MIXTO ............................. 103
7.1. Asociación de condensadores ......................................................................... 105
7.1.1 SERIE: .............................................................................................................. 105
7.1.2. Paralelo: .......................................................................................................... 107
7.1.3. Mixto: .............................................................................................................. 109
7.2. Manejo de instrumentos: .................................................................................. 110
7.2.1. El generador de señales y el osciloscopio ................................................... 110
8. BOBINAS ..................................................................................................... 115
8.1 Principios y definición ....................................................................................... 116
8.2 Clasificación de bobinas ................................................................................... 118
8.3. Códigos ............................................................................................................. 119
8.3.1. Determinación por nomenclatura ................................................................ 119
8.3.2. Determinación por instrumento .................................................................... 121
8.4. Comportamiento en AC Y DC ........................................................................... 122
8.4.1. Reactancia inductiva ...................................................................................... 123
8.5. Asociación de bobinas ..................................................................................... 123
8.5.1. Serie: ............................................................................................................... 124
8.5.2. Paralelo: .......................................................................................................... 124
8.5.3. Mixto: .............................................................................................................. 125
8.6. El transformador ............................................................................................... 126
8.6.1. Principio de funcionamiento ......................................................................... 127
MAPA CONCEPTUAL DE LA MATERIA

3. COMPETENCIAS GENERALES
Competencia cognitiva:
Aplica los principios básicos en el análisis y diseño de circuitos con elementos pasivos, realizando la comprobación de éste a partir del software de simulación Circuit Maker.
Identifica los parámetros a tener en cuenta, en la selección de un semiconductor para una aplicación en contexto, a partir de las curvas características.
Competencia comunicativa:
Presenta en forma correcta, adecuada y coherente, los informes de laboratorio y demás trabajos escritos, sugeridos por el docente.
Competencia valorativa:
Trabaja en equipo con un alto grado de compromiso y responsabilidad frente a las tareas asignadas en los diferentes roles a desempeñar en la dinámica de éste.

4. Competencia contextual:
Diseña e implementa una fuente de voltaje regulada a partir de las especificaciones sugeridas por el docente.
INTRODUCCION
En el presente documento, se plantea una estrategia para adquirir los conocimientos suficientes y necesarios establecidos para la materia de Electrónica Básica, propuestos para la Corporación Internacional para el Desarrollo Educativo (CIDE). La estructura fundamental del documento está planteada bajo el constructivismo y aprendizaje significativo, esta metodología, requiere que el estudiante realice cada una de las actividades que se plantean y profundice donde sea necesario, usando los recursos que para tal fin la institución pone a su disposición.
La estructura de cada unidad inicia con el repaso de algunos conceptos básicos, fundamentales para el desarrollo de los diferentes conceptos, posteriormente se hace una explicación de cada uno de ellos, referenciando las teorías básicas, necesarias para la comprensión de éstos, en los “Ladillos” se hacen explicaciones específicas sobre conceptos o palabras que aparecen y que son necesarias para la interpretación inmediata del texto, cabe aclarar que no es suficiente con esto, pues el estudiante debe realizar donde sea necesario y pertinente un repaso detallado de algunos conceptos; las actividades complementarias, refuerzan los conceptos tratados en cada unidad y permiten al estudiante una profundización y autoevaluación.
Al finalizar encontrará una sección denominada Nexos, la cual está enfocada hacia la conexión entre la unidad tratada y las subsiguientes. En la bibliografía recomendada, se plantean los recursos didácticos y documentos para el desarrollo y comprensión de cada uno de los temas, el estudiante, puede hacer una revisión

5. de ésta antes de iniciar el estudio de la unidad, recopilar la información necesaria es importante, pues tenerla a la mano hace que se ahorre tiempo en cada una de las actividades y practicidad al tratar cada uno de los temas. Finalmente, se plantea una evaluación final o seguimiento del auto aprendizaje, el cual busca que cada uno revise si los diferentes conceptos quedaron comprendidos o si es necesario hacer revisión de éstos; una propuesta al respecto sugiere que realice otra actividad complementaria si es necesario el refuerzo de algún concepto, planteada por su maestro.
Muchos éxitos en el estudio de esta área fundamental de la electrónica y recuerde que la aprehensión del conocimiento debe ser un elemento fundamental en el desarrollo conceptual de ésta y otras materias, entendido como el apropiación del conocimiento de manera consciente y autónoma, enmarcado en la motivación personal y el interés de adquirir los conocimientos necesarios para el buen desempeño en su rol como futuro profesional.
CONCEPTOS PREVIOS:
Antes de empezar el fascinante estudio de la electrónica, se hace necesario que se repase algunos conceptos básicos sobre la física, a continuación se presenta un cuestionario el cual puedes contestar usando la bibliografía sugerida.
1. ¿Qué es medición y cuál es la diferencia con la acción de medir?
2. ¿Qué es un patrón de medida y un sistema de medida?
3. ¿Cómo se determina la velocidad de un cuerpo, desde la física y cuáles son las variables que intervienen?
4. ¿Qué es aceleración y cuál es la relación con la velocidad?
5. Busca el concepto de masa y explícalo con tus propias palabras
6. ¿puede una persona realizar un trabajo si está no está en movimiento? Explica tu respuesta.
7. En un libro de física de los sugeridos, lee el concepto de energía, realizando un mapa conceptual, según éste realiza un listado de las

6. formas de energía que conoces y compáralas con las que encuentres en Internet.
8. ¿Cuáles son los principios de la termodinámica?, ¿Cómo y cuál crees que se aplica en la producción de energía térmica?
9. Busca la teoría de la relatividad e identifica el concepto de energía, la relación que ésta tiene con la velocidad y compáralo desde la mecánica (Energía potencial y energía cinética), realiza un paralelo entre los dos conceptos.
10. Según la tercera ley de Newton, escriba con sus propias palabras dicho concepto y realice una revisión del concepto de fuerza.

7. MODULO 1
1. INTRODUCCION
INTRODUCCIÓN
En éste capítulo, se encuentran algunos conceptos previos necesarios para la comprensión de los diferentes temas a lo largo del curso, se debe tener especial cuidado en la comprensión del concepto de energía, pero específicamente en el de energía eléctrica.
El transporte y aprovechamiento de éste tipo de energía, ha hecho que se desarrollen avances en ciencia y tecnología, la base fundamental que ha permitido este tipo de desarrollo dentro del estudio de la energía eléctrica, ha sido la física y su lenguaje de comunicación y construcción teórica: la matemática, por ello se encuentran algunos conceptos desde dichos puntos de vista, es necesario familiarizarse con ellos y repasar los conceptos, necesarios para la buena comprensión de los temas siguientes.
El desempeño en ésta unidad está ligado a la dedicación que se tenga en relación con la comprensión de dichos temas, por ello se debe realizar una lectura concienzuda de cada uno de ellos y resolver cualquier inquietud que se presente, por muy trivial que parezca.
MAPA CONCEPTUAL

8. LOGROS:
 Identifica las características eléctricas de la materia y su clasificación
 Reconoce las diferentes formas de energía y su esquema general en la forma de producción
 Reconoce las características eléctricas de la materia y su aplicación al transporte de energía.
 Clasifica la energía eléctrica según su forma de producción y transmisión.
 Identifica los conceptos de Alterno y Directo en los efectos de la energía eléctrica.
1.1. FORMAS DE ENERGÍA
“La energía no se crea ni se destruye, solo se transforma”, principio de conservación de la energía, según el primer principio de la termodinámica. La ley de la relatividad, plantea que cualquier sistema que tiene masa, tiene energía. Para el estudio de la electrónica, la energía que se manipula es la energía eléctrica, la cual se obtiene de diferentes formas. Para producir
QUIMICA
SEMICONDUCTORES
NO
METALES
AISLANTES
METALES
CONDUCTORES
CLASIFICACIÓN
DE
MATERIALES
CORRIENTE
VOLTAJE
TRANSPORTE
ENERGIAS
ALTERNATIVAS
TERMOELECTRICAS
HIDROELETRICAS
PRODUCCION
ELECTRICA
CINETICA
ENERGIA
POTENCIAL
EOLICA
TERMICA
DINAMICA

9. energía el hombre ha descubierto innumerables formas, según éstas, la energía puede ser:
Mecánica: La que se da debido al movimiento y puede ser:
Cinética: Debida al movimiento. A medida que un cuerpo se mueve aumenta su energía cinética.
Potencial: Obtenida con respecto a la posición en un sistema, por ejemplo si levantamos un objeto, antes de dejarlo caer de su posición inicial, tiene una energía potencial, la cual fue impresa al levantarlo y por acción de la gravedad.
Química: En ella intervienen reacciones químicas debido a la combinación de compuestos, cuando se fabrican baterías se combinan dos compuestos químicos con propiedades especiales, hay desbalance en la cantidad de electrones, haciéndolos uno más negativo que otro.
Térmica: Es aquella que se presenta en los procesos donde hay intercambio de calor.
Eólica: Interviene el viento como generador de energía a partir de mecanismos que generan energía por su movimiento.
Se puede hacer otra clasificación dependiendo del sistema físico bajo el cual se analice.
APRENDIZAJE COLABORATIVO:
Actividad:

10. Se sugiere hacer lectura del texto encontrado en el enlace: http://es.wikipedia.org/wiki/Energ%C3%ADa o al concepto sobre energía que se encuentra en el libro: Física de Holliday. HOLLIDAY, David y Equipo. Fundamentos de Física. Sexta Edición, Volumen I; Capítulo 7 pag. 136. Socialice con sus compañeros y realice un mapa conceptual.
1.2. ENERGÍA ELÉCTRICA
La energía eléctrica, independiente del modo o la forma como se obtenga, está relacionada con los electrones y su movimiento, dicho fenómeno se puede describir mediante las teorías del movimiento de partículas, desde la mecánica, combinándose con algunas teorías de la mecánica cuántica.
Ladillo:
La parte de la física que estudia el movimiento de partículas “grandes” desde las leyes de Newton se conoce como Física clásica o mecánica; la parte de la física que estudia el movimiento de partículas “pequeñas”, se denomina Física cuántica, las dos difieren pues las predicciones en una no se dan en la otra. La Mecánica cuántica relativista tiene en cuenta las leyes de la relatividad propuestas por Albert Einstein.
El poder controlar la energía eléctrica ha hecho que avancemos en tecnología, para ello se han desarrollado un sinnúmero de elementos que se conectan entre sí formando un circuito, el circuito permite a partir de la energía eléctrica una gama de posibilidades, que al combinarse cumplen con una función específica, más adelante se profundizará en el tema.
La energía eléctrica se puede interpretar si se tiene clara la estructura atómica de la materia y su comportamiento. Un átomo está conformado por un núcleo en el cual aparecen Neutrones y Protones como partículas fundamentales, en la periferia alrededor del núcleo se encuentran los Electrones, los cuales están más cerca o menos cerca del núcleo según su energía, hay muchos modelos

11. atómicos, sin embargo el más aceptado es el de Bohr, el cual se representa a continuación:
Figura 1.2.1 Modelo atómico de Bohr
Tomado de: http://es.wikipedia.org/wiki/Modelo_at%C3%B3mico_de_Bohr, Diciembre de 2009
En la Figura 1.2.1 se observa el modelo del átomo, ésta no es una representación real de un átomo, es decir no es la “foto” del átomo, si no el modelo que permite explicar cómo funciona un átomo. Los electrones pasan de un nivel de menor energía a otro de mayor energía y viceversa, esto hace que se presente un intercambio de energía, ya sea absorber o radiar energía, a éste tipo de energía que proviene del electrón, se le denomina energía eléctrica.
La facilidad con que un electrón pasa de un nivel a otro, depende del elemento y la reacción que se presente para ello, sin embargo el átomo obedece a una ley natural, la cual se describe a continuación:
 Ley del octeto: Todo elemento químico, tiende a completar 8 electrones en su último nivel, para ello se asocia con otros átomos, mediante enlaces llamados covalentes, si comparte electrones, o

12. iónicos si cede o “gana” electrones, cuando un átomo tiene dicha estructura se dice que hay equilibrio eléctrico.
Al intercambio de electrones se le conoce como carga eléctrica. La unidad de medida de dicha carga es el Coulomb, éste se determina por la carga que desde 1 metro ejerce sobre otra carga igual, la fuerza de 9x109 Newton´ s. Se determino experimentalmente que la carga de un electrón es de -1,602x10-19 Coulomb.
1.3. TRANSPORTE DE ENERGÍA ELÉCTRICA:
Para producir energía eléctrica, la forma más común, fueron las termoeléctricas, las cuales a partir del calor producían movimiento en un mecanismo, ésta energía mecánica es transformada en energía eléctrica, gracias a un elemento conocido como alternador, como se observa en la figura, la cual representa la estructura básica de una de ellas. En realidad hoy en día la diferencia entre una u otra forma de producir energía eléctrica, es la forma como se genera el movimiento mecánico para convertirlo en energía eléctrica, de tal forma que podemos usar: el viento para que giren unas aspas, la caída del agua para producir el mismo efecto, entre otras muchas, claro no es la única forma, se han hecho grandes descubrimientos y se ha logrado producir energía de otras maneras.
A continuación, se presenta un modelo de una termoeléctrica, la intención es que el estudiante se familiarice con la estructura de una planta productora de energía, en éste caso se usa la energía calorífica para ser transformada en energía eléctrica, la diferencia con una planta hidroeléctrica es que el movimiento del mecanismo o alternador lo hace la fuerza que se obtiene por la caída del agua, si se quiere usar la energía eólica se usa como elemento generador de movimiento, el viento y así sucesivamente, cabe aclarar que el mecanismo y la estructura en términos generales es la misma, pero que cada una tiene unos aditamentos o elementos diferentes, la explicación específica de cada una de ellas están fuera del alcance de éste texto, se recomienda, si se quiere profundizar un poco más en

13. éste tema tan interesante, consultar en las fuentes bibliográficas sobre producción de energía eléctrica.
Figura 1.3.1 Diagrama esquemático de una termoeléctrica
Tomado de: http://es.wikipedia.org/wiki/Central_termoel%C3%A9ctrica,
Hoy en día se han hecho esfuerzos ingentes para producir energía “limpia”, procurando impactar en el menor grado posible, el medio ambiente, muchos proyectos de investigación tienen su meta en éste objetivo común, debido a la concientización que se ha hecho, en torno a la conservación de nuestro medio ambiente.
Una vez descubierta la forma de producir energía eléctrica, su transporte para llevarla a los sitios donde debía utilizarse, fue el paso a seguir. Uno de los pioneros en el uso de la energía Eléctrica fue el Inventor Thomas Alba Edison, con sus inventos y descubrimientos logró hacer que la vida en la época fuera cada vez más fácil, su principal invención, la bombilla eléctrica, permitió no solo iluminar la noche. Con los avances en la ciencia y la tecnología hasta ese entonces, se sabía

14. que los mejores conductores eran los metales, éstos facilitan el paso de energía, en éste caso la eléctrica.
1.4. CONDUCTIVIDAD EN LOS MATERIALES:
La conductividad de un material se define como la facilidad que éste tiene para conducir energía, para el caso de la conductividad eléctrica, el material facilita conducir éste tipo de energía, aunque hay una estrecha relación con la conductividad de energía térmica. La unidad de medida es Siemens por metro (S/m) y se representa por la letra griega (Rho) ρ.
Un material puede ser conductor de energía eléctrica, dependiendo de los electrones que tenga en su último nivel, a éste se le conoce como nivel o banda de valencia. En el caso del cobre, material que por excelencia es usado como conductor, en el nivel de valencia, tiene 1 electrón, lo hace ideal para ceder dicho electrón.
Figura 1.4.1. Configuración electrónica de un átomo de Cobre (Cu)
Tomado de: http://es.wikipedia.org/wiki/Archivo:Atomo_di_rame.svg. Diciembre 15 de 2009
Aunque existen materiales que son mejores conductores como la plata y el oro, su aplicación en la conducción de energía eléctrica, es mínima debido a los altos

15. costos. Como se puede inferir, los mejores conductores eléctricos son los elementos metales, que se pueden observar en la tabla periódica.
Cabe aclarar que la conductividad eléctrica es diferente a la conductancia, aunque hay una relación entre dichos conceptos, en el tema sobre resistencia (Sección 2.1), se hablará de la conductancia.
1.5. NOTACIÓN CIENTÍFICA
Las variables físicas deben ser cuantificadas, para ello se usan las unidades de medida, estas mediciones se expresan mediante notación científica, la cual facilita la expresión de dichas cantidades, pues en muchas ocasiones éstas son o muy grandes o muy pequeñas. La notación científica, usa las potencias de 10 para expresar cantidades, en la siguiente tabla se presenta un resumen de su significado y la forma como se debe usar.
Tabla 1.5.1. Notación científica
Notación
Prefijo
Valor multiplicativo
109
Tera(T)
1000000000
Múltiplos
106
Mega (M)
1000000
103
Kilo(K)
1000
102
Hecto(H)
100
101
Deca(D)
10
100
Unidad
1
10-1
deci (d)
0,1
Submúltiplos
10-2
centi©
0,01
10-3
mili (m)
0,001
10-6
micro (μ)
0,000001
10-9
nano (n)
0,000000001
10-12
pico (p)
0,00000000001

16. Para usar la tabla, sin importar la unidad de medida, se multiplica por el número que se observa en la columna: valor multiplicativo o se agrega el prefijo, es válida tanto una como la otra forma de expresión. Por ejemplo, si la magnitud a medir es la distancia, como unidad de medida se usa el metro, si son distancias muy pequeñas, se usarían cantidades más pequeñas que el metro, es decir los submúltiplos, si la cantidad es muy grande, se usan los múltiplos. Por ejemplo:
 El radio del átomo de Hidrógeno es de 0,000000000025 metros (m), si observas después de la coma hay 12 cifras, si llevamos la coma desde el punto donde está hacia la derecha, hasta el final de las cifras, se escribe: 25 X 10-12 metros, también es válido escribir 25 pm (pico metros), reemplazando la potencia de 10 por su prefijo respectivo, si lo expresamos en nanómetros (nm), debemos correr la coma 9 cifras: 0,025 x 10-9 o lo que es igual 0,025 nm.
 El diámetro del sol es de 1.390.000.000 metros (m)1, la cantidad se puede expresar en notación científica fácilmente, se toma como punto de partida la última cifra y se “corre” la coma hacia la izquierda tantos espacios como corresponda al exponente de la potencia de 10, si lo hacemos 3 espacios, la cantidad queda: 1.390.000 x 103, lo que es igual a 1.390.000 Km (Kilómetros); si lo hacemos 6 espacios la cantidad se expresa: 1.390 Mm (Mega metros), aunque no es común encontrar cantidades expresadas en Mega metros, aplica para el ejemplo.
Trabajo individual:
Actividad:
Escriba las siguientes cantidades en notación científica usando la tabla:
1 Tomado de: http://sunearthday.nasa.gov/2007/materials/solar_pizza.pdf, Diciembre 29 de 2009. 9:43 am

17.  0,0012345 g (gramos) en ng (nano gramos)
 1,2343233234 m en mm (milímetros)
 1.234.453 g (gramos) en Kg (Kilogramos)
 2,345123 Kg (Kilogramos) en Hg (Hectogramos)
 2,376589 cm (centímetros) en μm (micro metros)
1.6. CORRIENTE
La corriente está definida como la cantidad de electrones por unidad de tiempo, o cantidad de carga por unidad de tiempo, que atraviesan un conductor, también se le conoce como intensidad eléctrica. La unidad básica es el Amperio, en electrónica, se trabajan con corrientes pequeñas, del orden de los miliamperios, por debajo del amperio, aunque hay aplicaciones industriales donde se puede llegar a usar corrientes entre las unidades y unos cientos de Amperios (A).
Por ejemplo, una corriente puede ser del orden del micro amperio (μA), nano Amperio (nA), etc.
 Corriente AC
La corriente AC, tiene como característica especial, una frecuencia, ésta se puede representar usando una señal seno, con lo que se agregan condiciones de frecuencia, periodo, amplitud y tiempo.
Como se observa en el siguiente gráfico:
Figura 1.6.1.1 Función Seno

18. Tomado de: http://es.wikipedia.org/wiki/Seno_(trigonometr%C3%ADa) Dic 29 de 2009 1:55pm
La amplitud es el valor máximo y mínimo que toma la función, en este caso -1 y 1 Amperios (A); el periodo es 2π que corresponde al ángulo recorrido por la función, también podemos expresar el periodo como el tiempo transcurrido en un ciclo y la frecuencia es el inverso del periodo, corresponde a los ciclos por segundo, y se da en Hertz (Hz), en éste caso es de 1 ciclo en 1 segundo, o sea 1 Hz.
La fórmula que relaciona el periodo y la frecuencia esta dad por:
Ecuación. 1.6.1.1 Frecuencia y Periodo
f = Frecuencia
T = Periodo
Si vamos al caso real, la corriente que llega a nuestras casas, puede tener amplitudes de 40 Amperios (A) y una frecuencia de 60 Hz, si observas en la parte de atrás de un electrodoméstico, encontrarás una placa con las especificaciones de con sumo de corriente y frecuencia.
 Corriente DC
La corriente en DC, como característica especial, a diferencia de la corriente AC, se representa mediante una línea recta, ya que es constante en el tiempo, no tiene frecuencia y es la que se genera en las baterías, aunque no es la

19. única fuente de corriente DC, la magnitud tampoco es una norma, pero en electrónica el orden de la corriente está entre los mA (miliamperios), μA (microamperios) y nA (nanoamperios).
Actividad individual:
Actividad 1.6.1:
Representa cada una de las siguientes corrientes según como se indica:
a. 250 mA (miliamperios) en nA (nano Amperios)
b. 500 μA (micro Amperios) en mA (miliamperios)
c. 1342 nA en μA
d. 35234 μA en mA
e. 12000 μA en nA
1.7. VOLTAJE
El voltaje también denominado potencial eléctrico, está asociado a la definición de trabajo, es la energía necesaria para mover una carga, la unidad de medida del voltaje es el voltio, el voltaje, como la corriente puede ser:
 Voltaje AC
Como se explicó anteriormente, así como la corriente, tiene propiedades de frecuencia, amplitud, periodo y tiempo, El voltaje AC, se representa mediante una señal seno. Es el voltaje que llega hasta nuestras casas mediante el servicio prestado por la empresa de energía, en cuyo caso puede monofásico, bifásico o trifásico, generalmente es monofásico, es decir una sola fase y un neutro, la fase se puede probar con un téster o buscador de polo, que se consigue en las ferreterías, éste es un destornillador de pala, el cual se coloca en el toma corriente, o toma de pared, si la luz se enciende, quiere decir que dicho terminal es la fase, si no se enciende, ésta es la tierra.

20. Figura 1.7.1.1 Probador de polo o destornillador Téster
Tomado de: http://es.wikipedia.org/wiki/Archivo:Kenden_Driver.JPG
Si se observa la fase en un osciloscopio, se vería una señal seno.
Ladillo: Un Osciloscopio es un instrumento del laboratorio de electrónica, éste consiste en una pantalla, donde al ser calibrado adecuadamente, se puede observar las señales de voltaje que se llevan al instrumento a través de una sonda, para su uso se debe tener mucho cuidado, pues de no usarse adecuadamente, se puede dañar dicho instrumento. Los osciloscopios pueden ser análogos o digitales. En la sección correspondiente, se tratará sobre su uso adecuado.
 Voltaje DC
EL voltaje DC, es el que se obtiene en una batería por el diferencial de carga, ésta es debida al exceso o defecto de electrones en cada una de las terminales, esta diferencia de carga establece una diferencia de potencial, el voltaje es el trabajo que se debe realizar para mover ésta carga. Se dice que es un voltaje directo o DC, pues es una línea recta que se puede obtener o visualizar en el osciloscopio. La gráfica que representa el voltaje DC, es una línea recta constante y continua en el tiempo, para al eje horizontal, es un voltaje constante, luego el uso de éste tipo de energía es relativamente óptimo en los sistemas electrónicos pues ofrece de manera constante potencia y energía al sistema.
Figura 1.7.2.1 Voltaje DC

21. Trabajo colaborativo:
Actividad 1.7.1.:
Descargue del link:
http://assets.fluke.com/manuals/175_____umspa0100.pdf el documento respectivo, lea y analice las características del multímetro. Familiarícese con su aspecto y funcionamiento, reúnase con sus compañeros y responda:
A. ¿Qué variables pueden medirse con éste instrumento?
B. ¿Qué rangos de voltaje mide en AC?
C. ¿Qué rangos de Corriente en AC se pueden medir con el instrumento?
D. ¿Cuál es el valor máximo de resistencia que se puede medir con él?
E. Observe la tabla que se encuentra en la página 2 de dicho manual y realice una comparación entre los íconos para las variables de corriente y voltaje tanto alternos (AC) como directos o continuos (DC o CC).
RESUMEN
Desde el momento en que el hombre empezó a utilizar adecuadamente la energía eléctrica fue implementando una serie de elementos que le permitieron aplicar no solo conceptos físicos sino desarrollar aparatos

22. tecnológicos; estos aparatos tecnológicos, han venido facilitando la vida del hombre, desarrollando nuevas áreas del conocimiento, como la electrónica.
Desde el punto de vista físico, la energía eléctrica se desprende de la energía que se puede aprovechar desde el electrón, el cual al pasar de un nivel a otro de energía, permite obtener dicho tipo de energía.
El flujo de electrones o corriente, permite el transporte de dicha energía, y el potencial, que es el trabajo necesario para el movimiento de dichos electrones se conoce como Voltaje. Este tipo de energía puede ser de dos formas según como sea generado, si se obtiene mediante movimiento mecánico se dice que es Alterno y si es debido a una distribución de electrones, se dice que es Directo o Continuo, existiendo entonces Corriente Alterna (AC) y Voltaje Alterno, que es el que llega a nuestras casas para ser usado en los diferentes electrodomésticos; por otro lado está el Voltaje y la Corriente Directa o continua (DC o CC), que es el que se obtiene en dos terminales de diferente naturaleza donde se encuentra una mayor o menor cantidad de electrones, en la terminal con exceso de electrones, se le asigna el polo negativo (-) y al terminal con defecto de electrones se le asigna el polo positivo (+), se debe tener cuidado de no confundir el polo positivo con los protones que tienen carga positiva en el electrón, éste nada tiene que ver con el polo positivo, pues es la cantidad de electrones la que da la polaridad en las terminales por ejemplo de una batería o pila.
Las principales características a tener en cuenta en el análisis de una señal alterna (AC) son: Frecuencia (f), Amplitud (A), Periodo (T) y Fase (θ). La frecuencia son los ciclos de la señal por segundo, es decir cuántas “vueltas” en 1 segundo tiene dicha señal y su unidad de medida es el Hertzio (Hz); la amplitud es que tan “grande” es la señal y se determina por los niveles máximos y mínimos, su unidad depende de si la señal es de corriente o de Voltaje, en cuyo caso será en amperios o voltios respectivamente.
BIBLIOGRAFIA RECOMENDADA

23. INTERNET
http://fresno.pntic.mec.es/~fagl0000/clasificacion.htm
http://www.unicrom.com/TuT_codigocolores.asp
http://books.google.com.co/books?id=LdzhG3XZd2IC&pg=PA73&dq=CLASIFCACION+DE+LAS+RESISTENCIAS#PPA72,M1
http://www.yoreparo.com/foros/electronica/soluciones/codigos-y-simbolos-en- electronica-con-videos-t186616.html
TEXTOS:
ROBBINS, Allan. Análisis de circuitos Teoría y práctica. Introducción. Cengace Learning. 2007. p. 3 - 21.
NEXO
Los conceptos de Energía, Voltaje y Corriente, son fundamentales para el resto del curso, pues de ellos depende en buena medida el análisis hecho a los circuitos, al igual que el concepto de resistencia, la notación científica es utilizada en todos los contextos sobre todo el uso de los prefijos para múltiplos y submúltiplos de las diferentes variables, esta facilita la expresión y tratamiento de las diferentes magnitudes y medidas.
SEGUIMIENTO DE AUTOAPRENDIZAJE
A continuación se encuentra una serie de preguntas que le orientarán en el repaso de los temas a manera de evaluación, resuelva cada uno de ellos procurando citar lo menos posible la bibliografía y los conceptos de que se evalúan en éste documento.
1. En un experimento realizado se encontró que la energía requerida para mover un mecanismo era de 120 Julios, si 1 eV es 1,602 x 10-19 Julios,

24. exprese la conversión de Julios en electronvoltios (eV), usando la notación científica mediante exponentes y prefijos en la escala adecuada.
2. En la siguiente tabla se encuentra el radio de algunos planetas del sistema solar, exprese cada uno de ellos en el múltiplo más cercano correspondiente:
Planeta
Radio en metros2
Radio en Mega metros
Tierra
6,38 x 106
Júpiter
7,18 x 107
Saturno
6,03 x 107
Urano
2,67 x 107
Marte
3,43 x 106
3. En la siguiente grafica identifique: Amplitud, frecuencia, periodo, en el punto señalado.
2 SEARS, W. Francis y Equipo; Física Universitaria Sexta Edición. Ed. Addison –Wesley.1988. Página 1079.
050100150200250300350-1-0.8-0.6-0.4-0.200.20.40.60.81X: 318Y: 0.682Grados Voltios Grafico de Voltaje Vs Angulo

25. 4. Realice una breve explicación sobre, la forma como se produce energía en una termoeléctrica, según el gráfico de la Figura 1.3.1

26. MODULO 2
2. RESISTENCIAS
INTRODUCCIÓN
Un concepto importante que todo estudiante del curso de electrónica básica debe tener claro es el de resistencia, a él se asocian muchos de los conceptos y funcionamiento de los diferentes diseños y aplicaciones en electrónica; por ejemplo, en los sistemas de audio, muchas veces se observa que un parlante tiene una medida de 8 Ohmios, en los equipos de comunicaciones aparece en la ficha técnica una “impedancia” de 75 Ohmios. El significado de dichas magnitudes, como lo podrá comprobar más adelante, en la profundización de los conceptos, tiene unas implicaciones desde el punto de vista práctico sobre la electrónica bajo un soporte teórico fundamentado en la física de materiales.
Ladillo: Impedancia es el concepto en AC asociado al de resistencia, aunque se puede inferir que es muy similar éste difiere del de resistencia en que la resistencia es una propiedad intrínseca del material mientras que la impedancia es una propiedad dinámica que aparece como respuesta a un estímulo.
En éste capítulo solo usaremos el concepto de resistencia, pues en el caso de la impedancia, se hace necesario realizar un curso de circuitos eléctricos, bajo el análisis del comportamiento de dispositivos en AC, sin embargo dada la relación entre mencionados conceptos, vale aclarar que es necesario su estudio y comprensión parta luego realizar la profundidad de éste según se considere, en los cursos futuros.
La deducción y aplicación de la ley de Ohm, permite tener una idea global del funcionamiento de los dispositivos y diseños electrónicos; a partir de ésta y sin mucho esfuerzo, se puede inferir un diagnóstico preliminar, detectando rápidamente posibles fallas, por ello es de gran importancia dicho concepto,

27. pues mencionada ley relaciona tanto esta propiedad como el de la corriente y el voltaje.
Se sugiere desarrollar cada actividad y ejercicio disciplinadamente, teniendo en cuenta la aplicación de los conceptos y la claridad sobre ellos en cada momento del capítulo, realizando las preguntas pertinentes y las consultas adicionales que se generen a partir del estudio de éste material.
MAPA CONCEPTUAL:
LOGROS:
 Identifica la propiedad de la resistividad en los materiales como característica fundamental en la conducción eléctrica y la asocia al fenómeno de la resistencia eléctrica.
 Diferencia la propiedad de la resistividad de materiales con el de resistencia eléctrica
POTENCIA
RESISTENCIA
CORRIENTE
VOLTAJE
LEY
DE OHM
MULTIMETRO
NOMENCLATURA
MEDICION
RESISTIVIDAD
RESISTENCIA
ELECTRICA
MIXTO
PARALELO
SERIE
CIRCUITOS
CONDUCTIVIDAD

28. 2.1 RESISTIVIDAD
“… la resistencia eléctrica que presenta un material a una corriente multiplicada por la sección transversal del flujo de corriente y por la unidad de longitud del camino de la corriente”3, es la definición de resistividad, que es el inverso de la conductividad, la resistencia es una propiedad de todo material y se relaciona con la resistividad como propiedad única de dicho material, relacionada tanto con la longitud como con el área de la sección transversal, de aquí se infiere la diferencia entre resistencia y resistividad, al observar la fórmula, se aprecia dicha conclusión, en la siguiente tabla se muestra algunas resistividades de materiales usados comúnmente:
Tabla 2.1.1 Resistividad de algunos materiales
Material
Resistividad (ρ) Ω-cm
Plata
1,5 x 10-6
Cobre
1,7 x 10-6
Carbono (Grafito)
2,6 x 10-6 a 190 x 10-6
Nicromo
100 x 10-6
Vidrio
1010 x 1014
SEIDMAN, H. Artur. Electrónica Práctica y Moderna. Tomo 1. McGraw Hill. 1995. p.1-3.
2.2. RESISTENCIA
Hay una gran variedad de resistencias que se pueden encontrar en lo cotidiano; desde el concepto natural la resistencia es una oposición, en éste caso se habla de la resistencia como elemento en electrónica, desde éste punto de vista, se puede definir la resistencia eléctrica como: la oposición que
3 PARKER, P. Sybil Electrónica práctica y moderna, Tomo 4, pag.282. Ed. Mc Graw Hill.

29. se presenta en un material al movimiento de cargas o flujo de electrones, la unidad de medida de la resistencia es el Ohmio y se representa por la letra griega Omega Ω. Los valores comunes de resistencias son del orden de los Kilo ohmios, aunque encontramos resistencias en unidades, decenas y centenas de Ohmio, es decir al remitirnos a la tabla 1.5.1, se usan los múltiplos.
Hay muchas clases de resistencias eléctricas, pero se pueden clasificar en 2: Resistencias fijas y resistencias variables. Las resistencias fijas, como su nombre lo indica, son aquellas que tienen un valor fijo, es decir, el fabricante garantiza un valor único que se da según un nivel de tolerancia; por otro lado las resistencias variables, son aquellas que varían en un rango de valores, desde 0 ohmios, hasta el valor para el cual fueron diseñadas.
Los símbolos para las resistencias variables y fijas son:
Figura 2.2.1 Símbolo de las resistencias fijas (arriba) y variables (abajo)
Existen muchos, sensores que aprovechan el efecto resistivo, es decir, varían la resistencia como propiedad de los materiales ante un fenómeno físico, como temperatura, humedad, presión etc. A estos sensores se les conoce como sensores resistivos.
La resistencia de cualquier material está dada por:
Ecuación de la Resistencia 2.2.1
R410k 40% R3RESISTORR210k 40% R11k

30. Donde:
R= Resistencia
ρ = Resistividad del material, Ohmio por centímetro (Ω-cm)
L = Longitud del material cm
A = Área de la sección transversal del materia. cm2
Ladillo: La sección transversal hace referencia a un corte imaginario que se hace del material, por ejemplo, si el material tiene forma cilíndrica, la sección transversal es una circunferencia, como se muestra en la figura L1, por eso la unidad es el centímetro cuadrado: cm2 recordar que para dicho caso, la sección transversal, el área de la circunferencia esta dad por: A =πxr2
Figura L1. Sección transversal de un material cilíndrico
2.2.1. LEY DE OHM
La relación entre voltaje, corriente y resistencia fue formulada por George Simon Ohm, conocida como la Ley de Ohm, la cual se define como:
“La corriente que circula en un circuito es directamente proporcional al voltaje e inversamente proporcional a la resistencia”4
4 GUTIERREZ, Ramírez Humberto, Electrónica Análoga, Vol. 1; 8ª Edición, Pag. 1

31. La fórmula que resume dicho principio esta dado como:
Ecuación 2.2.1.1
Desde mencionada formula, se deducen muchas de las propiedades y análisis de los circuitos que se tratan en éste documento, se sugiere tener muy presente mencionada ecuación.
Un concepto adicional que aparece, es el de potencia, en éste caso, la potencia en las resistencias, está dada como la relación que existe entre la energía consumida y la disipada, es decir, el intercambio de energía y se define como sigue: “La potencia en una resistencia es directamente proporcional al cuadrado de la corriente por una constante de proporcionalidad que es la resistencia”, la fórmula que resume dicho enunciado es:
Ecuación 2.2.1.2
Si usamos la ley de Ohm y despejamos la corriente se tiene que la Ecuación 2.2.1.2, queda:
Ecuación 2.2.1.3
En resumen, para la potencia se puede usar una de las tres fórmulas que se presentaron anteriormente. La unidad de medida es el Vatio (Watts), que se usará en éste texto, aunque existen otras unidades de medida.
2.3. RESISTENCIA ELÉCTRICA
Como se mencionó en la parte introductoria, sobre las resistencias, se define como la propiedad que relaciona la resistividad con la longitud del material y la sección transversal de éste.
La ecuación 2.1 define el concepto de resistencia eléctrica, la unidad de medida de la resistencia es el Ohmio, usando la tabla 1.5.1, se debe tener presente el uso de los múltiplos, los cuales facilitan la expresión de dichas

32. cantidades, pues los valores usados en electrónica, son grandes, dadas las magnitudes de corriente.
El aspecto de muchas resistencias difiere según el fabricante y la aplicación, el aspecto de la resistencia de una ducha para agua caliente difiere de la que se observa en los circuitos convencionales electrónicos, lo mismo sucede si se tiene como referente las resistencias de potencia, las cuales tiene forma de prisma rectangular. En la siguiente figura, se observan algunas resistencias para familiarizase con su aspecto físico:
Figura 2.3.1 (A) Resistencia eléctrica a partir de una cinta aislante y un alambre bobinado; (B) Resistencia para montaje superficial (SMD); (C) Fotorresistencia; (D) Resistencia eléctrica para calentador; (E) Varias clases de resistencias (A. Resistencia de carbón ½ W. B. Resistencia de Film de carbón NOS ½ W. C. Resistencia de Film de Carbón NOS 1W. D. Resistencia de Oxido de metal de 2 W. E. Resistencia de alambre de 5 W5)
A B C D E
A.http://patentados.com/invento/resistencia-electrica.html B.http://upload.wikimedia.org/wikipedia/commons/7/76/Register3.jpg. C.http://upload.wikimedia.org/wikipedia/commons/a/a2/Fotocelda.jpg D.http://www.paginasamarillas.com.pe/dbimages/988195/988195_104660_ZOOM_PRODUCTO.JPG
5 Tomado de http://www.retrogames.cl/pasivos.html,

33. E. http://www.retrogames.cl/imagenes/clases/resistors.jpg
Un concepto importante que se tratara en la sección correspondiente, es el de potencia, sin embargo, en la figura 2.3.1. (E), se puede observar la relación del tamaño de la resistencia con la potencia, si se profundiza en el material utilizado, se notará tal relación. La potencia está relacionada con la energía potencial, la cual debe ser disipada como consecuencia de la oposición de la resistencia a la corriente, según el principio de conservación de la energía, estudiado en la sección 1.1, ni se crea ni se destruye, solo se transforma, por ende, la energía dada la oposición del material al flujo de electrones, se traduce en calor.
Existe una gran variedad de las resistencias variables, conocidas como potenciómetros o trimmers, en la siguiente figura, se observan algunos dibujos de ellos.
Figura 2.3.2. Algunas clases de potenciómetros
Tomado de: http://www.gmelectronica.com.ar/gm/graficos/catalogo/127.JPG [Cit. 23 Dic., de 2009]
APRENDIZAJE COLABORATIVO:

34. Actividad:
Realice los siguientes ejercicios de manera individual, acto seguido reúnase con sus compañeros de curso, comparta sus inquietudes y posibles soluciones.
 Hallar la resistencia de una varilla de cobre de 2 m de longitud y 8 mm de diámetro, sabiendo que la resistividad de este metal vale 1,756x10-8 Ω m.
 Hallar la resistencia de un alambre de plata alemana de 152,5 m de longitud y 0,3 mm2 de sección. La resistividad de este metal es 33x10-6 Ω cm.
 Un hilo de cobre tiene un diámetro de 4 mm. Hallar la resistencia de 300 m de dicho conductor a 20º C, sabiendo que la resistividad del cobre a esta temperatura es de 1,8x10-8 Ω m.
Un concepto asociado al de resistencia es el de Impedancia, ésta aparece al hacer el análisis de circuitos en AC, donde la señal se puede representar como un vector, el efecto que causa cada elemento sobre dicha señal se representa en un plano cartesiano donde hay una componente Real y una componente Imaginaria, la componente real en un circuito AC, es la impedancia que es el equivalente a la resistencia, su medida se da en Ohmios. Este tema se trata con profundidad en un curso especial de análisis de circuitos en AC, con elementos de análisis llamados fasores o análisis fasoriales.
Ladillo: Un numero imaginario es aquel que se deduce de la raíz negativa de un número, para evitar éste tipo de indeterminaciones, se reemplaza por la letra de tal forma que un numero como es 5 , también es muy común encontrar expresiones como 2 + 3 , la parte real de dicho numero es 2 y la parte imaginaria es 3.

35. Como se explicó en la sección 1.4 la conductancia es el inverso de la resistencia y la resistencia es el inverso de la conductancia, de tal forma que:
Ecuación 2.3.1
La unidad de medida para la conductancia es el siemens, que es el inverso del Ohmio y viceversa.
2.3.1. DEFINICIONES Y SÍMBOLO
Aunque existe un sinnúmero de formas para representar una resistencia, en los planos o circuitos se encuentran generalmente tal como se observa en la figura 2.1 a cada resistencia, se asocia la letra R y un número que corresponde al orden, adicional se escribe el valor de ésta frente a cada una de ellas, en muchas ocasiones, se ubica en la parte inferior para evitar confusiones en el plano. En la Figura 2.3.1.1, se observa un circuito de resistencias usando el software Circuit Maker, éste facilita el diseño e implementación de circuitos, como se explica en la sección correspondiente.
Figura 2.3.1.1. Circuito resistivo usando Circuit Maker
Se observan 2 elementos que son una fuente de energía, en éste caso de voltaje Vs1 de 10 V (Voltios) y un punto de referencia llamado tierra (GND),
+ - Vs110VR31kR21kR11k

36. representado por líneas paralelas de tamaño descendente, en la parte inferior izquierda del circuito.
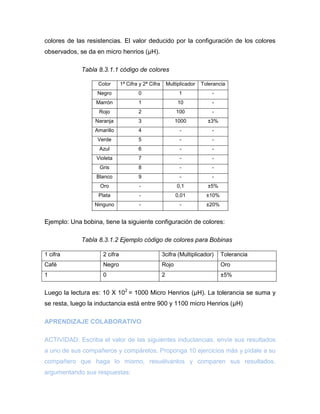
2.4. CÓDIGO DE COLORES
Para determinar el valor de una resistencia, se debe tener en cuenta un código internacional, llamado código de colores, éste no solo se usa en las resistencias, también se usa en otros componentes, para determinar a simple vista el valor de dicho componente, aunque no es un método exacto, su valor aproximado debido a la tolerancia, o margen de error es muy aceptable en el momento de realizar diseños de circuitos.
En la Figura 2.3.1, se observan algunas resistencias, note que cada una de ellas tiene unas bandas de colores, dichas bandas se interpretan según el código de colores como se explica a continuación y de esta manera se determina su valor.
En la Figura 2.4.1 se observa una resistencia con sus respectivas bandas de colores, el orden de dichas bandas, debe tenerse en cuenta para determinar el valor de ésta.
Figura 2.4.1 Orden en las bandas de colores en una resistencia.
Tomado de: http://es.wikipedia.org/wiki/Archivo:Resistencia.svg [Citado 20 de Dic,. 2009]
Las bandas se deben leer ubicando la banda de tolerancia a la derecha, para detectar la banda de tolerancia, basta con observar la que está más apartada, ésta se ubica muy cerca a uno de los bordes.

37. En la Figura 2.4.2 se observa el orden y el valor de cada uno de los colores. Las 3 primeras bandas se interpretan como cifras, la cuarta banda es el valor de la tolerancia, dicho valor debe sumarse o restarse al valor nominal de la resistencia, es decir el dado por el código de colores; en muchas ocasiones se pueden encontrar resistencias hasta con 5 bandas, en cuyo caso las 4 primeras bandas son el valor nominal y la quinta es la tolerancia, se debe prestar atención a ésta cifra, pues como se muestra en el ejemplo, determina el valor verdadero de la resistencia, sin embargo una mejor medición puede obtenerse con el multímetro, como se explicará en dicha sección.
Figura 2.4.2 Código de colores
Tomado de: http://www.unicrom.com/TuT_codigocolores.asp [cit. 22 Dic., 2009]
A continuación, se explica el uso de la tabla, en la determinación del valor de una resistencia, de 4 bandas y de 5 bandas, las resistencias de 5 bandas, se conocen con el nombre de resistencias de precisión.

38. Ejemplo 2.4.1: las bandas de colores para una resistencia con 4 bandas de colores son:
1ª Banda: Café
2ª Banda: Negro
3ª Banda: Rojo
4ª Banda: Plateado
Como se observa en la tabla los valores para cada banda son:
1ª Banda: 1
2ª Banda: 0
3ª Banda: 2
4ª Banda: ±10%
Con dichos números se procede como se indica a continuación:
El primer número o cifra corresponde a 1, el segundo a 0 y el tercero o multiplicador es el número o potencia de 10 con el cual se debe multiplicar, en éste caso el 2 indica el exponente de la base que es 10 es decir 102 = 100, luego aritméticamente se realiza la siguiente operación:
10 x 100 = 1000 Ω
La tolerancia del 10 % se debe sumar y restar a éste valor, a 1000 se le halla el 10% y nos da 100, luego le resto y le sumo 100 a 1000, como se muestra a continuación:
1000 - 100 = 900 Ω que se puede representar como 0.9 KΩ
1000 + 100 = 1100 Ω que se puede representar como 1.1 KΩ

39. Luego el valor de la resistencia está entre 900 y 1100 Ohmios, por ejemplo 980, 1050 Ohmios etc. La forma más exacta, si se usa adecuadamente, es mediante el multímetro, el cual se explicará más adelante, en la sección 2.6.3.
Para las resistencias de 5 bandas, se debe tener en cuenta que son 3 bandas para cifras significativas, una banda para la cifra multiplicadora y una banda para la tolerancia.
Ejemplo: En la siguiente tabla se muestra un ejemplo de una resistencia de precisión con 5 bandas de color:
1ª Cifra
2ª Cifra
3ª Cifra
4ª Cifra Potencia
Tolerancia
Café
Negro
Rojo
Rojo
Rojo
1
0
2
2
2
Para interpretar dicho valor se tiene que:
102 x 102 = 102 x 100 = 10200 Ohmios (10,2 KΩ)
La tolerancia de 2% significa, que debemos hallar el 2% del valor hallado (204 Ω Ohmios) para sumarlo y restarlo a dicho valor como se indica a continuación:
10200 + 204 = 10404 Ω
10200 – 204 = 9996 Ω
Si aplicamos la notación científica, corremos la coma desde la última cifra hacia la izquierda 3 espacios y la expresamos en Kilo Ohmios (KΩ); es decir: 10,404 KΩ y 9,996 KΩ.
RESUMEN

40. En el capítulo estudiado, se conceptualizó sobre la propiedad intrínseca de los materiales, llamada Resistencia, ésta se asocial al concepto de resistividad por la ecuación: 2.2.1. De igual forma, las variables de voltaje y corriente se relacionan con éste a partir de la Ley de Ohm, mediante la ecuación 2.2.1.1. El código de colores, (Tabla 2.4.1) permite identificar de primera mano el valor de una Resistencia, este obedece a un orden establecido desde la tabla y el cual se explica con el ejemplo 2.4.1. cabe anotar que este valor es relativo, pues existe una tolerancia, interpretada a partir del código de colores y la cuarta banda o quinta, según sea el caso de una resistencia de precisión o no.
BIBLIOGRAFIA RECOMENDADA
INTERNET:
http://fresno.pntic.mec.es/~fagl0000/clasificacion.htm
http://www.yoreparo.com/foros/electronica/soluciones/codigos-y-simbolos-en- electronica-con-videos-t186616.html
TEXTO:
ROBBINS, Allan. Análisis de circuitos Teoría y práctica. Cap.3. Cengace Learning. p. 51
NILSSON, James. Circuitos Eléctricos. Cap. 3. Pearson Prentice Hall. p. 66
NEXO
El concepto de resistencia se relaciona con el siguiente capítulo donde se estudia el caso de las resistencias en serie y en paralelo. Dada una topología es indispensable que se verifique o compruebe los resultados a partir de las ecuaciones planteadas y los cálculos mediante la ley de Ohm. La resistencia equivalente y mediciones hechas, dan cuenta no solo de los componentes que conforman cada arreglo, sino de los resultados obtenidos expresados en la

41. notación y unidades adecuadas, de ahí la importancia en la comprensión del concepto de resistencia.
SEGUIMIENTO AL AUTOAPRENDIZAJE
A continuación en la tabla, se presentan valores para resistencias de precisión, escriba en la casilla correspondiente, los valores de resistencias teniendo en cuenta la tolerancia.
1ª Cifra
2ª Cifra
3ª Cifra
4ª Cifra
Tolerancia
Valor
Café
Negro
Naranja
Rojo
Café
Café
Negro
Negro
Rojo
Rojo
Amarillo
Violeta
Negro
Gris
Naranja
Verde
Azul
Negro
Rojo
Rojo
Azul
Verde
Café
Café
Café
Determinar el valor de cada resistencia, teniendo en cuenta los valores de tolerancia en cada caso.
1ª Cifra
2ª Cifra
3ª Cifra
Tolerancia
Valor
Amarillo
Negro
Verde
Dorado
Café
Rojo
Violeta
Dorado
Rojo
Rojo
Rojo
Plateado
Verde
Violeta
Negro
Plateado
Café
Negro
Verde
Dorado

42. MODULO 3
3. ASOCIACIÓN DE RESISTENCIAS
INTRODUCCION
El análisis de las aplicaciones en electrónica requieren tener una visión global del sistema, la resistencia es una propiedad intrínseca de los materiales, presente en cualquier situación donde existen componentes electrónicos, sin embargo, las resistencias pueden estar asociadas de diferentes maneras y la simplificación de éstas, permite tener una apreciación de su funcionamiento en una primera instancia, para luego realizar los análisis que dicha situación requiera.
En éste capítulo se estudia la forma como se simplifican las resistencias en sus diferentes configuraciones, serie, paralelo y mixto, de ésta manera, el análisis donde intervienen dispositivos con características resistivas se hace más fácil y efectivo.
Se hace necesario que se tomen los temas con la mayor disciplina posible, teniendo siempre `presente que el concepto quede claro, de no ser así los temas siguientes serán de mayor dificultad comprensiva.
MAPA CONCEPTUAL

43. LOGROS
 Analiza circuitos resistivos, en serie, paralelo y mixto, según los modelos planteados.
 Determina las variables eléctricas de voltaje, corriente y potencia sobre cada una de las resistencias en un circuito dado.
CONFIGURACIONES
En ésta sección, se explica el concepto inicial de circuito y el de resistencia equivalente, aunque en muchas ocasiones los circuitos que se presentan no se encuentran en lo cotidiano, como ejercicio didáctico es necesario e interesante su análisis y desarrollo.
Resitencia Eléctrica
Circuitos resistivos
Serie
Paralelo
Mixto
Análisis
Ley de Ohm
Mallas
Nodos
Potencia

44. La configuración básica de los circuitos resistivos puede ser en serie, paralelo
o mixto, para explicar cada uno de ellos, se parte del concepto y se representa
el circuito usando el software de simulación Circuit Maker.
a) Circuito Serie: Las resistencias en serie, se conectan una
seguida de la otra por un único terminal, observe en la Figura
2.4.1 que dicho componente solo tiene 2 terminales.
Figura: 3.1 Resistencias en serie
b) Circuito Paralelo: Las resistencias en paralelo, se conectan por
2 terminales, en la Figura se muestra como se conectan, aunque
se debe observar que estén conectados por los 2 terminales.
Figura. 3.2 Resistencias en paralelo
c) Circuito Mixto: Un circuito mixto, tiene tanto resistencias en
configuración serie, como paralelo, como se indica en el circuito:
Figura. 3.3 Circuito mixto de resistencias
R1 R2 R3 Rn
R1 R2 R3 Rn

45. 3.2 CÁLCULOS EN CIRCUITOS RESISTIVOS
Para hallar la resistencia equivalente, en cada uno de los casos, se procede de manera diferente, según como sea, serie, paralelo o mixto, a continuación, se explica en cada uno de ellos cómo se debe hacer.
3.2.1. CIRCUITO SERIE:
La resistencia equivalente para las resistencias en serie, debido a que el efecto resistivo es sumado, es decir la oposición total de las resistencias conectadas en serie es sumado, pues su efecto al oponerse a la corriente es el mismo, sin importar el valor de la resistencia su efecto es igual, sin embargo, cada una con su valor resistivo se suma a otro. En resumen, las resistencias en serie se suman. EL efecto sobre el voltaje es diferente, el voltaje disminuye a medida que pasa por cada resistencia.
Para hallar la resistencia equivalente se suma el valor de cada resistencia, luego la ecuación para las resistencias en serie de la Figura 3.1 es:
Ecuación 3.1.1
Un ejemplo de circuito serie, puede ser como el observado en la Figura 3.1.1.1, dando valores a cada resistencia como se muestra a continuación, se puede determinar la resistencia equivalente:
Figura 3.2.1.1 ejemplo de resistencia en serie
+V110VRnR3R2R1

46. Como se puede ver cada resistencia tiene su propio valor, y tiene asignado un
nombre. Para hallar la resistencia equivalente se suman los valores de las
resistencias.
Luego el valor de la resistencia equivalente Req es de 162,5 KΩ (Ciento sesenta y
dos coma cinco Kilo Ohmios)
APRENDIZAJE COLABORATIVO:
Actividad:
Realice el cálculo para las siguientes resistencias en serie, envíe sus respuestas a
sus compañeros y compare los resultados, argumente sus respuestas donde sea
necesario.
a.
b.
c.
d. ¿Qué valor debe tener R4, si la Req
es de 1.68 KΩ (Kilo Ohmios)?
e. ¿Qué valor debe tener R4, si la Req
es de 19/18 MΩ (Mega Ohmios)?
Req
R4
150k
R3
10k
R2
1,5k
R1
1k
R4
150M
R3
0.5M
R2
1,5M
R1
1M
R4
2,4k
R3
1,5k
R2
1000
R1
500
R4
5/2K
R3
2/8K
R2
3/4K
R1
1/2K
R3 R4
1/3K
R2
3/4K
R1
3/5K
R3 R4
2/9M
R2
3/6M
R1
1/3M

47. 3.2.1.2. OTROS CÁLCULOS EN CIRCUITOS RESISTIVOS SERIE
Las variables a analizar en los circuitos resistivos son el voltaje, la corriente y la potencia, teniendo en cuenta la ley de Ohm y algunos principios básicos fundamentales, se pueden deducir fácilmente dichas variables en cada una de las resistencias.
A continuación, se explica cómo deducir dichas variables tomando como base el circuito de la Figura3.1.1.1, se implementa una fuente de voltaje DC, la cual puede ser una batería o una de las fuentes de laboratorio, en la Figura 3.1.1.2.1 del siguiente ejemplo, se muestra uno de los símbolos eléctricos para éste tipo de dispositivos, usado en los planos o diagramas esquemáticos.
Ejemplo: Se propone analizar el siguiente circuito, determinando las variables de Voltaje (V), corriente (I) y Potencia (W)
Figura 3.1.1.2.1 Circuito resistivo con fuente de voltaje
Note los dos símbolos que aparecen, la fuente de voltaje de 10 Voltios (V1=10V) y el símbolo de tierra o referencia que se encuentra en la parte inferior.
Para realizar el análisis de este circuito se debe partir de algunos principios como son:
 Un circuito es una serie de elementos que se interconectan mediante un alambre conductor, formando un sistema con una o varias entradas y una o varias salidas.
R11kΩR21.5kΩR310kΩR4150kΩV110 V

48.  A través de una trayectoria cerrada o circuito fluye una corriente, la corriente total es la corriente que debe suministrar la fuente a todos los componentes del circuito.
 Las resistencias se oponen al flujo de corriente, luego en ellas debe “verse” reflejado un trabajo o potencial, es decir la resistencia provoca un cambio o caída de voltaje y consume una potencia.
 En cada resistencia se debe aplicar la ley de Ohm V = IXR.
 La corriente en un circuito serie es la misma pero el voltaje es diferente, en cada resistencia, esto se puede deducir fácilmente, si reemplazamos las cuatro resistencias por una sola, la corriente que la fuente debe suministrar es la misma, pues el efecto de oposición se suma.
Con estas premisas, se inicia el análisis, lo primero que debemos hacer es determinar la corriente que pasa por las resistencias, que es igual para cada una, para ello, reemplazamos todas las resistencias por una sola, es decir por la Req, se aplica la ley de Ohm, tomando el voltaje de la fuente como se indica a continuación:
Tomando el valor de la resistencia y el de la fuente de voltaje, se halla la corriente a partir de la ley de Ohm:
Req162.5kΩV210 V

49. Con dicha corriente se puede hallar los voltajes sobre cada resistencia, pues dicha corriente es igual para todas las resistencias en serie, aplicando ley de Ohm nuevamente, se tiene que:
Para comprobar si las respuestas son correctas, se suman los voltajes y dicha suma debe ser igual al voltaje de la fuente, como se indica a continuación:
El valor obtenido es muy cercano a los 10V al redondear dicho valor.
Los valores de potencia, se obtienen teniendo en cuenta la corriente y el voltaje sobre cada resistencia o cualquier variable que relacione la ecuación de potencia de la Ecuación 3.2.2 y 3.2.3. Se tiene que para este caso se usa la siguiente ecuación de potencia: P = V x I, los cálculos se muestra a continuación:
Por el mismo principio de conservación de la energía, se suman las potencias y ésta sumatoria debe ser igual a la potencia total del sistema, como aparece a continuación:

50. Como se puede observar que los valores son muy similares por tanto se hace la validación de dichos resultados.
3.2.2 CIRCUITO PARALELO:
Las resistencias en paralelo, se pueden reemplazar por una sola resistencia equivalente, el efecto que causan sobre la corriente se conoce como divisor de corriente, para explicarlo se debe tener en cuenta la ley de nodos de Kirchhoff, esta se puede explicar de la siguiente manera: al llegar una corriente a un nodo, esta se divide, como si fuese una tubería por donde circula agua, la tubería principal distribuye el agua a las demás tuberías más pequeñas, luego la corriente se divide, pero el voltaje permanece constante. La resistencia equivalente inversa, es igual al inverso de cada una de las resistencias en paralelo, lo cual se puede expresar de la siguiente manera:
Ecuación 3.1.2.1 Resistencias en paralelo
Se debe tener especial cuidado con ésta ecuación, pues como se puede notar, al finalizar el cálculo no se halla la Req sino su inverso, por tanto se debe invertir el numerador y el denominador del resultado final; para mayor claridad, se realizará un cálculo sencillo para familiarizarnos con dicha ecuación.
Ladillo: Un nodo es un punto de un circuito donde se unen dos o más hilos conductores.
Un ejemplo se expone a continuación: Se quiere hallar la resistencia equivalente para un circuito paralelo como el que se muestra en la Figura 3.1.2.1
Figura 3.1.2.1 Resistencias en paralelo
ReqR4200KR32/9MR23/6MR11/3M

51. Se halla la resistencia equivalente, según la Ecuación 2.4.2 de la siguiente manera:
Note que todos los valores se dan en MΩ, por ello 200KΩ se expresa como 0,2 MΩ. Una forma para resolver esta suma de fraccionarios puede ser:
Ahora, observe que el valor hallado debe invertirse, pues se obtuvo el inverso de la resistencia equivalente: por tanto se debe invertir el resultado de la siguiente manera:
Debe tenerse especial cuidado con las unidades, note que todo el desarrollo del ejercicio se tuvo en cuenta que las resistencias estaban expresadas en KΩ. Se debe estar muy familiarizado con el desarrollo de operaciones con números fraccionarios, esto facilitará su desempeño en el tema.
Continuando con el análisis tal como se hizo en el circuito serie, se plantea el ejercicio de usar una fuente de voltaje, para determinar la corriente, el voltaje y la potencia, en cada una de las resistencias, como se muestra en el siguiente ejemplo:

52. Ejemplo: Analizar el circuito de la Figura 3.1.2.1, hallando los valores sobre cada
resistencia de: Voltaje (V), corriente (I) y potencia (W).
Figura 3.1.2.1 Circuito Paralelo a analizar
Inicialmente se parte de las siguientes consideraciones:
 Las resistencias están conectadas entre si por dos terminales, luego están
en paralelo.
 Si se mide el voltaje entre el punto de referencia, o tierra (GND), que se
encuentra en la parte inferior de la fuente de Voltaje, representado por
varias líneas paralelas que decrecen en su tamaño, y la parte superior del
circuito, esto entre los dos extremos superior e inferior, el valor obtenido es
siempre el mismo, pues solo hay un alambre conductor, no hay ningún
elemento entre ellos. “El voltaje en un circuito paralelo es igual”
 Como el alambre que conecta las resistencias por la parte superior es igual,
se dice que es un solo “nodo”. Si se analiza desde el punto de vista de la
corriente, nótese que de la fuente sale un flujo de electrones que se
distribuye por todas las ramas, para ilustrarlo, observe la Figura 3.1.2.2.
Figura 3.1.2.2. Corriente en un circuito paralelo.
+ V1
10V
R4
200k
R3
2/9M
R2
3/6M
R1
1/3M

53. Respecto a esta figura se debe observar que:
 Cada flecha, representa una corriente
 Las letras de la parte superior son los nodos o puntos de conexión, de dos o más “alambres”, conductores.
 Para cada nodo se tiene que:
o Nodo a: Entra la corriente I1 y salen las corrientes I2 e I3.
o Nodo b: Entra la corriente I3 y salen las corrientes I4 e I5
o Nodo c: Entra la corriente I5 y salen las corrientes I6 e I7
 Una de las leyes de Kirchoff, para la corriente dice que: “En un punto de conexión o nodo, la suma de las corrientes que entran, es igual a la suma de las corrientes que salen”. Luego expresando esto como una operación, para cada nodo, se tiene que:
o Nodo a: I1 = I2 + I3
o Nodo b: I3 = I4 + I5
o Nodo c: I5 = I6 + I7
Se puede notar que las corrientes tienen una estrecha relación, siendo el voltaje igual en cada resistencia, para éste ejemplo de 10 V, y teniendo los valores de las resistencias, al relacionar dichas variables, se puede inferir que se usa la ley de Ohm, expuesta en la sección 2.2. Para este circuito, con las anteriores consideraciones, se inicia el análisis de la siguiente manera:
 Planteamiento de ecuaciones: Las ecuaciones que rigen el circuito son:
o Nodo a: I1 = I2 + I3
o Nodo b: I3 = I4 + I5
o Nodo c: I5 = I6 + I7
o Cada corriente, según la ley de Ohm es:
o La resistencia equivalente, para el circuito está dada según la Ecuación 2.4.2.
 Análisis de relación entre las variables y determinación de valores.

54. o Si reemplazamos el equivalente, según la ley de Ohm en cada ecuación que hay para cada nodo, se tiene que:
o Nodo a: I1 = + I3
o Nodo b: I3 = + I5
o Nodo c: I5 = +
o La resistencia equivalente me permite determinar I1, pues esta corriente es la que “pide” todo el circuito, es decir es equivalente al total de corriente consumido por el circuito; éste procedimiento se desarrollo en la sección anterior, al circuito de la Figura 2.4.2, para este mismo circuito arrojando como resultado el siguiente:
Para ilustrar el proceso se redibuja el circuito con una sola resistencia, tal como se muestra en la Figura 3.1.2.3
Figura 3.1.2.3 Circuito resistencia equivalente paralelo
Aplicando Ley de Ohm a estos valores, se tiene que:
Luego las corrientes para el Nodo a, quedan:
Req68.93kΩV210 V

55. o Nodo a: 145,07μA = + I3, reemplazando los valores de V y R1, se tiene que: 145,07 μA = se despeja I3 y se obtiene:
o Nodo b: I3 = + I5, reemplazando el valor obtenido para I· del análisis anterior, se deduce :
o Nodo c: I5 = + en esta ecuación se puede comprobar que lo resultados obtenidos son verídicos, pues al deducir las corrientes sobre R3 y R4, deben ser iguales a la deducida para I5, así:
 Comprobación
3.2.3. CIRCUITO MIXTO:
En un circuito mixto hay una combinación de los dos efectos, se divide la corriente y el voltaje, para analizarlo, se debe seguir un procedimiento; aunque en muchos textos se presenta una fórmula que, aunque puede deducirse fácilmente, confunde pues se establece un parámetro de repetición que debe ser identificado con exactitud. En esta sección, se analizará un circuito mixto para deducir la formula de la resistencia equivalente.
El circuito planteado se encuentra en Figura 3.1.3.1
Figura 3.1.3.1 Circuito resistivo mixto

56. Inicialmente, debemos solucionar el problema de derecha a izquierda, de tal forma
que primero solucionamos las dos resistencias en paralelo, de éste queda solo
una resistencia como se muestra a continuación en los cálculos y el gráfico
respectivo.
Figura 3.1.3.2 Primer paso resolución de resistencias en paralelo
La ecuación que resume el paso anterior está dada por:
Al invertir la fracción para determinar la Req se tiene que:
Ahora se resuelve el circuito en serie de las tres resistencias en serie, se suman y
se obtiene una resistencia equivalente:
R1
20kΩ
R2
30kΩ
R3
50kΩ
R4
10kΩ
R1
20kΩ
R2
30kΩ
R3
8.33kΩ

57. La habilidad para resolver este tipo de ejercicios se obtiene únicamente
resolviendo ejercicios relacionados, en este ejemplo se propone, primero resolver
los paralelos y luego con la resultante, las resistencias en serie.
Aprendizaje colaborativo
Actividad 3.1.2.2
Halle la resistencia equivalente, el voltaje sobre cada resistencia y la corriente
respectiva, si se aplica una fuente de voltaje de 10 Voltios, en cada caso,
comparta sus respuestas con sus compañeros y argumente sus resultados.
A.
B.
C.
D.
R1
30kΩ
R2
30kΩ
R3
30kΩ
R4
R5 30kΩ
30kΩ
R1
20kΩ
R2
40kΩ
R3
20kΩ
R4
R5 30kΩ
10kΩ
R6
40kΩ
R7
1k
in1
in
R6
1k
R5
1k
R4
1k
R3
1k
R2
1k
R1
1k

58. E.
RESUMEN
El análisis de circuitos resistivos en las topologías serie, paralelo y mixto, permite
generar estrategias que simplifican el proceso de análisis. Las resistencias en
serie están regidas por la ecuación 3.1.1, mientras que las resistencias en paralelo
se dan mediante la ecuación 3.1.2.1. No se plantea una ecuación para el circuito
mixto, pues se hace necesario seguir el proceso de análisis para llegar a la
respuesta esperada.
Las leyes que permiten analizar las diferentes variables en los circuitos resistivos
como las de nodos y mallas, las ecuaciones 2.2.1.2 y 2.2.1.3 permite determinar
las variables de voltaje, corriente y potencia, permitiendo de esta manera no solo
corroborar en la práctica dichos análisis y realizar un proceso de diseño, sino
también corroborar el resultado de manera eficiente.
R3
100k
in1
in
R6
100k
R5
100k
R4
100k
R2
100k
R1
100k
R1
1kΩ
R2
1kΩ
R3
1kΩ
R4
1kΩ
R5
1kΩ
R6
1kΩ
R7
1kΩ
R8
1kΩ

59. BIBLIOGRAFIA RECOMENDADA
INTERNET:
http://www.yoreparo.com/foros/electronica/soluciones/codigos-y-simbolos-en- electronica-con-videos-t186616.html
http://fresno.pntic.mec.es/~fagl0000/clasificacion.htm
http://www.unicrom.com/TuT_codigocolores.asp
TEXTO:
ROBBINS, Allan. Análisis de circuitos Teoría y práctica. Cap.3. Cengace Learning. p. 53
NILSSON, James. Circuitos Eléctricos. Cap. 3. Pearson Prentice Hall. p. 63
NEXO
En el próximo capítulo, se estudiará una herramienta que permite corroborar los resultados obtenidos mediante las diferentes ecuaciones, dicha herramienta es el software de simulación. Aunque dicha herramienta facilita observar el comportamiento de un circuito en cualquier configuración, según los componentes utilizados, se hace necesario tener presente que los conceptos deben ser comprendidos y aplicados.
Se debe aplicar el concepto de potencia, corriente, voltaje y resistencia equivalente, para luego corroborarlo mediante el software de simulación, sin embargo el proceso de diseño permite que asumamos ciertos valores, esto no quiere decir que se apruebe el uso del método de ensayo y error sin ningún sentido, es necesario que se tenga claridad sobre los conceptos usados.
SEGUIMIENTO AL AUTOAPRENDIZAJE

60. 1. Se requiere que en el siguiente circuito, la corriente sea de: 44,77mA y la potencia de 447,76 mW. ¿Qué valor debe tener la resistencia y la fuente de voltaje faltante?
2. Realice el ejercicio 3-5 y 3-6 de la página 81 del texto sugerido en la Bibliografía anteriormente Recomendada. (ROBBINS, Allan. Análisis de circuitos Teoría y práctica)
3. Aplique la ley de Ohm a los ejercicios planteados en la sección 4-1 en las páginas 109 y 110 del texto sugerido en el numeral anterior.
4. Halle la resistencia equivalente de los ejercicios de la sección 5-3 Resistores en serie, en la página 142, del texto sugerido en el numeral dos.
5. Realice la identificación de conexión en serie y en paralelo de los ejercicios de la sección 6-1 en la página 174 que se encuentran en el texto sugerido numeral 2.
6. De los problemas que se encuentran en la sección 6-3, numerales 19, 20, 23, 24 y 25, resuelva la resistencia equivalente, en el texto sugerido en el numeral dos.
R5R410kR3100kR240k+V1R120k

61. MODULO 4
4. USO DEL SOFTWARE DE SIMULACIÓN CIRCUIT MAKER
INTRODUCCION
En muchas ocasiones, corroborar los resultados obtenidos de manera práctica, hace que el proceso de diseño y análisis sea tedioso, llevándonos a un desgastante, ineficiente y frustrante proceso de implementación; para evitar tales situaciones, el software se ha convertido en una herramienta de primera mano para los estudiosos de la electrónica.
Mediante un proceso de simulación podemos reproducir situaciones de laboratorio que permiten, antes de llevar los diseños y/o análisis al prototipo, verificar el funcionamiento de los circuitos, de ésta manera, el software siempre será una herramienta que facilita el proceso de diseño, más no es el fin, el objetivo primordial del estudio de las variables en la electrónica es la aplicación de conceptos, los procesos de diseño y análisis de circuitos eléctricos, herramientas fundamentales en el buen desempeño como profesionales en el área.
MAPA CONCEPTUAL

62. LOGROS
 Utilizar de manera adecuada el software de simulación (Circuit Maker y Multisim), para la comprobación de resultados obtenidos en el análisis y diseño de circuitos resistivos.
 Aplicar los conceptos de resistencia, voltaje, corriente y potencia en el diseño de circuitos resistivos, usando el software de simulación para la comprobación de los resultados obtenidos.
4.1. SIMULACIÓN CON CIRCUIT MAKER Y MULTISIM
Una alternativa muy práctica y económica para realizar la comprobación y análisis antes del montaje de los circuitos a diseñar, es el uso de software de simulación, en él mediante planos electrónicos, se someten a pruebas mediante señales de entrada, y con los instrumentos de un laboratorio convencional, se hacen las mediciones necesarias para su posterior montaje en el protoboard.
Analisis de Circuitos
Software de simulación
Circuitos resistivos
Serie
Paralelo
Mixto
Corriente
Voltaje
Potencia

63. Ladillo: El protoboard es una placa donde se hacen los respectivos montajes antes de ser pasados a una placa o circuito impreso. En la sección 2.6 se realiza su respectiva explicación.
Dos programas de fácil consecución en la red y uso son el Circuit Maker y el Multisim, el primero un desarrollo académico en la Universidad de Berkeley y el segundo de la compañía National Instruments, para familiarizarse con cada uno de ellos, se puede descargar de las páginas que se sugieren a continuación, dónde se encuentran las versiones estudiantiles y demo, con licencia para 30 días, también se pueden encontrar manuales y tutoriales en español de cada uno de ellos, usando el motor de búsqueda de su preferencia bajo el texto: “Manual de circuit maker” o “Manual de multisim”, se puede reemplazar la palabra Manual por Tutorial para obtener otra serie de documentos, el estudiante debe explorar cada uno de ellos, según sus intereses y recomendaciones del docente, sin embargo en ésta sección, se realizan 2 simulaciones una con cada uno de ellos, para familiarizarnos con el uso específico que se pretende para ésta materia.
El software de simulación, Circuit Maker, se puede descargar del Link: http://my.ece.ucsb.edu/bobsclass/2C/Simulation/circuit_maker.htm6 Junto con el manual en su versión en inglés y Work bench Multisim evaluation software http://www.ni.com/academic/multisimse.htm
A continuación se presentan dos simulaciones, una con cada uno de ellos, para que el estudiante se familiarice con el software dentro de las aplicaciones específicas que se pedirán más adelante
Ejemplo: Simulación de un circuito resistivo usando Circuit Maker:
6 Consultado el 27 de Diciembre de 2009, 1:30 PM

64. Inicialmente, después de haber realizado la instalación del software, se ubica en el botón inicio, dentro de la opción todos los programas, el acceso directo al software, como se muestra en el siguiente gráfico:
Figura 4.1 Opción de acceso inicial al software Circuit Maker
Después de ser usado con regularidad aparecerá dentro de los programas que se observan en el menú desplegable, al dar clic en el botón inicio. Al ingresar se observa la siguiente ventana:
Figura 4.2 Ventana Inicial de Circuit Maker
En la Figura 4.2, se observan las partes convencionales de una ventana, se debe prestar mucha atención a los íconos de la barra de herramientas, a partir de ellos

65. se realizará la simulación que se plantea, especialmente a los que se exponen a continuación en la Figura 4.3
Figura 4.3 Barra de herramientas para Circuit Maker
A continuación se hace una breve reseña del uso de cada uno de los íconos que se observan en ella:
Tabla 4.1 Listado de íconos barra de herramientas Circuit Maker.
Nueva simulación Abrir simulación existente
Guardar simulación
Imprimir Archivo
Herramienta selección
Herramienta Interconexión
Herramienta Texto
Borrado
Zoom
Rotar 90º
Expandir
Modo de simulación
Deshacer simulación Simulación, paso a paso
Simulación continúa
Punta de prueba Punta lógica
Gráficos de las señales
Selección de elementos
Buscar dispositivo Diseño de dispositivo
Ayuda
PCB Traxmarker

66. Inicialmente, se exponen paso a paso los íconos que se quieren usar específicamente en esta simulación.
El circuito que se pretende analizar es el que se expone a continuación, de él se deducen las variables de: Resistencia equivalente (Req), Voltaje (V), corriente (I) y Potencia (W), de cada una de las resistencias.
Para realizar el plano del circuito se da clic sobre el ícono “selección de elementos” , aparece una ventana como la que se muestra a continuación:
Figura 4.4 Ventana selección de elementos
Para seleccionar una resistencia, debemos dar clic sobre la opción “Resistors” que se observa en la lista bajo el titulo “Minor Device Class”, se debe tener especial cuidado de estar en la opción “General” como se observa en la primera lista del lado izquierdo. Una vez seleccionada la opción de resistencia, damos clic en el botón “Place”. Aparecerá la resistencia en el área de trabajo, realizamos el procedimiento tantas veces como resistencias necesitemos, para este caso, emplearemos 5 resistencias. Las ubicamos según la intencionalidad del circuito, como se observa en la Figura 4.5
Figura 4.5 Distribución de las resistencias en el área de trabajo

67. Las resistencias que están a la izquierda, se conectaran en serie, las resistencias R3 y R4 se conectaran en paralelo, para ello se seleccionan y se rotan 90 grados con el ícono: posteriormente, se selecciona el modo conexión, con el icono: y se realizan las conexiones necesarias como se muestra en la Figura 2.5.6. Para usar la herramienta de Interconexión, basta con acercar el cursor al elemento a conectar y dar clic sostenido, arrastrar hasta llegar al segundo punto y realizar la conexión necesaria.
Figura 4.6 Circuito resistivo
Para conectar la fuente de voltaje (V1 = 10V) y el punto de referencia, se usa el mismo ícono que aparece en la Tabla 2.5.1 que se usó para las resistencias: “Selección de elementos”. La fuente de voltaje aparece en la opción “Sources” en la columna: “Minor Divice Class” de la Figura 2.5.4 y seleccionando “Battery” en la columna “Device symbol” para el punto de referencia o tierra en la misma columna R51kR41kR31kR21kR11k

68. se selecciona la opción “Ground”. Al realizar la conexión el circuito queda como
aparece a continuación:
Figura 4.7. Circuito a analizar con fuente de voltaje.
Una vez realizado el montaje se debe verificar que los elementos están
conectados, para ello seleccionamos la opción “Check Pins Connections” del
menú de comandos, dentro de “Simulation”, si todos los componentes están
conectados aparecerá un mensaje que nos indicará si están bien conectados o no,
en la siguiente figura se muestra como acceder a dicha opción.
Figura 4.8.Verificación de conexión.
Para terminar la simulación, damos clic en el ícono “Simulación continua”, el
cual permite acceder al multímetro, siempre y cuando la opción de simulación esté
+ V1
10V
R5
1k
R4
1k
R3
1k
R2
1k
R1
1k

69. en modo análogo , no digital; se debe observar que la punta de prueba esté activa , al pasar a la zona de trabajo donde se encuentra el circuito, sobre el puntero en forma de punta de prueba, aparecen las letras V, P e I, según nos desplacemos sobre cada una de las resistencias, en el recuadro negro, aparecen las mediciones de cada variable, V = Voltaje, P = Potencia e I = Corriente, los datos se pueden corroborar si se hace el análisis, como se mostró en el ejemplo de el módulo 3.
Se sugiere realizar la exploración más profunda del software, al igual que el de Work Bench. Al descargar el software, puede tener acceso a los manuales y tutoriales, aunque en Inglés explican con más detalle cada función, sin embargo puede buscar documentos en Internet que le sirvan de guía en español, usando los motores de búsqueda como Google.
RESUMEN
El uso de software de simulación, es de gran importancia en los procesos de diseño, en éstos se puede corroborar los resultados obtenidos en la etapa de diseño, antes de llevarlos a la implementación de prototipos. Circuit Maker y Multisim, son herramientas que se encuentran en el mercado y que cuentan con versiones Demo, las cuales se pueden utilizar aunque con ciertas limitaciones. Como actividad académica se puede explorar cada uno de ellos desde esta perspectiva.
Queda en el estudiante explorar, no solo éstos en su versión completa, en la medida de las posibilidades, sino otros que encuentre en las fuentes de información que tenga a mano.
BIBLIOGRAFIA RECOMENDADA
INTERNET:
http://fresno.pntic.mec.es/~fagl0000/clasificacion.htm

70. http://www.unicrom.com/TuT_codigocolores.asp
http://my.ece.ucsb.edu/bobsclass/2C/Simulation/circuit_maker.htm
http://www.ni.com/academic/multisimse.htm
NEXO
El tema que se trato en el capítulo anterior es de fundamental importancia, en él se estudió el uso de una de las herramientas fundamentales en la electrónica y en muchas disciplinas tecnológicas. Aunque no se usa más que en lo necesario y pertinente en cuanto a la aplicación que compete al estudio de la electrónica básica, ésta herramienta debe ser usada y estudiada con mayor profundidad, no solo en los siguientes temas, sino en otros relacionados con el estudio de la electrónica.
Los programas de simulación, facilitan la implementación de circuitos, ya que antes de llevar el prototipo a un protoboard, se puede corroborar su funcionamiento mediante mencionada herramienta, ahorrando tiempo y dinero en el proceso de diseño, pues al detectar las posibles fallas, se replantea el diseño y se solucionan posibles inconvenientes que se llegasen a presentar.
SEGUIMIENTO AL AUTOAPRENDIZAJE
Realice la simulación de los ejercicios propuestos en la sección 3.1.2.2 usando Circuit Maker. Realice la comprobación de cada variable en el circuito y escriba sus resultados en una tabla, para corriente, voltaje y potencia sobre cada componente, incluyendo la fuente de Voltaje.

71. MODULO 5
5. USO DE INSTRUMENTOS
INTRODUCCION
Los elementos de cotidiano uso en el laboratorio, son y serán los que se deban usar en el contexto real, por ello se debe realizar un estudio concienzudo de éstos, pues de ello depende en muchas ocasiones el diagnóstico de fallas que podamos realizar en una aplicación específica o el correcto funcionamiento del diseño realizado.
En éste capítulo, se plantea el estudio de algunos instrumentos y elementos de laboratorio como el cautín, el protoboard y el multímetro. Debido a la aplicación funcional, no se profundiza en otros que serán tratados más adelante, como el caso del osciloscopio y el generador de señales, los cuales se trataran en el capítulo referente al condensador, dónde se aplican para determinar características propias en situaciones dónde se estudia dicho componente.
MAPA CONCEPTUAL

72. LOGROS
 Usar de manera adecuada el cautín, el protoboard y el multímetro, teniendo en cuenta las normas de uso y cuidados.
 Determinar las variables que intervienen en un circuito resistivo usando de manera adecuada el multímetro.
5.1 EL PROTOBOARD
El protoboard o tarjeta de prueba, es un elemento de laboratorio muy importante, en el se realizan los montajes de manera provisional, cada uno de los componentes del circuito se insertan en los orificios que éste tiene. Generalmente éste elemento está fabricado en plástico, en la Figura 5.1 se observa una fotografía que permite familiarizarnos con él. Los orificios son “Nodos” de conexión, los cuales obedecen a un patrón: los orificios verticales, tomando el protoboard como se muestra en la Figura 5.1, están conectados entre sí, los orificios horizontales son comunes entre sí, es decir son como un solo conductor, hasta donde se encuentra la letra “W”. Un ejercicio interesante
Instrumentos del laboratorio
Cautín
Normas de Uso
Cuidados
Protoboard
Normas de Uso
Cuidados
Fallas
Multimetro
Normas de Uso
Variables
Escala

73. se plantea en el uso del multímetro donde se determinan los patrones de
conexión
FIGURA 5.1 Diagrama esquemático de un protoboard
Tomado de: http://www2.ing.puc.cl/~dmery/arqui/el_protoboard.pdf
5.2 EL CAUTÍN
El cautín es otro de los elementos con los que debemos familiarizarnos,
también se conoce con el nombre de soldador, con él se aplica calor a la
soldadura, para que esta se adhiera a los elementos que queremos soldar,
generalmente conductores metálicos. Se debe tener especial cuidado en las
normas de seguridad al utilizar este elemento, pues al calentarse se convierte
en un objeto peligroso al utilizarlo de manera imprudente.
Figura 5.2. Fotografía de un cautín
Algunas cosas que debemos tener en cuenta son:
 Evite tocar la punta del cautín con los dedos, cuando se encuentre
conectado, debe ser prudente, pues puede estar caliente.
 Asegúrese de que las superficies a soldar están limpias.

74.  Aplique crema para soldar.
 Coloque la punta sobre la parte a soldar y luego acerque la soldadura.
 Espere a que la soldadura seque y luego verifique si ha quedado bien soldado.
 Una vez termine de soldar, desconecte el cautín y déjelo en un lugar seguro, mientras su temperatura disminuye.
5.3 EL MULTÍMETRO
Es uno de los elementos fundamentales del laboratorio, mediante éste instrumento se determinan las variables a medir, como voltaje corriente, resistencia, continuidad, capacitancia, inductancia entre otras muchas, dependiendo de la tecnología y el fabricante. Uno de los fabricantes pioneros y representativos en el mercado de éste dispositivo es “Fluke”, quienes han desarrollado múltiples alternativas en cuanto a éste y otros instrumentos de medida. Para su uso se sugiere leer antes el manual de usuario, sin embargo en esta sección se plantean algunas generalidades que se deben tener en cuenta en el momento de usar dicho instrumento.
 Primero debe leerse el manual de usuario y familiarizarse con su uso, identificar sus partes y funciones.
 Antes de realizar cualquier medición, se debe tener cuidado de graduar la perilla selectora en la unidad correspondiente.
 Al realizar las mediciones tener cuidado de no hacer contacto entre dos terminales que no deben conectarse, sobre todo si se está midiendo corriente, las puntas del multímetro deben colocarse con cuidado en los puntos donde se realiza la medición.
Figura 5.3 Fotografía de un multímetro.

75. En la primera parte del documento, se planteo descargar del siguiente link, sin embargo se plantea usarlo de nuevo, pues es uno de los más fáciles de utilizar, aquí se deja el link de nuevo:
http://assets.fluke.com/manuals/175_____umspa0100.pdf
Con dicho manual se pretende que el estudiante adquiera el conocimiento teórico antes de familiarizarse con el uso práctico, en las páginas 10 y 11, aparece la forma como se determina la corriente, el voltaje y la resistencia.
APRENDIZAJE COLABORATIVO:
Actividad:
Junto con sus compañeros, realice la siguiente práctica, usando el multímetro y el protoboard.
Para complementar el uso del multímetro y el protoboard, se sugiere realizar la prueba de continuidad de los orificios o “nodos” del protoboard, para ello siga los pasos que a continuación se describen:
a. Use el multímetro en modo continuidad, para ello identifique el ícono que se muestra a continuación:
Figura 2.6.4 I cono que indica escala de continuidad.

76. Si no lo encuentra, puede ser que su multímetro no posea dicha función en cuyo caso, debe buscar la escala de Ohmios, que generalmente aparece señalada con el símbolo: Ω. Si es así, mueva la perilla en esta escala hasta que señale el rango más bajo de resistencia.
b. Verifique el estado de las puntas del multímetro: Si su multímetro tiene la opción que se describió en la Figura 2.6.4, entonces al unir las puntas además de señalar en la pantalla de visualización 0.00 Ω, escuchará una señal audible; si no posee esta función solo aparecerá en la pantalla 0 Ω. Si al realizar este paso no sucede lo indicado, las puntas del multímetro están “abiertas”, en cuyo caso deben ser reemplazadas.
c. Tome las puntas y coloque un alambre en cada una de ellas, para poder introducirlas en el protoboard sin causar daños en éste. Empiece a realizar pruebas de tal forma que realice recorridos tanto en las líneas horizontales como verticales, para orientarse un poco, observe la Figura 2.6.1.
RESUMEN
La determinación de variables en los circuitos, son una aproximación al análisis de éstos, donde se plantea inicialmente reconocer las conexiones entre los dispositivos, las topologías genéricas son serie, paralelo y mixta. Las variables a analizar generalmente son de corriente, voltaje, potencia y resistencia en éste caso.
En el análisis de circuitos existen muchos elementos que permiten realizar la comprobación de dichos análisis, una de ellas son los programas de simulación, estos permiten que se haga la comprobación de los cálculos hechos en los circuitos. Aunque desde los mismos cálculos como se mostro en los ejemplos de circuito serie y paralelo, se puede realizar la comprobación de estos.

77. Si se hiciese el proceso de diseño de un circuito, lo primero que se debe indagar es por los requerimientos del diseño, a continuación se realizan los cálculos necesarios para luego hacer el montaje del prototipo, en protoboard haciendo las mediciones y comprobaciones en el laboratorio, finalmente se hace el montaje en placa o baquelita.
BIBLIOGRAFIA RECOMENDADA
INTERNET:
http://www.yoreparo.com/foros/electronica/soluciones/codigos-y-simbolos-en- electronica-con-videos-t186616.html
http://fresno.pntic.mec.es/~fagl0000/clasificacion.htm
http://www.unicrom.com/TuT_codigocolores.asp
http://books.google.com.co/books?id=LdzhG3XZd2IC&pg=PA73&dq=CLASIFCACION+DE+LAS+RESISTENCIAS#PPA72,M1
TEXTO:
ROBBINS, Allan. Análisis de circuitos Teoría y práctica. Cap.3. Cengace Learning. p. 51
NILSSON, James. Circuitos Eléctricos. Cap. 3. Pearson Prentice Hall. p. 66
NEXO
El análisis de los circuitos planteados, donde se halla la resistencia equivalente, es un primer paso para acercarnos al análisis de circuitos, tomando como referencia estos, se puede determinar otras variables, como corriente, voltaje, potencie entre otros, pues de ellos depende el análisis de los circuitos con elementos pasivos, como las bobinas y los condensadores, que se trataran más adelante.

78. El software de simulación que se explico en ésta sección, es un primer acercamiento, se puede usar en los subsiguientes capítulos, como herramienta en la comprobación de los cálculos hechos, teniendo presente que cada uno de estos, se actualiza con el tiempo o desaparece, por ello más allá de usar o no el software de simulación, se debe familiarizar con la estructura y funcionamiento de éste para así a futuro utilizar cualquier herramienta similar.
SEGUIMIENTO DE AUTOAPRENDIZAJE
Realice el montaje del siguiente circuito:
1. Desconecte la fuente de voltaje y mida la resistencia total.
2. Con la fuente de voltaje de 10V, calcule la corriente que debe pasar por R3.
3. Mida la corriente usando el multímetro.
4. Realice las mediciones de voltaje sobre cada resistencia y calcule la corriente que pasa por cada una de ellas, registre sus resultados en una tabla.
5. Calcule la potencia en cada una de las resistencias y sume los datos obtenidos.
6. Con el dato de corriente total y la fuente de voltaje calcule la potencia y compárela con el dato obtenido de la suma de las potencias.
R522kR410kR3100kR22.2k+V110VR11k

79. 7. Escriba las conclusiones obtenidas en la comparación de los resultados obtenidos con el instrumento y los cálculos realizados en un informe de laboratorio.

80. MODULO 6
6. CONDENSADORES
INTRODUCCION
En éste capítulo, se trata el efecto y uso del condensador, como elemento pasivo que tiene características específicas, que se pueden aprovechar en el tratamiento de la energía eléctrica. Inicialmente se hace una explicación sobre el concepto de capacitancia y el efecto en la energía eléctrica.
Los condensadores al igual que las resistencias, se denominas elementos pasivos, su principio de funcionamiento se explica a partir del campo eléctrico, y el movimiento de cargas entre dos placas paralelas donde se encuentra una diferencia de potencial.
Básicamente un condensador es un dispositivo capaz de almacenar energía en forma de campo eléctrico. Está formado por dos armaduras metálicas paralelas (generalmente de aluminio) separadas por un material dieléctrico.
Sus características más importantes son: capacidad, tensión de trabajo, tolerancia y polaridad, entre muchas de sus aplicaciones está el de bloqueo de corriente continua, acoplamiento de una señal de un sistema a otro, es decir para llevar una señal de un sistema a otro, por ejemplo si se quiere captar la señal de voz, para llevarla luego a un dispositivo electrónico, el condensador es uno de los elementos usados para tal fin; facilitar la conducción de corriente alterna, procesos de filtraje, sintonización, generación de ondas no senosoidales y almacenamiento de energía.

81. MAPA CONCEPTUAL
LOGROS
a. Aplica de manera adecuada el concepto de condensador al análisis de circuito serie, paralelo y mixto.
b. Identifica el fenómeno de capacitancia a dos placas paralelas, sometidas a una diferencia de potencial.
c. Reconoce los efectos resistivos, a partir de la reactancia capacitiva, en el análisis básico realizado a un circuito serie, paralelo y mixto con condensadores.
d. Identifica las principales aplicaciones del condensador dentro de la electrónica.
6.1. PRINCIPIOS FÍSICOS
Desde la física, existen algunas leyes y teorías relacionadas, que permiten el entendimiento del funcionamiento de un condensador, una de ellas es la del campo eléctrico y la carga del electrón, sin profundizar demasiado, se pretende explicar de manera practica el cómo se dan estos dos conceptos en un condensador. Inicialmente, se parte del principio de que dos placas paralelas, están sometidas a un voltaje o potencial, como se muestra en la Figura 6.1.1, como se observa, las cargas positivas se “mueven” hacia la placa con carga
VARIABLES
NO
POLARIZADOS
ELECTROLITICOS
FIJOS
CLASIFICACION
CARGA
ELECTRICA
CAMPO
ELECTRICO
CONDENSADOR
ALMACENAMIENTO
SINTONIZACION
ACOPLE
FILTRAJE
APLICACIONES
MULTIMETRO
NOMENCLATURA
MEDICION
CAPACITANCIA

82. negativa, debe recordarse, que la carga positiva obedece al efecto causado por la falta de electrones, mientras que la carga negativa, obedece al exceso de electrones, el potencial o voltaje debe ser suficiente para llevar que la carga pase de una a otra placa, vencer ese espacio, si en el espacio que está en las placas es el vacio, la carga tendrá un movimiento más libre, pero si en medio hay un material conocido como dieléctrico, entonces, se puede “almacenar” por un periodo de tiempo muy pequeño una carga, pues esta queda “atrapada”.
Figura 6.1.1 Condensador de placas paralelas
Si se quiere realizar una revisión más profunda sobre la teoría que se aplica en la explicación del comportamiento de este dispositivo, se sugiere revisar la ley de Gauss y la ley de Coulomb, en la bibliografía sugerida.
La capacitancia está dada como la proporción que existe entre el área de las placas (A) y la distancia que las separa (d), por las constantes de permitividad eléctrica ( y la constante dieléctrica (k) del material que existe entre las placas, de tal forma que la ecuación de la capacitancia está dada por:
Ecuación 6.1.1
El dieléctrico busca aumentar el valor de la capacitancia, es decir la propiedad de almacenar cierto potencial en un tiempo muy corto, cabe aclarar que ese tiempo

83. depende además de la configuración circuital y que depende del valor de la capacitancia, de manera práctica existe una forma de identificar éste tipo de dispositivos tanto por inspección como por instrumentos.
La unidad de medida usada para la capacitancia es el Faradio, en honor a Michael Faraday, aunque se usan comúnmente los submúltiplos, pues para obtener valores de condensadores del orden de los Faradios se deberían usar unas placas paralelas con áreas extremadamente grandes como se muestra a continuación: De la Ecuación 3.1.1. se despeja el área, para determinar que tan grandes deben ser dichas placas, si la distancia entre las placas es de 1 mm, se tiene que:
K = 1 para el vacio
. (Permitividad del espacio libre) se reemplazan dichos valores en la siguiente fórmula:
Es decir 112.000.000 m2. Como se puede observar el área ha de ser muy grande para que nuestro condensador tenga una capacitancia de 1 Faradio, por tanto los valores comerciales más comunes están en el orden de: micro faradios (μf), nano faradios (nf), pico faradios (pf) etc.
El efecto del dieléctrico, hace que la capacitancia aumente, por ello se usan algunos materiales entre las placas, se puede deducir fácilmente, si se observa detenidamente la Ecuación 6.1.1., pues la constante dieléctrica, es un factor multiplicativo de la capacitancia. Algunos materiales se pueden observar en la siguiente Tabla.
Tabla 6.1.1. Constante dieléctrica de algunos materiales usados como dieléctrico en condensadores.
Material
K

84. Vacio
1
Aire
1,0006
Teflón
2
Poliestireno
2,5
Mylar
3
Papel parafinado
4
Mica
5
Oxido de aluminio
7
Oxido de tantalio
25
Cerámica (k pequeña)
10
Cerámica (k grande)
100 - 10000
Tomado de: KAUFMAN, Milton. Electrónica moderna práctica. México: Mc Graw Hill, 1995. p. 2-3.
Actividad:
Use la tabla 3.1.1 para hallar la capacitancia de un condensador con las siguientes características, cambiando el material dieléctrico.
A = 3 mm2
d = 0,5 mm
Material dieléctrico:
a) Oxido de Tantalio
b) Cerámica (k=130)
c) Oxido de aluminio
d) Mica
e) Poliestireno
6.2. CLASIFICACIÓN DE CONDENSADORES
Los condensadores, se pueden clasificar en dos grandes grupos, los cuales se explican a continuación y aunque existe una gran gamma de estos dispositivos,

85. para los propósitos del curso, se platea el conocimiento de los expuestos a continuación.
6.2.1. VARIABLES:
Son condensadores que pueden cambiar su valor de capacitancia, ya que en su estructura tienen un elemento variable o cursor, que permite modificar dicho valor, un ejemplo de ellos, son los sintonizadores de emisoras en los radios análogos, donde una perilla, permitía cambiar de una emisora a otra. Entre otros se encuentran:
De ajuste fino: Usan algunos dieléctricos como aire, cerámica, mica, cuarzo, entre otros.
Varactores: Son dispositivos electrónicos que aprovechan el efecto capacitivo de un semiconductor, en realidad son semiconductores, los cuales se explicaran más adelante, entre las múltiples aplicaciones se encuentra: en comunicaciones (microondas), sintonizadores de TV, multiplicadores de alta frecuencia y como controladores de frecuencia. Específicamente, para los varactores, el símbolo usado es:
Figura 6.2.1.1 Símbolo usado para los varactores
Como se puede Observar, además del condensador, esta asociado otro dispositivo, éste es un diodo, el cual se estudiará en la sección de los semiconductores.
El símbolo que se encuentra de los condensadores variables, en los planos electrónicos es:
D2BBY31D1BBY31

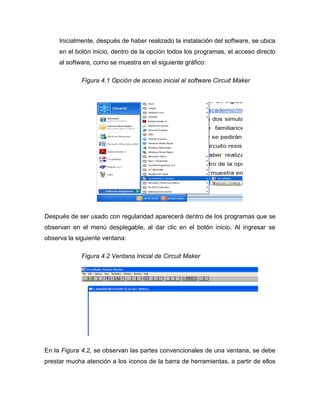
86. Figura 6.2.1.1 Símbolo de un condensador variable.
6.2.2. FIJOS:
Como su nombre lo indica, son condensadores cuyo valor no puede ser
modificado, es el fabricante quien define el valor de dicho condensador, existen
diferentes formas de identificar a dichos condensadores, como se explicará en la
siguiente sección. Dentro de éste grupo se encuentran dos clases, las cuales son:
6.2.2.1. POLARIZADOS:
Son condensadores que tienen definido un terminal positivo y un terminal
negativo, se debe tener mucho cuidado al conectarlos en un circuito, pues de no
hacerlo correctamente, pueden explotar. Los condensadores polarizados, permiten
identificar su valor de capacitancia, el terminal negativo y el voltaje para el cual es
diseñado, dichos datos vienen impresos en su carcasa.
Figura 6.2.1. Condensador polarizado
Tomado de: http://micromotores.com/productos/images/350-210-050.gif [Cit. 29
Dic. 2009]
En la Figura 6.2.1, se observa un condensador electrolítico, en el se diferencia el
terminal negativo, por la franja negra que tiene y el valor de su capacitancia:
2200μf @ 16 V, es decir el voltaje que podemos aplicar es de 16 Voltios,
C1
1uF

87. preferiblemente, aunque no quiere decir que pueda trabajar con voltajes
levemente cercanos, se prefiere que su punto de operación esté muy por debajo
del estipulado por el fabricante.
El símbolo para estos condensadores se muestra en la Figura 6.2.1.2:
Figura 6.2.1.2 Símbolo de un condensador polarizado
El terminal positivo es la línea recta y el negativo la línea curva, en muchas
ocasiones, el terminal negativo se indica con una línea más gruesa.
Cabe anotar que un condensador electrolítico, nunca debe ser conectado en una
fuente alterna, por obvias razones, éste se polariza en inverso en el semiciclo
negativo de la señal, como se indica en la sección correspondiente al
comportamiento en AC.
6.2.2.2 NO POLARIZADOS:
Son condensadores fijos que no tienen polaridad, al conectarlos se puede hacer
de manera indistinta, cualquiera de sus dos terminales. En la siguiente sección se
explica cómo identificar su capacitancia, a partir de los códigos generados para tal
fin.
Figura 6.2.2.2.1 Condensador No polarizado
+
C1
1uF

88. Tomado de: http://www.ucontrol.com.ar/condensadores/_CondensadorCeramico.jpg
[Cit. 29 Dic 2009]
Existe una gran variedad de condensadores no polarizados, al igual que códigos para su identificación, por ello el clasificarlos es tan importante como el reconocer su función, en la sección 3.3 se realiza una breve explicación de cómo usar algunos códigos en la determinación del valor de la capacitancia.
El símbolo asociado a este tipo de condensador se observa en la Figura 6.2.2.2.2
Figura 6.2.2.2.2 Símbolo de un condensador no polarizado.
Actividad:
Como complemento y afianzamiento de los temas tratados hasta aquí, se recomienda, hacer lectura del texto que se encuentra en el Link: http://books.google.com.co/books?id=PW7jBPNU8hwC&pg=PA145&dq=condensador+electrolitico&cd=2#v=onepage&q=&f=false paginas 143 a 146
6.3. MEDICIÓN
Al igual que las resistencias, los condensadores se pueden identificar de dos maneras, una por los códigos y convenciones usadas a nivel internacional y otra a partir de los instrumentos tanto una como otra tiene sus pros y sus contras. Al hacerlo por nomenclatura, el principal inconveniente radica en el hecho de que existen múltiples nomenclaturas, dependiendo del condensador y de la aplicación de éste, por otro lado se corre el riesgo de no interpretar bien el código o que éste esté deteriorado, en cuyo caso se realizaría una lectura errónea. En cuanto al manejo de instrumentos, la limitante radica en el uso del instrumento, su precisión y buen estado, al igual que la interpretación de la medida. Se sugiere que se esté
C11uF

89. familiarizado tanto con uno como con el otro método, pues en muchas situaciones uno puede ser verificación del otro y ofrecer así una mejor interpretación de la medida.
6.3.1. DETERMINACIÓN POR NOMENCLATURA
Dependiendo del tipo de condensador se encuentran las siguientes tablas de equivalencia y su respectiva interpretación, según la clase de condensador y aplicación se tiene que:
Figura 6.3.1 Tabla código de colores para algunos capacitores de poliéster.
Tomado de: www.neoteo.com/ [Cit. 28 de Dic de 2009]
Como se puede observar, el código de colores es el mismo que se usa con las resistencias de 5 bandas o de precisión. Su interpretación aunque es muy sencilla, se explica con un breve ejemplo.

90. Ejemplo: Se quiere determinar la capacitancia de un condensador cuyos colores son los que aparecen en la siguiente tabla:
Tabla 6.3.1. Ejemplo de capacitor de poliéster
Color
Valor
Amarillo
4
1 cifra
Verde
5
2 cifra
Violeta
7
3 cifra
Naranja
5
Tolerancia
Rojo
250
Voltaje
Una vez detectado el significado de cada cifra, se realiza su interpretación: las tres primeras cifras, corresponden al valor del condensador la cuarta es la tolerancia y la última el voltaje de operación, por tanto el valor del condensador es:
457 pico faradios (pf), 5% de tolerancia y un voltaje de trabajo de 250 V. La tolerancia es el valor que el fabricante garantiza para la capacitancia del condensador, como se explico en la sección correspondiente a las resistencias, se tiene que:
El 5% de 457 es: 22.85, este valor se suma y se resta al valor del condensador, luego el valor que el fabricante garantiza está entre: 479,85 y 434,15. Se debe tener especial cuidado pues el valor del condensador esta dado en pico faradios, sin importar el numero al cual se llegue, por otro lado, observe que si el valor de la capacitancia está por debajo de los 10 pf, la tolerancia se da en picofaradios, pero si dicho valor es mayor a 10 pf, entonces la tolerancia se da en porcentajes, tal como aparece en la tabla.
APRENDIZAJE COLABORATIVO:
Actividad:

91. Use la figura que se muestra a continuación, interprete la información dada para determinar la capacitancia de un condensador y escriba 5 ejemplos. Comparta los ejercicios propuestos y envíelos a sus compañeros como ejercicios, revíselos y reenvíe las correcciones hechas.
Figura 6.3.2. Tabla ejercicio de interpretación de capacitancia.
Tomado de: http://www.ucontrol.com.ar/wiki/index.php/Condensador [Cit. 28 Dic de 2009]
Otros condensadores, tiene impreso su valor en su carcasa, se les conoce con el nombre de lentejas o condensadores cerámicos, además del número, tienen una letra, la cual sirve para identificar su tolerancia, con el siguiente ejemplo se explica cómo usar dicha nomenclatura:
Ejemplo: Si el condensador tiene impreso el número 101, quiere decir:
101 = 10 + 1 cero = 100 pf.
104 = 10 + 4 ceros = 10.000 pf. = 0,1 μf.
Adicional al valor de la capacitancia, aparece una letra junto a éste, dicha letra representa la tolerancia, concepto que se ha venido explicando ampliamente

92. durante todos los capítulos, en la siguiente tabla, aparece la interpretación de cada letra.
Tabla 6.3.2 Condensadores cerámicos
Tomado de: http://www.ucontrol.com.ar/wiki/index.php/Condensador [Cit. 28 de Dic. De 2009]
Los condensadores de polyester son usados en aplicaciones donde se exige una alta inmunidad al ruido y eficiencia en cuanto a su voltaje de operación, dichos condensadores al recibir un exceso de tensión, hace que el metal rodee la perforación y permita que el condensador continúe operando.
6.3.2. DETERMINACIÓN POR INSTRUMENTO
Para determinar la capacitancia de un condensador se usa un multímetro diseñado para éste fin, es decir un multímetro con capacímetro. Colocando las terminales del condensador en el multímetro, éste nos da la lectura de la capacitancia. Una limitante es el rango para el cual está diseñado dicho capacímetro, aunque hoy en día se ha mejorado en dicho aspecto, hay algunos que solo pueden medir cierto grupo de condensadores.
Figura 6.3.2.1 Medición de capacitancia mediante multímetro.

93. Tomado de: Manual de uso Multímetro Models 175
En muchos multímetros se implementa unos orificios especiales donde se insertan las terminales del condensador, en lugar de hacerlo con las puntas como se muestra en la Figura 6.3.2.1.
6.4. COMPORTAMIENTO EN AC Y DC
Los condensadores, presentan diverso comportamiento al ser sometidos a estímulos de corriente o voltaje Alterno o Directo, aunque no se profundiza en el análisis de éstos, se pretende realizar una breve descripción de éste, como se muestra a continuación:
6.4.1. COMPORTAMIENTO EN AC:
Bajo corriente alterna, el condensador debe responder a las características de una señal AC, dichas características se mostraron en la Sección 1.6, la más importante en éste caso es la de la dualidad en los semiciclos positivo y negativo, al igual que el efecto de la frecuencia, en la Figura 1.6.1.1 se mostró una señal senosoidal, en la siguiente figura se realiza la explicación de su efecto en un capacitor. Partimos del hecho de que el condensador se encuentra descargado, como muestra la Figura 6.4.1.1 Debe observarse que el condensador no debe ser electrolítico, pues en el semiciclo negativo queda polarizado en inverso.

94. Figura 6.4.1.1 Condensador polarizado directamente
Se observa el circuito “alimentado” con una fuente alterna, en éste caso,
el condensador se carga hasta el valor máximo de la fuente, en el
semiciclo negativo, el condensador invierte la polaridad en sus placas, se
carga nuevamente hasta el valor mínimo para luego descargarse, el
efecto de la resistencia es limitar la corriente.
Figura 6.4.1.2 Efecto de un condensador en AC
Como se puede observar, el condensador invierte la señal de entrada, en
el gráfico la señal de entrada es la función seno (Negro) y la salida la
función coseno (Azul), dicho efecto de retraso en la señal es causado por
B
A
C1
0.2652nF
60 Hz
V1
-110/110V
R1
1000k
A
B
0 13.9m 27.8m 41.7m 55.6m 69.4m 83.3m
-12u
-8u
-4u
0
4u
8u
12u
Xa: 4.416m Xb: 21.15m
Yc: 11.02u Yd:-11.07u
a-b:-16.74m
c-d: 22.09u
freq: 59.75
Offsets X: 0.000 Y: 0.000
Ref=Ground X=13.9m/Div Y=current
d
c
a b
A
B

95. el condensador. Para observar la gráfica, se uso el software de simulación, Circuit Maker. Los datos que aparecen en la parte superior, corresponden a los cursores A, B, C y D, respectivamente, los cursores A y B corresponden a datos del eje horizontal y los cursores C y D, corresponden al eje vertical, a continuación, se hace una transcripción de la tabla de dichos datos:
Xa = 4,416 m
Xb = 21,08 m
a – b = 16,67 m
freq = 60.00
Yc = 11,02 u
Yd = 11,07 u
c –d = 22,09 u
En el eje horizontal se ubican los datos de tiempo y en el vertical los de corriente, como se puede apreciar, los datos de tiempo están en milisegundos (ms) y los de corriente en micro Amperios (uA), la diferencia entre los dos cursores aparece en la tercera columna, para hallar la frecuencia se usa la Ecuación 1.6.1.1, que es la inversa del periodo. El efecto que causa un condensador a una señal alterna, se denomina desfase, dicho desfase depende de los valores que tome el condensador y la resistencia.
Los valores para el condensador y la resistencia, fueron calculados mediante la ecuación de reactancia capacitiva, en la sección 3.5, se explica más detalladamente la interpretación de ésta, sin embargo, el estudiante, puede hacer una pequeña comprobación, cambiando el valor del condensador y realizando la simulación.
6.4.2. COMPORTAMIENTO EN DC:
Al polarizar el condensador, las cargas se acumulan entre las placas, pues se comporta como si estuviese abierto el circuito, debido al dieléctrico entre las placas, al desconectarse la alimentación, se presenta una diferencia de potencial por la acumulación de electrones en la placa conectada al negativo y

96. R1
100kΩ
C1
1μF
V1
10 V
J1
Key = Space
XSC1
A B
Ext Trig
+
+
_
_ + _ R1
100kΩ
C1
1μF
V1
10 V
J1
Key = Space
XSC1
A B
Ext Trig
+
+
_
_ + _
de huecos por la placa conectada al positivo. Si se unen los terminales el
condensador se descarga y vuelve a su condición inicial, en muchos casos,
para facilitar el análisis de circuitos se dice que el condensador se comporta
como un circuito abierto en DC, no hay flujo de electrones o corriente, pero si
hay un voltaje elevado igual a la diferencia de potencial entre sus terminales de
alimentación.
En la siguiente simulación, se puede observar con más detalle el efecto que
causa el condensador ante una fuente de voltaje directo o DC. Se usa el circuito
que se muestra en la Figura 6.4.2.1
Figura 6.4.2.1 Circuito condensador DC
Inicialmente el switch, que en el circuito se identifica con la letra J1, está
conectando la fuente de voltaje de 10 V, el condensador se carga (Derecha), y
cuando cambia de posición, el condensador se descarga (Izquierda), pues lo
conecta a tierra a través de la resistencia R1 de 100kΩ. Los gráficos de carga y
descarga se observan a continuación.
Figura 6.4.2.2 Gráfico de carga del condensador.

97. Los cursores o líneas que limitan el tramo de la gráfica, indican la sección de carga del condensador en la simulación. Para obtener ésta se usa el osciloscopio del software Multisim de National Instruments, que se descargó en la sección de uso de un simulador. Los datos que los dos cursores arrojan se observan en la Figura 6.4.2.3 en ella se observa los dos parámetros para “X” y para “Y”. Los valores de “Y” corresponden al voltaje y los de “X” corresponden al tiempo.
Figura 6.4.2.3 Tabla de valores para los cursores en la carga
Y1 corresponde al valor máximo de carga, Y2 corresponde al valor mínimo, como se puede observar el valor de carga es igual al voltaje de la fuente. Aunque se esperaría que el voltaje de carga sea constante, por efectos de la resistencia y de la capacitancia el condensador empieza a descargarse, pues almacena el potencial por un periodo de tiempo muy corto. El diferencial de “x” (dx), que se observa en la tabla, me permite determinar la diferencia entre x2 y x1, obteniendo así el tiempo de carga del condensador, en este caso es de 659,16 ms (milisegundos), este dato se compara más adelante con el tiempo de descarga.
A continuación se analiza la descarga del condensador. En la Figura 6.4.2.4, se limita con los cursores la sección correspondiente a la descarga. Observe que los datos de amplitud y1, corresponden a y2 del gráfico anterior.
Figura 6.4.2.4 Gráfico de descarga

98. Por simple inspección se puede observar que la sección del gráfico correspondiente a la descarga es más pequeña que la que se observa en la carga. Para continuar con el análisis de tiempo, se observa la información correspondiente a los cursores en la siguiente figura.
Figura 6.4.2.5 Tabla de valores para los cursores en la descarga.
En este caso el diferencial de x (dx) es de 404,84 ms (milisegundos). El efecto del gráfico inverso, donde se supone se está descargando el condensador, es debido al cambio de polaridad en las placas del condensador. Para hallar la constante de carga del condensador se usa la ecuación:

99. Para que el condensador obtenga el 98% de la carga de voltaje, según la fuente de alimentación, en éste cado que su carga sea de 9.8 Voltios, se requiere que transcurran 5 si se halla se tiene que es igual a 100 ms, multiplicando el valor del condensador y el valor de la resistencia, luego a los 500 ms aproximadamente, se tendrá el 98% de la carga de voltaje en el condensador, según la fuente de alimentación, si se observa la tabla de la Figura , se puede determinar que a más de 600 ms, la carga es cercana al 99,8% que es el valor máximo de carga para éste caso, muy difícilmente se obtendrá un 100%, debido a las perdidas y consumo de voltaje de los dispositivos del circuito.
Como se puede inferir, el efecto del condensador en DC, se puede aprovechar como elemento temporizador, pues el tiempo de carga y de descarga, me permite detectar un ciclo, de hecho en muchas aplicaciones se usan los condensadores como elementos de temporización o de “reloj”, por la unidad de tiempo que se usa.
6.5 REACTANCIA CAPACITIVA
La reactancia capacitiva, permite asociar el efecto resistivo de un condensador a un circuito, esto facilita el análisis de circuitos mediante estos elementos, y es dependiente de la frecuencia angular y el valor de la capacitancia, como se muestra en la Ecuación 6.5.1
Ecuación 6.5.1
La unidad de medida de la reactancia capacitiva es el Ohmio. Al reemplazar cada condensador por su equivalente mediante esta ecuación, cada reactancia puede ser tratada como una resistencia y hacer el análisis del circuito como si fuese resistivo. De esta manera, se pueden determinar los voltajes, corrientes y potencias del circuito, mediante las leyes estudiadas en las secciones anteriores.
Se observa que en la ecuación aparece el componente de frecuencia, el cual permite determinar el ángulo de desfase, en los conceptos revisados desde la física, para el movimiento armónico simple, se sabe que la frecuencia angular, es

100. la relación entre el ángulo recorrido y el tiempo empleado para dicho recorrido, si observa el gráfico empleado para explicar una función alterna (Figura 1.6.1.1), la circunferencia barrida, se puede determinar en función del ángulo. La frecuencia angular (ω) es proporcional a la frecuencia (f) y al ángulo en radianes (2π).
Ecuación 6.5.2
Para que exista el desfase en las señales AC, se asume una frecuencia, por ejemplo 60Hz, y se reemplaza en la Ecuación 3.5.1, se reemplaza la reactancia capacitiva Xc por el valor de la resistencia y se despeja la capacitancia. De esta manera se obtiene el desfase observado en la Figura 3.4.1.1. En el ejemplo realizado, dicho desfase fue de 90º.
Aprendizaje colaborativo
Actividad:
Use la formula de reactancia capacitiva y deduzca diferentes valores de capacitancia, si se quiere obtener una gráfica como la observada en la Figura 6.4.1.2, para resistencias de:
a) 1 KΩ
b) 50 KΩ
c) 1 MΩ
d) 130 KΩ
e) 500 KΩ
Envíe sus respuestas a un compañero e intercambien ideas sobre los resultados obtenidos. Realicen un informe sobre la actividad y conclusiones obtenidas
RESUMEN

101. Los condensadores son elementos pasivos, como las resistencias, sin embargo su comportamiento en AC o DC, es diferente. Cabe anotar que en el anterior capítulo solo se trato su concepto.
Un condensador como su nombre lo indica condensa un potencial, que a diferencia de una batería (quien lo genera debido a procesos químicos o eléctricos) o celda fotovoltaica, lo hace por muy corto tiempo. Consiste en un dispositivo de placas paralelas el cual se clasifica según su estructura y material empleado, en la fabricación, el cual se da según la aplicación para la cual fue diseñado.
La propiedad física que explica su funcionamiento se denomina capacitancia, asociada a éste se da el concepto de reactancia capacitiva, el cual se tratara más adelante.
BIBLIOGRAFIA RECOMENDADA
INTERNET:
http://es.wikipedia.org/wiki/Condensador_el%C3%A9ctrico
MULTIMEDIALES:
http://www.tu.tv/videos/carga-electrica-condensadores
http://www.tu.tv/videos-ext/43166008-campo-electrico-de-un-condensador
NEXO
En éste capítulo se estudió, el efecto capacitivo y su efecto en los dispositivos electrónicos, llamados capacitores o condensadores; dichos dispositivos son utilizados de manera amplia en el mundo de la electrónica, aprovechando sus características de almacenamiento de carga en tiempos muy cortos. A

102. continuación se usa dicho concepto en la asociación de condensadores, herramienta muy útil a la hora de analizar situaciones donde aparecen interconectados condensadores en las topologías serie, paralelo y mixto, como se mostró en el capítulo correspondiente al de resistencias.
En la teoría de control y modelamiento de sistemas dinámicos, se revisa éste concepto nuevamente, aplicando no solo su comportamiento como elemento pasivo, sino su respuesta a señales de entrada, tanto continuas como discretas.
Cabe pues señalar que el condensador no es de uso amplio en diferentes situaciones de estudio desde la electrónica. Queda pendiente un estudio profundo de su comportamiento en AC, el cual se retomará en la materia de circuitos fasoriales, en los semestres siguientes.
SEGUIMIENTO AL AUTOAPRENDIZAJE
1. Determine en los siguientes casos, el valor de la capacitancia de cada condensador:
a) 104 H
b) 103 Z
c) 105 D
d) 101 J
e) 474 M
2. Realice la simulación del circuito que se observa en la Figura 6.4.1, luego de obtener los gráficos que se aprecian en la Figura 6.4.1.2, cambie los valores del condensador o la resistencia, observe que pasa con el gráfico y explique con sus propias palabras la función del condensador en una señal AC. Apoye su análisis con la explicación de la sección 6.5 y aplique la ecuación correspondiente a la reactancia capacitiva.
3. Realice el montaje de la Figura 6.4.2.1, aplique la ecuación respectiva, que representa la carga y descarga del condensador para obtener 10 valores de

103. tiempo consecutivo, registre los resultados en una tabla y analice la relación entre los valores obtenidos de resistencia, capacitancia y tiempo.
MODULO 7
7. CONDENSADORES EN SERIE, PARALELO Y MIXTO
INTRODUCCION

104. Las múltiples aplicaciones del condensador en la electrónica hacen que su estudio no solo sea necesario, sino interesante, por ello se sugiere especial atención a éste tema, ya que en las comunicaciones, la instrumentación electrónica, el control y en muchas situaciones, el condensador coincide con los modelos matemáticos obtenidos para el estudio de éstas.
En el éste capítulo se plantea el estudio de la asociación de condensadores, en las topologías serie, paralelo y mixto, como se hizo en su momento con las resistencias. Los condensadores son elementos pasivos de uso generalizado en la electrónica, en muchas oportunidades se encontrará en situaciones donde se aplica el concepto de éste, bajo modelos en los cuales el simplificar, se hace que el análisis de dichas situaciones sea más sencilla.
Como complemento se plantea el estudio de dos elementos del laboratorio, el osciloscopio y el generador, con los que se puede determinar de manera indirecta el valor de la capacitancia y su comportamiento en AC, en el laboratorio.
MAPA CONCEPTUAL
Asociacion de condensadores
Topologías
Serie
Paralelo
Mixto
Medición en el laboratorio
Generador de señales
Osciloscopio

105. LOGROS
 Aplicar las ecuaciones que caracterizan la simplificación de las topologías: serie, paralelo y mixto de condensadores.
 Utilizar de manera adecuada el osciloscopio y el generador de señales, para determinar el comportamiento de ése en AC.
 Aplicar los conceptos obtenidos al montaje propuesto para la determinación del comportamiento del condensador en AC y en DC.
7.1. ASOCIACIÓN DE CONDENSADORES
Así como las resistencias, los condensadores se pueden asociar de la misma manera, en circuito serie, paralelo y mixto, donde se puede determinar inicialmente la capacitancia total, en esta sección no se profundizará en el cálculo de voltaje, corriente y potencia, pues hace parte de un curso especifico de análisis de circuitos, solo se hará referencia al efecto del dispositivo de manera conceptual.
http://es.wikipedia.org/wiki/Condensador_el%C3%A9ctrico
Las configuraciones en este caso son:
7.1.1 SERIE:
Los condensadores en serie, se tratan como si fuesen resistencias en paralelo, pero sin llegar al extremo de considerarlos como tales; es decir, su efecto aunque se puede asociar al de una resistencia, como se observa en la reactancia capacitiva, no se comportan de manera idéntica. La ecuación para determinar la capacitancia equivalente en la configuración en serie de condensadores esta dad por:
Ecuación 7.1.1.1

106. En el siguiente ejemplo se realiza un análisis para que el estudiante se ilustre de mejor manera.
Ejemplo: Halle la capacitancia equivalente del siguiente Circuito:
Figura 7.1.1.1 Condensadores en serie
Según la Ecuación 7.1.1.1, para éste caso se reemplazan los valores de las capacitancias y se despeja para Ceq. Se debe tener en cuenta que la capacitancia equivalente, se encuentra en el denominador, por tanto al desarrollar la ecuación debe “Invertirse”, para poder despejar dicha capacitancia.
Para determinar la capacitancia equivalente, se invierte el resultado y se obtiene el siguiente resultado:
Actividad
Halle la capacitancia equivalente en cada caso:
A.
C11/2 uFC27/8 uFC315/4 uFCeq

107. B.
C.
D.
7.1.2. PARALELO:
Los condensadores en paralelo, se pueden asociar a las ecuaciones usadas
como resistencias en serie, como se mencionó en el apartado anterior, no se
comportan como resistencias, la ecuación que rige el comportamiento de los
condensadores en paralelo es:
Ecuación 7.1.2.1
las capacitancias se suman como se muestra en el ejemplo correspondiente.
C1
2μF
C2
43000μF
C3
1800μF Ceq
C1
2μF
C2
4μF
C3
16μF Ceq
C1
10μF
C2
0.1μF
C3
0.01μF Ceq
C1
7μF
C2
14μF
C3
21μF Ceq

108. Figura7.1.2.1 Condensadores en paralelo
Según la Ecuación 7.1.2.1, para los condensadores que se observan en la Figura
7.1.2.1, se tiene que:
La capacitancia equivalente total es 1120
Aprendizaje colaborativo
Actividad:
Halle la capacitancia equivalente en cada caso, envié sus respuestas a sus
compañeros, discuta los resultados obtenidos y plantee situaciones similares, para
intercambiarlos entre sus compañeros.
A.
B.
C.
C1
470μF
C2
550μF
C3
100μF
C3
100uF
C2
100uF
C1
100uF
C4
50uF
C3
50uF
C2
1000uF
C1
1000uF

109. D.
7.1.3. MIXTO:
En éste caso, el análisis de esta topología, se realiza siguiendo un
procedimiento, sin seguir una ecuación particular, aunque se puede llegar a
inferir de manera lógica.
Figura 7.1.3.1 Condensadores configuración Mixta
Para resolver éste problema, se parte identificando el tipo de conexión que
tiene cada condensador, ya sea serie o paralelo. Se resuelve paso a paso y
se va reduciendo hasta llegar a un solo condensador. Se parte resolviendo
el paralelo que aparece al final de la configuración, condensadores C3 y C4,
se usa la Ecuación 7.1.2.1.: C3+C4=20μf, quedando como resultado la
configuración que aparece a continuación:
C4
1000nF
C3
1000nF
C2
500nF
C1
500nF
C8
1000nF
C7
1000nF
C6
500nF
C5
500nF
C4
500nF
C3
500nF
C2
500nF
C1
500nF
C4
10uF
C3
10uF
C2
100uF
C1
100uF

110. Figura 7.1.3.2 Configuración resultante
Para resolver esta parte, se usa la Ecuación 7.1.1.1, se obtiene como resultado:
Para terminar, solo basta invertir el resultado y se obtiene:
Para reforzar el concepto, se sugiere realizar la siguiente actividad:
7.2. MANEJO DE INSTRUMENTOS:
En esta sección, se plantea el uso del generador de señales y del osciloscopio, para determinar variables en una señal de tipo senosoidal.
7.2.1. EL GENERADOR DE SEÑALES Y EL OSCILOSCOPIO
El generador de señales, como su nombre lo indica, es un instrumento del laboratorio muy importante, pues con él se puede realizar una serie de pruebas, las cuales facilitan el diagnóstico de fallas o la emulación de un circuito sintonizado. Mediante éste se pueden generar 3 clases de señales a saber: función seno, triangular o diente de sierra y rectangular, modificando las características de frecuencia y amplitud, como funciones principales de dicho instrumento.
Figura 7.2.1.1 Generador de señales.
Ceq120uFC2100uFC1100uF

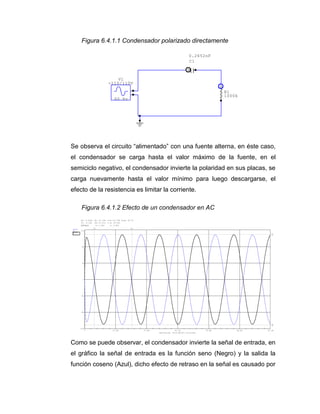
111. Tomado de: http://www.promax.es/esp/products/fotoprod.asp?filename=GF- 23x.jpg [Cit. Dic 29 de 2009]
Cada botón del generador permite variar las características de la señal, en ésta sección, se explica brevemente las funciones pertinentes para el curso, pero es el estudiante quien debe estudiar a profundidad las que se explican en el manual del instrumento. La mayoría de manuales viene en idioma inglés, aunque encontrará posibles traducciones o manuales actualizados en idioma español en Internet. Como actividad complementaria se sugiere que tome la referencia del dispositivo y busque su manual en Internet.
Para éste ejercicio, se propone identificar algunos botones de éste dispositivo:
a. Pulsadores multiplicadores de frecuencia:
En el panel frontal del dispositivo, se encuentra una serie de botones, entre ellos varios pulsadores, los cuales se activan presionando cada uno de ellos. Los pulsadores de enclavamiento, se identifican fácilmente pues sobre ellos hay una series de potencias de 10 en notación científica generalmente (x10; x100; x1K; x1M…), esto quiere decir que el número que aparece en el display, debe ser multiplicado por ésta escala.
Ladillo: Pulsador de enclavamiento es un botón que al ser pulsado queda en una posición (Hundido) y al presionarlo nuevamente, cambia de posición (Sobresale del panel).

112. b. La perilla de Spam:
La perilla de Spam, generalmente de forma cilíndrica, permite variar la frecuencia; para identificarlo, al encender el generador de señales y girar dicha perilla, cambia el numero que aparece en el display.
c. La perilla de amplitud:
Se debe observar que en cada perilla o botón, aparece un label o mensaje indicando su función, en éste caso la perilla de amplitud tiene en su parte superior la palabra “Amplitude”, al girar dicha perilla es modificada dicha característica de la señal de salida.
d. Conector BNC, y la sonda:
En el panel frontal, se encuentra una serie de conectores BNC, para cable coaxial. En la salida, se observa un mensaje “Output”, donde se conecta la sonda de salida, dicha sonda tiene en un extremo el conector que se ajusta al BNC, girándolo a la derecha luego de realizar la inserción, en su otro extremo, tiene los terminales de salida, uno para la señal y otro para tierra o referencia.
Existen dos clases de osciloscopios, los análogos y los digitales, éstos últimos han agregando una serie de funciones, hacienda más fácil su uso. En esta sección se explica el uso de uno osciloscopio análogo, en lo referente a las funciones necesarias para el estudio de los dispositivos que se tratan en esta sección.
Figura 7.2.1.2 Osciloscopio

113. Tomado de:
http://1.bp.blogspot.com/_aOBjZS-9nGA/SltxtmfJPwI/AAAAAAAAAHM/Lc4t0t8zi3M/s1600-h/2- Osciloscopio.jpg, [Cit. Dic - 29 de 2009].
Como se observa en el panel frontal, los botones y perillas esta agrupados en secciones según su función, la señal que es tomada desde la sonda, se visualiza en la pantalla que es un tubo de rayos catódicos, (algunos televisores que funcionaron bajo éste principio), se sugiere al estudiante, leer bibliografía o webgrafía que ilustre el funcionamiento de dicho dispositivo como una actividad complementaria.
Ladillo: Emulación, se refiere a la prueba que se hace en tiempo real sobre el dispositivo en condiciones ideales, buscando predecir el comportamiento de dicho dispositivo ante una situación específica.
RESUMEN
La asociación de condensadores, obedece a algoritmos de solución similares a las resistencias, pese a que su comportamiento es totalmente diferente, para efectos de aprendizaje, se puede decir que para resolver topologías en serie de condensadores, se usa el algoritmo de las resistencias en paralelo; para resolver condensadores en paralelo se usa el algoritmo de las resistencias en serie.
El uso de instrumentos como el generador de señales y el osciloscopio, es de gran importancia, sobre todo al analizar dispositivos electrónicos como el condensador, el cual presenta un comportamiento diferente a las señales directas (DC) o alternas (AC). Siempre se recomienda, para familiarizarse con el uso adecuado de cualquier instrumento, leer detenidamente el manual comprendiendo la función de cada una de sus partes y opciones de uso.

114. BIBLIOGRAFIA RECOMENDADA
INTERNET:
http://es.wikipedia.org/wiki/Condensador_el%C3%A9ctrico
http://www.configurarequipos.com/doc357.html
MULTIMEDIALES:
http://www.tu.tv/videos/carga-electrica-condensadores
http://www.tu.tv/videos-ext/43166008-campo-electrico-de-un-condensador
http://www.acienciasgalilei.com/videos/condensador.htm
http://www.youtube.com/watch?v=IG0MS7g9MJc
NEXO
El estudio del condensador permite profundizar en el estudio de dispositivos pasivos, los cuales mediante su configuración realizan funciones en diferentes tópicos y aplicaciones electrónicas, los condensadores también denominados filtros, pueden ser asociados o interconectados en circuitos con bobinas o semiconductores, para complementar o realizar una función, de las expuestas en la sección anterior.
El comportamiento de los condensadores es complementario al delas bobinas, pues los dos dispositivos actúan sobre la corriente y el voltaje, permitiendo realizar acciones de filtraje y se pueden tratar como factores resistivos, mediante las reactancias.
SEGUIMIENTO DE AUTOAPRENDIZAJE
1. En las siguientes gráficas, halla la capacitancia equivalente.
a. Todas las capacitancias son de C=300 μf.

115. C5
C1
C2
C3
C4
C7
C8
C9
C10
C11
C12
A
B
b. C1=100 μf; C2=300 μf y C3=150 μf
MODULO 8
8. BOBINAS
INTRODUCCION
Casi que se puede conseguir cualquier valor de resistencia o condensador en el mercado para las aplicaciones que se desean, pero con la bobinas no sucede lo mismo, en muchas ocasiones se hace necesario la construcción de éstas, pues no es sencillo obtener los valores deseados. En este capítulo, se estudia básicamente algunas generalidades de éstas y se plantea el cómo hallar la Inductancia equivalente, se expone como construir una bobina y las formulas que se usan para tal fin. Conceptos como Inductancia, aparecen en los circuitos eléctricos, cuando hay líneas de conducción.
MAPA CONCEPTUAL

116. LOGROS
 Reconocer las principales características de las bobinas y su equivalente en las configuraciones serie, paralelo y mixto.
 Determinar las variables a tener en cuenta en la construcción de una bobina y aplicarlas en ésta actividad.
 Identificar los principios físicos que explican el comportamiento eléctrico de una bobina.
8.1 PRINCIPIOS Y DEFINICIÓN
A diferencia del condensador / capacitor, que almacena energía en forma de campo eléctrico, la bobina por su forma (espiras de alambre arrollados) almacena energía en forma de campo magnético.

117. Todo cable por el que circula una corriente tiene a su alrededor un campo magnético, siendo el sentido de flujo del campo magnético, el que establece la ley de la mano derecha (ver electromagnetismo).
Al estar la bobina hecha de espiras de cable, el campo magnético circula por el centro de la bobina y cierra su camino por su parte exterior.
Una característica interesante de las bobinas es que se oponen a los cambios bruscos de la corriente que circula por ellas.
Esto significa que a la hora de modificar la corriente que circula por ellas (ejemplo: ser conectada y desconectada a una fuente de alimentación de corriente continua), esta intentará mantener su condición anterior.
La inductancia depende del material y la forma geométrica de la bobina, al igual que por la permeabilidad magnética del medio donde se encuentra. Según las ecuaciones propuestas por Maxwell, la ecuación de la inductancia viene dada por:
Ecuación 8.1.1
Dónde:
N = Número de espiras
A= Área de la sección transversal del bobinado.
L = Longitud de la bobina.
μ = Permeabilidad del vacío = 4π x 10-7 Wb.A-1.m-1 = 4π x 10-7 T.A-1.m
Las unidades de la Permeabilidad Magnética son: Webers sobre Amperios por metro o Teslas por metro sobre Amperios.
Actividad:

118. Construya una bobina con las siguientes características:
Área transversal: 2 cm
l= 3 cm
N = 20 espiras
μ = 1 para el aire.
8.2 CLASIFICACIÓN DE BOBINAS
Figura 8.2.1 Aspecto físico de algunas bobinas.
Tomado de: http://es.wikipedia.org/wiki/Archivo:Inductors-photo.JPG, [Cit. Dic. 29 de 2009]
Existe infinidad de fabricantes de bobinas, y se han hecho avances en la estandarización para la identificación de su medida, sin embargo, la mayoría de bobinas son fabricadas de manera empírica o artesanal. En la Figura 8.2.1, se observan algunas bobinas, la primera de izquierda a derecha, tiene en su carcaza, la medida de su inductancia. La unidad de medida para la inductancia es el Henrio o Henry (1 H), en honor a Joseph Henry (1797-1878).
Las inductancias, se clasifican según varios criterios, entre ellos se tiene:
A. Según su núcleo:
a. Núcleo de Aire: Se realiza un devanado, sobre un material no conductor o sobre el mismo material, según la firmeza de éste.

119. b. Núcleo de ferrita: Se usa un material ferro magnético, el cual tiene una alta permeabilidad, esto permite aumentar la inductancia de la bobina.
c. Núcleo de Hierro: Al tener mayor permeabilidad que el aire, permite aumentar la inductancia. Se usa en bajas frecuencias, pues a altas frecuencias, las pérdidas son muy altas.
B. Según las características de su valor
a. Fijas: Son inductancias o bobinas, con un valor fijo, el fabricante configura las variables, para garantizar dicho parámetro al comprador.
b. Variables: Son bobinas que tienen un cursor o elemento móvil que permite cambiar el valor de la inductancia.
Figura. 8.2.2 Simbología de las bobinas en los circuitos
Tomado de: http://www.mundoelectronica.netfirms.com/bobinas.htm [Op. Cit. 28 de Dic. de 2009]
8.3. CÓDIGOS
A continuación, se presenta algunas formas para identificar el valor de la inductancia de una bobina.
8.3.1. DETERMINACIÓN POR NOMENCLATURA
Muchas bobinas tienen impreso el valor de la inductancia en su carcaza como se mencionó en la sección 8.2. Otras tienen un código equivalente al código de

120. colores de las resistencias. El valor deducido por la configuración de los colores observados, se da en micro henrios (μH).
Tabla 8.3.1.1 código de colores
Color
1ª Cifra y 2ª Cifra
Multiplicador
Tolerancia
Negro
0
1
-
Marrón
1
10
-
Rojo
2
100
-
Naranja
3
1000
±3%
Amarillo
4
-
-
Verde
5
-
-
Azul
6
-
-
Violeta
7
-
-
Gris
8
-
-
Blanco
9
-
-
Oro
-
0,1
±5%
Plata
-
0,01
±10%
Ninguno
-
-
±20%
Ejemplo: Una bobina, tiene la siguiente configuración de colores:
Tabla 8.3.1.2 Ejemplo código de colores para Bobinas
1 cifra
2 cifra
3cifra (Multiplicador)
Tolerancia
Café
Negro
Rojo
Oro
1
0
2
±5%
Luego la lectura es: 10 X 102 = 1000 Micro Henrios (μH). La tolerancia se suma y se resta, luego la inductancia está entre 900 y 1100 micro Henrios (μH)
APRENDIZAJE COLABORATIVO
ACTIVIDAD: Escriba el valor de las siguientes inductancias, envíe sus resultados a uno de sus compañeros y compárelos. Proponga 10 ejercicios más y pídale a su compañero que haga lo mismo, resuélvanlos y comparen sus resultados, argumentando sus respuestas:

121. 1 Cifra
2 Cifra
Multiplicador
Tolerancia
Valor
Café
Negro
Amarillo
Plateado
Rojo
Café
Negro
Oro
Amarillo
Negro
Verde
Oro
Verde
Azul
Violeta
Plateado
Azul
Naranja
Rojo
Oro
8.3.2. DETERMINACIÓN POR INSTRUMENTO
Una forma alterna y efectiva en el laboratorio es el de usar un circuito RLC, (Resistencia, Condensador y Bobina), para que a partir de una señal de entrada tipo senosoidal y el osciloscopio, se determine el valor de la bobina, para ello se sigue el procedimiento que a continuación se expone:
a. Se implementa en el protoboard el circuito RLC, como se muestra en el plano. Con los valores de Resistencia y Condensador conocidos por el usuario.
Figura 8.3.2.1 Circuito para determinar Inductancias.
b. Se determina la frecuencia de resonancia: Después de hacer el montaje en el protoboard, se somete a una señal de entrada tipo senosoidal, haciendo un barrido en frecuencia, con el generador de señales, mediante el botón spam, el cual varía las frecuencias de salida en el rango seleccionado. cuando se note un cambio en la amplitud, entre un máximo y un mínimo, se detiene la exploración y se determina la frecuencia de resonancia.
1kHzV1-10/10VR11kL11uHC11uF1kHzV1-10VR11kL11uHC11uF

122. c. Determinación de la inductancia: Como la frecuencia de resonancia se da cuando la impedancia es igual para la inductancia y la capacitancia, se igualan las impedancias y se despeja la inductancia.
Para la reactancia capacitiva, según la ecuación 6.5.1 se tiene que:
Reactancia Inductiva:
Ecuación 8.3.2.1
Igualando las dos ecuaciones y despejando L se tiene que:
Ecuación 8.3.2.2
De esta ecuación se conoce la frecuencia y la capacitancia, por tanto solo es reemplazar en la fórmula y hallar L.
8.4. COMPORTAMIENTO EN AC Y DC
8.4.1 COMPORTAMIENTO EN DC
Cuando conectamos una bobina a una fuente DC, solamente se produce el efecto de la resistencia ofrecida por el alambre con que está fabricada, pero con una pequeña diferencia con respecto a un circuito puramente resistivo.
Cuando aplicamos el voltaje a un circuito resistivo, la corriente toma inmediatamente su valor máximo cuando se cierra el circuito. En cambio, en un

123. circuito inductivo (debido a que posee un inductor), la corriente se tarda un determinado tiempo para llegar al valor máximo.
A este tiempo se le llama constante de tiempo inductivo y depende de la inductancia en Henrios de la bobina y de su resistencia
8.4.2 COMPORTAMIENTO EN AC
Cuando aplicamos un voltaje de corriente alterna a una bobina, se producirá en ella un campo magnético que está variando continuamente. Por lo tanto, debido al fenómeno de la autoinducción, existirá también un voltaje contrario inducido permanentemente en oposición a la corriente alterna principal.
Esta oposición que ofrece una bobina a los voltajes de corriente alterna se llama reactancia inductiva. La reactancia inductiva se representa por las letras XL y se mide en Ohmios. La reactancia inductiva depende de la frecuencia de la señal o voltaje alterno y de la inductancia de la bobina, como aparece en la ecuación 8.3.2.1.
8.4.1. REACTANCIA INDUCTIVA
Es el efecto resistivo que tiene una bobina sobre un circuito y depende de la frecuencia angular, como en el caso del condensador, la unidad de medida también es el Ohmio, éste efecto está relacionado al igual que los condensadores con el concepto de fasor, el cual obedece a la componente real de éste. Cómo se mostró en la práctica relacionada con la determinación de la inductancia, ésta depende de la frecuencia y la inductancia. La ecuación que relaciona tales variables, se encuentra en la sección 8.3.
8.5. ASOCIACIÓN DE BOBINAS
Al igual que las resistencias, las bobinas tiene ecuaciones que permiten determinar una inductancia equivalente, las ecuaciones son semejantes a las de las resistencias. A continuación se explica cómo hallar en cada caso la Inductancia Equivalente.

124. 8.5.1. SERIE:
Las inductancias en serie se suman, tal como se hace con las resistencias, cabe aclarar que el valor obtenido es el de la Inductancia Equivalente en Henrios. En el ejemplo se muestra cómo se debe proceder en éste caso:
Ejemplo: Inductancias en serie.
Las bobinas en serie se suman, como se muestra en la ecuación:
Ecuación 8.5.1
En éste caso, la Inductancia total es:
8.5.2. PARALELO:
Las inductancia en paralelo, se tratan como las resistencias, en el ejemplo se muestra cómo proceder para hallar la Inductancia equivalente en paralelo.
Tal como la ecuación para resistencias, las bobinas o inductancias en paralelo están determinadas por:
Ecuación 8.5.2
En el ejemplo se muestra una forma de solución para esta topología.
Ejemplo: Halle la Inductancia equivalente del siguiente arreglo:
L41uHL310uHL2100uH

125. Aplicando la ecuación 8.5.2, se tiene que:
Como se observa el resultado esta dado por:
Se debe prestar mucha atención a las unidades para expresar los resultados.
8.5.3. MIXTO:
Como se indico en la sección de las resistencias, se pretende analizar la
configuración de éste circuito para deducir la fórmula que permite hallar la
inductancia equivalente, si se desarrolla esta habilidad no es necesario memorizar
las fórmulas, solo el procedimiento. En el ejemplo se muestra una alternativa para
solucionar éste tipo de topologías.
Ejemplo: Halle la inductancia equivalente del siguiente arreglo:
Para proceder, se empieza solucionando desde la salida, hasta la entrada, es
decir, desde L4 hasta L2. Inicialmente se soluciona el paralelo entre L4 y L3.
L4
1uH
L3
10uH
L2
100uH
L1
1uH
L4
1uH
L3
10uH
L2
100uH

126. El circuito se transforma en:
Como se observa, ahora las inductancias L1 y Leq1 quedan en serie, luego la Leq2
queda:
Finalmente se resuelve el paralelo entre L2 y Leq2, para hallar la inductancia total,
LT:
Se desarrollo el ejercicio de manera similar a como se hizo con las resistencias,
una vez más se hace énfasis en la necesidad de adquirir la habilidad de resolver
éste tipo de ejercicios, sin entrar a memorizar fórmulas que no son necesarias, es
relevante la forma como se desarrolla, pues de ella se desprende la comprensión
lógica del concepto.
8.6. EL TRANSFORMADOR
Una de las aplicaciones en electrónica es la de reducir el voltaje que llega de la
red de distribución eléctrica a nuestras casa, esto nos permite usar el voltaje en
niveles más apropiados pata los diferentes dispositivos electrónicos, los cuales
funcionan con voltaje DC, en los niveles de 5V por ejemplo para circuitos
lógicos. Para tal fin se diseñan unos dispositivos electrónicos llamados fuentes
L1
1uH
Leq1
0.90uH
L2
100uH
Leq2
1.90uH
L2
100uH

127. de voltaje, estas permiten convertir dicho voltaje con las características que se señalan anteriormente.
El componente central que permite una primera reducción es el transformador, el cual reduce el voltaje de 110 V a una relación de voltaje, específica según el fabricante. Cabe aclarar que no solo se usan a 110V, es posible encontrar transformadores con niveles de voltaje y relaciones de transformación en una amplia gama, según las necesidades, en éste caso se estudia el transformador como reductor de voltaje.
8.6.1. PRINCIPIO DE FUNCIONAMIENTO
Anteriormente se expuso la necesidad de reducir el voltaje, para usarlo en aplicaciones donde se requiere tal condición. La aparición del transformador se hace necesaria en sus principios, gracias a la necesidad de transmisión de energía eléctrica, donde se debe usar elevados voltajes a corrientes bajas, reduciendo la cantidad de calor en la línea de transmisión.
Un transformador está conformado por dos bobinas aisladas eléctricamente y arrolladas sobre el mismo núcleo de hierro. Un voltaje alterno entra por una de las bobinas, identificadas como primario del transformador, ésta genera un flujo variable generando un campo eléctrico inducido, hacia la otra bobina, denominada secundario. De esta manera se transmite energía de una bobina a la otra.
Figura 8.6.1.1 Símbolo del transformador.
El símbolo de un transformador con núcleo de hierro se presenta en la Figura 8.6.1.1. Como se observa existen 2 bobinados uno primario por sonde entra el potencial aplicado AC y el secundario por donde es inducido el voltaje o potencial.
T110TO1

128. En su funcionamiento existen pérdidas, denominadas pérdidas por Histéresis y por torbellino, las dos son contra restadas por el uso de hierro con un ciclo de histéresis estrecho y las corrientes se reducen con un núcleo laminado.
En este caso se considera un transformador ideal donde no se presentan perdidas, en el bobinado primario hay un número de vueltas superior al secundario. La corriente de entrada al primario se denomina magnetizante, el flujo del primario está en fase con la corriente primaria, el voltaje inducido es igual en ambos, luego la razón entre los voltajes y el número de espiras en los devanados está dada por la ecuación: Ecuación 8.6.1.1
Escogiendo la relación entre los voltajes y el numero de espiras en cada devanado, se tiene que: si V2 > V1 se tiene un transformador elevador, pero si V2 < V1 el transformador se comporta como un reductor.
La potencia suministrada al primario es la misma que se extrae del secundario, por tanto:
Ecuación 8.6.1.2
De donde al combinar las ecuaciones 8.6.1.1. y 8.6.1.2, se tiene que:
Ecuación 8.6.1.3

129. Esto se tiene cuando se conecta una resistencia en el secundario, como se puede observar en la ecuación, el transformador no solo transforma corrientes y voltajes sino también resistencias. En el siguiente ejemplo se muestra cómo usar estas ecuaciones para diseñar un transformador.
Ejemplo: Se requiere que el voltaje en el primario sea de 110 V y en el secundario sea de 25 V. La corriente de entrada al primario es de 4 A. ¿Cuál es la corriente en el devanado primario, si la resistencia de salida es de 1KΩ?
Para resolver éste problema, se debe tener en cuenta que el transformador es de tipo reductor. Se hace uso de las ecuaciones 8.6.1.1 y 8.6.1.3, de donde se tiene que:
Luego la relación entre los devanados debe ser de 4, es decir, todas las fracciones equivalentes a 4 son aplicables a dicho parámetro de diseño. Se puede usar la misma que parece entre los voltajes, es decir en el secundario 25 vueltas y en el primario 110. Ahora, aplicando la ecuación 8.6.1.3, se tiene que:
La corriente en el primario es de 0,5 A. con una relación de potencia igual, se puede deducir la corriente en el secundario:
Luego I2 = 2,2 A, es obvio que dicha corriente depende de la resistencia que se conecte en el secundario, sin embargo como conclusión se puede determinar que la inducción hace que la corriente necesaria en el secundario, dependa de la corriente en el primario y que en el proceso de inducción se producen pérdidas.

130. RESUMEN
Las bobinas son componentes cuyas características en AC y DC, son complementarias a los condensadores. La reactancia Inductiva es una muestra de ello. Las bobinas tienen una amplia gama de aplicaciones, desde los circuitos osciladores hasta los filtros, en el campo de las comunicaciones principalmente. En éste capítulo, solo se trato el tema desde la asociación e bobinas en las topologías serie, paralelo y mixto, los cuales se pueden deducir a partir de las ecuaciones usadas para las resistencias en dichas topologías.
Una aplicación de las inductancias, es el transformador, el cuál en muchas de los diseños en electrónica se usa para reducir los niveles de voltaje, de gran utilidad en el momento de diseñar fuentes de voltaje, que convierten niveles de voltaje AC a voltaje DC.
BIBLIOGRAFIA RECOMENDADA
INTERNET:
http://www.configurarequipos.com/doc357.html
MULTIMEDIALES:
http://www.tu.tv/videos/carga-electrica-condensadores
http://www.tu.tv/videos-ext/43166008-campo-electrico-de-un-condensador
http://www.acienciasgalilei.com/videos/condensador.htm
TEXTOS:
ROBBINS, Allan. Análisis de circuitos Teoría y práctica. Introducción. Cengace Learning. 2007. p. 3 - 21.

131. A B
L5
1uH
L4
1uH
L3
1uH
L1
1uH
L2
1uH
L1
1uH
A L5 B
150uH
L4
150uH
L3
0.25uH
L1
0.5uH
L2
0.25uH
L1
0.5uH
KAUFFMAN, Milton. Electrónica Práctica y Moderna. Capítulo 3. Mc Graw-
Hill. 1998.
NEXO
Los conceptos vistos en éste capítulo, se observarán en cursos posteriores de
análisis de circuitos, así como en el caso de circuitos sintonizados, como el caso
de filtros pasivos y osciladores, los cuales son la base fundamental en la
transmisión de señales, como por ejemplo en Frecuencia Modulada (FM) y
Amplitud Modulada (AM). De igual manera las bobinas son usadas en aplicaciones
industriales como el modelamiento de arrancadores para motores en delta –
estrella y viceversa.
Los transformadores son dispositivos de un amplia gama de aplicaciones, entre
las que se encuentra la reducción y elevación de voltaje, mediante la inducción
magnética, aunque la fabricación de éstos depende de muchas variables, aún es
una actividad muy rentable, y práctica. En el diseño de circuitos electrónicos en
muchas ocasiones, se requiere del uso de dicho dispositivo, de ahí la importancia
de comprender a cabalidad dicho concepto.
SEGUIMIENTO DE AUTOAPRENDIZAJE
1. En los siguientes arreglos, determine la inductancia total.
a.
b.

132. L1
1uH
R1
100k
C1
0.001uF
1kHz
V1
-15/15V
2. Halle la reactancia inductivas, si se requiere que sea igual a la resistencia
del circuito que se muestra a continuación y la frecuencia de resonancia.
(Use la Ecuación 8.3.2.2)
a.
3. Se requiere que la relación entre el voltaje de entrada del transformador sea
de 110V a 20 V, con una corriente en el secundario de 4 A. ¿Cuál debe ser
la relación entre los devanados y la resistencia que se debe colocar en el
secundario para tal fin?