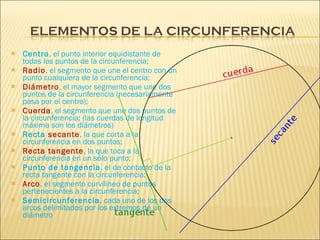
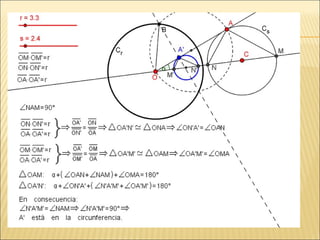
El documento describe las características básicas de las circunferencias. Define una circunferencia como el conjunto de puntos equidistantes de un centro, y distingue entre circunferencia (perímetro) y círculo (área interior). Explica conceptos como radio, diámetro y cuerda, y cómo representar circunferencias mediante ecuaciones cartesianas, polares y en un plano oblicuo.
Circunferencias tangentes a circunferencia y a recta,dado el punto de tangenc...Antonio García
Problema clásico de tangencias el de circunferencias tangentes a recta y a circunferencia dado el punto de tangencia en la recta, con la dificultad añadida de que este punto está en el interior de la circunferencia.
Circunferencias tangentes exteriores a una recta y a una circunferencia, pasa...Antonio García
Hemos de resolver el caso de circunferencias que pasando por un punto o lugar determinado, son tangentes a dos elementos propuestos cuales son una recta y una circunferencia. Para resolver este problema clásico que se atribuye a Apolonio de Perga, hemos de echar mano de los conocimientos adquiridos sobre transformaciones geométricas, como son la inversión y la potencia de un punto respecto de una circunferencia, y que aquí ejercen un papel prerponderante.
Circunferencias tangentes a circunferencias pasando por un punto P.Antonio García
En esta ocasión hay que resolver el problema de hacer pasar las circunferencias por un punto dado y que sean tangentes a las propuestas. Para ello empleamos los conceptos de inversión y potencia de un punto respecto de una circunferencia. Este par de soluciones que aquí se entregan están halladas por inversión negativa, es decir situando el centro de inversión entre los dos puntos inversos, los centros de las circunferencias propuestas. Ni que decir tiene que existen otro par de soluciones que se resuelven por inversión positiva.
TANGENCIAS, ENLACES Y RECTIFICACIONES. Dibujo Técnico IJUAN DIAZ ALMAGRO
Documento que muestra teoría y ejercicios resueltos de TANGENCIAS, ENLACES Y RECTIFICACIONES DE LA CIRCUNFERENCIA. Está diseñado para el Dibujo Técnico de 1º de bachillerato, aunque se seguirá utilizando también en 2º.
Circunferencias tangentes a circunferencia y a recta,dado el punto de tangenc...Antonio García
Problema clásico de tangencias el de circunferencias tangentes a recta y a circunferencia dado el punto de tangencia en la recta, con la dificultad añadida de que este punto está en el interior de la circunferencia.
Circunferencias tangentes exteriores a una recta y a una circunferencia, pasa...Antonio García
Hemos de resolver el caso de circunferencias que pasando por un punto o lugar determinado, son tangentes a dos elementos propuestos cuales son una recta y una circunferencia. Para resolver este problema clásico que se atribuye a Apolonio de Perga, hemos de echar mano de los conocimientos adquiridos sobre transformaciones geométricas, como son la inversión y la potencia de un punto respecto de una circunferencia, y que aquí ejercen un papel prerponderante.
Circunferencias tangentes a circunferencias pasando por un punto P.Antonio García
En esta ocasión hay que resolver el problema de hacer pasar las circunferencias por un punto dado y que sean tangentes a las propuestas. Para ello empleamos los conceptos de inversión y potencia de un punto respecto de una circunferencia. Este par de soluciones que aquí se entregan están halladas por inversión negativa, es decir situando el centro de inversión entre los dos puntos inversos, los centros de las circunferencias propuestas. Ni que decir tiene que existen otro par de soluciones que se resuelven por inversión positiva.
TANGENCIAS, ENLACES Y RECTIFICACIONES. Dibujo Técnico IJUAN DIAZ ALMAGRO
Documento que muestra teoría y ejercicios resueltos de TANGENCIAS, ENLACES Y RECTIFICACIONES DE LA CIRCUNFERENCIA. Está diseñado para el Dibujo Técnico de 1º de bachillerato, aunque se seguirá utilizando también en 2º.
ROMPECABEZAS DE ECUACIONES DE PRIMER GRADO OLIMPIADA DE PARÍS 2024. Por JAVIE...JAVIER SOLIS NOYOLA
El Mtro. JAVIER SOLIS NOYOLA crea y desarrolla el “ROMPECABEZAS DE ECUACIONES DE 1ER. GRADO OLIMPIADA DE PARÍS 2024”. Esta actividad de aprendizaje propone retos de cálculo algebraico mediante ecuaciones de 1er. grado, y viso-espacialidad, lo cual dará la oportunidad de formar un rompecabezas. La intención didáctica de esta actividad de aprendizaje es, promover los pensamientos lógicos (convergente) y creativo (divergente o lateral), mediante modelos mentales de: atención, memoria, imaginación, percepción (Geométrica y conceptual), perspicacia, inferencia, viso-espacialidad. Esta actividad de aprendizaje es de enfoques lúdico y transversal, ya que integra diversas áreas del conocimiento, entre ellas: matemático, artístico, lenguaje, historia, y las neurociencias.
Instrucciones del procedimiento para la oferta y la gestión conjunta del proceso de admisión a los centros públicos de primer ciclo de educación infantil de Pamplona para el curso 2024-2025.
![[object Object],[object Object],[object Object],[object Object]](data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7)