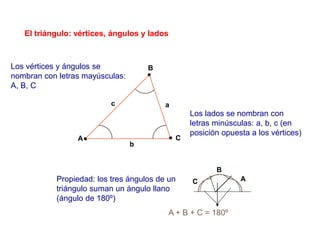
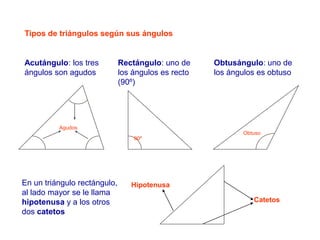
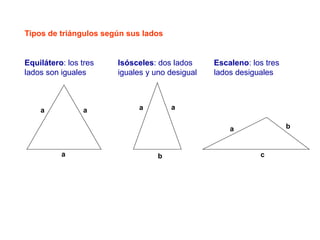
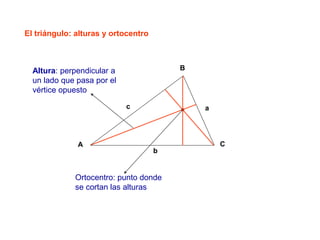
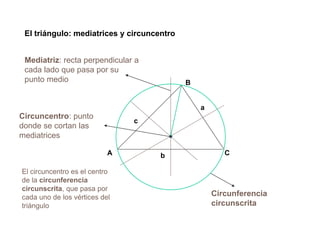
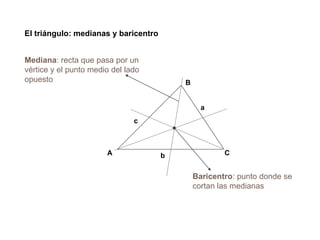
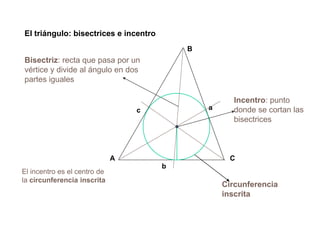
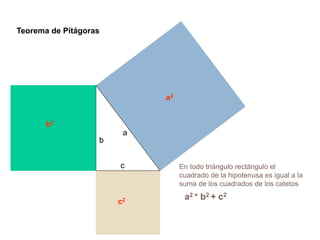
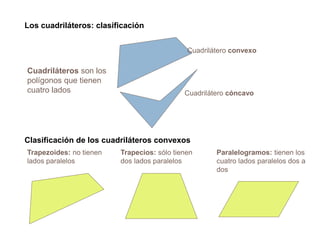
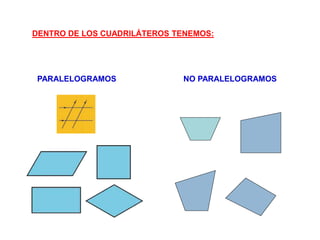
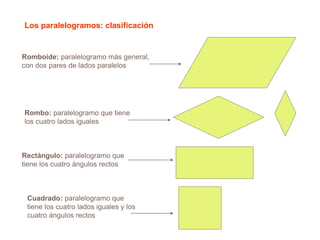
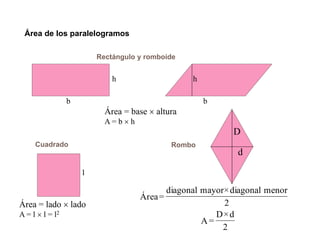
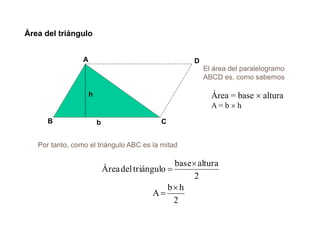
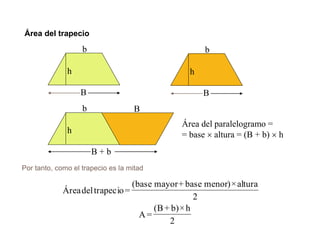
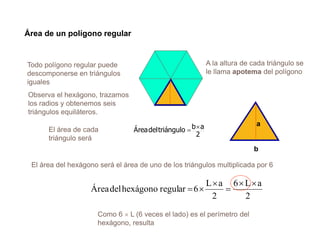
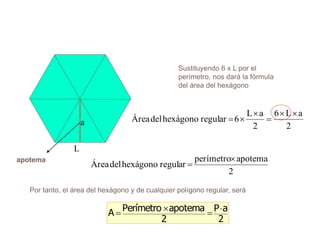
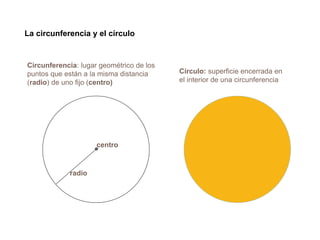
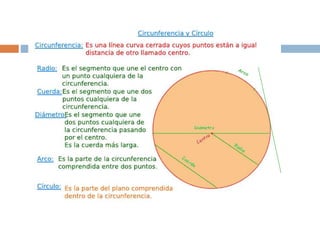
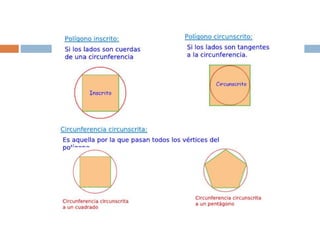
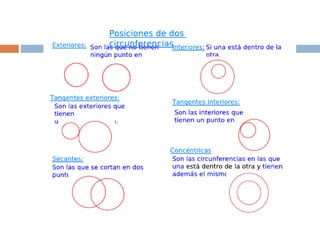
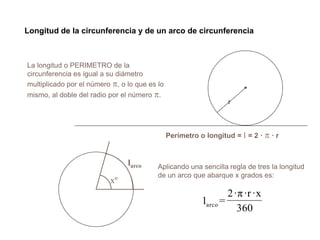
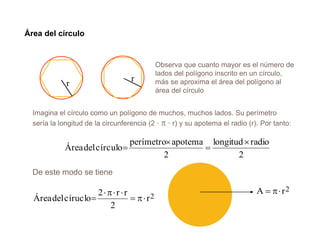
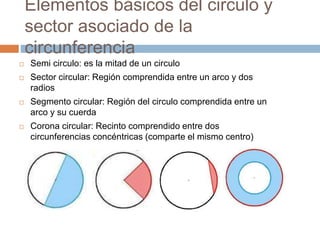
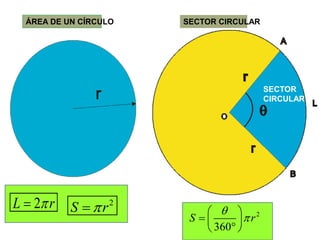
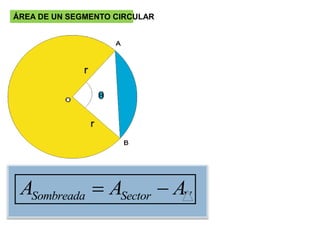
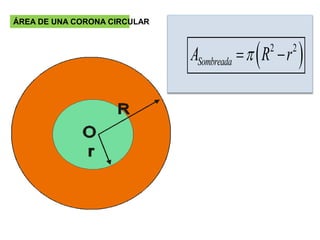
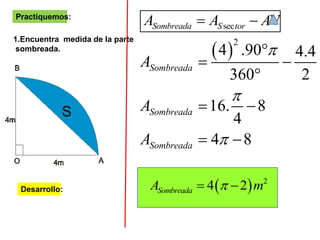
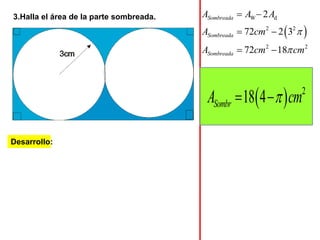
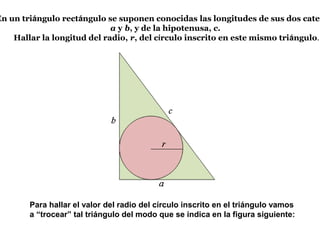
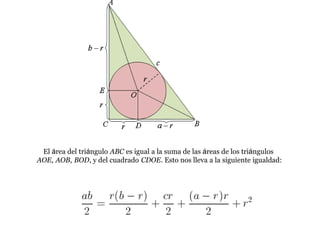
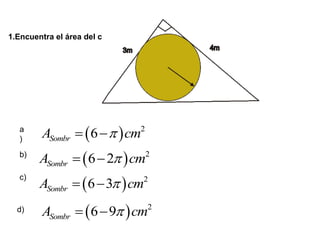
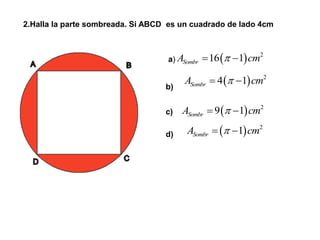
El documento presenta información sobre los conceptos básicos de triángulos, cuadriláteros, círculos y sectores circulares. Explica las propiedades y fórmulas para calcular el área de estas figuras geométricas, incluyendo triángulos, paralelogramos, trapecios, círculos y sectores circulares. También cubre conceptos como vértices, ángulos, lados, clasificación de triángulos y cuadriláteros, y elementos del círculo como radio, diámetro, circunferencia

1. ÁREA Y PERÍMETRO DE
UN CIRCULO Y
SECTORES ASOCIADOS
A LA CIRCUNFERENCIA
Miss Yanira Castro Lizana

2. C
El triángulo: vértices, ángulos y lados
Propiedad: los tres ángulos de un
triángulo suman un ángulo llano
(ángulo de 180º)
Los vértices y ángulos se
nombran con letras mayúsculas:
A, B, C
Los lados se nombran con
letras minúsculas: a, b, c (en
posición opuesta a los vértices)
A + B + C = 180º
A
B
a
b
c
A
B
C

3. Tipos de triángulos según sus ángulos
Acutángulo: los tres
ángulos son agudos
Rectángulo: uno de
los ángulos es recto
(90º)
Obtusángulo: uno de
los ángulos es obtuso
Agudos
Obtuso
90º
En un triángulo rectángulo,
al lado mayor se le llama
hipotenusa y a los otros
dos catetos
Catetos
Hipotenusa

4. Tipos de triángulos según sus lados
Equilátero: los tres
lados son iguales
Isósceles: dos lados
iguales y uno desigual
Escaleno: los tres
lados desiguales
a a
a
a a
b
a b
c

5. A
B
C
a
b
c
El triángulo: alturas y ortocentro
Ortocentro: punto donde
se cortan las alturas
Altura: perpendicular a
un lado que pasa por el
vértice opuesto

6. CA
B
a
b
c
El triángulo: mediatrices y circuncentro
Circuncentro: punto
donde se cortan las
mediatrices
Mediatriz: recta perpendicular a
cada lado que pasa por su
punto medio
El circuncentro es el centro
de la circunferencia
circunscrita, que pasa por
cada uno de los vértices del
triángulo
Circunferencia
circunscrita

7. CA
B
a
b
c
El triángulo: medianas y baricentro
Baricentro: punto donde se
cortan las medianas
Mediana: recta que pasa por un
vértice y el punto medio del lado
opuesto

8. El triángulo: bisectrices e incentro
Incentro: punto
donde se cortan las
bisectrices
Bisectriz: recta que pasa por un
vértice y divide al ángulo en dos
partes iguales
El incentro es el centro de
la circunferencia inscrita
CA
B
a
b
c
Circunferencia
inscrita

9. Teorema de Pitágoras
En todo triángulo rectángulo el
cuadrado de la hipotenusa es igual a la
suma de los cuadrados de los catetos
a
b
c
a2 = b2 + c2
a2
b2
c2

10. Los cuadriláteros: clasificación
Cuadriláteros son los
polígonos que tienen
cuatro lados
Cuadrilátero convexo
Cuadrilátero cóncavo
Clasificación de los cuadriláteros convexos
Trapezoides: no tienen
lados paralelos
Trapecios: sólo tienen
dos lados paralelos
Paralelogramos: tienen los
cuatro lados paralelos dos a
dos

11. DENTRO DE LOS CUADRILÁTEROS TENEMOS:
PARALELOGRAMOS NO PARALELOGRAMOS

12. Los paralelogramos: clasificación
Romboide: paralelogramo más general,
con dos pares de lados paralelos
Rombo: paralelogramo que tiene
los cuatro lados iguales
Rectángulo: paralelogramo que
tiene los cuatro ángulos rectos
Cuadrado: paralelogramo que
tiene los cuatro lados iguales y los
cuatro ángulos rectos

13. Área de los paralelogramos
Rectángulo y romboide
h
b
Área = base  altura
A = b  h
l
Cuadrado
Área = lado  lado
A = l  l = l2
Rombo
D
d
2
d×D
=A
2
menordiagonal×mayordiagonal
=Área
b
h

14. Área del triángulo
DA
B Cb
h
El área del paralelogramo
ABCD es, como sabemos
Área = base  altura
A = b  h
Por tanto, como el triángulo ABC es la mitad
2
hb
A
2
alturabase
triángulodelÁrea





15. Área del trapecio
b
B
h
b
B
h
b
h
B
B + b
Área del paralelogramo =
= base  altura = (B + b)  h
2
h×)b+B(
=A
2
altura×)menorbase+mayorbase(
=trapeciodelÁrea
Por tanto, como el trapecio es la mitad

16. Área de un polígono regular
Todo polígono regular puede
descomponerse en triángulos
iguales
Como 6  L (6 veces el lado) es el perímetro del
hexágono, resulta
El área del hexágono será el área de uno de los triángulos multiplicada por 6
A la altura de cada triángulo se
le llama apotema del polígono
2
aL6
2
aL
6regularhexágonodelÁrea




Observa el hexágono, trazamos
los radios y obtenemos seis
triángulos equiláteros.
2
abtriángulodelÁrea El área de cada
triángulo será
b
a

17. Sustituyendo 6 x L por el
perímetro, nos dará la fórmula
del área del hexágono
L
a
apotema
2
aL6
2
aL
6regularhexágonodelÁrea




2
apotemaperímetro
regularhexágonodelÁrea


Por tanto, el área del hexágono y de cualquier polígono regular, será
2
aP
2
apotemaPerímetroA 

18. La circunferencia y el círculo
Circunferencia: lugar geométrico de los
puntos que están a la misma distancia
(radio) de uno fijo (centro)
Círculo: superficie encerrada en
el interior de una circunferencia
centro
radio

22. Longitud de la circunferencia y de un arco de circunferencia
La longitud o PERIMETRO de la
circunferencia es igual a su diámetro
multiplicado por el número , o lo que es lo
mismo, al doble del radio por el número .
r
Perímetro o longitud = l = 2 ·  · r
Aplicando una sencilla regla de tres la longitud
de un arco que abarque x grados es:
360
x·r·π·2
=larco
larco
xº

23. Área del círculo
Observa que cuanto mayor es el número de
lados del polígono inscrito en un círculo,
más se aproxima el área del polígono al
área del círculo
r
r
Imagina el círculo como un polígono de muchos, muchos lados. Su perímetro
sería la longitud de la circunferencia (2 ·  · r) y su apotema el radio (r). Por tanto:
2
radiolongitud
2
apotemaperímetro
círculodelÁrea




2r
2
rr2
círuclodelÁrea 


De este modo se tiene
2rA 

24. Elementos básicos del circulo y
sector asociado de la
circunferencia
 Semi circulo: es la mitad de un circulo
 Sector circular: Región comprendida entre un arco y dos
radios
 Segmento circular: Región del circulo comprendida entre un
arco y su cuerda
 Corona circular: Recinto comprendido entre dos
circunferencias concéntricas (comparte el mismo centro)

25. ÁREA DE UN CÍRCULO SECTOR CIRCULAR
2L r 2
S r 2
360
S r


 
  
 
SECTOR
CIRCULAR

26. ÁREA DE UN SEGMENTO CIRCULAR
Sombreada SectorA A A  V

27. ÁREA DE UNA CORONA CIRCULAR
 2 2
SombreadaA R r 

28. Practiquemos:
1.Encuentra medida de la parte
sombreada.
Desarrollo:
secSombreada S torA A A  V
 
2
4 .90 4.4
360 2
16. 8
4
4 8
Sombreada
Sombreada
Sombreada
A
A
A




 

 
 
  2
4 2SombreadaA m 

29. 2.Encuentra la parte sombreada:
Desarrollo:
2 2
6 3
36 9
Sombreada
Sombreada
Sombreada
A A A
A
A


 
 
 
W d
  2
9 4SombreadaA cm 

30. 3.Halla el área de la parte sombreada.
Desarrollo:
  2
18 4SombrA cm 
 2 2
2 2
2
72 2 3
72 18
Sombreada
Sombreada
Sombreada
A A A
A cm
A cm cm


 
 
 
W d

31. En un triángulo rectángulo se suponen conocidas las longitudes de sus dos catet
a y b, y de la hipotenusa, c.
Hallar la longitud del radio, r, del círculo inscrito en este mismo triángulo.
Para hallar el valor del radio del círculo inscrito en el triángulo vamos
a “trocear” tal triángulo del modo que se indica en la figura siguiente:

32. El área del triángulo ABC es igual a la suma de las áreas de los triángulos
AOE, AOB, BOD, y del cuadrado CDOE. Esto nos lleva a la siguiente igualdad:

33. Eliminando denominadores y paréntesis se tiene:
Igualdad esta última de la que se deduce que el valor del radio es:

34. 1.Encuentra el área del círculo
a
)
b)
c)
d)
  2
6SombrA cm 
  2
6 2SombrA cm 
  2
6 3SombrA cm 
  2
6 9SombrA cm 

35. 2.Halla la parte sombreada. Si ABCD es un cuadrado de lado 4cm
a)
b)
c)
d)
  2
16 1SombrA cm 
  2
4 1SombrA cm 
  2
9 1SombrA cm 
  2
1SombrA cm 