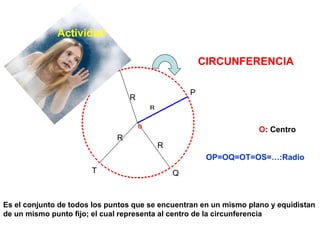
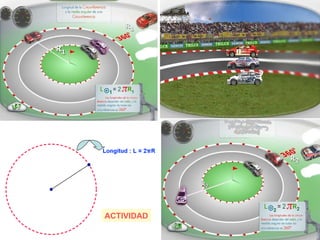
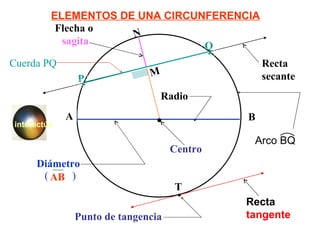
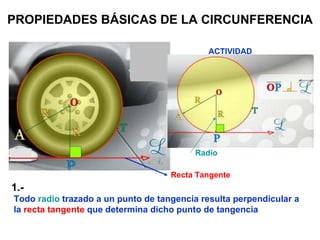
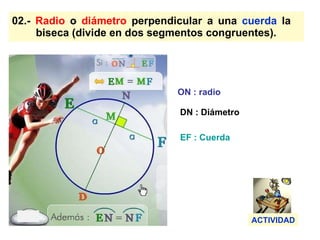
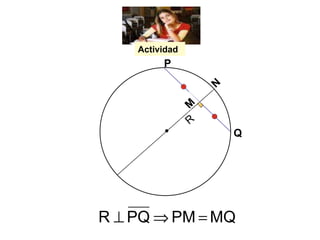
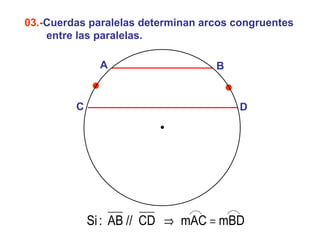
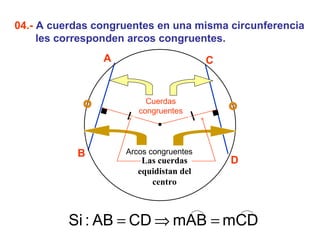
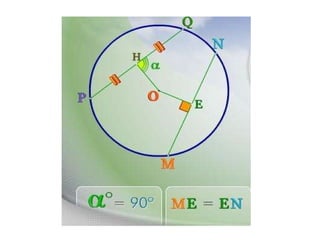
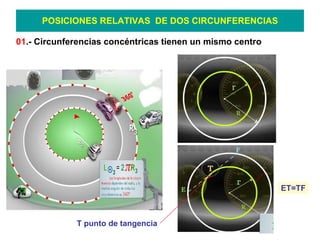
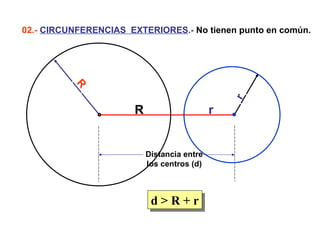
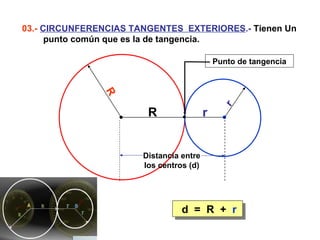
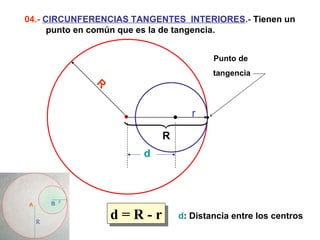
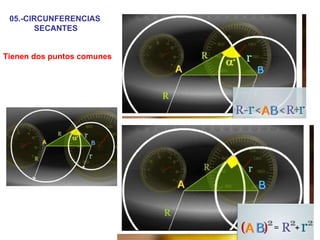
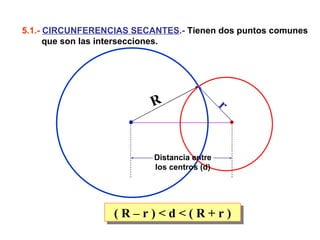
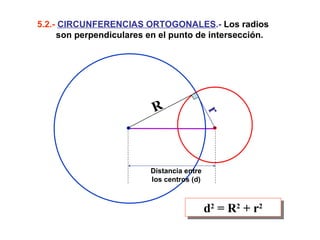
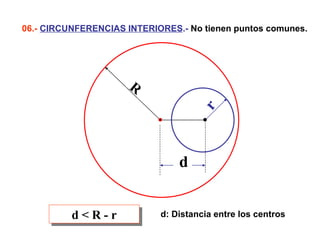
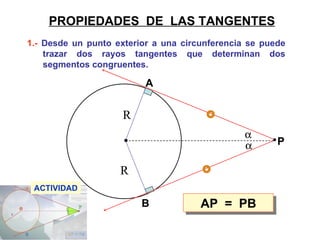
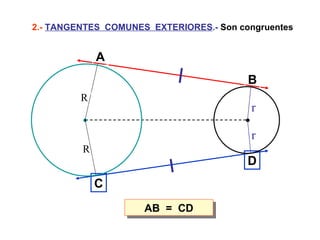
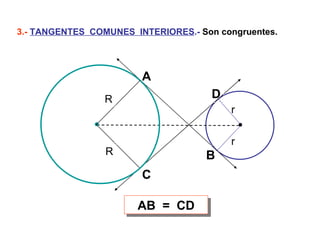
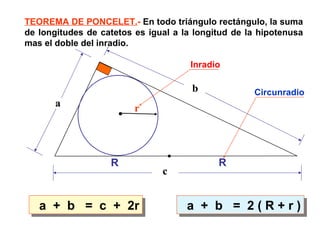
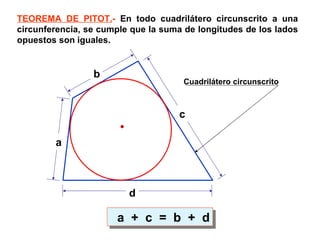
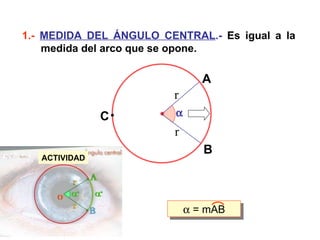
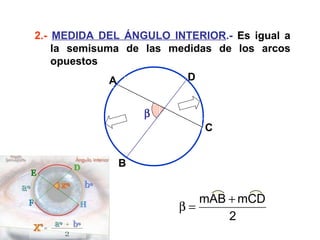
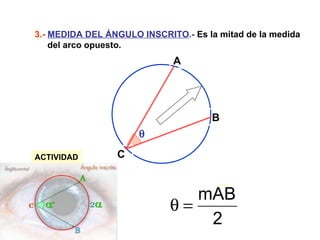
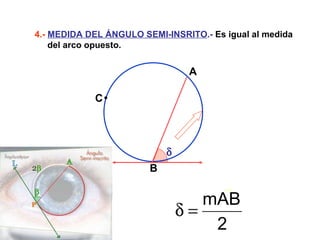
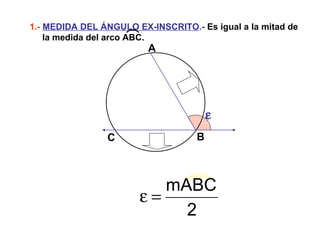
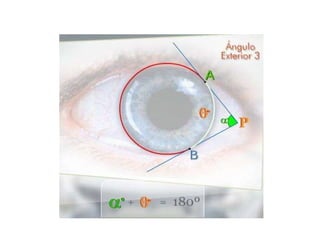
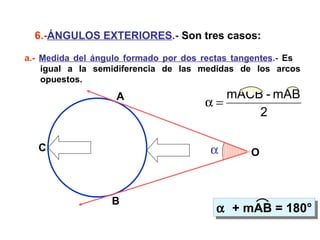
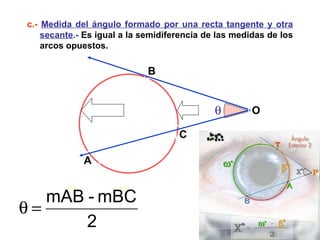
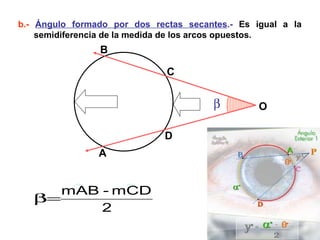
Este documento describe las propiedades geométricas de las circunferencias y ángulos relacionados. Define una circunferencia como el conjunto de puntos equidistantes de un centro, e identifica sus elementos como radio, diámetro, arco, cuerda y puntos de tangencia. Explica las posiciones relativas de dos circunferencias como concéntricas, exteriores, tangentes o secantes. También cubre teoremas como la suma de catetos igual a la hipotenusa más el doble del inradio.

1. LA CIRCUNFERENCIA R

2. ¿Qué figuras tienen la forma de círculo y circunferencia?

3. Es el conjunto de todos los puntos que se encuentran en un mismo plano y equidistan de un mismo punto fijo; el cual representa al centro de la circunferencia P Q T S R R R O : Centro OP=OQ=OT=OS=…:Radio CIRCUNFERENCIA Actividad

4. ACTIVIDAD

5. ELEMENTOS DE UNA CIRCUNFERENCIA  interactúa A B M N Recta tangente Recta secante Flecha o sagita Diámetro AB ( ) Centro T  Punto de tangencia Q  P  Radio Arco BQ Cuerda PQ

6. PROPIEDADES BÁSICAS DE LA CIRCUNFERENCIA Todo radio trazado a un punto de tangencia resulta perpendicular a la recta tangente que determina dicho punto de tangencia Recta Tangente Radio 1.- ACTIVIDAD

7. 02.- Radio o diámetro perpendicular a una cuerda la biseca (divide en dos segmentos congruentes). ON : radio DN : Diámetro EF : Cuerda ACTIVIDAD

8. Actividad P Q M N R

9. 03.- Cuerdas paralelas determinan arcos congruentes entre las paralelas. A B C D

10. 04.- A cuerdas congruentes en una misma circunferencia les corresponden arcos congruentes. A B C D Cuerdas congruentes Arcos congruentes Las cuerdas equidistan del centro

12. POSICIONES RELATIVAS DE DOS CIRCUNFERENCIAS 01 .- Circunferencias concéntricas tienen un mismo centro T punto de tangencia ET=TF

13. 02.- CIRCUNFERENCIAS EXTERIORES .- No tienen punto en común. d > R + r R r Distancia entre los centros (d) R r

14. d = R + r 03.- CIRCUNFERENCIAS TANGENTES EXTERIORES .- Tienen Un punto común que es la de tangencia. r R R r Punto de tangencia Distancia entre los centros (d)

15. d = R - r 04.- CIRCUNFERENCIAS TANGENTES INTERIORES .- Tienen un punto en común que es la de tangencia. d : Distancia entre los centros d R R r Punto de tangencia

16. 05.-CIRCUNFERENCIAS SECANTES Tienen dos puntos comunes

17. 5.1.- CIRCUNFERENCIAS SECANTES .- Tienen dos puntos comunes que son las intersecciones. ( R – r ) < d < ( R + r ) R r Distancia entre los centros (d)

18. 5.2.- CIRCUNFERENCIAS ORTOGONALES .- Los radios son perpendiculares en el punto de intersección. d 2 = R 2 + r 2 Distancia entre los centros (d) r R

19. 06.- CIRCUNFERENCIAS INTERIORES .- No tienen puntos comunes. d < R - r d: Distancia entre los centros R r d

20. 1.- Desde un punto exterior a una circunferencia se puede trazar dos rayos tangentes que determinan dos segmentos congruentes. PROPIEDADES DE LAS TANGENTES AP = PB ACTIVIDAD A B P R R  

21. 2.- TANGENTES COMUNES EXTERIORES .- Son congruentes AB = CD A B C D R R r r

22. 3.- TANGENTES COMUNES INTERIORES .- Son congruentes. AB = CD A B C D R R r r

23. TEOREMA DE PONCELET. - En todo triángulo rectángulo, la suma de longitudes de catetos es igual a la longitud de la hipotenusa mas el doble del inradio. a + b = c + 2r a + b = 2 ( R + r ) a b c r R R Inradio Circunradio

24. TEOREMA DE PITOT. - En todo cuadrilátero circunscrito a una circunferencia, se cumple que la suma de longitudes de los lados opuestos son iguales. a + c = b + d d a b c Cuadrilátero circunscrito

25. II.-ÁNGULOS EN LA CIRCUNFERENCIA

26. 1.- MEDIDA DEL ÁNGULO CENTRAL .- Es igual a la medida del arco que se opone. ACTIVIDAD  A B C r r  = mAB

27. 2.- MEDIDA DEL ÁNGULO INTERIOR .- Es igual a la semisuma de las medidas de los arcos opuestos  A C B D

28. 3.- MEDIDA DEL ÁNGULO INSCRITO .- Es la mitad de la medida del arco opuesto. ACTIVIDAD  A B C

29. 4.- MEDIDA DEL ÁNGULO SEMI-INSRITO .- Es igual al medida del arco opuesto.  A B C

30.  A B C 1.- MEDIDA DEL ÁNGULO EX-INSCRITO .- Es igual a la mitad de la medida del arco ABC.

32. 6.- ÁNGULOS EXTERIORES .- Son tres casos: a.- Medida del ángulo formado por dos rectas tangentes .- Es igual a la semidiferencia de las medidas de los arcos opuestos.  A B C O  + mAB = 180°

33. c.- Medida del ángulo formado por una recta tangente y otra secante .- Es igual a la semidiferencia de las medidas de los arcos opuestos.  A B C O

34. b.- Ángulo formado por dos rectas secantes .- Es igual a la semidiferencia de la medida de los arcos opuestos.  A B C O D