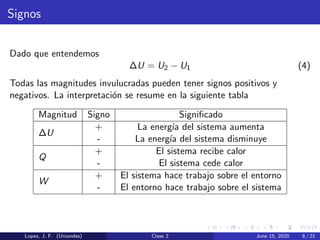
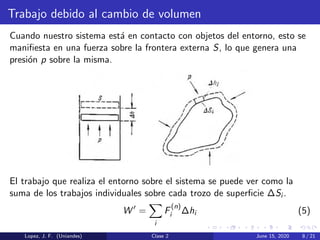
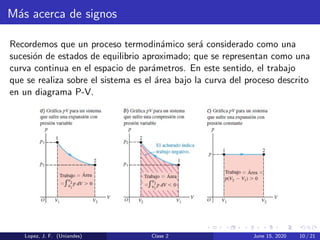
Este documento presenta la primera ley de la termodinámica y diferentes procesos termodinámicos. Explica conceptos como la energía interna de un sistema, el trabajo realizado por un cambio de volumen, y la relación entre el cambio de energía interna, el calor transferido y el trabajo. También describe procesos como isocórico, isobárico e isotérmico, y aplica los conceptos a un ejemplo numérico.

1. Primera ley y procesos termodin´amicos
Juan Felipe L´opez
Universidad de los Andes – Uniandes
June 15, 2020
Lopez, J. F. (Uniandes) Clase 2 June 15, 2020 1 / 21

2. Contents
1 Energ´ıa interna y primera ley
2 Trabajo debido al cambio de volumen
Lopez, J. F. (Uniandes) Clase 2 June 15, 2020 2 / 21

3. Contents
1 Energ´ıa interna y primera ley
2 Trabajo debido al cambio de volumen
Lopez, J. F. (Uniandes) Clase 2 June 15, 2020 3 / 21

4. Energ´ıa Interna
Llamaremos energ´ıa interna de un sistema, usando la letra U, a la energ´ıa
de todas las componentes del cuerpo, eliminando la eneg´ıa cin´etica del
cuerpo como un todo (i.e. centro de masa y rotaci´on total) y la energ´ıa
potencial del cuerpo como un todo. Es decir, la energ´ıa cin´etica de las
mol´eculas, la energ´ıa potencial de interacci´on e intramolecular.
T´ıpicamente la interacci´on del sistema con el medio es despreciable.
La energ´ıa interna es una funci´on de estado.
Lopez, J. F. (Uniandes) Clase 2 June 15, 2020 4 / 21

5. Primera Ley
Del curso de F´ısica I, aprendimmos que por el Teorema del Trabajo y la
Energ´ıa, la energ´ıa mec´anica puede variar por el trabajo de una fuerza. Por
otro lado, aprendimos en la sesi´on pasada que se puede utilizar el calor
suministrado a un cuerpo para realizar un trabajo. La conservaci´on de la
energ´ıa toma entonces la forma
∆U = Q + W (1)
Donde ∆U es el cambio en la energ´ıa interna, Q es el calor transmitido al
sistema y W es el trabajo que el entorno realiza sobre el sistema. Si
queremos s´olo informaci´on medida por el sistema, podemos considerar el
trabajo que el sistema realiza sobre el entorno W , que por Tercera ley de
Newton
W = −W (2)
La primera ley toma la forma m´as conocida
Q = ∆U + W (3)
Lopez, J. F. (Uniandes) Clase 2 June 15, 2020 5 / 21

6. Signos
Dado que entendemos
∆U = U2 − U1 (4)
Todas las magnitudes invulucradas pueden tener signos positivos y
negativos. La interpretaci´on se resume en la siguiente tabla
Magnitud Signo Significado
∆U
+ La energ´ıa del sistema aumenta
- La energ´ıa del sistema disminuye
Q
+ El sistema recibe calor
- El sistema cede calor
W
+ El sistema hace trabajo sobre el entorno
- El entorno hace trabajo sobre el sistema
Lopez, J. F. (Uniandes) Clase 2 June 15, 2020 6 / 21

7. Contents
1 Energ´ıa interna y primera ley
2 Trabajo debido al cambio de volumen
Lopez, J. F. (Uniandes) Clase 2 June 15, 2020 7 / 21

8. Trabajo debido al cambio de volumen
Cuando nuestro sistema est´a en contacto con objetos del entorno, esto se
manifiesta en una fuerza sobre la frontera externa S, lo que genera una
presi´on p sobre la misma.
El trabajo que realiza el entorno sobre el sistema se puede ver como la
suma de los trabajos individuales sobre cada trozo de superficie ∆Si .
W =
i
F
(n)
i ∆hi (5)
Lopez, J. F. (Uniandes) Clase 2 June 15, 2020 8 / 21

9. Trabajo debido al cambio de volumen
Donde F
(n)
i es la fuerza que act´ua sobre ∆Si normal a la superficie.
Recordemos
Presi´on
Se define como la fuerza por unidad de ´area normal a la superficie.
Adem´as, si el sistema est´a en equilibrio, la presi´on es constante sobre toda
la superficie
F
(n)
i = p∆Si ,
pero i ∆Si ∆hi es s´olo el cambio en el volumen ∆V . Convirtiendo la
suma en una integral, y pasando a la perspectiva del sistema
W = −
V2
V1
pdV (6)
Lopez, J. F. (Uniandes) Clase 2 June 15, 2020 9 / 21

10. M´as acerca de signos
Recordemos que un proceso termodin´amico ser´a considerado como una
sucesi´on de estados de equilibrio aproximado; que se representan como una
curva continua en el espacio de par´ametros. En este sentido, el trabajo
que se realiza sobre el sistema es el ´area bajo la curva del proceso descrito
en un diagrama P-V.
Lopez, J. F. (Uniandes) Clase 2 June 15, 2020 10 / 21

11. Tipos de procesos
Proceso isoc´orico
Es un proceso que ocurre a volumen constante. El trabajo realizado por
este proceso es nulo.
Proceso isob´arico
Es un proceso que ocurre a presi´on constante constante.
W = p dV = p∆V = p(V2 − V1) (7)
Proceso isot´ermico
Es un proceso que ocurre a temperatura constante constante constante. El
trabajo depende de la ecuaci´on de estado.
Lopez, J. F. (Uniandes) Clase 2 June 15, 2020 11 / 21

12. Expansi´on isot´ermica del gas ideal
A temperatura constante, la presi´on de un gas ideal en funci´on del
volumen es
p(V ) = nRT
1
V
(8)
Y el trabajo
W =
V2
V1
p(V )dV = nRT
V2
V1
dV
V
= nRT ln
V2
V1
(9)
A temperatura constante
p1V1 = p2V2;
V2
V1
=
p1
p2
(10)
Entonces
W = nRT ln
p1
p2
(11)
Lopez, J. F. (Uniandes) Clase 2 June 15, 2020 12 / 21

13. Tipos de procesos
Proceso adiab´atico
Es un proceso en el que no hay intercambio de calor (Q = 0). En este
caso, W = −∆U.
Proceso c´clico
Es un proceso tal que el punto de inicio y el punto final son iguales.
Determina una curva cerrada en el diagrama de par´ametros. W = Q.
Lopez, J. F. (Uniandes) Clase 2 June 15, 2020 13 / 21

14. Ejemplo
Considere un 1mol gas ideal con presi´on y volumen iniciales (p0, V0).
Realiza una expansi´on a presi´on constante hasta duplicar su volumen
inicial. Luego, realiza una compresi´on a temperatura constante de forma
que al final del proceso, la presi´on es el triple de la presi´on inicial. Luego,
se enfr´ıa mediante un proceso isoc´orico hasta alcanzar su temperatura
inicial. Describa la presi´on, volumen y temperatura en cada punto en que
terminan los subprocesos; y el trabajo realizado.
Soluci´on
Lopez, J. F. (Uniandes) Clase 2 June 15, 2020 14 / 21

15. Ejemplo
Lopez, J. F. (Uniandes) Clase 2 June 15, 2020 15 / 21

16. Ejemplo
Tenemos en el estado (0), volumen y presi´on V0, p0, y temperatura
T0 =
p0V0
R
(12)
Donde est´e escrito R se entiende que es (1mol)R. En el estado (1), como
el proceso es isob´arico p1 = p0 y V1 = 2V0
T1 =
p1V1
R
= 2
p0V0
R
(13)
En (2), p2 = 3p0 y
T2 = T1 = 2
p0V0
R
, V2 =
RT2
p2
=
2
3
V0 (14)
En (3)
V3 = V2 =
2
3
V0, T3 = T0 =
p0V0
R
, p3 =
RT3
V3
=
3
2
p0 (15)
Lopez, J. F. (Uniandes) Clase 2 June 15, 2020 16 / 21

17. Ejemplo
El proceso de (0) a (1) es isob´arico
W 1
0 = p0(V1 − V0) = p0(2V0 − V0) = p0V0 (16)
El proceso de (1) a (2) es isot´ermico
W 2
1 = RT1 ln
p1
p2
= 2p0V0 ln
p0
3p0
= −2ln(3)p0V0 (17)
El proceso de (2) a (3) es isoc´orico
W 3
2 = 0 (18)
El trabajo total del proceso (0, 1, 2, 3)
WT = −(2ln(3) − 1)p0V0 (19)
Lopez, J. F. (Uniandes) Clase 2 June 15, 2020 17 / 21

18. Relaciones diferenciales
Si consideramos un proceso infinitesimal cuasiest´atico, podemos reescibir
la primera ley en las siguientes notaciones
dU = d Q − d W = d Q − pdV = δQ − δW (20)
Donde la notaci´on dU indica un cambio deferencial en la variable de estado
Energ´ıa Interna. La notaci´on d W o δW hace referencia a un elemento
diferencial de trabajo. No escribimos dW , dado que no existe una funci´on
de estado Trabajo. El trabajo no se asocia al estado termodin´amico sino al
proceso. Diferentes procesos que van entre el mismo par de estados
realizan distintos trabajos. Lo mismo sucede con el calor.
Caratheodory formaliz´o las leyes de la termodin´amica en el lenguaje de la
geometr´ıa diferencial. Lo anterior se refiere de forma t´ecnica a que dU es
un diferencial exacto mientras que d W y d Q no lo son.
Lopez, J. F. (Uniandes) Clase 2 June 15, 2020 18 / 21

19. Referencias I
F.W. Sears.
FISICA UNIVERSITARIA.
Number v. 1 in F´ısica universitaria. Pearson Educaci´on, 2013.
Sav´eliev I. V.
Curso de F´ısica General 1. Mecanica F´ısica molecular.
Mosc´u, mir edition, 1984.
M. Alonso and E.J. Finn.
Fisica - Volumen 3 Fundamentos Cuanticos y Estadis.
Number v. 3 in F´ısica. Addison-Wesley Iberoamericana, 1992.
R.A. Serway and J.W. Jewett.
Fisica Para Ciencias E Ingenieria, Volumen 2.
F´ısica para ciencias e ingenier´ıa. Cengage Learning Editores S.A. de
C.V., 2014.
Lopez, J. F. (Uniandes) Clase 2 June 15, 2020 19 / 21

20. Referencias II
T. Frankel.
The Geometry of Physics: An Introduction.
Cambridge University Press, 2011.
Lopez, J. F. (Uniandes) Clase 2 June 15, 2020 20 / 21

21. Primera ley y procesos termodin´amicos
Juan Felipe L´opez
Universidad de los Andes – Uniandes
June 15, 2020
Lopez, J. F. (Uniandes) Clase 2 June 15, 2020 21 / 21