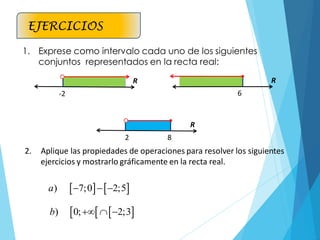
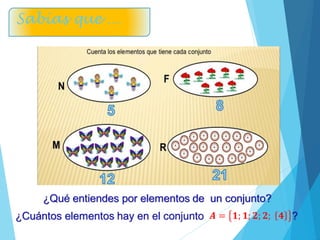
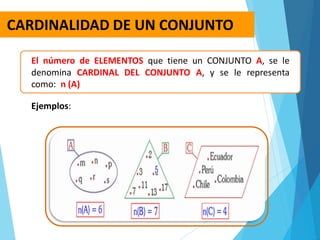
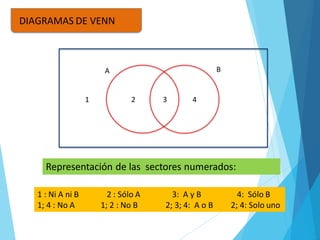
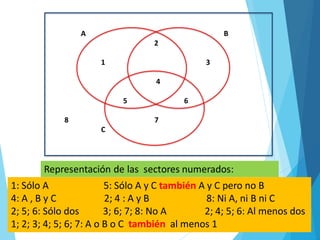
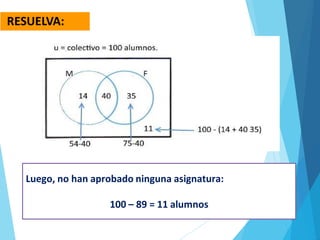
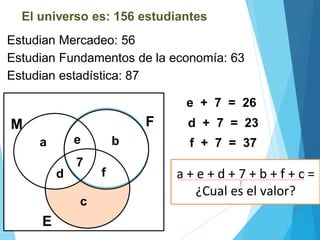
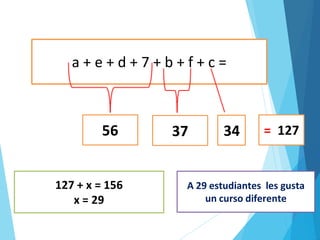
El documento aborda la cardinalidad de conjuntos y operaciones con intervalos, enfocándose en ejercicios prácticos para estudiantes de matemáticas. Incluye ejemplos de aplicaciones de conjuntos y la representación de intervalos en la recta numérica. Se ofrecen problemas para resolver y se sugiere un trabajo domiciliario en grupo con reflexiones sobre el aprendizaje.

1. CARDINALIDAD DE UN
CONJUNTO
Intervalos y operaciones con intervalos. Aplicaciones.
ASIGNATURA: MATEMÁTICA I

2. ¿Cuántos elementos hay en el conjunto ?
¿Qué entiendes por elementos de un conjunto?
Sabías que …
𝑨 = 𝟏; 𝟏; 𝟐; 𝟐; 𝟒

3. Sabías que …

4. Al finalizar la sesión, el
estudiante resuelve
ejercicios y problemas
sobre cardinalidad de
conjuntos e intervalos,
en situaciones de la vida
diaria, de manera
correcta.
LOGRO DE APRENDIZAJE

5. El número de ELEMENTOS que tiene un CONJUNTO A, se le
denomina CARDINAL DEL CONJUNTO A, y se le representa
como: n (A)
CARDINALIDAD DE UN CONJUNTO
Ejemplos:

6. A B
1 2 3 4
Representación de las sectores numerados:
1 : Ni A ni B 2 : Sólo A 3: A y B 4: Sólo B
1; 4 : No A 1; 2 : No B 2; 3; 4: A o B 2; 4: Solo uno
DIAGRAMAS DE VENN

7. A B
2
1 3
4
5 6
8 7
C
1: Sólo A 5: Sólo A y C también A y C pero no B
4: A , B y C 2; 4 : A y B 8: Ni A, ni B ni C
2; 5; 6: Sólo dos 3; 6; 7; 8: No A 2; 4; 5; 6: Al menos dos
1; 2; 3; 4; 5; 6; 7: A o B o C también al menos 1

8. RESUELVA:

9. RESUELVA:

10. 1. A un examen han concurrido 100 alumnos a rendir en
Matemáticas y Física. Sabiendo que las Matemáticas la
han aprobado 54 alumnos en total, la física 75 alumnos
en total y el número de alumnos que han aprobado
ambas asignaturas han sido 40.
Hallar la cantidad de alumnos que no han aprobado
ninguna asignatura.
RESUELVA:

11. Luego, no han aprobado ninguna asignatura:
100 – 89 = 11 alumnos
RESUELVA:

12. 2. En una investigación realizada a un grupo de 100
personas, que estudiaban varios idiomas fueron los
siguientes: Español 28, Alemán 30, Francés 42, Español
y Alemán 8, Español y Francés 10, Alemán y Francés 5 y
los tres idiomas 3.
a) ¿Cuántos alumnos no estudiaban idiomas?
b) ¿Cuántos alumnos tenían como francés el único idioma
de estudio?por los tres cursos mencionados?
RESUELVA:

13. RESUELVA:

14. 3. En la tercera semana de clase se hizo una encuesta a
156 estudiantes de 1er ciclo, acerca de sus cursos
favoritos. A 56 estudiantes de ellos les gusta el curso de
mercadeo, a 63 le gusta Fundamentos de economía, a
87 le gusta el curso de estadística. Además algunos de
ellos coinciden en que les gusta mas de un curso. A 26
de ellos les gusta el curso de mercadeo y Fundamentos
de economía. A 37 les gusta el curso de Fundamentos
de economía y estadística y a 23 estudiantes les gusta
mercadeo y estadística; por último 7 estudiantes
manifestaron su gusto por los tres cursos.
¿A cuántos estudiantes les gusta un curso diferente a los
antes mencionados?
RESUELVA:

15. El universo es: 156 estudiantes
Estudian Fundamentos de la economía: 63
Estudian estadística: 87
M F
E
a
d
e + 7 = 26
b
e
7
f
d + 7 = 23
c
Estudian Mercadeo: 56
f + 7 = 37
a + e + d + 7 + b + f + c =
¿Cual es el valor?

16. a + e + d + 7 + b + f + c =
56 37 34
127 + x = 156
x = 29
= 127
A 29 estudiantes les gusta
un curso diferente

17. INTERVALO
Los intervalos son subconjuntos de los números reales que se
pueden representar gráficamente en la recta numérica por un
trazo o una semirrecta.
a

b

 
[ ]
a

b


[ [
a

b


[ )
5. INTERVALO REAL

18. Desigualdad Notación Gráfica
a < x <b
[ a ; b ]
x 
[ a ; b [
x 
] a ; b ]
x 
] a ; b[
x 
a

b

 
a

b

a

b

a

b



   
Nota ; ; ;
a b a b a b
 
a  x  b
a  x < b
a < x b

REPRESENTACIÓN DE INTERVALOS

19. Desigualdad Notación Gráfica
[ a ; [
x 
]-  ; a]
x 
a

a

a

a


a ; [
x ]
]-  ; a[
x 

a
x 
a
x 
a
x <
a
x 
REPRESENTACIÓN DE INTERVALOS

20. OPERACIONES CON INTERVALOS
𝑨 ∪ 𝑩 Unión de A con B. Contiene todos los
elementos de A más todos los elementos de B.
𝐴 ∪ 𝐵 = {𝑥 ∈ ℝ / 𝑥 𝜖 𝐴 ó 𝑥 𝜖 𝐵}
-4 -3 2 3
Ejemplo:
A=[-4;2[ y B=[-3;3[. Calcular 𝐴 ∪ 𝐵
𝐴 ∪ 𝐵 = [−4;3[
𝐴 ∪ 𝐵
UNIÓN DE INTERVALOS

21. OPERACIONES CON INTERVALOS
𝑨 ∩ 𝑩 Intersección de A con B. Contiene todos los
elementos que son comunes a A y a B.
𝐴 ∩ 𝐵 = {𝑥 ∈ 𝑅 / 𝑥 𝜖 𝐴 𝑦 𝑥 𝜖 𝐵}
-4 -3 2 3
Ejemplo:
A=[-4;2[ y B=[-3;3[. Calcular 𝐴 ∩ 𝐵
𝐴 ∩ 𝐵 = [−3;2[
𝐴 ∩ 𝐵
INTERSECCIÓN DE INTERVALOS

22. OPERACIONES CON INTERVALOS
𝑨 − 𝑩 Diferencia A menos B. Contiene todos los
elementos que están en A, pero que no se encuentran
en B.
𝐴 − 𝐵 = {𝑥 ∈ ℝ / 𝑥 𝜖 𝐴 𝑦 𝑥 ∉ 𝐵}
-4 -3 2 3
Ejemplo:
A=[-4;2[ y B=[-3;3[. Calcular 𝐴 − 𝐵
𝐴 − 𝐵 = [−4;−3[
𝐴 − 𝐵
DIFERENCIA DE INTERVALOS
Nota: 𝐀 − 𝐁 ≠ 𝑩 − 𝑨

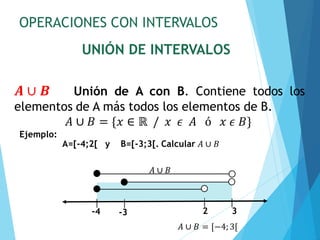
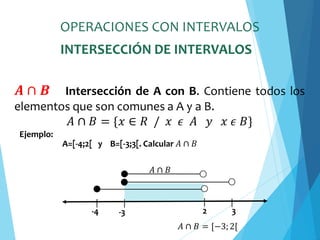
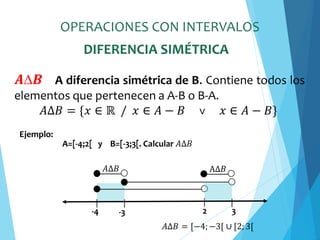
23. OPERACIONES CON INTERVALOS
𝑨´ Complemento de A. Contiene todos los elementos
que no se encuentran en A. También puede definirse
como ℝ-A.
𝐴′ = {𝑥 ∈ ℝ / 𝑥 ∉ 𝐴}
-4 2
Ejemplo:
A=[-4;2[ Calcular 𝐴′
𝐴 ∩ 𝐵 = ] − ∞;−4[ ∪ [2;+∞[
𝐴′ 𝐴′
COMPLEMENTO DE INTERVALOS

24. OPERACIONES CON INTERVALOS
𝑨𝑩 A diferencia simétrica de B. Contiene todos los
elementos que pertenecen a A-B o B-A.
𝐴∆𝐵 = {𝑥 ∈ ℝ / 𝑥 ∈ 𝐴 − 𝐵 ˅ 𝑥 ∈ 𝐴 − 𝐵}
Ejemplo:
DIFERENCIA SIMÉTRICA
A=[-4;2[ y B=[-3;3[. Calcular 𝐴∆𝐵
-4 -3 2 3
𝐴∆𝐵 = [−4;−3[ ∪ [2;3[
𝐴∆𝐵 A∆𝐵

25. OPERACIONES CON LOS EXTREMOS
DE LOS INTERVALOS
Fuente:
http://guillermoquinonesdiaz.blogspot.pe/2014/05/operaciones-con-intervalos-reunion.html

26. EJEMPLO
Escribe en la forma de desigualdad los siguientes enunciados:
a) La venta de artículos de una empresa no
excede a las 2000 unidades.
b) El ingreso obtenido por la venta de libros
de matemática I es mayor a las 10 000
unidades.
Resolución
Sea x el número de artículos, entonces.
Resolución
Sea I el ingreso dado , entonces:

27. 1. Exprese como intervalo cada uno de los siguientes
conjuntos representados en la recta real:
-2
R
6
R
2 8
R
2. Aplique las propiedades de operaciones para resolver los siguientes
ejercicios y mostrarlo gráficamente en la recta real.
   
) 7;0 2;5
a   
   
) 0; 2;3
b   
EJERCICIOS

28. Trabajo domiciliario (120 minutos)
Formamos grupos de 4 o 5 para la realización de las actividades.
1. Desarrollar los problemas propuestos en la Sesión 03 Práctica.
2. Desarrollar los problemas propuestos en la Práctica 03.
3. Todos los problemas serán presentados en la siguiente reunión y
expuestos.
Material adicional
PRÁCTICA EN EQUIPOS
Enlace 1
http://traful.utem.cl/portal/doc/capsulas-de-aprendizaje/capsula-tecnicas-
de-conteo/assets/material_descargable/ED_tecsdeconteo.pdf
Enlace 2
https://sites.google.com/site/matematicaseib2013/3-5-1-ejercicios-resueltos

29. 1. ¿Qué aprendí hoy?
2. ¿Qué dificultades he tenido?
3. ¿Cómo lo superé?
REFLEXIÓN
4. ¿ En qué situaciones de nuestra
vida se puede emplear
cardinalidad de conjuntos?

30. 1. Espinoza, E. (2012). Matemática Básica. 5ta .Edic. Lima.
2. Farfán, O. (2005). Aritmética. Lima: Edit. San Marcos.
3. Figueroa, R. (2006). Matemática Básica I. Lima: Ediciones
RFG.
4. Gamarra, H. (2007). Aritmética. Lima: Edit. San Marcos
E.I.R.L.
5. Lázaro, M. (2015). Matemática Básica. Lima: Moshera
S.R.L.
6. Venero, A. (2006). Matemática Básica. Lima: Ediciones
Gemar.
7. https://slideplayer.es/slide/13310977/
BIBLIOGRAFÍA