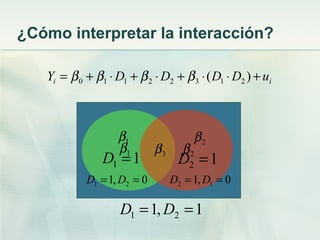
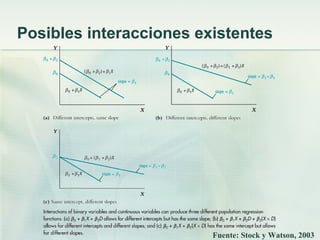
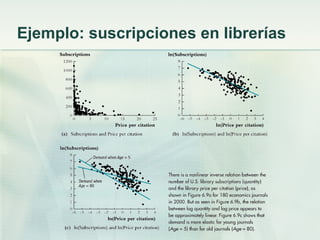
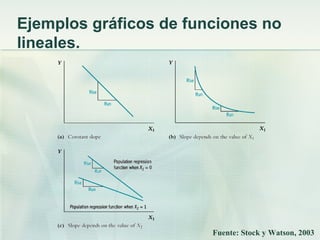
Este documento discute los modelos de regresión no lineales. Explica que los efectos marginales no son siempre constantes y que las relaciones entre variables pueden no ser lineales. Presenta dos métodos para modelar estimaciones no lineales: cuando el efecto de una variable depende de su propio valor o del valor de otra variable. Luego describe cómo especificar funciones polinómicas, de logaritmos y con interacciones entre variables para capturar relaciones no lineales.

1. Modelo de regresión múltiple
Estimación de modelos no lineales.
Sesión 8
11/marzo/2007

2. Ampliación del modelo OLS
 ¿Son los efectos marginales constantes a
medida que estas cambian?
 ¿La pendiente de la curva de producción es
constante a mayor cantidad de trabajadores?
 ¿Los el incremento marginal del rendimiento
financiero es el mismo cuando incrementa el
riesgo?
 ¿La respuesta del consumo ante un cambio
en el precio es igual para los hombres que
para las mujeres?
 Las estimaciones no lineales liberan estas
restricciones.

3. Dos métodos para detectar y
modelar estimaciones no lineales.
 Grupo 1: el efecto sobre Yi de un cambio en Xi depende del valor
de que tenga Xi.
 Ejemplo: Tamaño de clases y rendimiento de los alumnos.
 Grupo 2: el efecto sobre Yi de un cambio en Xi depende del valor
de que tenga algún otro Xi.
 Ejemplo: tipo de clases que se está llevando.
02
2
≠
∂
∂
X
Y
0
21
2
≠
∂∂
∂
XX
Y

4. Ejemplos gráficos de funciones no
lineales.
Fuente: Stock y Watson, 2003

5. Aproximación general a modelos no
lineales
1. Identificar una posible relación no lineal.
 Utilizar la teoría econométrica para invocar
aproximaciones no lineales
2. Especificar una función no lineal utilizando
parámetros OLS.
 Es necesario realizar transformaciones a la variable
Xi y/o Y.
3) Determinar si una función no lineal es superior
a una lineal.
 Buscar evidencia empírica que refleje esta
situación.

6. Aproximación general a modelos no
lineales
4) Graficar los valores no lineales de la función.
 En la medida de lo posible, graficar los valores
permite ver el grado de ajuste de la regresión.
4) Estimar el efecto en Y de un cambio en X.
 Tomar en cuenta que a diferencia de las
estimaciones lineales estos procesos requieren una
mayor complejidad.

7. Grupo 1
La pendiente de X depende de su valor.

8. Caso1: Polinomios
 Es un tipo de regresión múltiple donde un grupo de
variables independientes que corresponden a un mismo
Xi están elevados a un grado distinto de uno.
 Se describe como un polinomio grado r, donde r es la
mayor potencia del modelo estimado.
r
ki XXXY 1
2
12110 ... ⋅++⋅+⋅+= ββββ
Grado del
polinomio

9. Polinomios: ¿Qué grado usar?
1. Escoger un r máximo para comenzar:
 Mientras la serie es más suave el grado
inicial a testear debe ser bajo (4,3 o 2).
2. Encontrar el mejor modelo econométrico:
 Realizar testeo de pruebas de hipótesis.
 Comenzar con el máximo grado y testear si la
potencia mayor es significativa.
 Si no fuera significativa, realizar la prueba con un
grado menor.
 Utilizar criterios de información.

10. Polinomios y sus efectos marginales
01
ˆˆ YYY −=∆
r
k
r
k XXXXXXXXXY )(...)()()(...)()( 1
2
12111
2
1211 ⋅++⋅+⋅−∆+⋅++∆+⋅+∆+⋅=∆ ββββββ
r
kii XXXXXXYYY )(...)()(ˆ 1
2
12110 ∆+⋅++∆+⋅+∆+⋅+=∆+= ββββ
Estimación incluye el
cambio en xi
Estimación de Y con los
valores originales de xi
Notas sobre los efectos marginales:
 El valor explicativo de los coeficientes βk es más profundo en estimaciones
no lineales.
Requiere de mayor trabajo para conocer estimaciones puntuales.

11. Caso 2: Logaritmos
 Ventajas de los logaritmos:
 Convierte los cambios en las variables en cambios porcentuales.
 Logaritmos contienen propiedades deseables
 Utilizar logaritmos naturales (para materia de simplicidad, dará lo
mismo hablar de logaritmos naturales –ln- que logaritmos –log-)
x
x
xxx
∆
≅−∆+ )log()log(
)log()log(
)log()log()/log(
)log()log()log(
)log()/1log(
xax
xaxa
xaxa
xx
a
⋅=
−=
+=⋅
−=
)log()1()log()log()log( 1
ZXAZXA ⋅−+⋅+=⋅ −
ββββ

12. Linear – Log Model
 Logaritmos, caso 1:
 X está expresada en logaritmos, Y no lo está.
 El coeficiente β se interpreta como el efecto marginal
de δ cambio porcentual de xi.
iii uxY +⋅+= )log(10 ββ
[ ]
[ ]



∆
⋅≅∆
−∆+⋅=∆
+−∆++=∆
x
x
Y
xxxY
xxxY
1
1
1010
)log()log(
)log()log(
β
β
ββββ
Este término es una razón expresada en un
intervalo definido entre cero y uno.

13. Log – Linear Model
 Logaritmos, caso 2:
 Y está expresada en logaritmos, X no lo está.
 El coeficiente β se puede interpretar como el cambio
porcentual de xi.
iii uXY +⋅+= 10)log( ββ
Este término es una razón
expresada en un intervalo
definido entre cero y uno.
[ ]
x
Y
Y
xY
xxxY
∆⋅=
∆
∆⋅=∆
⋅+−∆+⋅+=∆
1
1
1010
)log(
)()log(
β
β
ββββ

14. Log - log Model (doble log)
 Logaritmos, caso 3:
 Y & X están expresada en logaritmos.
 El coeficiente β representa la elasticidad de Y
respecto a X.
iii uXY +⋅+= )log()log( 10 ββ
[ ]
[ ]
Y
x
x
Y
x
x
Y
Y
xxxY
xxxY
⋅
∆
∆
=
∆
⋅=
∆
−∆+⋅=∆
⋅+−∆+⋅+=∆
1
1
1
1010
)log()log()log(
)log()log()log(
β
β
β
ββββ

15. Grupo 2
La pendiente de X1 depende del valor de X2

16. Caso 1: interacción entre dos
variables dummy
 Considerando el caso básico de una variable
dummy:
 Limitación: el efecto de D1 sobre Y es el mismo
independientemente del valor de D2.
 Para liberar esta restricción se introduce un
tercer término:
ii uDDY +⋅+⋅+= 22110 βββ
ii uDDDDY +⋅⋅+⋅+⋅+= )( 21322110 ββββ

17. ¿Cómo interpretar la interacción?
1β 1β
ii uDDDDY +⋅⋅+⋅+⋅+= )( 21322110 ββββ
1,1 21 == DD
3β
11 =D
1β
12 =D
2β
0,1 21 == DD
1β
0,1 12 == DD
2β

18. Caso 2: interacción entre una
variable dummy y continua
 Considerando el caso básico de un modelo con
una variable dummy y una continua
 Limitación: la pendiente de x1 es independiente de la
variable D1.
 Para liberar esta restricción se introduce un
tercer término:
ii uxDY +⋅+⋅+= 12110 βββ
ii uxDxDY +⋅⋅+⋅+⋅+= )( 11312110 ββββ

19. Interpretación
 Permite un mayor realismo liberar supuestos:
 Realizar hipótesis de variables continuas con cualidades
distintas.
ii uxDxDY +⋅⋅+⋅+⋅+= )( 11312110 ββββ
132
13210
)(
)(ˆ
xY
xY
i
i
∆⋅+=∆
⋅+++=
ββ
ββββ
Si el modelo el lineal, cuando D1=1
el efecto parcial de x1 se resume en
la suma de los coeficientes β2 y β3
estimados.
12
120
ˆ
xY
xY
i
i
∆⋅=∆
⋅+=
β
ββ
Si el modelo el lineal, cuando
D1=0 el efecto parcial de x1 se
resume en el coeficiente β2
estimado.
Fuente: Stock y Watson, 2003

20. Posibles interacciones existentes
Fuente: Stock y Watson, 2003

21.  Considerando el caso básico de un modelo con
una continua
 Al introducir una interacción permite analizar los
efectos parciales de x1 en función de x2:
ii uxxY +⋅+⋅+= 22110 βββ
231
21322110 )(
x
X
Y
uxxxxY ii
⋅+=
∆
∆
+⋅⋅+⋅+⋅+=
ββ
ββββ
Caso 3: interacción entre dos
continuas

22. Ejemplo: suscripciones en librerías

23. Modelo de regresión múltiple
Estimación de modelos no lineales.
Sesión 8
11/marzo/2007