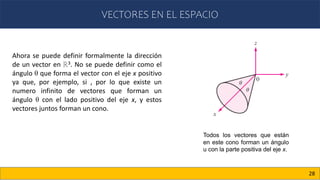
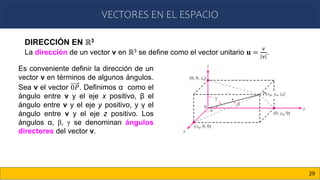
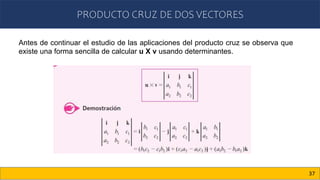
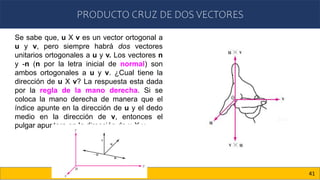
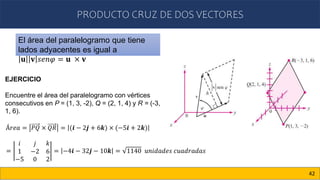
Este documento trata sobre vectores en el plano y en el espacio. Introduce conceptos como vectores en R2 y Rn, producto escalar, producto cruz, ángulo entre vectores, proyecciones de vectores, y vectores en R3. Explica cómo representar puntos y vectores en el espacio tridimensional usando coordenadas cartesianas (x, y, z), y cómo calcular la magnitud y dirección de un vector en R3.



![ÁNGULO ENTRE DOS VECTORES
5
Sean u y v dos vectores diferentes de cero.
Entonces el ángulo φ entre u y v esta
definido como el ángulo no negativo mas
pequeño entre las representaciones de u y v
que tienen el origen como punto inicial. Si u =
αv para algún escalar α, entonces φ = 0 si α
> 0 y φ = π si α < 0 .
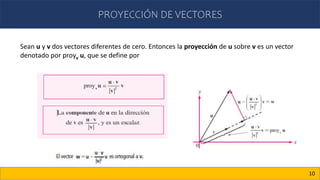
Esta definición se ilustra en la figura. Observe
que φ siempre se puede elegir para que sea
un ángulo no negativo en el intervalo [0, π].](https://image.slidesharecdn.com/clase6algebralineal-230104034612-eb2948b3/85/CLASE_6_ALGEBRA_LINEAL-pptx-5-320.jpg)



![VECTORES ORTOGONALES
9
Los vectores u y v diferentes de cero son ortogonales (o perpendiculares) si el
ángulo entre ellos es
𝜋
2
.
EJEMPLO:
Demuestre que los vectores u = 3i + 4j y v = -4i + 3j son ortogonales.
cosφ=
𝒖·𝒗
𝑢 · 𝑣
= 0
Por lo tanto, como φ esta en el intervalo [0, π], φ =
𝜋
2
.
𝒖·𝒗 = 𝟑 ∗ 𝟒 − 𝟒 ∗ 𝟑 = 𝟎](https://image.slidesharecdn.com/clase6algebralineal-230104034612-eb2948b3/85/CLASE_6_ALGEBRA_LINEAL-pptx-9-320.jpg)