Incrustar presentación
Descargado 29 veces


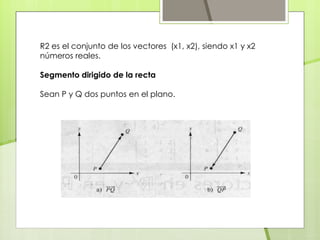
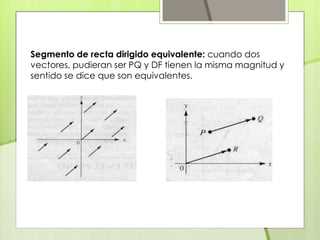


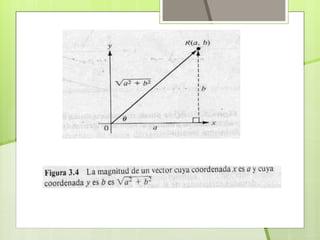







Un vector es una cantidad orientada que tiene magnitud y dirección. Tiene elementos como módulo (longitud), dirección (recta que lo contiene), sentido (orientación) y punto de aplicación (origen). R2 es el conjunto de vectores (x1, x2) donde x1 y x2 son números reales. Dos vectores son equivalentes si tienen la misma magnitud y sentido, como dos segmentos de recta dirigidos PQ y DF. La magnitud de un vector es la longitud de cualquiera de sus representaciones y su dirección es la dirección de sus representaciones.













