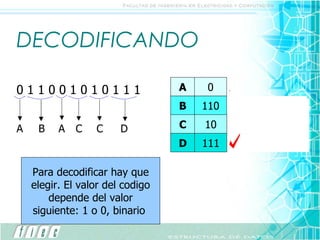
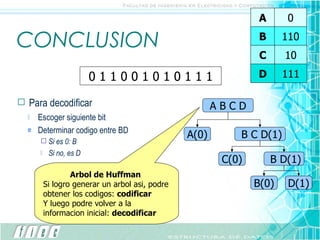
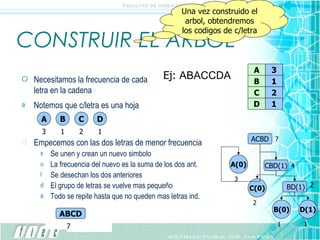
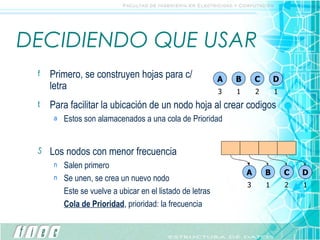
El documento explica el algoritmo de codificación de Huffman, el cual asigna códigos binarios de longitud variable a símbolos basado en su frecuencia de aparición. Primero se construye un árbol de Huffman ordenando los símbolos de menor a mayor frecuencia y uniendo los nodos. Luego, los códigos binarios de cada símbolo se obtienen recorriendo el árbol de raíz a hoja. Esto permite codificar cadenas de texto de manera más compacta.

1. CODIGOS DE HUFFMAN ESTRUCTURAS DE DATOS

7. DECODIFICANDO 0 1 1 0 0 1 0 1 0 1 1 1 A Puede ser B, C o D ? Puede ser B o D ? B A Puede ser B, C o D ? C Puede ser B, C o D C Puede ser B, C o D ? Puede ser B o C ? D Para decodificar hay que elegir. El valor del codigo depende del valor siguiente: 1 o 0, binario A 0 B 110 C 10 D 111

13. DECLARACION DE TDA: ARBOL E INFO typedef struct { string Cadena; int frecuencia; char bit; }Info; Cada elemento del nodo tiene: una cadena, frecuencia y un bit Es ideal agrupar toda esta informacion en un nuevo tipo de dato typedef struct { Generico G; NodoArbol *izq, *der; }NodoAB; Cada Nodo tendra Info, sub. Iza. Y subarbol der:

14. LA COLA DE PRIORIDAD La cola de Prioridad almacenará nodos de Arbol. Se la puede implementar como una lista ordenada o un arreglo Si fuese lista, cada nodo seria y la cola: typedef LSE Cola; typedef struct { Generico G; //La informacion que almacena es NodoAB * NodoCola *sig; }Nodo_LSE;

15. IMPLENTACION: CONSTRUIR ARBOL Arbol ConstruirHuffman(Info_Nodo Frecuencias[], int n){ Cola Q; Info_Arbol I; Arbol nuevo, aizq, ader; VaciarCola(Q); //Construir nodos hojas for(i = 0; i < n; i++){ nuevo = NuevaHoja(Frecuencias[i]); EnCola(Q, nuevo); } //Construir arbol while(TRUE){ aizq = Desencola(Q); ader = Desencola(Q); aizq->I.bit = ‘0’; ader->I.bit = ‘1’; tmp.frec = aizq->I.frec + ader->I.frec; tmp.cadena = StringConcat(aizq->I.cadena, ader->I.cadena); nuevo = NuevaHoja(tmp); nuevo->izq = aizq; nuevo->der = ader; if(QEstaVacia(Q)) break; EnCola(C, nuevo); } return nuevo; }

16. IMPLEMENTACION: ASIGNAR CODIGOS string CodificarLetra(char L, Arbol H){ Arbol p; string strcodigo=“”; p = A; while(!EsHoja(p) && !EstaVacio(p)){ if(FindChar(p->izq->I.cadena, L) >= 0){ strcodigo = Concat(strcodigo, “0”); p = p->izq; } else if (FindChar(p->der->I.cadena, L) >= 0){ strcodigo = Concat(strcodigo, “1”); p = p->der; } else { strcodigo = CopyString(“”); break; } } return strcodigo; }