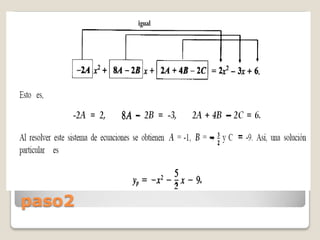
Este documento describe el método de coeficientes indeterminados para resolver ecuaciones diferenciales no homogéneas lineales con coeficientes constantes. Explica que primero se debe determinar la solución complementaria yc de la ecuación homogénea asociada, y luego establecer una solución particular yp probando diferentes formas basadas en la forma del segundo miembro h(x). Proporciona una tabla con las formas probables de yp para diferentes tipos de h(x).

1. Coeficientes
indeterminados
German Eduardo Aceves Gómez
11310003
B:209

2.  Solución general para una ecuación diferencial
lineal no homogéneam Forma de una solución
 particular n Principio de superposición para
ecuaciones diferenciales no homogéneas
 W Casos para aplicar coeficientes indeterminados
Metodo de coeficientes
indeterminados

3. debemos pasar por dos etapas:
 Determinar la función complementaria
yc.
 Establecer cualquier solución particular,
yp, de la ecuación no homogénea.

4. la solución general de en un intervalo es y =yc + yp.
La función complementaria yc es la solución general
de la ecuación homogénea asociada
= 0. En la última sección
vimos cómo resolver estas ecuaciones cuando los
coeficientes son constantes. El primero de dos metodos
que debemos
considerar para obtener una solución particular, yp, se
llama método de los coeficientes
indeterminados.

5. Pueden darse unas reglas para escoger el modelo de
solución particular a probar, en el caso de ecuaciones
lineales con coeficientes constantes y con 2º miembro
h(x) de forma polinómica, exponencial, seno, coseno
o producto de estos dos tipos.
TABLA. Forma de una solución particular yp(x) de
L[y] = h(x), cuando la ecuación tiene coeficientes
constantes; siendo su polinomio característico P(r) y
pp , qp , Pp , Qp , polinomios de grado p.

6. Ejemplo:

7. paso2

8. paso2

9.  La solución general de la ecuación dada es
paso3

10. Tabla de funsiones