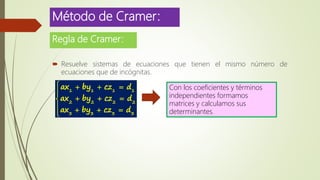
1) El documento presenta diferentes métodos para resolver sistemas de ecuaciones diferenciales, incluyendo el método de eliminación, método de Cramer y método de transformación de Laplace. 2) Como ejemplo, se resuelve un sistema de dos ecuaciones diferenciales usando el método de Cramer y el método de transformación de Laplace. 3) Los métodos permiten reducir sistemas de ecuaciones diferenciales a una forma en que se puedan hallar las soluciones.

1. Métodos empleados para sistema de
ecuaciones diferenciales
PRESENTADO POR :
• Aysana Suarez William Alex
• Borja Camarena Karen Sofía
• Caballon Quispe Mirian Mayumi
• Campos Taype Lizet
“Universidad Nacional del centro del Perú”
Facultad: ingeniería química
Catedra: ECUACIONES DIFERENCIALES

2. Método de eliminación:
 El método de eliminación conocido como reducción o método de
suma y resta consiste en eliminar una de las variables x o y,
 Queda una ecuación con una sola variable,
 Se resuelve, el valor encontrado
 Se sustituye en una de la ecuaciones originales para hallar el valor de
la otra variable.

3. EJERCICIO Nº2:
𝑑𝑥
𝑑𝑡
= 4𝑥 + 7𝑦
𝑑𝑦
𝑑𝑡
= 𝑥 − 2𝑦
Reemplazando en el operador D
𝐷𝑥 − 4𝑥 − 7𝑦 = 0
𝐷𝑦 − 𝑥 − 2𝑦 = 0
Factorizando
𝐷 − 4 𝑥 − 7𝑦 = 0
−𝑥 + 𝐷 + 2 𝑦 = 0
Multiplicamos por (𝑫 − 𝟒)para
eliminar x
𝐷 − 4 𝑥 − 7𝑦 = 0
𝐷 − 4 (−𝑥 + 𝐷 + 2 𝑦 = 0)
(𝐷2−2𝐷 − 15)𝑦 = 0
Las raíces son : 5 y -3
Como son raíces diferentes:
𝑦(𝑡) = 𝐶1𝑒5𝑡
+ 𝐶2𝑒−3𝑡
𝒙(𝒕)
Para hallar 𝒙(𝒕):
Multiplicamos por (𝑫 + 𝟐 ) y 7 para eliminar 𝑦
𝐷 + 2( 𝐷 − 4 𝑥 − 7𝑦 = 0)
7 (−𝑥 + 𝐷 + 2 𝑦 = 0)
(𝐷2
−2𝐷 − 15)𝑥 = 0
(𝐷2
−2𝐷 − 15)=0
Las raíces son : 5 y -3
Como son raíces diferentes:
𝑥(𝑡) = 𝐶3 𝑒 𝑠𝑡
+ 𝐶4 𝑒−3𝑡
Sustituimos en la ecuación original para hallar las constantes 𝐶3 y 𝐶4
𝑑𝑥
𝑑𝑡
= 4𝑥 + 7𝑦
𝑑𝑥
𝑑𝑡
= 𝐶3 𝑒5𝑡
− 3𝐶4 𝑒−3𝑡
5𝐶3 𝑒5𝑡
− 3𝐶4 𝑒−3𝑡
=4(𝐶3 𝑒55𝑡
+ 𝐶4 𝑒−3𝑡
)+7(𝐶1 𝑒5𝑡
+ 𝐶2 𝑒−3𝑡
)
𝐶3 = 7𝐶1 y 𝐶4 = −𝐶2
Reemplazando
𝑦(𝑡) = 𝐶1 𝑒 𝑠𝑡
+ 𝐶2 𝑒−3𝑡
𝑥(𝑡) = 7𝐶1 𝑒 𝑠𝑡
−𝐶2 𝑒−3𝑡

4. Método de Cramer:
 Resuelve sistemas de ecuaciones que tienen el mismo número de
ecuaciones que de incógnitas.
Regla de Cramer:
1 1 1 1
2 2 2 2
3 3 3 3
ax by cz d
ax by cz d
ax by cz d
   

  
   
Con los coeficientes y términos
independientes formamos
matrices y calculamos sus
determinantes.

5. 1 1 1 1
2 2 2 2
3 3 3 3
ax by cz d
ax by cz d
ax by cz d
   

  
   
Determinante
Del sistema
Determinante
de x
Determinante
de y
Determinante
de z
1 1 1
2 2 2
3 3 3
a b c
D a b c
a b c

1 1 1
x 2 2 2
3 3 3
d b c
D d b c
d b c

1 1 1
y 2 2 2
3 3 3
a d c
D a d c
a d c

1 1 1
y 2 2 2
3 3 3
a b d
D a b d
a b d

El valor de cada incógnita es:: x
D
x
D

y
D
y
D
 z
D
z
D

CONDICIONES:
• El sistema que se desea resolver debe ser cuadrado,
es decir, el numero de ecuaciones debe ser igual al
numero de incógnitas.
• La determinante de la matriz del sistema debe ser
diferente de cero

6. EJERCICIO: Nº2
𝑑𝑥
𝑑𝑡
= 4𝑥 + 7𝑦
𝑑𝑦
𝑑𝑡
= 𝑥 − 2𝑦
Reemplazando en el operador D
𝐷𝑥 − 4𝑥 − 7𝑦 = 0
𝐷𝑦 − 𝑥 − 2𝑦 = 0
Factorizando
𝐷 − 4 𝑥 − 7𝑦 = 0
−𝑥 + 𝐷 + 2 𝑦 = 0
Resolviendo por Cramer:
Δ =
(𝐷 − 4) −7
−1 (𝐷 + 2)
Δ = 𝐷 − 4 𝐷 − 2 − 7
Δ = 𝐷2
− 2𝐷 − 15
(𝐷2
−2𝐷 − 15)𝑥 = 0
(𝐷2
−2𝐷 − 15)𝑦 = 0
Las raíces son: 5 y -3
Como son raíces diferentes:
𝑦(𝑡) = 𝐶1 𝑒5𝑡
+ 𝐶2 𝑒−3𝑡
Hallando para 𝒙(𝒕)
(𝐷2−2𝐷 − 15)𝑥 = 0
(𝐷2
−2𝐷 − 15)=0
Las raíces son : 5 y -3
Como son raíces diferentes:
𝑥(𝑡) = 𝐶3 𝑒5𝑡 + 𝐶4 𝑒−3𝑡
Sustituimos en la ecuación original para hallar las
constantes 𝐶3 y 𝐶4
𝑑𝑥
𝑑𝑡
= 4𝑥 + 7𝑦
𝑑𝑥
𝑑𝑡
= 5𝐶3 𝑒5𝑡
− 3𝐶4 𝑒−3𝑡
5𝐶3 𝑒5𝑡
− 3𝐶4 𝑒−3𝑡
=4(𝐶3 𝑒5𝑡
+ 𝐶4 𝑒−3𝑡
)+7(𝐶1 𝑒5𝑡
+ 𝐶2 𝑒−3𝑡
)
𝐶3 = 7𝐶1 y 𝐶4 = −𝐶2
Reemplazando
𝑦(𝑡) = 𝐶1 𝑒 𝑠𝑡
+ 𝐶2 𝑒−3𝑡
𝑥(𝑡) = 7𝐶1 𝑒 𝑠𝑡
−𝐶2 𝑒−3𝑡

7.  Se usa para reducir ciertos sistemas de ecuaciones diferenciales lineales con
condiciones iniciales.
 La transformada de Laplace viene definida por :
Método de transformación
de Laplace:
𝑓 𝑠 =
𝑠0
∞
𝐹(𝑡) 𝑒−𝑠𝑡 𝑑𝑡
Siendo s > 𝑠0
Donde 𝑠0 es el exponente de crecimiento
de 𝐹(𝑡)
L 𝐹(𝑡) = 𝑓 𝑠

8. 1 .- P. de linealidad :
Dada las funciones: 𝑓 𝑡 𝑦 𝑔(𝑡)
ℒ 𝐶1𝑓 𝑡 + 𝐶2𝑔(𝑡) = 𝐶1ℒ 𝑓 𝑡 +C2ℒ 𝑔(𝑡)
2.- P. de cambio de escala:
Sea 𝑓 𝑡 𝜖 𝜀 . La función 𝑔(𝑡) = 𝑓 𝛼𝑡 también pertenece a 𝜀 y se verifica
ℒ 𝑔(𝑡) ≡ 𝐺 𝑠 =
1
𝛼
𝐹
𝑠
𝛼
3.- P. de desplazamiento en frecuencia:
La función 𝑔(𝑡)=𝑒 𝑤𝑡
ℒ 𝑔(𝑡) ≡ 𝐺 𝑠 = 𝐹(𝑠 − 𝑤)
PROPIEDADES:

9. 4.- P. transformada de laplace de la deriada primera de una funcion:
ℒ 𝑓′(𝑡) = 𝑠 𝐹(𝑠) − 𝑓(0)
Siendo F s = ℒ 𝑓 𝑡 𝑦 𝑓 0 𝑒𝑙 𝑣𝑎𝑙𝑜𝑟 𝑑𝑒 𝑙𝑎 𝑓𝑢𝑛𝑐𝑖𝑜𝑛𝑑𝑒 𝑜𝑟𝑖𝑔𝑒𝑛
5.-P. transformada de laplace de la primitiva de una función:
Sea 𝑓 𝑡 ∈ 𝜀. Su primitiva g(t) = 0
𝑡
𝑓 𝑡 𝑑𝑡 es una función continua y de orden exponencial
y su transformada de Laplace viene dada por
ℒ 𝑔(𝑡) ≡ 𝐺 𝑠 = −
1
𝑠
𝐹(𝑠)
6.-P. convolucion de dos funciones:
Sean 𝑓 𝑡 y g 𝑡 pertenecientes a 𝜀. La función ℎ 𝑡 definida por la convolucion de de f y
ℎ 𝑡 = (𝑓 ∗ 𝑔) =
0
𝑡
𝑓 𝑡 − 𝜏 𝑔 𝜏 𝑑𝜏

11.  las incógnitas son ahora las transformadas de las funciones de las funciones que
conforman la solución
 Al despejar estas incógnitas y calcular sus transformadas inversas de Laplace se
obtiene la solución del problema con valores iniciales para el sistema:
TRANSFORMADA
INVERSA DE LAPLACE:
Si 𝐹(𝑠) es la transformada de Laplace de una función continua 𝑓(𝑡) , es decir
ℒ 𝑓(𝑡) = 𝐹(𝑠)
Entonces la transformada inversa de Laplace de 𝐹(𝑠) es:
ℒ−1
𝐹(𝑠) = 𝑓(𝑡)

12. Ejercicio: de Zill Nº 1
𝑑𝑥
𝑑𝑡
= −𝑥 + 𝑦
𝑑𝑦
𝑑𝑡
= 2𝑥
𝑥(0) = 0 𝑦(0) = 1
SOLUCIÓN:
ℒ
𝑑𝑥
𝑑𝑡
+ ℒ 𝑥 − ℒ 𝑦 = 0
ℒ
𝑑𝑦
𝑑𝑡
− ℒ 2𝑥 = 0
𝑠𝑥(𝑠) − 𝑥 0 + 𝑥 𝑠 − 𝑦 𝑠 = 0
𝑠𝑦(𝑠) − 𝑦 0 − 2𝑥 𝑠 = 0
Factor izando y reemplazando los valores
iniciales:
(𝑠 + 1)𝑥(𝑠) − 𝑦 𝑠 = 0
−2𝑥 𝑠 + 𝑠𝑦(𝑠) = 1
Utilizando la regla de cramer:
𝑥(𝑠) =
0 𝑠+1
1 −2
𝑠+1 −1
−2 𝑠
=
−(𝑠+1)
𝑠2+𝑠−2
=
−(𝑠+1)
(𝑠+2)(𝑠−1)
Por fracciones parciales:
−(𝑠+1)
(𝑠+2)(𝑠−1)
=
𝐴
(𝑠+2)
+
𝐵
(𝑠−1)
DONDE:
𝐴 = −
1
3
y B= −
2
3
Utilizando la transformada de la inversa
𝑥(𝑡) = ℒ−1
𝑥(𝑠)
𝑥(𝑡) = ℒ−1
−1/3
(𝑠 + 2)
+
−2/3
(𝑠 − 1)
𝑥(𝑡) = ℒ−1
−1/3
(𝑠 + 2)
+ ℒ−1
−2/3
(𝑠 − 1)
𝑥(𝑡) = −1/3𝑒−2𝑡
− 2/3𝑒 𝑡

13. Hallando 𝒚(𝒔)
𝑦(𝑠) =
𝑠+1 0
−2 1
𝑠+1 −1
−2 𝑠
=
𝑠+1
𝑠2+𝑠−2
=
𝐶
(𝑠+2)
+
𝐷
(𝑠−1)
DONDE:
𝐶 =
1
3
y D =
2
3
Utilizando la transformada de la inversa
𝑦(𝑡) = ℒ−1
𝑦(𝑠)
𝑦(𝑡) = ℒ−1
1/3
(𝑠 + 2)
+
2/3
(𝑠 − 1)
𝑦(𝑡) = ℒ−1
1/3
(𝑠 + 2)
+ ℒ−1
2/3
(𝑠 − 1)
𝑥(𝑡) = 1/3𝑒−2𝑡
+ 2/3𝑒 𝑡
La solución esta dada por:
𝑥(𝑡) = 1/3𝑒−2𝑡 + 2/3𝑒 𝑡
𝑦(𝑡) = −1/3𝑒−2𝑡 − 2/3𝑒 𝑡