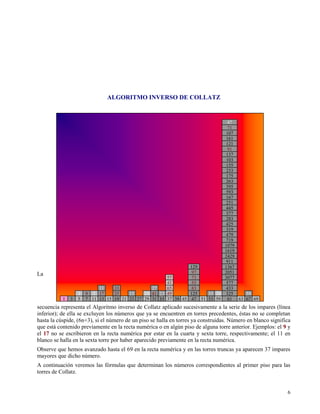
Este documento presenta un resumen de tres oraciones del concepto y algoritmo de Collatz, también conocido como el problema 3n+1. Explica que el algoritmo de Collatz propone que aplicando sucesivas operaciones de triplicar y sumar 1 o dividir por 2 a cualquier número entero positivo, eventualmente se llegará al número 1. Además, introduce la noción de "torres de Collatz" para organizar los números generados por el algoritmo y la "autopista de Collatz" formada por una sucesión ordenada de estas torres.

1. VIAJE DE FANTASÍA<br />Usted va de viaje en su flamante auto, su cerebro se trastorna y de pronto ingresa a una extraña autopista. A su derecha empieza una sucesión de torres numeradas en su parte alta con la serie 3, 9, 15, 21, 27, ... <br />En su recorrido hacia el infinito observará torres de uno, varios o muchos pisos, a una torre unipiso la podrá suceder un enorme rascacielos o a la inversa. Su fantasioso viaje no es otra cosa que la visión del famoso Algoritmo de Collatz o Problema 3n + 1.<br />Detiene su auto al frente de uno de los inmensos rascacielos, ingresa y asciende a la azotea. A la izquierda de la autopista aparecerán ciudades identificadas con numerales como 13, 53, 85, y a sus alrededores diminutas viviendas unipiso; ciudades y viviendas entre las cuales no existen vías de comunicación. <br />Piensa que los habitantes de cada ciudad o vivienda son personas alérgicas a establecer contacto con las demás urbes. Investiga y su presunción desaparece, todos se conectan por debajo de tierra. Las vías subterráneas representan la denominada Conjetura de Collatz: hacia la superficie conducen a toda torre y hacia abajo se encuentra el COMPLEJO GUBERNAMENTAL 1. <br />En cada vivienda o piso de una torre tan solo hay un personaje, dicho personaje se identifica con un número impar, si encuentra dos personajes con la misma identificación significa que está recorriendo un universo de expertos clonadores.<br />El SUPREMO JEFE 1, buen especialista en delegar funciones, tiene como Vicepresidente al 5. El Vicepresidente ejerce el mando directo sobre un conglomerado de torres y el Presidente lo ejerce sobre otro: ningún gobernado directo del Presidente lo es del Vicepresidente y a la inversa.<br />Termina su trastorno, pasa algún tiempo en sano juicio. <br />Su sueño transcurre en calma, el inconsciente entra en acción e intenta recorrer de nuevo la Autopista de Collatz: las torres unipiso del recorrido inicial han desaparecido. Despierta con la extrañeza del cambio con respecto a su visión del primer viaje. ¿Qué ha sucedido?<br />220853018415000<br />LA CONJETURA DE LÖTHAR COLLATZ <br />Collatz, en 1937, formuló la conjetura que posee el récord de nombres: Problema 3n +1, Cartografía 3x + 1, Algoritmo de Hasse, Problema de Kakutani, Algoritmo de Syracuse, Conjetura de Thwaites y Problema de Ulam. <br />El algoritmo de Collatz dice: <br />Inicie con cualquier número par, divida sucesivamente por 2 hasta que obtenga un impar; triplique el resultado, sume 1 y divida por dos hasta obtener otro número impar. Repita el proceso. Siempre llegará a 1 para todo número de inicio (Conjetura).<br />Inicie con uno impar, realice las reglas del juego (triplicar y sumar 1, luego dividir por 2) e igual llegará a 1. (Conjetura).<br />197993025831803 5 1 3 5 10 16 48 2 1 003 5 1 3 5 10 16 48 2 1 791210114300 ALGORITMO Y CONJETURA DE LÖTHAR COLLATZ 00 ALGORITMO Y CONJETURA DE LÖTHAR COLLATZ <br />Los resultados de la sucesión del algoritmo de Collatz se denominan números de granizo. Aquí los llamaremos granizos.<br />Tal como se muestra en el ejemplo anterior, en este documento prescindiremos de los números pares y, en lo sucesivo, solo registraremos los impares. La razón es que de esta forma estaremos en buenas condiciones para demostrar la conjetura. <br />Otra de las razones por las cuales no emplearemos los números pares es que, en el fondo, el algoritmo de Collatz es más bien una forma algo «enrevesada» de construir el conjunto de los impares mediante un ordenamiento no estándar.<br />Lo «enrevesado» de la construcción del conjunto de los impares mediante el algoritmo de Collatz explica la dificultad por la cual, antes de este documento, no se logró la demostración de la Conjetura de Collatz.<br />ALGORITMO INVERSO DE COLLATZ<br />Inicie con cualquier número impar que no sea múltiplo de 3, multiplique sucesivamente por 2 hasta que el resultado disminuido en 1 sea múltiplo de 3, divida por 3 y aplique de nuevo el algoritmo. Conjetura: Exceptuando n = 1, siempre se finaliza en un múltiplo de 3.<br />6083302152659713 111751351TORRES DE COLLATZDenominaremos Torres de Collatz a los granizos impares generados por números de la forma 6n + 3 (Cúspide de la Torre)Para los efectos de este documento, en lo sucesivo, el concepto de torre no incluirá los granizos 1 ni 5.Suponga que se encuentra en la cúspide de una torre de Collatz con la prohibición de descenso a cualquier piso inferior y, al mismo tiempo, le exigen seguir aplicando el Algoritmo inverso de Collatz. Se concluye que se encuentra frente a un «absurdo» matemático dado que ningún múltiplo de disminuido en 1 puede ser divisor de 3. Además, Ascendiendo o descendiendo, tendría que repetir los mismos números sin poder salir de la torre. Sin embargo, ¡el «absurdo» tiene solución!9713 1117ABSURDO EN LA CÚSPIDE 009713 111751351TORRES DE COLLATZDenominaremos Torres de Collatz a los granizos impares generados por números de la forma 6n + 3 (Cúspide de la Torre)Para los efectos de este documento, en lo sucesivo, el concepto de torre no incluirá los granizos 1 ni 5.Suponga que se encuentra en la cúspide de una torre de Collatz con la prohibición de descenso a cualquier piso inferior y, al mismo tiempo, le exigen seguir aplicando el Algoritmo inverso de Collatz. Se concluye que se encuentra frente a un «absurdo» matemático dado que ningún múltiplo de disminuido en 1 puede ser divisor de 3. Además, Ascendiendo o descendiendo, tendría que repetir los mismos números sin poder salir de la torre. Sin embargo, ¡el «absurdo» tiene solución!9713 1117ABSURDO EN LA CÚSPIDE <br />Dividiremos nuestro trabajo en dos partes: Construcción Collatz del conjunto de los impares y demostración de la conjetura. <br />CONSTRUCCIÓN COLLATZ <br />DEL CONJUNTO DE LOS IMPARES<br />Se denominará Torre de Collatz a una columna de números impares que en su parte más elevada, cúspide, contenga un número de forma 6n + 3 y en la parte inferior uno de forma o Los demás pisos se conforman con los granizos impares, excepto el 1 y el 5.<br />RECTA DE COLLATZ <br />7099301682751 2135313334138535213418554611365001 2135313334138535213418554611365<br />AUTOPISTA DE COLLATZ<br />Se denominará Autopista de Collatz a la sucesión ordenada de torres de conformidad con el numeral correspondiente la cúspide. <br />1202690165100271521395145393363570027152139514539336357<br />Para conocer los números ubicados en los pisos inferiores se aplica el algoritmo de Collatz hasta llegar al primer piso.<br />En la página siguiente aparece la Autopista de Collatz desde la Torre 3 hasta la Torre 129 (22 torres), tramo en el que se encuentran los números impares menores que 100. Luego hemos separado la autopista en ciudades que se distinguen por tener todas sus torres con el mismo número en el piso inferior. Observará las ciudades 13, 53 y 85 con agregación de otras torres.<br />20713703873500<br />28829020002515 53 3523213 9 71117 132741 31 47 71 107 161 121 91137 103155233175263395593445167251377283425319479719107916192429911136720513077577433325612353 3525 1119 293317 13395989671011119 2917 1345 17 135129771117 13743654937571117 136395143215323485 91137 103155233175263395593445167251377283425319479719107916192429911136720513077577433325612353 3569131138575871311973771117 139335539914971117 136153 352381192910579119 2691791011117 13111445167251377283425319479719107916192429911136720513077577433325612353 35117111713 123185 1392091575989 67101 1929 11 17 13 12997 73558312591137 103155233175263395593445167251377283425319479719107916192429911136720513077577433325612353 3547 71107 161121 0015 53 3523213 9 71117 132741 31 47 71 107 161 121 91137 103155233175263395593445167251377283425319479719107916192429911136720513077577433325612353 3525 1119 293317 13395989671011119 2917 1345 17 135129771117 13743654937571117 136395143215323485 91137 103155233175263395593445167251377283425319479719107916192429911136720513077577433325612353 3569131138575871311973771117 139335539914971117 136153 352381192910579119 2691791011117 13111445167251377283425319479719107916192429911136720513077577433325612353 35117111713 123185 1392091575989 67101 1929 11 17 13 12997 73558312591137 103155233175263395593445167251377283425319479719107916192429911136720513077577433325612353 3547 71107 161121 <br />171371191317 451369131929332517111337435749657171113 8967101593929191711137751291711371971318717117131711713149991051711291310126917919119791711117135915713920917112913101678919123185<br />53 3515 2347 3127 41121 16171 107 155 103 91 137 395 263 233 175 445 251 593167 319 425 377 283 16191079479719205113672429911325433307757753356123155 103 91 137 395 263 233 175 445 251 593167 319 425 377 283 161910794797192051136724299113254333077577533561232151436395323485539335815335612347 12555 83121 16171 107 155 103 91 137 395 263 233 175 445 251 593167 319 425 377 283 161910794797192051136724299113254333077577533561237312997445 251 111167 319 425 377 283 161910794797192051136724299113254333077577533561235314147 125221 83121 16171 107 155 103 91 137 395 263 233 175 445 251 593167 319 425 377 283 16191079479719205113672429911325433307757753356123147539359159239809607205113679113254333077577533561231425 401 30111385 1069 301 113851605 453 85 75 113 85 401 30111385 267 1205 11385803 633 475713535 85 951 2141 8031205 113 1427 <br />ALGORITMO INVERSO DE COLLATZ<br />47117023558547121 16171 107 155 103 91 137 395 263 233 175 445 251 593167 319 425 377 283 1619107947971920511367242991132543330775776139593553511523251933211571117 13 111359733957434937652335413127192927454783125129977355696359670047121 16171 107 155 103 91 137 395 263 233 175 445 251 593167 319 425 377 283 1619107947971920511367242991132543330775776139593553511523251933211571117 13 11135973395743493765233541312719292745478312512997735569635967<br /> <br />La secuencia representa el Algoritmo inverso de Collatz aplicado sucesivamente a la serie de los impares (línea inferior); de ella se excluyen los números que ya se encuentren en torres precedentes, éstas no se completan hasta la cúspide, (6n+3), si el número de un piso se halla en torres ya construidas. Número en blanco significa que está contenido previamente en la recta numérica o en algún piso de alguna torre anterior. Ejemplos: el 9 y el 17 no se escribieron en la recta numérica por estar en la cuarta y sexta torre, respectivamente; el 11 en blanco se halla en la sexta torre por haber aparecido previamente en la recta numérica.<br />Observe que hemos avanzado hasta el 69 en la recta numérica y en las torres truncas ya aparecen 37 impares mayores que dicho número.<br />A continuación veremos las fórmulas que determinan los números correspondientes al primer piso para las torres de Collatz. <br />TORRES QUE NO CONTIENEN EL GRANIZO 5<br />Si se aplica el Algoritmo de Collatz observaremos que hay dos clases de torres: un grupo de ellas no contiene el granizo 5 y el otro grupo lo contiene. En el primer caso diremos que la torre desciende directamente a 1 y en el otro el descenso a 1 se realiza a través de 5.<br />GRUPO DE DESCENSO DIRECTO A 1<br />471170161925Por cualquiera de estos números se puede ascender (algoritmo inverso de Collatz); ello implica, necesariamente, el descenso a 1 (Conjetura de Collatz) descenso directo.155 46121 845 349 52587 3811 365 3418521u00Por cualquiera de estos números se puede ascender (algoritmo inverso de Collatz); ello implica, necesariamente, el descenso a 1 (Conjetura de Collatz) descenso directo.155 46121 845 349 52587 3811 365 3418521u<br />GRUPO DE DESCENSO A TRAVÉS DE 5<br />699770-63521313 653133 4138535354 6135 1 3Por cualquiera de estos números se puede ascender (algoritmo inverso de Collatz); ello implica, necesariamente, el descenso a 1 (Conjetura de Collatz) a través de 5. u0021313 653133 4138535354 6135 1 3Por cualquiera de estos números se puede ascender (algoritmo inverso de Collatz); ello implica, necesariamente, el descenso a 1 (Conjetura de Collatz) a través de 5. u<br />97409073660EFECTO COLLATZ00EFECTO COLLATZ<br />56261024765TEOREMA TIERRA (Primer piso de las torres)Todo número o cumple la conjetura de Collatz.Demostración00TEOREMA TIERRA (Primer piso de las torres)Todo número o cumple la conjetura de Collatz.Demostración<br />El Teorema Tierra indica que las torres tendrán un piso para múltiplos de 3 generados por las fórmulas anteriores y que no se requiere verificación dada su demostración genérica. Si a los no múltiplos de 3 se les aplica el algoritmo inverso de Collatz entonces los resultados descenderán, necesariamente, a 1 por el Algoritmo de Collatz. (Ley de regresión de los algoritmos). Igual significa que tienen uno o dos niveles en el sótano: 1 para el grupo de descenso directo y 5, 1 para el otro.<br />129413087630TEOREMA TIERRA3 13 53 213 5 21 85 341 1 00TEOREMA TIERRA3 13 53 213 5 21 85 341 1 <br />74549024765Suponga que se encuentra en la cúspide de una torre de Collatz con la prohibición de descenso a cualquier piso inferior y, al mismo tiempo, le exigen seguir aplicando el Algoritmo inverso de Collatz. Se concluye que se encuentra frente a un «absurdo» matemático dado que ningún múltiplo de disminuido en 1 puede ser divisor de 3. Además, Ascendiendo o descendiendo, tendría que repetir los mismos números sin poder salir de la torre. Sin embargo, ¡el «absurdo» tiene solución!9713 1117 ABSURDO EN LA CÚSPIDE 00Suponga que se encuentra en la cúspide de una torre de Collatz con la prohibición de descenso a cualquier piso inferior y, al mismo tiempo, le exigen seguir aplicando el Algoritmo inverso de Collatz. Se concluye que se encuentra frente a un «absurdo» matemático dado que ningún múltiplo de disminuido en 1 puede ser divisor de 3. Además, Ascendiendo o descendiendo, tendría que repetir los mismos números sin poder salir de la torre. Sin embargo, ¡el «absurdo» tiene solución!9713 1117 ABSURDO EN LA CÚSPIDE <br /> <br />El «absurdo» anterior tiene su campo de validez tan solo en el marco de cada torre debido a que el Algoritmo de Collatz determina series finitas de granizos o, en términos de las torres, son series verticales «acotadas» En lenguaje más técnico diríamos que son series cerradas.<br />El «absurdo» propuesto podría denominarse PARADOJA DE COLLATZ dado que, sin violar la prohibición, siempre es posible el ascenso hacia el infinito. Recuerde que lo único que le prohiben es el descenso.<br />PUENTE <br />La Paradoja de Collatz se resuelve mediante la operación que denominaremos Puente <br />Veamos un ejemplo del Puente antes de proceder a su demostración general. Suponga que se encuentra en la cúspide 9; todo múltiplo par de 9 lo es de 3 y, por tanto, al restar 1 es imposible obtener un número impar divisible por 3. Nos exigen ascender sin alusión a la cúspide; en consecuencia, nuestro ascenso se debe realizar a partir de 7, sin descenso a dicho número. <br />Efectuemos 4 x 9 + 1 = 37, 4 x 261 + 1 = 1 045, 4 x 1 857 + 1 = 7 429 ... y, en cada caso, apliquemos el Algoritmo inverso de Collatz hasta alcanzar la cúspide de la correspondiente torre.<br /> <br />12026901200159 7111713 37 7111713 26149 1857139337 7111713 104549 ASCENSO AL INFINITO009 7111713 37 7111713 26149 1857139337 7111713 104549 ASCENSO AL INFINITO<br />33401024765LEY MATEMÁTICA QUE RIGE A DOS GRANIZOS IMPARES SUCESIVOS00LEY MATEMÁTICA QUE RIGE A DOS GRANIZOS IMPARES SUCESIVOS<br />En lenguaje común el Algoritmo de Collatz se expresa así: Multiplique un impar por 3, agregue 1, el resultado es un par, divida este último valor por la mayor potencia de 2 contenida en él y obtendrá otro impar. <br />La conjetura afirma que la repetición sucesiva del algoritmo finaliza en el granizo 1 o, en otras palabras, llegará al ciclo 1, 1, 1, ...<br />MERITORIO Y JUSTO HOMENAJE<br />Wailly, el Webmáster permanente de este portal, es el revisor que evita la filtración de errores de diferentes clases antes de que los aportes del autor lleguen a Usted.<br />Wailly consulta en Internet los documentos que puedan servir de materia prima para la realización del trabajo propio de www.matematicainsolita.8m.com <br />La Conjetura de Collatz era desconocida para quien escribe y gracias al Webmáster este documento se hizo posible.<br />Trabajando con el algoritmo 3n + 1 partí de un hipotético 4a + 1, le apliqué transformaciones y llegué a otro hipotético <br />Inicié la aplicación del algoritmo al número 27; luego de muchas operaciones empecé a pensar que el conjeturado 1, si aparecía, exigiría demasiadas iteraciones. <br />Solicité a Wailly que continuara operando y luego de 4 iteraciones dijo: ¡Listo!. Miré y no observé el ansiado 1. Wailly respondió que no era necesario continuar debido a que el proceso se lo había aplicado al 911 y, por tanto, los números subsiguientes serían los mismos. Revisó las tablas y confirmó las palabras con los datos.<br />Afirmó, además, que para cualquier número de inicio era suficiente con llegar a un resultado conocido y por lógica del algoritmo el proceso conduciría a 1.<br />Como MERITORIO Y JUSTO HOMENAJE a la persona que ha hecho posible que Usted se beneficie de <br />www.matematicainsolita.8m.com, la formulación y demostración del Puente se denominarán TEOREMA DE WAILLY.<br />56261039370TEOREMA DE WAILLYLos pisos inferiores de cualquier pareja de torres con granizos diferentes de forma son iguales a los subsiguientes de DEMOSTRACIÓN: El TEOREMA DE WAILLY es generalización del Teorema Tierra e indica que existe una infinidad de números que convergen a w1, además de w0 que genera a w1 de acuerdo con o, desde la óptica del algoritmo inverso, existe una infinidad de ramificaciones para w1w0w1ESQUEMA GENÉRICO DEL PUENTE 4w + 1PUENTE 4w + 1 y TEOREMA DE WAILLYw0w1w2 w3wf 6a+3 uw3w2 w1wf4w0 + 1......00TEOREMA DE WAILLYLos pisos inferiores de cualquier pareja de torres con granizos diferentes de forma son iguales a los subsiguientes de DEMOSTRACIÓN: El TEOREMA DE WAILLY es generalización del Teorema Tierra e indica que existe una infinidad de números que convergen a w1, además de w0 que genera a w1 de acuerdo con o, desde la óptica del algoritmo inverso, existe una infinidad de ramificaciones para w1w0w1ESQUEMA GENÉRICO DEL PUENTE 4w + 1PUENTE 4w + 1 y TEOREMA DE WAILLYw0w1w2 w3wf 6a+3 uw3w2 w1wf4w0 + 1......<br />REGLAS DEL PUENTE 4w + 1w0 = 4m + 1 w0 = 4m + 3 29011713 9 7111713 451713 1811713 7251713 Ejemplo:DEMOSTRACIÓN DE LA CONJETURA DE COLLATZLas torres 3, 9, 15, 21,... , 129 descienden a 1 (Demostración exhaustiva)Un impar cualquiera pertenece a la torre 129, a una anterior o a una posterior (de lo contrario el Algoritmo 3n + 1 sería inoperante)Todo granizo de una torre genera infinidad de nuevas torres (Puente 4w + 1)Las torres subsiguientes a la 129 se conectan a ésta, o a una anterior, mediante el Puente 4w + 1Por tanto, todo impar desciende a 1 al serle aplicado el Algoritmo 3n + 1COROLARIO: El Algoritmo 3n + 1 implica el descenso a 1 para todo par.<br /> <br /> <br />ALGORITMO 3n + 1 EN LOS ENTEROS NEGATIVOS<br />El Algoritmo de Collatz actúa de igual forma al ser aplicado al conjunto de los enteros negativos y equivale al algoritmo en los naturales. La diferencia consiste en que no habrá un único valor al cual se descienda.<br />Ciclos. Se denomina ciclo a los granizos que determinan una serie cerrada al ser aplicado el algoritmo a cualquiera de sus elementos, en otras palabras, el algoritmo es una operación cerrada para el ciclo. En el caso de los naturales solo existe el ciclo {1} para el algoritmo 3n + 1. En el de los enteros negativos se conoce la existencia de tres ciclos para el mismo algoritmo; si existe otro habría que hallarlo o demostrar la imposibilidad de que exista. <br />En términos cotidianos el ciclo es definible como la manecilla de un reloj: siempre marcará los mismos números en el mismo orden.<br />CICLOS PARA EL ALGORITMO <br /> <br />Es forzoso concluir que el algoritmo genera una partición del conjunto de los impares en 3 conjuntos en virtud de que dichos ciclos carecen de elementos comunes. <br />6997701149353 1115 11 91351972131231727549331097317916116329391435119 7567459117253761554153715785 12795 597911147635 71913357755 103 691 43 115 77 121 8119 203271 181 5 765 87325217 145 971 43 115 307 205 547 365 4875 7 19 13 139 9337 999117615541003 1115 11 91351972131231727549331097317916116329391435119 7567459117253761554153715785 12795 597911147635 71913357755 103 691 43 115 77 121 8119 203271 181 5 765 87325217 145 971 43 115 307 205 547 365 4875 7 19 13 139 9337 999117615541<br />42545017145ALGORITMO 3n + 1Puente: 4w + 1ALGORITMO Puente: 4w - 100ALGORITMO 3n + 1Puente: 4w + 1ALGORITMO Puente: 4w - 1<br /> <br />ALGORITMO <br /> <br />Si existe Puente entonces se debe encontrar el valor de k (único) empleando cualquier pareja de granizos impares en la ecuación <br />El Puente permite conjeturar el descenso de cualquier número a uno u otro ciclo. En el caso del Algoritmo es demostrable la inexistencia del Puente. <br />COMENTARIOS A TRAVÉS DEL ALGORITMO <br /> <br />Dado que existe Puente y un ciclo, es posible conjeturar el descenso de todo número a dicho ciclo (ciclos, de existir otros). <br />La demostración exigiría construir la serie de torres de cúspide 7, 21, 35, 49,... para verificar (demostración exhaustiva) el descenso de los granizos de las mismas al ciclo (ciclos) y luego, mediante el principio de interconexión (Puente), realizar la demostración general de la conjetura. En el caso de varios ciclos se acudiría para efectos demostrativos, agotada la parte exhaustiva, a un supuesto ciclo único (isomorfismo). <br />Es probable que usted desista de sus intentos de viajar de 7 a 1 a bordo del algoritmo . Dicho viaje será exitoso cuando llegue al primer w tal que La incertidumbre que le generen las torres de cúspide 7, 21, 35, 49, al aplicarles el algoritmo lo llevarán a sospechar que ninguna llegará al ciclo; en matemáticas no es suficiente con sospechar. <br />Si aplica el algoritmo a la torre 299593 llega a 1 al instante: multiplique por 7, agregue 1 y dedíquese a dividir por 2. En el caso de las torres 329 y 86 282 825 llegará al ciclo a través de 9 (multiplicando y sumando solo 2 veces).<br />Mediante funciones es fácil demostrar que existen infinidades de torres que alcanzan el ciclo; sin embargo, se trata de demostrar que la totalidad de torres llegan al mismo (si lo alcanzan) para que la conjetura se transforme en teorema.<br />Existen números fuera de torres 7(2m+1) pero conectados a ellas mediante el puente 8w + 1; Ejemplo: 3, por ser , 3 se conecta a la torre 7 mediante 8(3) + 1 = 25. Algo similar sucede con 5 y 41, conectados a la torre 329. Las torres de cúspide diferente a 7(2m+1) no afectan el proceso demostrativo (de ser cierta la conjetura) debido a que el Teorema de Wailly garantiza que los granizos inferiores son los mismos para torres interconectadas: si una de ellas no desciende al ciclo tampoco lo hará la otra, el descenso de una implica el descenso de la otra.<br />Nota: Los modelos matemáticos que definiremos a continuación están referidos a granizos impares: por tanto, n, c serán impares en las fórmulas definitorias.<br />MODELO GENERAL DE COLLATZAlgoritmo: Puente: Ciclo: Interrogantes: ¿La aplicación de cualquier algoritmo del Modelo General de Collatz implica el descenso a 1? ¿Cuáles implican el descenso a 1? El modelo general, cuando m = 1, es de uso corriente en las matemáticas y de ahí deriva el hecho de no ponerse en discusión. Dicho modelo se puede estudiar de la misma forma que se hizo con el algoritmo 3n + 1.Algoritmo: Puente: Ciclo: Para el algoritmo las cúspides de las torres son la serie de los impares y el número de llegada es el 1. No olvide que las torres las formamos con los granizos impares. En este caso todo granizo es cúspide, analice el segundo piso (rosado).5311317131951131137115117953119531211131233125137127712915131133179531ULTRA MODELO LÖTHAR COLLATZAlgoritmo: Puente: Ciclos: , El algoritmo 7n + 5 tiene, al menos, los ciclos y Interrogantes: ¿La aplicación de cualquier algoritmo del Ultra Modelo Löthar Collatz implica el descenso a los ciclos para todo número natural? ¿Qué algoritmos del Ultra Modelo Löthar Collatz implicarían el descenso a los ciclos para todo número natural? <br /> <br /> <br /> <br />INDUCCIÓN ALGORÍTMICA AL TRABAJO INFRUCTUOSO<br />Al leer «COMENTARIOS A TRAVÉS DEL ALGORITMO 7n + 1» es muy probable que Usted haya enfrentado la tarea de saber si era posible alcanzar el ciclo 1aplicando dicho algoritmo a 7: quizá desistió del intento después de recorrer muchos granizos quitándole tiempo a sus horas de descanso.<br />Su trabajo se plasmó en sospecha e impotencia al no poder confirmar o desechar las dudas. Uno de sus proyectos para enfrentar el problema pudo ser la construcción de un programa de ordenador.<br /> «A través de programas de ordenador se ha probado que la Conjetura de Collatz es cierta para todo » es una información que muestra la impotencia de quien haya empleado el programa que en nada contribuye a solucionar la conjetura. Informaciones de ese tipo producen la sensación de matemáticos que actúan como escolares que resuelven cientos de operaciones por imposición de su maestro.<br />Muchos matemáticos aplican los algoritmos siguiendo siempre la corriente de los mismos; raras veces se detienen en el análisis del algoritmo inverso. Si usted estudia los trabajos con respecto a la Conjetura de Collatz se dará cuenta de lo afirmado. <br />Las explicaciones de dicha costumbre se dejan al lector.<br />El problema de saber si es posible alcanzar 1, aplicando el algoritmo 7n + 1 al número 7, se puede resolver sin acudir al algoritmo ni a un programa de ordenador: aplique el algoritmo inverso a 1. Requiere unas pocas operaciones, lógica aritmética elemental y no necesita calculadora; el puente 8n + 1 le servirá de auxiliar.<br />Respuesta afirmativa (1 asciende a 7) implica comenzar a conjeturar que todo número desciende a 1 aplicando el algoritmo 7n + 1. Si su respuesta es negativa (1 no asciende a 7) entonces ha demostrado que la conjetura no es válida para todo número.<br />OBSERVACIONES FUERA DE ÓRBITA <br />Muchos matemáticos talentosos piensan que para conocer las leyes que gobiernan la distribución de los primos en el conjunto de los naturales es necesario resolver la Hipótesis de Riemman e igual para demostrar la Conjetura de Goldbach y otras. El trabajo realizado en www.numerosprimos.8m.com muestra que dichas leyes se pueden determinar sin acudir a la demostración de la Hipótesis de Riemman. Para ello basta con determinar la función (la fórmula de Gauss es una aproximante), con ella demostrar que y emplear el sencillo procedimiento aritmético de hallar la cantidad de números en el intervalo [a, b] mediante la función .<br />Para demostrar el Último Teorema de Fermat no es obligatorio el difícil y extenso andamiaje de las curvas elípticas empleadas por el Doctor Andrew Wiles (matemático inglés).<br />161417078105En ocasiones es más fácil nadar contra la corriente, al menos, en matemáticas.00En ocasiones es más fácil nadar contra la corriente, al menos, en matemáticas. <br /> <br />ALGORITMOS 3n + 1 y 7n + 1: GRAFOS IMPARES<br />Los siguientes grafos parciales muestran el comportamiento de los granizos impares. En la parte superior aparece el correspondiente ciclo (cuadro anaranjado), debajo del mismo se observa el resultado de aplicarle el puente. Pasando por estos dos valores imagine un eje vertical.<br />Aplique el algoritmo a los números mostrados en el grafo y comprenderá los demás aspectos. Luego aplique el algoritmo inverso.<br />882650123190511 365 341 218517117935¿¿ 23151332135311322715175201GRAFO 3n +1La línea verde indica la aplicación del puente 4n + 1 (hacia abajo).La azul representa la aplicación del algoritmo inverso 3n + 1(hacia la derecha o hacia la izquierda, según el caso) 91?167??37449 468173585?¿¿ ?¿¿ ?30094152 633329?GRAFO 7n +1La línea verde indica la aplicación del puente 8n + 1 (hacia abajo).La azul representa la aplicación del algoritmo inverso 7n + 1 (hacia la derecha o hacia la izquierda, según el caso) 00511 365 341 218517117935¿¿ 23151332135311322715175201GRAFO 3n +1La línea verde indica la aplicación del puente 4n + 1 (hacia abajo).La azul representa la aplicación del algoritmo inverso 3n + 1(hacia la derecha o hacia la izquierda, según el caso) 91?167??37449 468173585?¿¿ ?¿¿ ?30094152 633329?GRAFO 7n +1La línea verde indica la aplicación del puente 8n + 1 (hacia abajo).La azul representa la aplicación del algoritmo inverso 7n + 1 (hacia la derecha o hacia la izquierda, según el caso) <br /> <br />379730-635Teorema: Ningún número de formas disminuido en 1 es múltiplo de 7. Similar para Demostración Corolarios: El menor múltiplo de 7 que desciende a 1 al aplicarle el algoritmo 7n +1 es 329. (Vea grafo 7n + 1) No todo natural desciende a 1 al aplicarse el algoritmo 7n + 1. 365 653 53600Teorema: Ningún número de formas disminuido en 1 es múltiplo de 7. Similar para Demostración Corolarios: El menor múltiplo de 7 que desciende a 1 al aplicarle el algoritmo 7n +1 es 329. (Vea grafo 7n + 1) No todo natural desciende a 1 al aplicarse el algoritmo 7n + 1. 365 653 536<br />