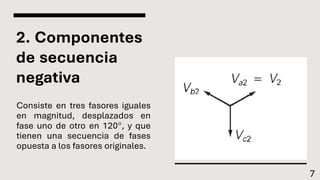
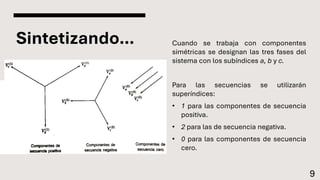
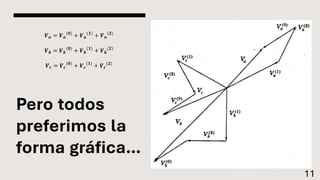
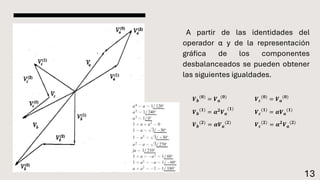
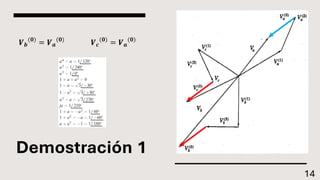
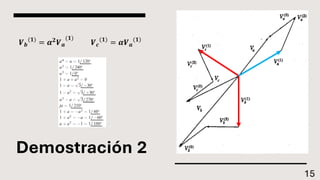
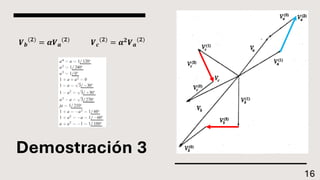
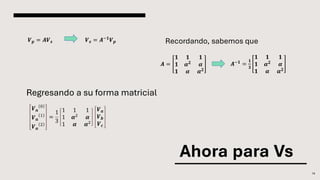
El documento explica el método de componentes simétricas desarrollado por Fortescue para analizar sistemas trifásicos desbalanceados. Este método permite descomponer voltajes y corrientes desbalanceadas en tres conjuntos de componentes balanceados llamados componentes de secuencia positiva, negativa y cero. Las componentes simétricas son útiles para el análisis de fallas asimétricas comunes en sistemas de potencia.

1. Componentes
Simétricas
Daniel Gómez Espinoza Macías
1

2. ¿Qué son las
componentes
simétricas?
Es un método desarrollado por Fortescue para
analizar operaciones desbalanceadas mediante la
transformación de voltajes (y corrientes) trifásicos
desbalanceados en tres conjuntos de voltajes (y
corrientes) balanceados llamados componentes
simétricos.
2

3. Pero primero… ¿es
realmente necesario?
Un desbalance en el sistema puede ser resultado de
un sistema que estaba balanceado, pero tuvo una
falla asimétrica, por ejemplo, una falla de línea a tierra
o de línea a línea.
Este tipo de fallas se presentan con mayor frecuencia
que la falla simétrica (trifásica). En la Tabla 1 se
describen las distintas clases de falla en un sistema
de potencia con sus respectivas frecuencias de
ocurrencia.
3
Tipo de falla
Frecuencia
de
ocurrencia
Fallas
trifásicas (3L)
5%
Fallas de doble
línea a tierra
(LLG)
10%
Falla de doble
línea (LL)
15%
Fallas de una
línea a tierra
(LG)
70%

4. ¿Por qué se
presentan estas
fallas?
• Cuando hay presencia de cargas
desbalanceadas.
• Cuando existen grandes cargas
monofásicas.
En un sistema trifásico que está
normalmente balanceado, los
desbalances ocasionados por una falla
ocasionan, por lo general, que haya
corrientes y voltajes desbalanceados en
cada una de las tres fases.
4

5. Ahora sí, entrando
en materia…
Según el teorema de Fortescue, tres fasores
desbalanceados de un sistema trifásico se pueden
descomponer en tres sistemas balanceados de
fasores.
Los conjuntos balanceados de componentes son…
5

6. 1. Componentes de
secuencia positiva
Consiste en tres fasores
de igual magnitud
desplazados uno del otro
por una fase de 120° y
que tienen la misma
secuencia de fase que los
fasores originales.
6

7. 2. Componentes
de secuencia
negativa
Consiste en tres fasores iguales
en magnitud, desplazados en
fase uno de otro en 120°, y que
tienen una secuencia de fases
opuesta a los fasores originales.
7

8. 3. Componentes de
secuencia cero
Consisten en tres fasores
iguales en magnitud y con un
desplazamiento de fase cero
uno del otro.
8

9. Sintetizando… Cuando se trabaja con componentes
simétricas se designan las tres fases del
sistema con los subíndices a, b y c.
Para las secuencias se utilizarán
superíndices:
• 1 para las componentes de secuencia
positiva.
• 2 para las de secuencia negativa.
• 0 para las componentes de secuencia
cero.
9

10. Matemáticamente
también se puede
Cada uno de los fasores
desbalanceados (Va, Vb, Vc) se
puede expresar en términos
de sus componentes, siendo
la suma de éstos.
10
𝑽𝒂 = 𝑽𝒂
(𝟎)
+ 𝑽𝒂
(𝟏)
+ 𝑽𝒂
(𝟐)
𝑽𝒃 = 𝑽𝒃
(𝟎)
+ 𝑽𝒃
(𝟏)
+ 𝑽𝒃
(𝟐)
𝑽𝒄 = 𝑽𝒄
(𝟎)
+ 𝑽𝒄
(𝟏)
+ 𝑽𝒄
(𝟐)

11. Pero todos
preferimos la
forma gráfica…
11
𝑽𝒂 = 𝑽𝒂
(𝟎)
+ 𝑽𝒂
(𝟏)
+ 𝑽𝒂
(𝟐)
𝑽𝒃 = 𝑽𝒃
(𝟎)
+ 𝑽𝒃
(𝟏)
+ 𝑽𝒃
(𝟐)
𝑽𝒄 = 𝑽𝒄
(𝟎)
+ 𝑽𝒄
(𝟏)
+ 𝑽𝒄
(𝟐)

12. Pequeño
paréntesis
Cuando se trabaja con componentes
simétricas se hace uso de un operador α el
cual es un número complejo que se define
como: 𝛼 = 1∠120°, dicho operador cumple
con ciertas identidades, las cuales se
enlistan la tabla de la izquierda.
12

13. A partir de las identidades del
operador α y de la representación
gráfica de los componentes
desbalanceados se pueden obtener
las siguientes igualdades.
𝑽𝒃
(𝟎)
= 𝑽𝒂
(𝟎)
𝑽𝒄
(𝟎)
= 𝑽𝒂
(𝟎)
𝑽𝒃
(𝟏)
= 𝜶𝟐
𝑽𝒂
(𝟏)
𝑽𝒄
(𝟏)
= 𝜶𝑽𝒂
(𝟏)
𝑽𝒃
(𝟐)
= 𝜶𝑽𝒂
(𝟐)
𝑽𝒄
(𝟐)
= 𝜶𝟐
𝑽𝒂
(𝟐)
13

14. Demostración 1
𝑽𝒃
(𝟎)
= 𝑽𝒂
(𝟎)
𝑽𝒄
(𝟎)
= 𝑽𝒂
(𝟎)
14

15. Demostración 2
𝑽𝒃
(𝟏)
= 𝜶𝟐𝑽𝒂
(𝟏)
𝑽𝒄
(𝟏)
= 𝜶𝑽𝒂
(𝟏)
15

16. Demostración 3
𝑽𝒃
(𝟐)
= 𝜶𝑽𝒂
(𝟐)
𝑽𝒄
(𝟐)
= 𝜶𝟐𝑽𝒂
(𝟐)
16

17. Sustituimos…
Para obtener cada
componente
desbalanceada en función
de una sola variable
17
𝑽𝒂 = 𝑽𝒂
(𝟎)
+ 𝑽𝒂
(𝟏)
+ 𝑽𝒂
(𝟐)
𝑽𝒃 = 𝑽𝒂
(𝟎)
+ 𝜶𝟐𝑽𝒂
(𝟏)
+ 𝜶𝑽𝒂
(𝟐)
𝑽𝒄 = 𝑽𝒂
(𝟎)
+ 𝜶𝑽𝒂
(𝟏)
+ 𝜶𝟐𝑽𝒄
(𝟐)
𝑽𝒂
𝑽𝒃
𝑽𝒄
=
1 1 1
1 𝜶2
𝜶
1 𝜶 𝜶2
𝑽𝒂
0
𝑽𝒂
1
𝑽𝒂
2
𝑽𝒑 = 𝑨𝑽𝒔
Donde Vp es el vector de los
fasores iniciales, Vs es el vector
de componentes simétricos y A
es la matriz de coeficientes

18. Ahora para Vs
Recordando, sabemos que
18
𝑨 =
𝟏 𝟏 𝟏
𝟏 𝜶𝟐 𝜶
𝟏 𝜶 𝜶𝟐
𝑽𝒑 = 𝑨𝑽𝒔 𝑽𝒔 = 𝑨−𝟏𝑽𝒑
𝑨−𝟏
=
𝟏
𝟑
𝟏 𝟏 𝟏
𝟏 𝜶𝟐
𝜶
𝟏 𝜶 𝜶𝟐
𝑽𝒂
0
𝑽𝒂
1
𝑽𝒂
2
=
1
3
1 1 1
1 𝜶2 𝜶
1 𝜶 𝜶2
𝑽𝒂
𝑽𝒃
𝑽𝒄
Regresando a su forma matricial

19. ¡Componentes
simétricas!
Así se llega a la demostración de
cómo descomponer tres factores
asimétricos en sus componentes
simétricas.
Si escribimos la matriz en
ecuaciones separadas y expandidas
obtenemos las siguientes
expresiones
19
𝑽𝒂
(𝟎)
=
𝟏
𝟑
𝑽𝒂 + 𝑽𝒃 + 𝑽𝒄
𝑽𝒂
(𝟏)
=
𝟏
𝟑
𝑽𝒂 + 𝜶𝑽𝒃 + 𝜶𝟐
𝑽𝒄
𝑽𝒂
(𝟐)
=
𝟏
𝟑
𝑽𝒂 + 𝜶𝟐
𝑽𝒃 + 𝜶𝑽𝒄
Siguiendo la misma línea, podríamos
obtener las componentes Vb
(0)
,
Vb
(1)
, Vb
(2)
, Vc
(0)
, Vc
(1)
, Vc
(2)
en caso
de ser necesario

20. ¿Y la corriente?
Las ecuaciones anteriormente
deducidas son fundamentales,
por lo que también se obtendrán
las mismas expresiones pero
ahora para la corriente.
20
𝑰𝒂 = 𝑰𝒂
(𝟎)
+ 𝑰𝒂
(𝟏)
+ 𝑰𝒂
(𝟐)
𝑰𝒃 = 𝑰𝒂
(𝟎)
+ 𝜶𝟐
𝑰𝒂
(𝟏)
+ 𝜶𝑰𝒂
(𝟐)
𝑰𝒄 = 𝑰𝒂
(𝟎)
+ 𝜶𝑰𝒂
(𝟏)
+ 𝜶𝟐𝑰𝒄
(𝟐)
𝑰𝒂
(𝟎)
=
𝟏
𝟑
𝑰𝒂 + 𝑰𝒃 + 𝑰𝒄
𝑰𝒂
(𝟏)
=
𝟏
𝟑
𝑰𝒂 + 𝜶𝑰𝒃 + 𝜶𝟐 𝑰𝒄
𝑰𝒂
(𝟐)
=
𝟏
𝟑
𝑰𝒂 + 𝜶𝟐
𝑰𝒃 + 𝜶𝑰𝒄

21. Otras características
trifásicas
Como la suma de los fasores de voltaje
línea a línea en un sistema trifásico es
siempre cero, las componentes de
secuencia cero nunca estarán presentes
en los voltajes de línea,
independientemente del grado de
desbalanceo.
21
𝑽𝒂𝒃
(𝟎)
=
𝟏
𝟑
𝑽𝒂𝒃 + 𝑽𝒃𝒄 + 𝑽𝒄𝒂 = 𝟎
Por otra parte, la suma de los
voltajes de fase puede no ser
cero, por lo que puede existir
su componente Va
(0)
, de
secuencia cero.

22. Características
de la corriente
Como la suma de las tres
corrientes de línea es igual a la
corriente en el conductor neutro,
entonces la corriente en el neutro es
tres veces la corriente de línea de
secuencia cero.
𝑰𝒂
(𝟎)
=
𝟏
𝟑
𝑰𝒂 + 𝑰𝒃 + 𝑰𝒄 =
𝟏
𝟑
𝑰𝒏
22
𝑰𝒂
(𝟎)
=
𝟏
𝟑
𝑰𝒏 = 𝟎
Si la conexión del neutro es
eliminada la corriente de línea de
secuencia cero siempre es cero.

23. Referencias
[1] J.J. Grainer., W. D. Stevenson. “Componentes
simétricas y redes de secuencia”, en Análisis de
Sistemas de Potencia, McGraw Hill, pp 391-396
[2] D.P. Kothari. I.J. Nagrath,,”Componentes
Simétricos”, en Sistemas Eléctricos de Potencia,
3ra ed, McGraw Hill, pp 369-376.
[3] J. Duncan Glover. M. S. Sarma. T. J. Overbye,
“Symmetrical Components”, en Power Systems,
5ta edición, Cengeage Learning, pp 428-432
23