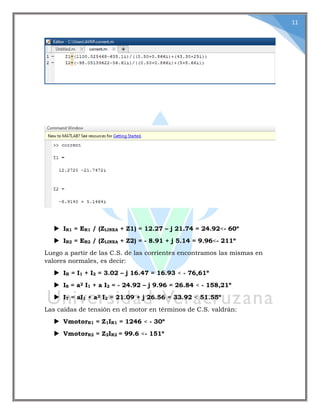
Este documento presenta el análisis de componentes simétricas para sistemas trifásicos desequilibrados. Introduce el método de componentes simétricas desarrollado por C.L. Fortescue en 1918 que permite descomponer un sistema trifásico desequilibrado en tres sistemas equilibrados llamados secuencia positiva, negativa y nula. Explica cómo resolver problemas de componentes simétricas utilizando el programa MATLAB, mostrando ejemplos numéricos de cálculo de corrientes y tensiones en componentes simétricas para un

1. 25-5-2016 COMPONENTES
SIMETRICAS
Materia: Corto circuito y flujo de carga
PROFESOR: ALFREDO GONZALES FUENTEVILLA
INTEGRANTES:
GARCIA CABRERA IDELFONSO DE JESUS
NUÑEZ ACUÑA CECILIA
ROJAS RODRIGUEZ DAVID
VICENCIO MENDOZA ALEJANDRO
ESCUELA: UNIVERSIDAD VERACRUZANA CAMPUS
COATZACOALCOS
COATZACOALCOS, VERACRUZ

2. 1
CONTENIDO
INTRODUCCIÓN ..................................................................................................2
ANTECEDENTES .................................................................................................3
PROBLEMA..........................................................................................................7
OBJETIVO ...........................................................................................................8
JUSTIFICACIÓN...................................................................................................8
HIPOTESIS ..........................................................................................................8
METODOLOGÍA ...................................................................................................9
IMPACTO AMBIENTAL .......................................................................................15
CONCLUSIÓN ....................................................................................................15
RECOMENDACIONES........................................................................................15

3. 2
INTRODUCCIÓN
Hace tiempo se discutía entre dos tipos de corriente las cuales eran:
 Corriente directa la cual era defendida por el inventor Tomas Alba
Edison
 Corriente alterna que había sido descubierta por Nikola Tesla
Con el tiempo se demostró que la corriente alterna era mucho más
eficiente y económica.
En la actualidad tenemos sistemas monofásicos y trifásicos los cuales
hacen la vida un poco más fácil pero para las industrias son los sistemas
trifásicos. Para abastecer estos lugares se requieren de sistemas de
potencia trifásicos simétricos.
En ocasiones, el sistema de potencia se ve expuesto a ciertos estados de
operación que producen desbalances en el sistema; como las cargas
asimétricas y las fallas asimétricas.
En el sistema de potencia, el análisis de las condiciones de operación
desbalanceada, ha sido especialmente simplificado gracias a la aplicación
de un artificio matemático, el cual permite la condición de desbalance sea
estudiada en forma balanceada. Este particular método recibe el nombre
de Componentes Simétricas.

4. 3
ANTECEDENTES
En los métodos antiguos de análisis de sistemas de potencia, se era
necesario asignar símbolos a las cantidades en las tres fases y resolver el
sistema como un todo, resultando complicado, hasta con la utilización de
computadores digitales.
En el año de 1918, durante una reunión del "American Institute of Electric
Engineers" (actual Institute of Electric and Electronic Engineers, IEEE), el
investigador C. L. Fortescue, presentó un trabajo que hoy por hoy
constituye una de las más poderosas herramientas para el estudio de
sistemas polifásicos desequilibrados.
FORTESCUE ESTABLECE:
El trabajo de Fortescue establece que un conjunto de n fasores
desbalanceados puede expresarse como n-1 sistemas de n fasores
equilibrados de la n secuencias posibles y un sistema particular de fasores
sin fase alguna.

5. 4
Por lo tanto se puede establecer la siguiente ecuación:
Para realizar el estudio analítico de las componentes simétricas vamos a
definir el operador “a” o de avance trifásico, que va a permitirnos relacionar
entre sí los vectores de cualquier sistema h, d, i. El operador a es un vector
unitario de módulo la unidad y argumento 120º. Normalmente no se indica
expresamente su carácter vectorial. Su aplicación implica un giro de 120º;
es un vector similar a j, cuya aplicación producía un giro de 90º. Vamos a
ver algunos valores de su aplicación.
Este factor de fase a, posee algunas propiedades
a=1<120°
1+ a + a2 = 0
1+ a3 + a3 = 3
a3 = 1; a4 = a; a5 = a2

6. 5
Determinación de las componentes simétricas
La determinación de las componentes simétricas de una sistema
desequilibrado de fasores puede hacerse de dos formas: analítica o
gráficamente, ambas formas se basan en los fasores originales y
solamente se apunta el cálculo hacia la determinación de las componentes
de un solo fasor original, por costumbre la fase “a”, ya que mediante el
operador “a” y las propiedades del mismo, quedarán determinados los
fasores que compondrán las distintas fases.
SECUENCIA POSITIVA
Si el sistema original posee secuencia a-b-c, este poseerá la misma
secuencia. Como esta es perfecta solo será necesario determinar el módulo
y fase de uno de los fasores, en función de los fasores originales, para ello
recurrimos al operador “a”, antes definido. La terna de secuencia directa
queda identificada con:
 Ia1 = | Ia1 | < 0º
 Ib1 = a2 Ia1 = | Ia1 | < - 120º
 Ic1 = a Ia1 = | Ia1 | < 120º
SECUENCIA NEGATIVA
Si el sistema original posee secuencia a-b-c, esta terna poseerá una
secuencia de fases a-c-b y quedará expresada por:
 Ia2 = | Ia2 | < 0º
 Ib2 = a Ia2 = | Ia2 | < 120º
 Ic2 = a2 Ia2 = | Ia2 | < - 120º
SECUENCIA NULA
En este caso los tres fasores forman un sistema monofásico de manera tal
que:
 Ia0 = Ib0 = Ic0 = I0
Para que se cumpla el teorema de Fortescue, debe satisfacerse que:
 Ia = Ia0 + Ia1 + Ia2
 Ib= Ib0 + Ib1 + Ib2 = Ia0 + a2Ia1 + aIa2

7. 6
 Ic = Ic0 + Ic1 + Ic2 = Ia0 + a Ia1 + a2Ia2
El método algebraico evoluciona con operaciones que propenden a obtener
la expresión 1+ a2 + a, que es igual a cero.
Por ejemplo el término:
 Ib = Ia0 + a2Ia1 + aIa2 lo multiplicamos por “a” resultará:
 aIb = a Ia0 + a3Ia1 + a2Ia2 dado que a3 = 1 <0º será:
 aIb = aIa0 + Ia1 + a2Ia2
Lo expresado por la expresión es una operación de rotación en 120º del
fasor original perteneciente a la fase "b". Si ahora se efectúa la rotación de
la fase "c" en 240º o sea hacemos:
 a2Ic = a2Ia0 + a3Ia1 + a4Ia2
 a2Ic = a2Ia0 + Ia1 + aIa2
Efectuando la suma de las ecuaciones resultará:
 Ia = Ia0 + Ia1 + Ia2
 aIb = aIa0 + Ia1 + a2Ia2
 a2Ic = a2Ia0 + Ia1 + aIa2
Ia + aIb + a2 Ic = 3Ia1
El fasor básico de la secuencia "2" [Ia2] puede ser hallado mediante un
proceso análogo al anterior, se tratará en este caso de eliminar los
términos Ia1 y Ia0 y retener los términos Ia2 del sistema.
Esto se logra multiplicando por “a2” ambos miembros de la segunda
ecuación del sistema y por “a” ambos miembros de la tercera ecuación del
sistema anterior:
 Ia = Ia0 + Ia1 + Ia2
 a2Ib = a2 Ia0 + a4 Ia1 + a3 Ia2
 aIc = a Ia0 + a2 Ia1 + a3 Ia2
 Ia + a2 Ib + a Ic = (1+2a3) Ia2
 Ia + a2 Ib + a Ic = 3 Ia2
El fasor básico de la secuencia nula [Ia0], se obtendrá por la suma directa
de las ecuaciones del sistema, será:

8. 7
 Ia = Ia0 + Ia1 + Ia2
 Ib = Ia0 + a2 Ia1 + aIa2 [13]
 Ic = Ia0 + aIa1 + a2Ia2
 Luego resulta: Ia + Ib + Ic = 3Ia0
Si resumimos las expresiones que determinan las componentes simétricas
serán:
 Ia0 = 1/3 (Ia + Ib + Ic)
 Ia1 = 1/3 (Ia + aIb + a2Ic)
 Ia2 = 1/3 (Ia + a2Ib + aIc)
De forma matricial
Ia0 1 1 1 Ia
Ia1 1/3 1 a a2 Ib
Ia2 1 a2 a Ic
PROBLEMA
Un sistema polifásico desequilibrado se puede estudiar directamente
aplicando las leyes de Kirchhoff a la red. No obstante este procedimiento de
cálculo directo es laborioso, al tener que trabajar con un gran número de
ecuaciones. Las tensiones, intensidades o impedancias están representadas
por magnitudes vectoriales complejas, por lo que el número de ecuaciones
se duplica, complicando aún más su resolución.
¿Será posible facilitar la resolución de las operaciones del problema?

9. 8
OBJETIVO
Resolver mediante un programa especializado los problemas que un
ingeniero electricista se enfrenta al resolver en la vida cotidiana sobre las
componentes simétricas para un sistema trifásico.
OBJETIVOS ESPECIFICOS
 Mostrar y explicar los pasos y comandos a seguir para la resolución
de problemas de componentes simétricas en el programa MATLAB.
 Escribir el código de programación en MATLAB.
JUSTIFICACIÓN
La razón principal de este trabajo se debe a que la complejidad de los
problemas de componentes simétricas es arduo y exhausto y se quiere dar
a conocer nuevas tecnologías y programas que ayuden a la solución de los
problemas. Además de dar a entender que puede ser una alternativa para
preservar el medio ambiente previniendo algunos sucesos y dar a entender
que la tecnología no solo daña al ambiente.
HIPOTESIS
Se cree que al no tener conocimiento acerca de programas que pueden
resolver estas operaciones con facilidad se piensa que los métodos de
solución son complicados.

10. 9
METODOLOGÍA
Método de las componentes simétricas” se aplica a la resolución de redes
polifásicas, para soluciones analíticas de redes. Sirve para cualquier
sistema polifásico desequilibrado: en el cual n fasores relacionados entre sí
pueden descomponerse en n sistemas de vectores equilibrados
(componentes simétricos).
MATLAB ("laboratorio de matrices") es una herramienta de software
matemático que ofrece un entorno de desarrollo integrado con un lenguaje
de programación propio (lenguaje M).
Entre sus prestaciones básicas se hallan: la manipulación de matrices, la
representación de datos y funciones, la implementación de algoritmos, la
creación de interfaces de usuario y la comunicación con programas en
otros lenguajes y con otros dispositivos hardware.
COMANDOS BASICOS
 * símbolo utilizado para realizar una multiplicación
 / este símbolo se utiliza para realizar alguna división
 = con este signo permitirá a que será igual la variable que queremos
conocer
 i cuando una variable o numero esta acompañado de esta literal se
indica que hablaremos de números complejos
 () los paréntesis ayudarán a indicar el orden jerárquico de las
operaciones a realizar
Ejemplo:
Un motor de inducción trifásico conectado en estrella tiene una
impedancia por fase de 43,30 + j 25 a las corrientes de secuencia positiva
y una impedancia de 5,00 + j 8,66 por fase a corrientes de secuencia
negativa cuando están alimentando una carga mecánica determinada. El
motor recibe energía de una línea trifásica que tiene una impedancia de
0,50 + j 0,866 W por conductor. El motor no tiene neutro. Las tensiones
entre fases en la fuente son:
ERS = 2000 < 0º ; EST = 2300 <-115,77º ; ETR = 2300 < 115,77º
a) ¿Cuáles son las corrientes de secuencia positiva y negativa, tomando
ERS como eje de referencia?
b) ¿Cuáles son las tensiones de secuencia positiva y negativa en bornes del
motor?

11. 10
Resolución: Como primer paso encontraremos las C.S. de las tensiones
compuestas desequilibradas aplicadas, tomando como referencia la
tensión 𝐸 𝑅𝑆, es decir: 𝐸 𝑅𝑆 = 2000 < 0º ; 𝐸𝑆𝑇 = 2300 <-115,77º ; 𝐸 𝑇𝑅 = 2300
<115,77º
Dado que los sistemas simétricos de secuencia 1 y 2 constituyen sistemas
perfectos se cumple que la relación entre una tensión compuesta y una
simple es √3 en lo que respecta al módulo y existe un desfasaje de 30º, en
atraso o adelanto, según se considere la secuencia 1 o secuencia 2, por lo
tanto:
 ERS1 = 2197,14<0º ER1 = 2197,14/√𝟑 < - 30º = 1270,2 < (0º-
30º)
 ERS2 = - 195,87/√𝟑 = 195,87/√𝟑 <180º ER2 = 113,22 < (180º
+30º)
Luego, conociendo las tensiones simples en C.S. aplicaremos la 2º Ley de
Kirchhoff para cada secuencia para encontrar las corrientes en términos
de C.S., a saber:

12. 11
 IR1 = ER1 / (ZLINEA + Z1) = 12.27 – j 21.74 = 24.92<- 60º
 IR2 = ER2 / (ZLINEA + Z2) = - 8.91 + j 5.14 = 9.96<- 211º
Luego a partir de las C.S. de las corrientes encontramos las mismas en
valores normales, es decir:
 IR = I1 + I2 = 3.02 – j 16.47 = 16.93 < - 76,61º
 IS = a2 I1 + a I2 = - 24.92 – j 9.96 = 26.84 < - 158,21º
 IT = aI1 + a2 I2 = 21.09 + j 26.56 = 33.92 < 51.55º
Las caídas de tensión en el motor en términos de C.S. valdrán:
 VmotorR1 = Z1IR1 = 1246 < - 30º
 VmotorR2 = Z2IR2 = 99.6 <- 151º

13. 12
EJEMPLO 2
Tres resistencias idénticas conectadas en Y forman un banco de carga con
valores nominales de 2300 V y 500 kVA. Encuentre los voltajes de línea y
las corrientes en por unidad en la carga si se aplican al banco de carga los
voltajes
|Vab| = 1840 V |Vbc| = 2760 V |Vca| = 2300 V
Suponga que el neutro de la carga no esta conectado al neutro del sistema
y selecciones una base de 2300 V y 500 kVA.
Los valores nominales del banco de carga coinciden con las bases
específicas y así los valores de las resistencias son de 1.0 por unidad.
Sobre la misma base, los voltajes de líneas dados en por unidad son
|Vab| = 1840 V
2300 V
= 0.8 |Vbc| = 2760 V
2300 V
= 1.2 |Vca| = 2300 V
2300 V
= 1
Si se supone un ángulo de 180° para Vca y se aplica la ley de cosenos para
encontrar los ángulos de los demás voltajes de línea se obtienen los
siguientes valores en por unidad
𝑉𝑎𝑏
2
= 𝑉𝑏𝑐
2
+ 𝑉𝑐𝑎
2
− 2𝑉𝑏𝑐 𝑉𝑐𝑎 𝑐𝑜𝑠𝛼
𝛼 = cos−1
𝑉𝑎𝑏
2
− 𝑉𝑏𝑐
2
− 𝑉𝑐 𝑎
2
−2𝑉𝑏𝑐 𝑉𝑐 𝑎
𝛼 = cos−1
0.82
− 1.22
− 12
−2(1.2)(1)
𝛼 = 41.4°
𝑉𝑏𝑐
2
= 𝑉𝑎𝑏
2
+ 𝑉𝑐 𝑎
2
− 2𝑉𝑎𝑏 𝑉𝑐 𝑎 𝑐𝑜𝑠𝛽
𝛽 = cos−1
𝑉𝑏𝑐
2
− 𝑉𝑎𝑏
2
− 𝑉𝑐𝑎
2
−2𝑉𝑎𝑏 𝑉𝑐 𝑎
𝛽 = cos−1
0.82
− 1.22
− 12
−2(1.2)(1)
𝛽 = 82.8°

14. 13
𝑉𝑎𝑏 = 0.8∠82.8°
𝑉𝑏𝑐 = 1.2∠ − 41.4°
𝑉𝑐 𝑎 = 1∠180°
𝑉𝑎𝑏
(1)
=
1
3
(0.8∠82.8° + 1.2∠120° − 41.4° + 1∠240° + 180°)
Vab
(1)
=
1
3
(0.8∠82.8° + 1.2∠78.6° + 1∠420°)
Vab
(1)
=
1
3
(0.1003 + j0.7937 + 0.2372 + j1.1763 + 0.5 + j0.8660)
Vab
(1)
=
1
3
(0.8375 + j2.836)
Vab
(1)
= 0.2792 + j0.9453
Vab
(1)
= 0.9857∠73.6°
𝑉𝑎𝑏
(2)
=
1
3
(0.8∠82.8° + 1.2∠240° − 41.4° + 1∠120° + 180°)
Vab
(2)
=
1
3
(0.8∠82.8° + 1.2∠198.6° + 1∠300°)
Vab
(2)
=
1
3
(0.1003 + j0.7937 − 1.1373 − j0.3828 + 0.5 − j0.8660)
Vab
(2)
=
1
3
(−0.537 − j0.4551)
Vab
(2)
= −0.1790 − j0.1517
Vab
(2)
= 0.2346∠220.3°
La ausencia de la conexión al neutro implica que no están presentes las
componentes de secuencia cero. Por lo tanto, los voltajes de fase en la carga
contienen solamente componentes de secuencia positiva y negativa. Los
voltajes de fase se encuentran a partir de las siguientes ecuaciones.
𝑉𝑎𝑛
(1)
= 0.9857∠73.6° − 30°
𝑉𝑎𝑛
(1)
= 0.9857∠43.6°
𝑉𝑎𝑛
(2)
= 0.2346∠220.3° + 30°
𝑉𝑎𝑛
(2)
= 0.2346∠250.3°

15. 14
Como cada resistencia tiene una impedancia de 1.0∠0° en por unidad,
𝐼 𝑎
(1)
=
𝑉𝑎
(1)
1.0
= 0.9857∠43.6°
𝐼 𝑎
(2)
=
𝑉𝑎
(2)
1.0
= 0.2346∠250.3°
La dirección positiva de la corriente se selecciona como la que va desde la
fuente hacia la carga

16. 15
IMPACTO AMBIENTAL
En estos días se cree que el avance tecnológico crea cambios negativos en el
medio ambiente, lo ideal sería que todo este avance tecnológico de las
herramientas informáticas tenga un impacto positivo el cual será que los
cálculos sean más fiables y con ello se reduzca los errores humanos al hacer
cálculos manuales.
Con la ayuda de la informática los cálculos serán más precisos y se logrará
que los diseños de equipos y sistemas sean mejores, hablando en términos
más ecológicos los cálculos manuales requieren de papel y lápiz al usar
estas herramientas tan elementales contribuimos a la tala de árboles y esto
a su vez conlleva a un cambio climático o un problema que se vive en estos
días conocido como calentamiento global.
Lo cual nos hace pensar que al seguir utilizando estos programas
ayudaremos a que el medio ambiente no se degrade aún más.
CONCLUSIÓN
Las componentes simétricas son una herramienta poderosa la cual nos
facilita el cálculo de sistemas trifásicos desbalanceados los cuales permiten
descomponer este sistema en tres como son: secuencia cero, secuencia
positiva y secuencia negativa. Al tener esta herramienta matemática le
añadimos una que facilita aún más estos cálculos la cual es la tecnología
informática para ser más específicos software de programación con ello
podemos resolver problemas de una manera más eficiente a su vez
preservando el medio ambiente como se mencionó anteriormente.
RECOMENDACIONES
Esta tecnología puede volverse más eficiente al crear un algoritmo o script
el cual solo te pida las variables conocidas dando de alta el operador “a” con
ello que el programa vea la lógica a seguir que estará basada en las 3 leyes
básicas de la electricidad las cuales son Ley de ohm, ley de corrientes de
Kirchhoff y ley de tensiones de Kirchhoff así será un programa con una
lógica enfocada a la ingeniería eléctrica.