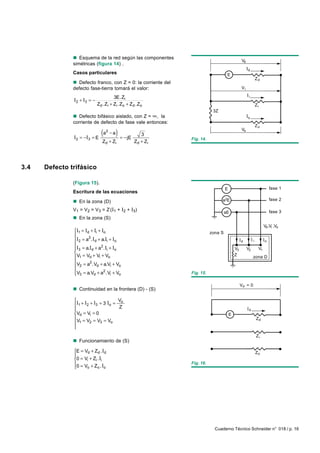
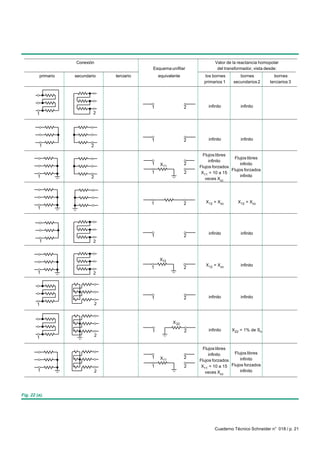
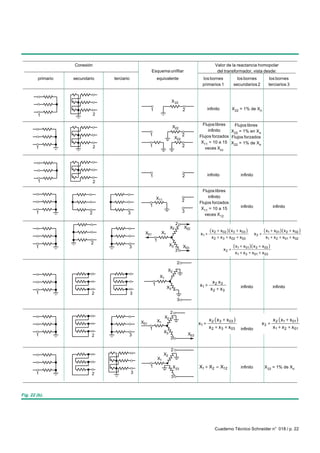
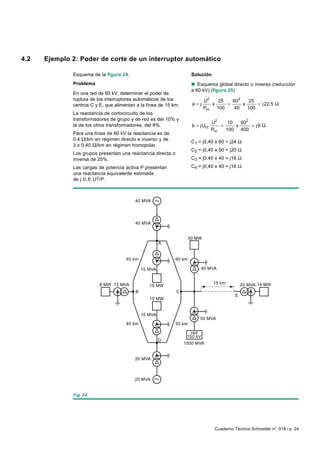
Este documento presenta el análisis de redes eléctricas trifásicas en condiciones perturbadas utilizando el método de las componentes simétricas. Primero repasa conceptos matemáticos de vectores y componentes simétricas. Luego aplica este método para calcular parámetros en diferentes tipos de cortocircuito como defecto fase-tierra, defecto bifásico a tierra, defecto trifásico y redes con cargas desequilibradas. Finalmente incluye ejemplos numéricos resueltos.

1. Cuaderno Técnico nº 018
Análisis de las redes trifásicas en
régimen perturbado con la ayuda
de las componentes simétricas
Benoit de Metz-Noblat

2. La Biblioteca Técnica constituye una colección de títulos que recogen las novedades electrotécnicas
y electrónicas. Están destinados a Ingenieros y Técnicos que precisen una información específica o
más amplia, que complemente la de los catálogos, guías de producto o noticias técnicas.
Estos documentos ayudan a conocer mejor los fenómenos que se presentan en las instalaciones, los
sistemas y equipos eléctricos. Cada uno trata en profundidad un tema concreto del campo de las
redes eléctricas, protecciones, control y mando y de los automatismos industriales.
Puede accederse a estas publicaciones en Internet:
http://www.schneiderelectric.es
Igualmente pueden solicitarse ejemplares en cualquier delegación comercial de Schneider Electric
España S.A., o bien dirigirse a:
Centro de Formación Schneider
C/ Miquel i Badia, 8 bajos
08024 Barcelona
Telf. (93) 285 35 80
Fax: (93) 219 64 40
e-mail: formacion@schneiderelectric.es
La colección de Cuadernos Técnicos forma parte de la «Biblioteca Técnica» de Schneider Electric
España S.A.
Advertencia
Los autores declinan toda responsabilidad derivada de la incorrecta utilización de las informaciones y esquemas
reproducidos en la presente obra y no serán responsables de eventuales errores u omisiones, ni de las consecuencias
de la aplicación de las informaciones o esquemas contenidos en la presente edición.
La reproducción total o parcial de este Cuaderno Técnico está autorizada haciendo la mención obligatoria:
«Reproducción del Cuaderno Técnico nº 018 de Schneider Electric».

3. Cuaderno Técnico no 018
Análisis de las redes trifásicas en
régimen perturbado con la ayuda de las
componentes simétricas
Benoit de METZ-NOBLAT
Ingeniero ESE, trabajó en Saint Gobain como
Ingeniero de investigación y después en la sección
de pruebas y equipos nuevos en una empresa de
producción.
Entró en Merlin Gerin en 1 986, trabajando como
Ingeniero en el servicio de estudios de redes,
especializándose en el estudio de las
sobretensiones, armónicos y la estabilidad dinámica
de las redes.
Trad.: E. Milà; J.M. Giró
Original francés: diciembre 1 990
Versión española: marzo 2 000

4. Análisis de las redes trifásicas en régimen
perturbado con la ayuda de las
componentes simétricas
La determinación de las dimensiones de una instalación y los materiales que la
componen, la regulación de las protecciones y el análisis de los fenómenos
eléctricos precisan, a menudo, el cálculo de las corrientes y las tensiones
presentes en las redes.
El desarrollo de este Cuaderno Técnico persigue, como finalidad primordial, la
presentación o recordatorio de un método simple de cálculo (con la ayuda de las
componentes simétricas) de todos los parámetros en las redes trifásicas en
régimen perturbado.
1 Presentación p. 5
2 Repaso matemático de la 2.1 Representación vectorial de un fenómeno físico p. 6
teoría de vectores 2.2 Definición de base p. 6
2.3 Representación vectorial p. 7
2.4 Componentes simétricas p. 8
2.5 Descomposición de un sistema trifásico en p. 9
sus componentes simétricas
2.6 Cálculo de las componentes simétricas p. 10
2.7 Conclusión: aplicación a la electrotecnia p. 11
3 Aplicaciones elementales 3.1 Método de cálculo de los regímenes desequilibrados p. 12
3.2 Defecto fase-tierra (llamado defecto homopolar) p. 13
3.3 Defecto bifásico a tierra p. 15
3.4 Defecto trifásico p. 16
3.5 Red con cargas desequilibradas p. 17
3.6 Impedancias asociadas a las componentes simétricas p. 18
3.7 Formulario de recapitulación p. 20
4 Ejemplos resueltos 4.1 Ejemplo 1: Poder de corte de un interruptor automático p. 23
4.2 Ejemplo 2: Poder de corte de un interruptor automático p. 24
4.3 Ejemplo 3: Regulación de protecciones homopolares en una p. 28
red MT con neutro a tierra
4.4 Ejemplo 4: Medición de las componentes simétricas de p. 30
un sistema de tensión y de corriente
Cuaderno Técnico Schneider n° 018 / p. 4

5. 1 Presentación
Si consideramos el funcionamiento en régimen El método general, aplicando de las leyes de
normal equilibrado simétrico, el estudio de las Ohm y de Kirchhoff, es posible, pero resulta
redes trifásicas puede reducirse al estudio de largo y complicado.
una red monofásica equivalente de tensiones El método de las componentes simétricas,
iguales a las tensiones simples de la red, de descrito en el presente documento, simplifica
corrientes iguales a las de la red e impedancias los cálculos y permite una solución mucho más
iguales a las de la red, denominadas fácil que la superposición de tres redes
impedancias cíclicas. monofásicas independientes. Después de
Al aparecer una asimetría significativa en la repasar las nociones vectoriales, se aplica este
configuración de la red, ya no es posible aplicar método a los diferentes tipos de cortocircuito,
la simplificación, pues no podemos establecer acabando con unos ejemplos de casos
las relaciones entre los diferentes conductores prácticos reales.
con la ayuda de una impedancia cíclica para
cada elemento de la red.
Cuaderno Técnico Schneider n° 018 / p. 5

6. 2 Repaso matemático de la teoría de vectores
2.1 Representación vectorial de un fenómeno físico
Un fenómeno físico vibratorio es senoidal n Recíprocamente, se puede hacer
cuando la elongación de un punto vibrante es corresponder un vector giratorio a cualquier
una función senoidal del tiempo función senoidal
x = a cos (ωt + ϕ) x = a cos (ωt + ϕ).
Esta aplicación es perfectamente conocida en Por convenio, se representa la función x por el
uuuu
r
electrotecnia, donde tanto corrientes como vector OM en la posición que ocupa en el
tensiones son fenómenos senoidales. instante inicial t = 0; el módulo del vector
uuuu
r representa lauuu uuuu
amplitud, a, de la función senoidal,
n Consideremos un vector uuu de módulo a, r r
(
uuu OM
r r
)
girando sobre el plano Ox, Oy alrededor de su ( )
y el ángulo Ox, OM representa su fase inicial.
origen O con una velocidad angular constante ω n Por tanto, el estudio de un fenómeno físico
(figura 1). senoidal puede reducirse al estudio del vector
uuu uuuu
r r
(
Si en el instante inicial t = 0, el ángulo Ox, OM ) que le corresponde, lo que es muy interesante,
porque la utilización matemática de los vectores
tiene un valor ϕ, en el instante t, tendrá un valor
(ωt + ϕ). es accesible. Se aplica en particular al dominio
uuuu
r de los fenómenos eléctricos trifásicos en los que
Proyectamos el vector corriente OM sobre el eje
uuu
r las tensiones y corrientes están representadas
Ox . El valor algebraico de esta proyección es, por vectores giratorios.
en el instante t
x = a cos (ωt + ϕ).
Con lo que: y
o el movimiento de la proyección rdel extremo
uuu
del vector giratorio sobre el eje Ox es un M
IaI
movimiento senoidal de amplitud a, igual al t
módulo de este vector, -a O x x
+a
o la pulsación ω del movimiento senoidal es
igual a la velocidad angular del vector giratorio,
o la fase inicial ϕ es igual al uuu
ángulo formado por
r
el vector giratorio con el eje Ox en el Fig. 1.
instante t = 0.
2.2 Definición de base
ur
n Sea un fenómeno eléctrico pulsatorio n El vector V , cuyo origen se sitúa en O, se
senoidal, representado por un vector giratorio
uur caracteriza esencialmente por:
V (figura 2). ur
o una amplitud V : en un instante dado, la
n Se toma previamente sobre el plano: longitud del vector es numéricamente igual al
uuu
r módulo de la amplitud máxima del fenómeno,
o un eje de referencia Ox de vector unitario
uu uu
r r o una fase ϕ: es, en un instante dado, el ángulo
x : x = 1, uuu ur
r ur
( )
Ox, V , que forma V con el eje de referencia
o un sentido de rotación, convencionalmente uuu
r
definido como positivo en el sentido Ox , teniendo en cuenta el sentido de rotación
antihorario + . adoptado.
Cuaderno Técnico Schneider n° 018 / p. 6

7. o una pulsación: es la velocidad de rotación
constante del vector, en radianes por segundo.
Se expresa habitualmente en revoluciones por
segundo y en tal caso da la frecuencia del
fenómeno expresada en Hz (1 Hz = 2 π rad/s). + V
n Un sistema trifásico es un conjunto de 3
→ → →
vectores V1, V2, V3 con origen común, de igual
O
pulsación y que tengan cada uno una amplitud x x
constante.
n Un sistema eléctrico es lineal cuando
presenta proporcionalidad de relación causa-
efecto. Fig. 2.
2.3 Representación vectorial
→
El vector V se representa clásicamente en un
sistema de ejes de coordenadas rectangulares y
+
(figura 3):
ur uuuu uuur uuur
r r r Y M
V = OM = OX + OY = OX. x + OY . y
n Operador «j» V
Para facilitar las operaciones con los vectores,
uur y
V puede representarse de forma equivalente
O x X x
con un número complejo utilizando el
operador «j».
Fig. 3.
«j» es un operador vectorial que consiste en
girar el vector al que se aplicauuu ángulo de
un uu
r r
+ π/2; por tanto, en la figura, jx = y . aV
+
Por tanto, se ve que: 120o
 π 
j2 = −1  rotación de 2 x = π 120o V
 2 
120o
 π 3π 
j = − j  rotación de 3 x
3
= 
 2 2  a2 V
 π 
j4 = +1  rotación de 4 x = 2π  Fig. 4.
 2 
a2 hace girar un vector un ángulo:
de donde:
ur r uu r
r 2π 4π 2π 
(
V = OX. x + OY . j y = x OX + j OY ) 2x
3
=
3

 equivalente a −
 3 
,
n Operador «a» a3 hace girar un vector un ángulo:
«a» es un operador vectorial que consiste en 2π
2π 3x = 2π (equivalente a 0 ) ,
aplicar un giro de + al vector sobre el que 3
3 3 3 ,
a = − 0,5 + j ; a2 = − 0,5 − j
se realiza la operación (figura 4). 2 2
Vemos que:
de donde:
Cuaderno Técnico Schneider n° 018 / p. 7

8. a0 = a3 = a6 ... = 1 Esta última relación se verifica gráficamente
a= a4 = a7 = ... constatando, sobre la figura, que la suma de los
vectores representados es nula:
a= a–2 = a–5 = ... ur ur ur
V + a.V + a2 .V = 0
ur
( )
a2 = a5 = a8 = ...
de donde V 1 + a + a2 = 0 ,
a2 = a–1 = a–4 = ...
y, por tanto:
a − a2 = j 3 1 + a + a2 = 0.
y
1 + a + a2 = 0.
2.4 Componentes simétricas
Sea un conjunto de tres vectores trifásicos n El «sistema inverso», todavía denominado
senoidales que giran a la misma velocidad. Se por los anglosajones «secuencia negativa»
consideran fijos unos respecto a los otros. (figura 6):
uu uur uur
r
Existen tres disposiciones particulares que V1,V2,V3 :
representan una simetría de los vectores entre
sí y que se ha dado en calificarlas como o tienen la misma amplitud,
«componentes simétricas». o están desfasados 120o,
n El «sistema directo», todavía denominado por o están dispuestos de forma que un observador
los anglosajones «secuencia positiva» en reposo vea desfilar los vectores en el orden
uuur uuuu uuuu
r r
(figura 5): V1 , V2 , V3 : uu uur uuu
r r
V1,V3 ,V2;
o tienen la misma amplitud, uur
V1
o están desfasados 120o, uur uur
V2 = a. V1
o están dispuestos de forma que un observador uur uur uur
en reposo vea desfilar los vectores en el orden V3 = a2 .V1 = a. V2 .
uuur uuuu uuuu
r r
V1 , V2 , V3 :
uur
V1
V2
uur uur uur
V2 = a2 .V1 = a. V3 120o
uur uur V1
V3 = a.V1 .
120o
120o
V3
V3
120o
Fig. 6: Sistema inverso.
o
120
V1
120o
V2
Fig. 5: Sistema directo.
Cuaderno Técnico Schneider n° 018 / p. 8

9. n El «sistema homopolar», denominado por los
anglosajones «secuencia nula» (figura 7) V3
uu uur uur
r V2
V1,V2,V3 : V1
o tienen la misma amplitud,
o están en fase y por tanto son colineales; un
observador en reposo los vería pasar al mismo
tiempo. Fig. 7: Sistema homopolar.
2.5 Descomposición de un sistema trifásico en sus componentes simétricas
Sea un sistemar trifásico cualquiera formado por uu uur uu uur
r r
uu uur uur V1 = Vd + Vi + Vo
tres vectores V1,V2 ,V3 (definiciones de base); uur uur uu uur
r
se demuestra que este sistema es la suma de 3 V2 = a2 . Vd + a. Vi + Vo
sistemas trifásicos equilibrados: directo, inverso uur uur uu uur
r
V3 = a. Vd + a2 . Vi + Vo
y homopolar.
uuur uuuu uuuu
r r
Sistema directo: Vd1, Vd2, Vd3 Se pueden calcular las componentes simétricas:
uur uuu uuu
r r
Sistema inverso: Vi1, Vi2, Vi3 uur 1 uu
r uur uur
uuur uuuu uuuu
r
Sistema homopolar: Vo1, Vo2 , Vo3 .
r Vd =
3
( V + a. V
1 2 + a2 . V3 )
uu
r 1 uu
r uur uur
Se verificará que:
Vi =
3
(V + a
1
2
. V2 + a. V3 )
uu uuur uur uuur
r uur 1 uu
r uur uur
V1 = Vd1 + Vi1 + Vo1
uur uuuu uuu uuuu
r r r
Vo =
3
( V1 + V2 + V3 )
V2 = Vd2 + Vi2 + Vo2
uur uuuu uuu uuuu
r r r
V3 = Vd3 + Vi3 + Vo3 La construcción geométrica de las componentes
simétricas se consigue teniendo en cuenta el
Si elegimos los vectores con índice 1 como 2π 
significado del operador «a»  rotación de
 3 
vectores de origen y hacemos intervenir el
 
operador «a» se tiene que:
(figura 8).
O
V2 Vo V3
+ O
V2
O
Vi V2
Vd
V3 120o
V1
aV3
O aV2 V1
V3
V1
uur 1 uu
r uur uur
120o Vo =
3
( V1 + V2 + V3 )
uur 1 uu
r uur uur
Vd =
3
( V + a. V
1 2 + a2 . V3 ) a2 V 2
V1
uu
r 1 uu
r uur uur
(V + a )
Sistema dado
a2 V 3 Vi = 2
. V2 + a. V3
1
3
Fig. 8.
Cuaderno Técnico Schneider n° 018 / p. 9

10. De forma más práctica se pueden construir las baricentro del triángulo ABC; un cálculo sencillo
componentes simétricas directamente sobre la (ver apartado siguiente) indica que:
figura sin necesidad de relacionar los vectores
uuuu
r
(figura 9). uur Ea
Vd =
En efecto, sean los puntos D y E tales que 3
BDCE sea un rombo compuesto de dos uuuur
u
uu DA
r
triángulos equiláteros BDC y BCE y siendo O' el Vi =
3
uur uuuuu r
Vo = OO '
E
V2
+ Vd
V3 B
O V2 V3 C
O O'
Vo
D V1
Vi
V1
Sistema dado
A
Fig. 9: Sistema homopolar.
2.6 Cálculo de las componentes simétricas
uuu
r uuu uuu
r r
Sean los puntos D y E tales que (BDCE) sea un DA = a.BC + BA
rombo compuesto de dos triángulos equiláteros uuur uuur uuur uuur
u u
(BDC) y (BCE). = a.BO + a.OC + BO + OA
uuur uuur
u uuur
u
uuu uuu uuu
r r r
n Sistema directo: EA = EB + BA, pero como = OA + OB ( −a − 1) + a.OC
uuur
u uuur uuur
u
uuu
r uuu
r = OA + a.2 OB + a.OC
EB = a2 .BC , se tiene que: uu
r uur uur uur
= V1 + a2.V2 + a.V3 = 3Vi
uuu
r uuu uuu
r r
EA = a2 .BC + BA
uuur uuur uuur uuur
u u uuuur
u
= a2 .BO + a2 .OC + BO + OA uu DA
r
uuur uuur
u uuuu
r Vi =
( )
= OA + OB −a2 − 1 + a2 .OC 3
uuur
u uuur uuur
u
= OA + a.OB + a2 .OC n Sistema homopolar: sea O' el baricentro del
uuuuu uuuur uuuuu
r u r
uu
r uur uur uur triángulo ABC. Se tiene: O ' A + O 'B + O ' C = 0
= V1 + a.V2 + a2 .V3 = 3Vd
uu uur uur
r uur
V1 + V2 + V3 = 3Vo
uuuur uuur uuur uuur
u u
uuu EA
r = OA + OB + OC
Vd = uuuuu uuuuu uuuuu uuuur uuuuu uuuuu
r r r u r r
3 = OO ' + O ' A + OO ' + O 'B + OO ' + O ' C
uuuuu uuuuu uuuur uuuuu
r r u r uuuuu
r
uuu uuu uuu
r r r = 3 OO ' + O ' A + O 'B + O ' C = 3 OO '
n Sistema inverso: DA = DB + BA , pero como
uuu
r uuu
r uur uuuuu
r
DB = a.BC , se tiene que: Vo = OO '
Cuaderno Técnico Schneider n° 018 / p. 10

11. 2.7 Conclusión: aplicación a la electrotecnia
El método expuesto en el párrafo anterior tiene pueden medirse tanto las impedancias
un interés inmediato en la electricidad en caso simétricas de los materiales eléctricos (ver
de redes trifásicas lineales y a frecuencia única. capítulo 3) como las componentes simétricas de
En efecto, los sistemas trifásicos aplicados a las un sistema de tensiones o de corrientes
redes eléctricas pueden estar desequilibrados (capítulo 4, ejemplo nº 4).
por asimetría de la carga o por defectos. Es Notas
evidente la simplicidad que ofrecen estos n por simplificación, en el texto que sigue, los
cálculos, basados en la superposición de tres vectores tensión y corriente se escribirán sin la
sistemas independientes, al permitir tratarlos flecha,
separadamente, convirtiendo cada uno en un
caso simple monofásico. n las componentes simétricas de tensiones y
corrientes elegidas para la representación
Observaremos que estas manipulaciones simple del sistema, son las de la fase 1:
matemáticas corresponden, de hecho, a una
realidad física de los fenómenos, puesto que V1 =Vd + Vi + Vo.
Cuaderno Técnico Schneider n° 018 / p. 11

12. 3 Aplicaciones elementales
3.1 Método de cálculo de los regímenes desequilibrados
Principio de superposición
Vamos a examinar el comportamiento de una
Zd
red trifásica lineal y simétrica, es decir, E
compuesta de impedancias constantes e d
idénticas para las tres fases (que es el caso Vd
práctico) que no produce más que fuerzas
Zi
electromotrices (f.e.m.) equilibradas pero cuyas
corrientes y tensiones pueden estar i
desequilibradas debido a la conexión a una zona Vi
asimétrica D. Zo
Las f.e.m. constituyen por naturaleza los
o
sistemas directos, si los sistemas inverso y Vo
homopolar son nulos.
Se interpreta el funcionamiento de la red como
la superposición de tres regímenes que Fig. 10.
corresponden, cada uno, a uno de los sistemas
directo, inverso y homopolar.
En efecto, en esta red lineal y simétrica, las Método de resolución práctica
corrientes de cada sistema se relacionan sólo
con las tensiones del mismo sistema y El método resumido a continuación se
recíprocamente por medio de las impedancias desarrollará con detalle en el ejemplo del párrafo
del sistema considerado. Téngase presente que siguiente (defecto monofásico a tierra):
estas impedancias Zd, Zi y Zo son función de las n la red se divide en 2 zonas:
impedancias reales y también de las
o una zona asimétrica D (red desequilibrada),
inductancias mutuas.
o una zona simétrica S (red equilibrada),
Para una red que presente una sola f.e.m. y con
las componentes simétricas de tensión y de n se escriben las ecuaciones que relacionan las
corriente situadas respectivamente en el lado D corriente y tensiones:
de la asimetría Vd, Vi, Vo, Id, Ii, Io, las relaciones o en la zona D (componentes reales),
que definen a los tres regímenes son:
o en la zona S (componentes simétricas),
E = V d + Zd . I d
o continuidad en la frontera D-S,
0 = Vi + Z i . I i
o funcionamiento en la zona S,
0 = Vo + Zo . Io,
n la resolución matemática de las ecuaciones
representadas esquemáticamente en la permite calcular los valores de las componentes
figura 10. simétricas y de las componentes reales de las
Para las redes con varias fuentes (generadores) corrientes y tensiones de las zonas D y S.
estas ecuaciones son válidas con la condición Hay que indicar que los esquemas
de considerar E y Zd, Zi, Zo, respectivamente representativos de los sistemas simétricos
como la f.e.m. y como las impedancias internas ofrecen la posibilidad de calcular directamente
del generador equivalente de Thévenin. los valores de las componentes simétricas.
Cuaderno Técnico Schneider n° 018 / p. 12

13. 3.2 Defecto fase-tierra (llamado defecto homopolar)
Se supone que el circuito está sin carga.
Planteamiento de las ecuaciones E fase 1
n Aislamiento de la zona de asimetría a2E fase 2
(figura 11)
n Ecuaciones de las componentes reales aE fase 3
en (D)
d, i, o
 I 2 = I3 = 0 Vd ,Vi , Vo
 zona S
 V1 = Z I1
3 2 1
Estas ecuaciones describen el caso examinado V3 V2 V1
y son las únicas que corresponden a la figura. Z
zona D
n Ecuaciones de las componentes simétricas
en (S).
Fig. 11.
I1 = I d + Ii + Io

I 2 = a . I d + a. Ii + Io
2
Estas tres ecuaciones se encuentran

I3 = a. I d + a . Ii + Io
2 sistemáticamente en todos los casos de cálculo
 de regímenes desequilibrados con una sola
 V1 = Vd + Vi + Vo fuente de tensión.

 V2 = a .Vd + a.Vi + Vo
2
Resolución de las ecuaciones
 V = a.V + a2. V + V
 3 d i o
n Los valores de las componentes simétricas
de las corrientes y de las tensiones:
Estas ecuaciones relacionan respectivamente
E + 0 + 0 = Vd + Vi + Vo + Zd.Id + Zi.Id + Zo.Io
las corrientes reales y las tensiones reales con
= 3 Z.Io + ( Zd + Zi + Zo). Io
sus componentes simétricas. Se encontrarán de
forma idéntica en todos los cálculos de siendo:
regímenes desequilibrados. Se deducen de las
E
definiciones anteriores (capitulo 2). Io = Id = Ii =
Zd + Zi + Zo + 3Z
n Continuidad en la frontera D-S
Por combinación entre las ecuaciones de las E
componentes reales en (D) y las ecuaciones de Vd = E − Zd . Id = E − Zd
Zd + Zi + Zo + 3Z
las componentes simétricas en (S), se obtiene:
a2.I d + a. Ii + Io = 0 Zi + Zo + 3Z
 Vd = E
 Zd + Zi + Zo + 3Z
a.Id + a . Ii + Io = 0
2
 V + V + V = Z. I
 d

i o 1
V i = – Z i .I i
E
 I1 Vi = − Zi
I = Ii = Io = Zd + Zi + Zo + 3Z
⇒ d 3
 V + V + V = 3 Z. I
 d i o o V o = – Z o .I o
n Ecuaciones del funcionamiento de S E
Vo = − Zo
Zd + Zi + Zo + 3Z
E = Vd + Zd . Id

0 = Vi + Zi + Ii
0 = V + Z . I
 o o o
Cuaderno Técnico Schneider n° 018 / p. 13

14. n Esquema de la red, según las componentes  
Z + a. Zi + a2 . Zo
simétricas (figura 12). V3 = a.E  1 − d 
 Zd + Zi + Zo + 3Z 
 
n Valores de las tensiones y de las corrientes
reales:
Nota:
I 1 = Id + I i + Io
 Zd + a.Zi + a 2 .Zo 
3E El término  1 − Z + Z + Z + 3Z
  se llama factor

I1 =  d i o 
Zd + Zi + Zo + 3Z
de «defecto a tierra». Su valor varía entre 1 y
I2 = 0 1,8.
Casos particulares
I3 = 0
n Con defecto franco, Z = 0, la corriente de
defecto fase-tierra toma el valor:
V1 = Z.I1
3E
I1 =
V1 = 3Z
E Z d + Zi + Z o
Zd + Zi + Zo + 3Z
n Con defecto impedante a tierra,
3Z >> Zd + Zi + Zo, la corriente de defecto de
fase-tierra se define por la impedancia de
V2 = a2 . Vd + a. Vi + Vo =
defecto:
Zi + Zo + 3Z
= a2.E − E
Zd + Zi + Zo + 3Z I1 = .
Z
Zi
− a.E −
Zd + Zi + Zo + 3Z
Zo Vd
−E =
Zd + Zi + Zo + 3Z d
( ) ( )
E
Zi a − a + Zo a − 1 + 3a . Z
2 2 2
Vi
Zd
=E
Zd + Zi + Zo + 3Z i
Zi
Vo
 Z + a2.Zi + a. Zo  o
V2 = a2 .E  1 − d 
 Zd + Zi + Zo + 3Z  Zo
 
d = i= o
3Z
V3 = a. Vd + a2 . Vi + Vo =
Fig. 12.
Zi + Zo + 3Z
= a.E −
Zd + Zi + Zo + 3Z
Zi
− a2 .E −
Zd + Zi + Zo + 3Z
Zo
−E =
Zd + Zi + Zo + 3Z
=E
( )
Zi a − a 2 + Zo (a − 1) + 3a. Z
Zd + Zi + Zo + 3Z
Cuaderno Técnico Schneider n° 018 / p. 14

15. 3.3 Defecto bifásico a tierra
(figura 13)
−E Zi
Io = x =
Escritura de las ecuaciones Zi ( Zo + 3Z ) Zi + Zo + 3Z
Zd +
n En la zona (D) Zi + Zo + 3Z
− E Zi
I1 = 0
 =
 Z d .Zi + ( Z d + Zi ) (3Z + Zo )
 V2 = V3 = Z ( I2 + I3 )

n En la zona (S) E Zi ( Zo + 3Z )
Vd = Vi = x
Zi ( Z o + 3Z ) Zi + Zo + 3Z
Zd +
I1 = I d + Ii + Io Zi + Zo + 3Z

I 2 = a . I d + a. Ii + Io
2
 E Zo .Zi
I3 = a. I d + a . Ii + Io
2
Vo = x
 Zi ( Zo + 3Z ) Zi + Zo + 3Z
 V1 = Vd + Vi + Vo Zd +
 Zi + Zo + 3Z
 V2 = a .Vd + Vi + Vo
2
 V = a.V + a2. V + V I1 = 0
 3 d i o
Zo + 3Z − a.Zi
n Continuidad en la frontera (D) - (S) I2 = − j 3 E
Zd .Zi + ( Zd + Zi )( Zo + 3Z )
 I d + Ii + I o = 0

 Vd = Vi Zo + 3Z − a2 .Zi
 V = V + 3 Z. I I3 = j 3 E
 o d o
Zd .Zi + ( Zd + Zi )( Zo + 3Z )
n Funcionamiento de (S) 3Zi ( Zo + 2Z )
V1 = E
Zd .Zi + ( Zd + Zi )( Zo + 3Z )
E = Vd + Zd . I d

0 = Vi + Zi . Ii − 3Z. Zi
0 = V + Z + I V2 = V3 = E
 o o o Zd .Zi + ( Zd + Zi ) ( Zo + 3Z )
Resolución de las ecuaciones
E fase 1
E
Id = = a2E fase 2
Zi ( Zo + 3Z )
Zd +
Zi + Zo + 3Z
aE fase 3
Zi + Zo + 3Z
=E
Zd .Zi + (3Z + Zo )( Zd + Zi ) d, i, o,
Vd ,Vi , Vo
zona S
3 2 1
−E Zo + 3Z
Ii = x =
Zi ( Zo + 3Z )
V3 V2 V1
Zi + Zo + 3Z
Zd + Z zona D
Zi + Zo + 3Z
−E ( Zo + 3Z )
=
Zd .Zi + ( Zd + Zi ) (3Z + Zo ) Fig. 13.
Cuaderno Técnico Schneider n° 018 / p. 15

16. n Esquema de la red según las componentes
Vd
simétricas (figura 14) .
d
Casos particulares E
Zd
n Defecto franco, con Z = 0: la corriente del
defecto fase-tierra tomará el valor: Vi
3E.Zi i
I 2 + I3 = −
Zd .Zi + Zi .Zo + Zd .Zo Zi
3Z
n Defecto bifásico aislado, con Z = ∞, la o
corriente de defecto de fase vale entonces:
Zo
I 2 = − I3 =E
(a 2
−a ) = − jE 3
Vo
Fig. 14.
Z d + Zi Z d + Zi
3.4 Defecto trifásico
(Figura 15).
E fase 1
Escritura de las ecuaciones
a2E fase 2
n En la zona (D)
V 1 = V 2 = V 3 = Z ( I1 + I2 + I3 ) fase 3
aE
n En la zona (S)
Vd ,Vi ,Vo
I1 = I d + Ii + Io zona S

I 2 = a . I d + a.Ii + Io
2
d i o

I3 = a.I d + a . Ii + Io
2
V3 V2 V1

 V1 = Vd + Vi + Vo Z zona D

 V2 = a .Vd + a.Vi + Vo
2
 V = a.V + a2 .V + V
 3 d i o Fig. 15.
Vd = 0
n Continuidad en la frontera (D) - (S)
 Vo
I1 + I 2 + I3 = 3 Io = Z
 d
 Vd = Vi = 0 E
V = V = V = V Zd
 1 2 3 o


Zi
n Funcionamiento de (S)
E = Vd + Zd . Id Zo

0 = Vi + Zi . Ii
0 = V + Z . I Fig. 16.
 o o o
Cuaderno Técnico Schneider n° 018 / p. 16

17. Resolución de las ecuaciones E
I3 = a
Zd
E
Id = y Ii = I o = 0
Zd
V1 = V2 = V3 = 0
Vd = Vi = Vo = 0 Los resultados son independientes de los
valores de Z, Zi y Zo.
E
I1 = n Esquema de la red según las componentes
Zd
simétricas (figura 16).
E
I 2 = a2
Zd
3.5 Red con cargas desequilibradas
(Figura 17). n Continuidad en la frontera (D) - (S)
Escritura de las ecuaciones I o = 0

n En la zona (D)  I d = Ii
V − V = Z . I
I1 = 0  d i c d
V3 − V2 = I3 . Zc = − I2 . Zc n Funcionamiento de (S)
n En la zona (S) E = Vd + Zd . Id

0 = Vi + Zi . Ii
I1 = I d + Ii + Io 0 = V + Z . I
 o o o

I 2 = a . I d + a. Ii + Io
2
 Resolución de las ecuaciones
I3 = a. I d + a . Ii + Io
2

 V1 = Vd + Vi + Vo Id =
E
 Z d + Zi + Zc
 V2 = a . Vd + a. Vi + Vo
2
 V = a. V + a2. V + V
 3 d i o
E
Ii = −
Zd + Zi + Zc
Io = 0
E fase 1
E ( Zi + Z c )
a2E fase 2 Vd =
Z d + Zi + Z c
aE fase 3
d , i, o, E.Zi
Vd ,Vi ,Vo Vi =
zona S Z d + Zi + Zc
2 1
3
Vo = 0
V3 Zc V2 V1
zona D I1 = 0
E 3
I2 = − j
Fig. 17. Zd + Zi + Zc
Cuaderno Técnico Schneider n° 018 / p. 17

18. jE 3
I3 =
Z d + Zi + Zc
Vd
E ( 2 Zi + Zc )
V1 = d
Z d + Zi + Z c E
Zd
V2 =
(
E a2.Zc + Zi ) Vi
Zc
Z d + Zi + Zc
i
E (a.Zc − Zi ) Zi
V3 =
Z d + Zi + Zc
n Esquema de la red según las componentes Zo
simétricas (figura 18).
Casos particulares Fig. 18.
n Carga de baja potencia, siendo Zc → ∞ :
n Cortocircuito bifásico aislado, con Zc = 0.
I1 e I3 → 0 y V1, V2 y V3 La corriente de defecto es, en este caso:
tienden hacia los valores de red simétrica, es E 3
decir, hacia E, a2E, a.E.
I3 = − I 2 = j
Z d + Zi
3.6 Impedancias asociadas a las componentes simétricas
En este párrafo, se pasa revista a los elementos n La reactancia inversa es inferior a la
principales que pueden intervenir en una red reactancia directa transitoria.
eléctrica. n La reactancia homopolar no se toma en
Para las máquinas rotativas y los consideración salvo que el neutro del alternador
transformadores, los órdenes de magnitud de esté conectado a la tierra directamente o a
las impedancias son idénticos en porcentaje: través de una bobina o de una resistencia.
  Su valor es del orden de la mitad de la
S
 z% = 100 Z n
 2

 reactancia subtransitoria.
 Un 
Máquinas sincrónicas
Las generatrices provocan el nacimiento de la
componente directa de la potencia. Los defectos
Reactancia polos entrehierro
son los creadores de las componentes inversa y
% salientes constante
homopolar que se dirigen desde el punto de
defecto hacia los elementos equilibrados, subtransitoria 30 20
atenuándose progresivamente. transitoria 40 25
n Después de una perturbación, la reactancia síncrona 120 200
directa de una máquina pasa del valor
subtransitorio al valor síncrono. En el cálculo del
defecto, se pueden tomar los valores en % Fig. 19.
(figura 19).
Cuaderno Técnico Schneider n° 018 / p. 18

19. Máquinas asíncronas o líneas con 2 conductores por fase (400 kV)
La componente directa genera, en los motores, Rd = Ri ≈ 0,04 Ω /km
los campos rotativos en el sentido directo Xd = Xi ≈ 0,32 Ω /km
(par útil).
Cd = Ci ≈ 12 nF/km
La componente inversa produce los campos
n La impedancia homopolar vale aproximada-
rotativos generadores de pares de frenado.
mente tres veces la impedancia directa.
n Usualmente podemos considerar la
La capacidad homopolar se puede valorar en
reactancia directa como una impedancia pasiva
unas seis veces la capacidad directa.
U2 / (P-jQ).
n La reactancia inversa varía entre el 15 y el Cables
30%. Es aproximadamente igual a la reactancia n La reactancia y la capacidad directas e
de arranque. inversas dependen de la geometría de los
n La reactancia homopolar es muy baja. cables.
Transformadores Rd = Ri
Xd = Xi ≈ 0,1 a 0,15 Ω /km
La circulación de una corriente homopolar por
los arrollamientos de un transformador precisa Cd = Ci ≈ 120 a 320 nF/km
una conexión con un punto neutro unido a tierra n Las características homopolares de un cable
o a un conductor de neutro. no se deducen fácilmente de las características
n Los transformadores presentan, a las directa e inversa. En general son despreciables
corrientes de los sistemas directo e inverso, una ante las de los transformadores que alimentan
impedancia igual a su impedancia de dichos cables.
cortocircuito, del orden del 4 al 15%.
n La reactancia homopolar depende de la
conexión de los arrollamientos y de la naturaleza
del circuito magnético. La tabla de la figura 20
resume los diferentes casos detallados en las
figuras 22 a y b.
Transformador Reactancia
Lineas aéreas (visto lado secundario) homopolar
Consideremos las líneas transpuestas. Sin neutro ∞
n La impedancia y la capacidad directas e Yyn o Zyn flujo libre ∞
inversas dependen de la geometría de la línea. flujo forzado 10 a 15 Xd
o líneas con 1 conductor por fase (63, 90, 150 y Dyn o YNyn Xd
225 kV)
primario zn 0,1 a 0,2 Xd
Rd = Ri ≈ 0,16 Ω /km
Xd = Xi ≈ 0,4 Ω /km
Fig. 20.
Cd = Ci ≈ 9 nF/km
Cuaderno Técnico Schneider n° 018 / p. 19

20. 3.7 Formulario de recapitulación
Parámetros empleados:
n Tensión eficaz compuesta de la red trifásica U
U
n tensión eficaz simple de la red trifásica V=
3
n corriente de cortocircuito, en módulo Icc
n corriente de defecto a tierra, en módulo Itierra
n impedancias simétricas Zd, Zi, Zo
n impedancia de cortocircuito Zc
n impedancia de tierra Z
La tabla de la figura 21 resume los valores de las corrientes, en módulos, en los diferentes casos de
asimetría.
Tipo de asimetría Asimetría impedante Asimetría franca
(Z = 0 y/o Zc = 0)
U 3 U 3
Cortocircuito monofásico Icc = Icc =
Zd + Zi + Zo + 3Z Z d + Zi + Z o
U 3 Zi U 3 Zi
Itierra = Itierra =
Cortocircuito bifásico a tierra Zd .Zi + ( Zd + Zi ) ( Zo + 3Z ) Zd .Zi + Zi .Zo + Zd .Zo
(Zc = 0)
U U
Cortocircuito bifásico aislado Icc = Icc =
Z d + Zi + Z c Z d + Zi
(Z = ∞)
U U
Cortocircuito trifásico Icc = Icc =
Z d + Zc 3 Zd 3
(Z cualquiera)
Fig. 21.
Cuaderno Técnico Schneider n° 018 / p. 20

21. Conexión Valor de la reactancia homopolar
Esquema unifilar del transformador, vista desde:
primario secundario terciario equivalente los bornes bornes bornes
primarios 1 secundarios 2 terciarios 3
1 2 infinito infinito
1 2
1 2 infinito infinito
1 2
Flujos libres
Flujos libres
infinito
1 X11 2 infinito
Flujos forzados
Flujos forzados
1 2 X11 = 10 a 15
1 2 infinito
veces Xcc
1 2 X12 = Xcc X12 = Xcc
1
infinito infinito
1 2
1 2
X12
X12 = Xcc infinito
1 2
1 2
1 2 infinito infinito
1 2
X 22
1 2 infinito X22 = 1% de Sn
2
1
Flujos libres
infinito Flujos libres
1 X11 2 infinito
Flujos forzados
1 2 X11 = 10 a 15 Flujos forzados
1 2 veces Xcc infinito
Fig. 22 (a).
Cuaderno Técnico Schneider n° 018 / p. 21

22. Conexión Valor de la reactancia homopolar
Esquema unifilar del transformador, vista desde:
primario secundario terciario equivalente los bornes los bornes los bornes
primarios 1 secundarios 2 terciarios 3
X 22
1 2 infinito X22 = 1% de Xn
1 2
Flujos libres Flujos libres
X22
infinito X22 = 1% en X n
1 2 Flujos forzados Flujos forzados
X22
X11 = 10 a 15 X = 1% de X
1 2 22 n
1 2 veces Xcc
1 2 infinito infinito
1 2
Flujos libres
X11 infinito
2
Flujos forzados
1 infinito infinito
X11 = 10 a 15
1 2 3 3
veces X12
2
X2 X02
( x2 + x02 )( x3 + x03 ) ( x1 + x01 )( x2 + x02 )
X01 X1 x1 + x3 +
x 2 + x 3 + x 02 + x 03 x1 + x 2 + x01 + x02
1
2
1 3 X3 X03 ( x1 + x01)( x3 + x03 )
3 x2 +
x1 + x 3 + x 01 + x 03
2
X2
X1
x 2 x3
1 x1 + infinito infinito
X3 x 2 + x3
1 2 3
3
2
x 2 ( x 3 + x 03 ) x 2 ( x1 + x 01 )
X2
X1
X01 x1 + x3 +
1 x 2 + x 3 + x 03 infinito x1 + x 2 + x 01
X3
1 2 3 X03
3
2
X2
X1
1 X33 X1 + X2 = X12 infinito X 33 = 1% de Xn
1 2 3
3
Fig. 22 (b).
Cuaderno Técnico Schneider n° 018 / p. 22

23. 4 Ejemplos resueltos
4.1 Ejemplo 1: Poder de corte de un interruptor automático
Esquema de la figura 23
Problema 100MVA
¿Qué poder de ruptura ha de tener, como
mínimo, el interruptor automático? 2500 MVA
17 kV
Solución
8% 36 kV
Cuando interviene el interruptor automático, la
X'd = 35%
componente aperiódica está latente en el interior X'i = 25%
de la red pero no en los devanados del
alternador.
Fig. 23.
n Impedancias:
o del alternador, referidas al secundario del
transformador: o monofásico
2
35 36 36 3
Za directa: x = j0,18 Ω = = 18 kA
100 2500 1,22 + 1,17 + 1,0
25 362 o bifásico aislado
Za inversa: x = j0,13 Ω
100 2500 U 36
Icc = = = 15 kA
Zd + Zi 1,22 + 1,17
Za homopolar: despreciable.
o del transformador, referida al secundario del o bifásico a tierra
transformador:
U Z o − a Zi
8 362 Icc =
Zt directa: x = j1,04 Ω Zd Zi + Zi Zo + Zo Zd
100 100
36 . 1,915
= = 17,6 kA
Zt inversa: j1,04 Ω 3,91
Zt homopolar = j1,04 Ω
n el interruptor automático deberá cortar una
o totales
corriente de cortocircuito de 18 kA o, lo que es
Z directa = j1,22 Ω lo mismo, su potencia de ruptura deberá ser de:
Z inversa = j1,17 Ω 18 x 36 3 = 1122 MVA .
Zt homopolar = j1,04 Ω
n corrientes de cortocircuito:
o trifásico
U/ 3 36 / 3
Icc = = = 17 kA
Zd 1,22
Cuaderno Técnico Schneider n° 018 / p. 23

24. 4.2 Ejemplo 2: Poder de corte de un interruptor automático
Esquema de la figura 24. Solución
Problema n Esquema global directo o inverso (reducción
a 60 kV) (figura 25)
En una red de 60 kV, determinar el poder de
ruptura de los interruptores automáticos de los U2 25 60 2 25
centros C y E, que alimentan a la línea de 15 km. a=j x = x = j 22,5 Ω
Pcc 100 40 100
La reactancia de cortocircuito de los
transformadores de grupo y de red es del 10% y
U2 10 602
la de los otros transformadores, del 8%. b = jUcc = x = j9 Ω
Pcc 100 400
Para una línea de 60 kV la reactancia es de
0,4 Ω/km en régimen directo e inverso y de
C1 = j0,40 x 60 = j24 Ω
3 x 0,40 Ω/km en régimen homopolar.
C2 = j0,40 x 50 = j20 Ω
Los grupos presentan una reactancia directa o
inversa de 25%. C3 = j0,40 x 40 = j16 Ω
Las cargas de potencia activa P presentan C4 = j0,40 x 40 = j16 Ω
una reactancia equivalente estimada
de j.0,6 U 2 /P.
40 MVA
40 MVA
30 MW
A
40 km 60 km
15 MVA 40 MVA
8 MW 12 MVA 15 km 20 MVA 14 MW
10 MW
B C
E
10 MW
15 MVA
50 MVA
40 km 50 km
red
150 kV
D
1500 MVA
20 MVA
20 MVA
Fig. 24.
Cuaderno Técnico Schneider n° 018 / p. 24

25. U2 8 602 U2 25 602 25
d = jUcc = x = j19,2 Ω k=j x = x = j 45 Ω
Pcc 100 15 Pcc 100 20 100
U2 602 U2 8 60 2
e=j x 0,6 = x 0,6 = j216 Ω I = jUcc = x = j7,2 Ω
P 10 Pcc 100 40
U2 8 602 U2 602
f = jUcc = x = j24 Ω m=j x 0,6 = x 0,6 = j72 Ω
Pcc 100 12 P 30
U2 602 U2 602
g= j x 0,6 = x 0,6 = j270 Ω n = jUcc x =
10
x = j7,2 Ω
P 8 Pcc 100 50
U2 8 602
h = jUcc = x x19,2 = Ω U2 602
Pcc 100 15 o=j = = j 2,4 Ω
Pcc 1500
U2 602 p = j0, 4 x15 = j 6 Ω
i= j x 0,6 = x 0,6 = j216 Ω
P 10
U2 8 602
2 2 q = jUcc = x = j14,4 Ω
U 10 60 Pcc 100 20
j = jUcc = = j18 Ω
Pcc 100 20
U2 602
r=j x0,6 = x0,6 = j154 Ω
P 14
a
b
A
d
m
c4 c1
e
g l
f E
B C
p q r
n
i
c3 c2
o
h
D
j
k
Fig. 25.
Cuaderno Técnico Schneider n° 018 / p. 25

26. n Esquema global homopolar (reducción a
60 kV) (figura 26).
esquema directo/inverso
Los transformadores del centro de
C j6 E j168,4
transformación detienen las corrientes
homopolares en sus arrollamientos en triángulo.
b’ = b = j9 Ω j6,45
c’1 = 3c1 = j72 Ω
c’2 = 3c2 = j60 Ω
c’3 = 3c3 = j48 Ω
esquema homopolar
c’4 = 3c4 = j48 Ω
C j18 E
d’ = ∞
f’ = ∞ j6,09
h’ = ∞
j’ = j = j18 Ω
l’ = ∞
Fig. 27.
n’ = n = j7,2 Ω
p’ = 3p = j18 Ω
esquema directo
q’ = ∞ j6 j168,4
C E
n Esquemas reducidos
Para el estudio que nos interesa se pueden
reducir los esquemas a lo indicado en C y E
(figura 27).
n Dimensionamiento del interruptor automático
de línea, lado C:
esquema homopolar
Caso 1: defecto lado barras (figura 28)
C j18 E
Zd = j6 + j168,4 = j174,4 Ω ¥
Zo = ∞
Fig. 28.
b'
A
d'
c'4 c'1
l'
f' E
B C
p' q'
n'
c'3 c'2
h'
D
j'
Fig. 26.
Cuaderno Técnico Schneider n° 018 / p. 26

27. o Icc trifásica es igual a:
U 60
= = 0,195kA esquema directo
Zd 3 174,4 3 C
línea abierta
con lo que:
j6,45
Pcc = U I 3 = 20,7MVA
o Icc monofásica es igual a:
U 3
=0 esquema homopolar
Z d + Zi + Z o
C
línea abierta
con lo que Pcc = 0.
j6,09
Caso 2: Defecto lado línea (figura 29)
Zd = j6,45 Ω
Zo = j6,09 Ω
Fig. 29.
o Icc trifásica es igual a:
U 60
= = 5,37kA
Zd 3 6,45 3
esquema directo
con lo que: C j6 E
Pcc = UI 3 = 558,1 MVA
j6,45
o Icc monofásica es igual a:
U 3 60 3
= = 5,47 kA
Zd + Zi + Z o 18,99
esquema homopolar
con lo que: C j18 E
Pcc = UI 3 = 568,7MVA
j6,09
El interruptor automático de línea en el punto C
deberá estar dimensionado para 570 MVA.
n dimensiones del interruptor automático de
Fig. 30.
línea, lado E:
Caso 1: Defecto lado barras (figura 30)
Zd = j6 + j6,45 = j12,45 Ω
esquema directo
Zo = j18 + j6,09 = 24.09 Ω j168,4
E
o Icc trifásica es igual a
U 60
= = 2,782 kA
Zd 3 12, 45 3
con lo que Pcc = UI 3 289,2MVA
esquema homopolar
o Icc monofásica es igual a:
E
U 3 60 3
= = 2,121 kA
Zd + Zi + Zo 48,99
Fig. 31.
con lo que Pcc = UI 3 = 220,5MVA
Cuaderno Técnico Schneider n° 018 / p. 27

28. Caso 2: Defecto lado línea (figura 31) o Icc monofásica es igual a:
Zd = j168,4 Ω U 3
=0
Zo = ∞ Z d + Zi + Z o
o Icc trifásica es igual a:
con lo que: Pcc = 0
U 60
= = 0,206 kA El interruptor automático de línea, en el punto E,
Zd / 3 168, 4 3
deberá estar dimensionado para 290 MVA.
con lo que: Pcc = UI 3 = 21,4MVA
4.3 Ejemplo 3: Regulación de protecciones homopolares en una
red MT con neutro a tierra
Esquema de la figura 32.
Problema
n
¿Cual deberá ser la regulación de intensidad de
los relés homopolares de las diferentes Con
derivaciones?
Solución i
HT / MT
Se parte de las fórmulas del párrafo de defecto
fase-tierra; se aprecia que la impedancia de
tierra Rn es equivalente a tres impedancias de
valor 3 Rn situadas cada una sobre una fase de
Rn
la red puesta a tierra directamente. La corriente
homopolar en el punto del defecto a tierra se 2
divide en dos caminos paralelos:
C02
n el primero corresponde a la impedancia de
neutro 3.Rn, en serie con la impedancia
1
homopolar del transformador y del trozo de
cable comprendido entre el defecto y el
transformador. O sea: 3.Rn + ZOT + ZOL, C01 I1
Zdefecto
n el segundo corresponde a la puesta en
paralelo de los circuitos capacitivos del
conductor
−j
n
∑ Coi ω Fig. 32.
1
Si se opera con el máximo rigor, se deben tener 3E
I1 = a través de
en cuenta las impedancias del transformador y Zd + Zi + Zo + 3Z
de las líneas, que prácticamente son
despreciables ante las impedancias capacitivas. Ro = (3Rn + ZOT + ZOL) en paralelo con
j
La corriente de defecto a tierra I1 (ver defecto −
fase-tierra) ∑ (Coi ) ω , o sea:
Cuaderno Técnico Schneider n° 018 / p. 28

29. 3Rn + ZOT + ZOL
Zo =
 n  V3 E3
1 + j (3Rn + ZOT + ZOL )  ∑ Coi  ω (5500 V) (3175 V)
 1 
 
Vo 120o
y por sustitución, se tiene la expresión de la 120o Vd
(3175 V)
figura 33.
120o E1
Si, como es habitual, Zd, Zi, ZOT, ZOL son 120o (3175 V)
prácticamente despreciables respecto al valor
de 3 Rn y el defecto es franco (Z = 0), entonces
se tiene:
V2 E2
(5500 V) (3175 V)
E  n 
I1 ≈ + j3  ∑ Coi  ωE
Rn  1 
  Fig. 34.
La contribución de cada derivación sana a la
corriente de tierra es, pues, de 3Coi ω E (en
módulo). Aplicación numérica y representación gráfica
Para evitar disparos intempestivos, la regulación (figura 34)
del relé homopolar de cada una de las Se supone que se produce un defecto franco en
derivaciones ha de ser superior a la corriente una red de 5 500 V, 50 Hz, con neutro
capacitiva mencionada. impedante, con:
Esta corriente depende de la naturaleza y de la Rn = 100 Ω,
longitud de los conductores.
Co = 1 µF,
Por ejemplo:
Z = Zd = Zi = ZOT = ZOL = 0,
o para una línea de 15 kV, la capacidad
homopolar es de alrededor de 5 nF/km, lo que E = 5500 / 3 = 3175 V
representará una corriente de:
Zo = 3 Rn /(1 + j3Rn.Co.ω),
3 x 5.10−9 x 314 x15000 / 3 = 0,04 A / km
I1 = (3 175/ 100) + j3 x 3175 x 10-6 x 314 ≈
o sea, una corriente de 4 A para 100 km, ≈ (32 + j3) A,
o para un cable tripolar de 15 kV, la capacidad I2 = I3 = 0,
homopolar es de unos 200 nF/km, lo que V1 = 0,
provoca la circulación de una corriente de:
 3 
3 x 200.10−9 x 314 x15000 / 3 = 1,63 A / km V2 = ja.E 3 = −3175  1,5 + j
  voltios,

 2 
o sea, de unos 2 A/km,
 3 
o estos valores de corriente capacitiva deben V3 = E (a − 1) = 3175  −1,5 + j
  voltios.
compararse con los de la corriente que atraviesa  2 
la impedancia de neutro y que alcanza varias
decenas e incluso centenas de amperios.
  n  
3E 1 + j (3Rn + ZOT + ZOL )  ∑ Co i  ω
  1  
   
I1 =
  n  
( Zd + Zi + 3Z ) 1 + j (3Rn + ZOT + ZOL )  ∑ Coi  ω + 3 (Rn + ZOL + ZOT
 1  
   

Fig. 33.
Cuaderno Técnico Schneider n° 018 / p. 29

30. 4.4 Ejemplo 4: Medición de las componentes simétricas de
un sistema de tensión y de corriente
Sistema de tensión El transformador auxiliar T1 genera una
corriente proporcional a (I1 - I3) que circula a
n La componente homopolar se mide con la través de Z, igual a: – a2.R.
ayuda de tres transformadores de tensión (TT)
cuyos primarios están conectados entre fase y La tensión en los bornes del voltímetro es
neutro y los secundarios en serie para alimentar proporcional a:
( I3 − I2 ) + ( I1 − I3 ) ( − a2 )
un voltímetro (figura 35)
V = 3 Vo . k
siendo k la relación de transformación. = I3 − I2 − a2. I1 + a2. I3
n La componente directa se mide con la ayuda ( )
= − a2 I1 + a. I2 + a2 . I3 = −3 a2 . Id
de 2 TT montados entre V1 y V2 por una parte y
V2 y V3 por otra (figura 36). El primer TT está
V1
cargado con una resistencia pura R. El segundo,
con una inductancia y una resistencia de valor V2
tal que: V3
jπ / 3
Z = − a.R = R.e
Z está formada por la serie de una resistencia
transformación V3 V2 V1
(R/2) y una reactancia ( R 3 / 2 ).
de tensión
Los dos circuitos están en paralelo sobre un relación k
amperímetro que medirá una corriente
proporcional a:
( V1 − V2 ) +  − a2 ( V2 − V3 )
  kV3 kV2 kV1
( )
= V1 − V2 1 + a2 + a2.V3
kV1 + kV2 + kV3 =V = 3 Vo .k
V
= V1 + a.V2 + a2.V3 = 3 Vd
Fig. 35.
n La componente inversa se mide de la misma V1
manera que la directa, pero con la inversión de V2
polaridad entre los bornes 2 y 3.
V3
( V1 − V3 ) +  − a2 ( V3 − V2 )
 
(
= V1 − a2.V2 − V3 1 + a2 )
= V1 + a2 .V2 + a.V3 = 3 Vi
Sistema de corriente
Z R
n La componente directa se mide con la ayuda A
de tres transformadores de corriente (TC) según
se indica en el esquema de la figura 37.
El transformador auxiliar T2 genera una
corriente proporcional a (I3 - I2) que circula a Fig. 36.
través de R.
Cuaderno Técnico Schneider n° 018 / p. 30

31. 1
V1
1
V1
2 V2
2 V2
3
V3
3
V3
T1 T2
T1 T2
1 3 3 2
1 3 3 2
Z
Z R
R
R/2 R 3/2
R 3 /2 R/2
V
V
Fig. 37. Fig. 38.
n La componente inversa se mide también con 1 1
la ayuda de tres transformadores de corriente
2 2
conectados según el esquema de la figura 38.
Con idéntico razonamiento al caso anterior se
3 3
deduce que la tensión en los bornes del
voltímetro es proporcional a:
( )
I1 − I3 + ( I3 − I2 ) − a2
A
= I1 − a . I2 − I3
2
(a + 1)
2
= I1 + a2. I2 + a. I3 = 3 I i
Fig. 39.
n La componente homopolar es igual a un
tercio de la corriente de neutro que circula
directamente por la conexión de puesta a tierra
(neutro distribuido).
Tres transformadores puestos en paralelo
permiten su medida en el amperímetro A
I1 + I2 + I3 = Ih (figura 39).
Un transformador toroidal abrazando la totalidad
de conductores activos permite la medida
anterior por la suma vectorial de las corrientes
de fase.
Cuaderno Técnico Schneider n° 018 / p. 31