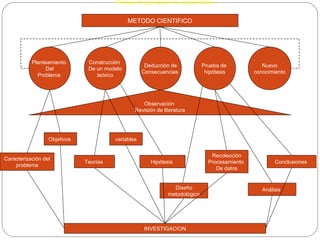
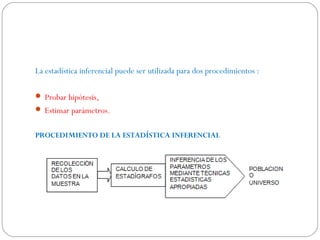
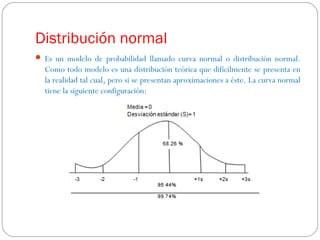
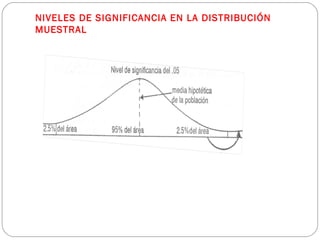
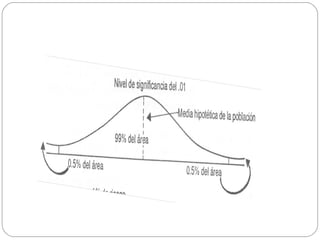
Este documento describe los conceptos fundamentales de la investigación científica y la estadística inferencial. Explica que la ciencia utiliza métodos sistemáticos como la teoría, el método y la técnica para explicar y transformar el mundo. Luego describe los diferentes tipos de métodos de investigación como inductivo, deductivo, experimental y otros. Finalmente, introduce los conceptos clave de la estadística inferencial como la prueba de hipótesis, los intervalos de confianza, las distribuciones muestrales y el nivel de significancia.

1. Estadistica

2. La investigación científica y la inferencia estadística.

3. TEMA 1: La investigación científica y la inferencia
estadística.
 CIENCIA: “Conjunto sistemático de conocimientos con los cuales, al establecer
principios y leyes universales, el hombre explica, describe y transforma el
mundo que lo rodea”.
 Tiene exigencia de método.
 CONOCIMIENTO CIENTICO Y CONOCIMIENTO COTIDIANO
 TEORÍA: “Conjunto de proposiciones que tiene como fin la explicación y
predicción de las conductas en un área determinada de fenómenos”
 La ciencia se expresa a través de la teoría: formulaciones, hipótesis y leyes
relacionadas.
 Hipótesis de menor y mayor generalidad: relacionados por leyes

4.  MÉTODO: “Procedimiento que se usa en la investigación científica, y que
constituye en el conjunto de postulados, principios, operaciones y reglas que
orientan a la investigación para alcanzar soluciones a cada problema del
conocimiento”.
 Método condicionado por la naturaleza del objeto
 METODOLOGIA: “Es el conocimiento de la unidad de los diversos métodos
con los cuales buscamos conocer a un mismo objeto. O sea mientras el método
es la sucesión de pasos, la metodología es el conocimiento de esos pasos.”
 TECNICA: “Conjunto de instrumentos y medios a través de los cuales se
efectúa el método”.
Las técnicas permiten manejar tanto al objeto, cuanto a la información que de
él se obtenga. Técnicas in-put y out-put
La técnica expresa el vínculo a través de la práctica, entre el conocimiento y los
métodos con el fenómeno al que se quiere investigar.
La ciencia esta conformada por la teoría, el método y la
técnica.

5. INVESTIGACIÓN: “La investigación es un proceso que consiste
en la búsqueda de nuevos conocimientos con el propósito de
encontrar la verdad o falsedad de conjeturas y coadyuvar al
desarrollo de la ciencia, poniendo en práctica el método
científico, es decir cumpliendo rigurosamente diversos pasos o
etapas en la búsqueda de esa verdad”.
La investigación científica busca en el objeto, en la materia en
movimiento, sus nexos causales, sus características esenciales, sus
expresiones genéricas y universales, las determinaciones
cuantitativas y cualitativas, lo necesario; es decir, en definitiva, las
leyes que rigen a la materia, tanto como leyes especiales, cuanto
como leyes generales.

6. TECNOLOGIA: “Conjunto de conocimientos de base
científica que permiten describir, explicar, diseñar y
aplicar soluciones técnicas a problemas prácticos de
forma sistemática y racional”.
La investigación tecnológica o aplicada se ocupa de
problemas prácticos, utilitarios, pero con un fondo
eminentemente científico, y con la ayuda de los métodos
de la investigación científica

7. Proceso de generación de conocimientos
METODO CIENTIFICO
Planteamiento
Del
Problema
Deducción de
Consecuencias
Construcción
De un modelo
teórico
Nuevo
conocimiento
Prueba de
hipótesis
Observación
Revisión de literatura
Caracterización del
problema
Objetivos
Teorías
variables
Hipótesis
Recolección
Procesamiento
De datos
Conclusiones
Diseño
metodológico
Análisis
INVESTIGACION

8. Clasificación de los métodos de investigación:
Categorías
Métodos
Genéricos, lógicos o generales
·Inductivo
·Deductivo
·Analítico
·Sintético
Específicos o particulares
·Experimentales
·Casi-experimentales
·No-experimentales

9. MÉTODO INDUCTIVO
Experiencia como punto de partida para la generación
del conocimiento. Parte de la observación de la realidad
para mediante la generalización de dicha observación
llegar a formular la ley.
(De lo particular a lo general)

10. MÉTODO DEDUCTIVO
Parte de la ley general y deduce consecuencias lógicas
aplicables a la realidad.
Va de lo general a lo particular.

11. Método Analítico (R. Descartes)
Dividir el problema en unidades, dividir lo complejo en
naturalezas simples. Se aspira a llegar de un proceso
complejo a sus verdades primeras o raíces del problema.
Método Sintético
Reconstruir en forma ordenada, de lo simple a lo
complejo, de lo particular a lo general, de las evidencias
más simples a las más complejas. Reconstrucción total
del objeto de conocimiento

12. MÉTODO HIPOTÉTICO-DEDUCTIVO
Mezcla los dos anteriores.
Enfatiza el hecho de que en el proceso de
adquisición de nuevos conocimientos la ciencia
actúa de ambas formas y las dos son partes de un
único método.
El investigador necesita ir de los datos a la teoría
y de la teoría a los datos.

13. Método experimental
Es muy utilizado en el campo de las ciencias naturales en
el estudio de hechos o fenómenos en los cuales el
investigador tiene un control de la situación a indagarse.
En un experimento se manipulan deliberadamente una o
más variables independientes (supuestas causas), para
analizar las consecuencias de esa manipulación sobre una
o más variables dependientes (supuestos efectos) en una
situación controlada por el investigador.
Para que un experimento sea considerado como tal debe
cumplir con los siguientes requisitos:

14. REQUISISTOS :
Que se pueda manipular intencional o deliberadamente a
la variable independiente( dar diferentes valores)
Que se pueda realizar el proceso de aleatorización al
conformar los grupos experimentales y asignar los
tratamientos.
Que sea posible medir el efecto de la variable
independiente sobre la dependiente.
Que exista control, o validez interna del proceso
experimental
Que se disponga de un grupo de comparación, control o
testigo

15. DISEÑOS EXPERIMENTALES DE INVESTIGACION
Con el propósito de responder a las preguntas de
investigación planteadas y someter a prueba las hipótesis
formuladas se selecciona un diseño especifico.
Los diseños pueden ser experimentales o no
experimentales.
En los diseños experimentales hay varios autores que
distinguen tres categorías generales: preexperimentales,
cuasi experimentales y experimentales verdaderos.

16. DISEÑOS PREEXPERIMENTALES
Presentan el más bajo control de las variables y no se
realiza asignación aleatoria de los sujetos al experimento.
El investigador no ejerce ningún control sobre las
variables extrañas o intervinientes, no hay grupo de
control. Por ejemplo:
Diseño de un caso único
Diseño de un grupo con medición (prueba) previa y
posterior.

17. DISEÑOS CUASIEXPERIMENTALES
Se ejerce también poco o ningún control sobre las variables
que intervienen.
Estos diseños usualmente se utilizan para grupos ya
constituidos. Por ejemplo:
Diseños de un grupo con medición antes y después.
Diseño con grupo de comparación equivalente.

18. Los diseños cuasiexperimentales manipulan
deliberadamente al menos una variable
independiente para ver su efecto u relación con
una o más variables dependientes.
En los diseños cuasi experimentales los sujetos
no son asignados al azar a los grupos ni
emparejados; sino que dichos grupos ya estaban
formados antes del experimento, son grupos
intactos

19. Los diseños cuasi- experimentales siguen los
mismos procedimientos de los experimentales
verdaderos, con la particularidad de que los
sujetos o unidades experimentales no son
asignados aleatoriamente a los grupos de
experimentación o tratamientos a aplicarse, con
lo cual no se tiene un control total sobre la
situación u problema a investigarse.

20. DISEÑOS EXPERIMENTALES VERDADEROS
Diseños con medición previa y posterior con
grupo de control.
Diseños con medición previa y grupo de control.
Diseño de series cronológicas
Diseños factoriales entre otros.

21. DEFINICION DEL TIPO DE INVESTIGACIÓN A
REALIZAR
Para nuestros propósitos se consideran básicamente cuatro tipos
de investigación:
EXPLORATORIOS
DESCRIPTIVOS
CORRELACIONALES
EXPLICATIVOS
De acuerdo al tipo de estudio a emplear, varía la estrategia de
investigación.
El diseño, los datos que se recolectan, la manera de obtenerlos, el
muestreo y otros componentes del proceso de investigación son
distintos en estudios exploratorios, descriptivos, correlaciónales y
explicativos.

22. TEMA
ASPECTOS GENERALES DE LA
ESTADISTICA INFERENCIAL
¿Para qué es útil la estadística inferencial?

23. Frecuentemente, el propósito de la investigación va más allá de describir las
distribuciones de las variables: se pretende generalizar los resultados
obtenidos en la muestra a la población o universo.
Los datos casi siempre son recolectados de una muestra y sus resultados
estadísticos se denominan "estadígrafos ", la media o la desviación estándar
de la distribución de una muestra son estadígrafos.
A las estadísticas de la población o universo se les conoce como
"parámetros". Los parámetros no son calculados, porque no se recolectan
datos de toda la población, pero pueden ser inferidos de los estadígrafos, de
ahí el nombre de "estadística inferencial.

24. La estadística inferencial puede ser utilizada para dos procedimientos :
 Probar hipótesis,
 Estimar parámetros.
PROCEDIMIENTO DE LA ESTADÍSTICA INFERENCIAL

25. Estimación de parametros:Intervalo de
confianza
 Un procedimiento de la estadística inferencial es construir un intervalo donde
se localiza un parámetro . Por ejemplo, en lugar de pretender probar una
hipótesis acerca de la media poblacional, puede buscarse obtener un intervalo
donde se ubique dicha media. Esto requiere un nivel de confianza. El nivel de
confianza es al intervalo de confianza lo que el nivel de significancia es a la
prueba de hipótesis. Es decir, el nivel de confianza es una probabilidad definida
de que un parámetro se va a ubicar en un determinado intervalo.

26. ¿En qué consiste la prueba de hipótesis?
Una hipótesis en el contexto de la estadística
inferencial es una proposición respecto a uno o
varios parámetros, y lo que el investigador hace a
través de la prueba de hipótesis es determinar si la
hipótesis es consistente con los datos obtenidos en
la muestra.
Para comprender lo que es la prueba de hipótesis en
la estadística inferencial es necesario revisar el
concepto de distribución muestral y nivel de
significancia.

27. ¿Qué es una distribución muestral?
 Una distribución muestral -consiste en un conjunto de valores sobre una
estadística (Ej.: la media) calculada de todas las muestras posibles de un
determinado tamaño
 Rara vez se obtiene la distribución muestral (la distribución de las medias de
todas las muestras posibles). Es más bien un concepto teórico definido por la
Estadística para los investigadores. Lo que los investigadores hacen es extraer
una sola muestra.
 Teorema central del límite: "Si una población (no necesariamente normal)
tiene de media U y de desviación estándar a (s ), la distribución de las medias
en el muestreo aleatorio realizado en esta población tiende, al aumentar n, a
una distribución normal de media y desviación estándar

28. Distribución normal
 Es un modelo de probabilidad llamado curva normal o distribución normal.
Como todo modelo es una distribución teórica que difícilmente se presenta en
la realidad tal cual, pero si se presentan aproximaciones a éste. La curva normal
tiene la siguiente configuración:

29. Las características de la distribución normal son:
 Es unimodal,
 La asimetría es cero. La mitad de la curva es exactamente igual a la otra mitad. La
distancia entre la media y +3s es la misma que la distancia entre la media y +3s s la
misma que a la distancia entre la media y -3s.
 La base está dada en unidades de desviación estándar (puntuaciones "z"), destacando
las puntuaciones —1s, —2s, —3s, +1s, +2s y +3s (que equivalen respectivamente
a — 1.00z, —2.00z, —3.00z, +1.00z, +2.00z y +3.00z). Las distancias entre
puntuaciones "z" representan áreas bajo la curva. De hecho, la distribución de
puntuaciones "z" es la curva normal.
 Es mesocúrtica (curtosis de cero).
 La media, la mediana y la moda coinciden en el mismo punto.

30. ¿Qué es el nivel de significancia?
Para probar hipótesis inferenciales respecto a la media,
el investigador tiene que evaluar si la probabilidad de que
la media de la muestra esté cerca de la media de la
distribución muestral es grande o pequeña. Si es
pequeña, el investigador dudará de generalizar a la
población. Si es grande, el investigador podrá hacer
generalizaciones. Es aquí donde entra el nivel de
significancia o nivel alfa . Éste es un nivel de probabilidad
de equivocarse y se fija antes de probar hipótesis
inferenciales.

31. Se acudirá a un ejemplo coloquial para ejemplificarlo y
luego explicarlo:
Si usted fuera a apostar en las carreras de caballos y
tuviera 95% de probabilidades de atinarle al ganador,
contra sólo un 5% de perder, ¿apostaría? Seguramente sí,
siempre y cuando le aseguraran ese 95% en su favor, o si le
dieran 95 boletos de 100 para la rifa de un automóvil,
¿tendría confianza en que va a estrenar vehículo?
Seguramente sí. No tendría la certeza total, ésta no existe
en el universo, al menos para los seres humanos.

32. algo similar hace el investigador. Él obtiene una estadística en una
muestra (ej: la media) y analiza qué porcentaje tiene de confianza
de que dicha estadística se acerque al valor de la distribución
muestral (que es el valor de la población o parámetro). Busca un
alto porcentaje de confianza, una probabilidad elevada para estar
tranquilo. Porque sabe que puede haber error de muestreo, y
aunque la evidencia parece mostrar una aparente "cercanía" entre
el valor calculado en la muestra y el parámetro, esta "cercanía"
puede no ser real y deberse a errores en la selección de la
muestra.

33. ¿Y con qué porcentaje tiene confianza el investigador para
generalizar? Existen dos niveles convenidos :
El nivel de significancia del .05, el cual implica que el
investigador tiene 95% de seguridad para generalizar sin
equivocarse, y sólo un 5 % en contra. En términos de
probabilidad, 0.95 y .05 respectivamente, ambos suman
la unidad.
El nivel de significancia del 01, el cual implica que el
investigador tiene un 99% en su favor para generalizar
sin temor y un 1% en contra (0.99 y 0.01=1.00).

34. NIVELES DE SIGNIFICANCIA EN LA DISTRIBUCIÓN
MUESTRAL

36. ¿Se pueden cometer errores al realizar estadística
inferencial?
 Nunca podemos estar completamente seguros de nuestra estimación.
Trabajamos con altos niveles de confianza o seguridad y aunque el riesgo es
mínimo, podría cometerse un error. Los resultados posibles al probar hipótesis
pueden ser.
1) Aceptar una hipótesis verdadera (decisión correcta).
2) Rechazar una hipótesis falsa (decisión correcta).
3) Aceptar una hipótesis falsa (error conocido como del Tipo II o beta).
4) Rechazar una hipótesis verdadera (error conocido como de Tipo I o error
alfa).

37. Ambos tipos de error son indeseables y puede reducirse la
posibilidad de que se presenten mediante:
a) Muestras representativas probabilísticas.
b) Inspección cuidadosa de los datos.
c) Selección de las pruebas estadísticas apropiadas.
d) Mayor conocimiento de la población.