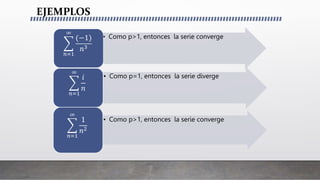
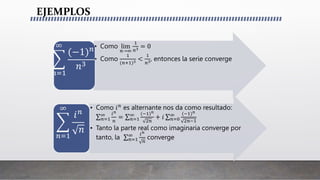
Este documento presenta criterios para determinar si una serie compleja converge o diverge. Introduce el teorema del límite, que establece que una serie converge solo si el límite de sus términos es cero. También define series tipo p, que convergen si p es mayor que 1, y series alternantes, que convergen si el límite de sus términos es cero y cada término es menor que el siguiente. Finalmente, presenta criterios de comparación y razón para determinar la convergencia basados en comparar una serie con otra o en el límite de la razón entre t

1. CONVERGENCIA
SERIES COMPLEJAS
DIANA PAOLA GÓMEZ
MATEMÁTICAS ESPECIALES

2. CRITERIO PARA LA CONVERGENCIA
TEOREMA 1 (del limite): Si una serie 0
∞
𝑧𝑛 es
convergente entonces lim
𝑛→∞
𝑧𝑛 = 0. Por tanto, si el
lim
𝑛→∞
𝑧𝑛 ≠ 0 entonces la serie es divergente.
NOTA: con este teorema se debe tener cuidado, pues sirve para verificar si una serie es
divergente cuando lim
𝑛→∞
𝑧𝑛 ≠ 0 , pero no cuando lim
𝑛→∞
𝑧𝑛 = 0 no se puede decir nada.

3. EJEMPLO
lim
𝑛→∞
1 +
𝑖
𝑛
= 1 + 0 = 1
lim
𝑛→∞
1 +
𝑖
𝑛
= 1 ≠ 0 entonces
1
∞
(1 +
𝑖
𝑛
) diverge
Considere la serie 1
∞
(1 +
𝑖
𝑛
), ¿es convergente o divergente?

4. EJEMPLOS
• Como el lim
𝑛→∞
3𝑖 + 𝑛 = 3𝑖 + ∞ = ∞
• Entonces como ∞ ≠ 0 entonces la serie diverge
𝑛=0
∞
(3𝑖 + 𝑛)
• Como el lim
𝑛→∞
𝑖
𝑛
= 0, en este caso no se puede
establecer convergencia.
• Mas adelante se establece que diverge
𝑛=1
∞
𝑖
𝑛
• Como el lim
𝑛→∞
1
𝑛2 = 0, en este caso no se
puede establecer convergencia.
• Mas adelante se establece que converge
𝑛=1
∞
1
𝑛2

5. CRITERIO PARA LA CONVERGENCIA
DEFINICIÓN 1: Series tipo p, una serie de la forma
𝑛=1
∞ 1
𝑛𝑝 es convergente si 𝑝 > 1 , si 𝑝 ≤ 1 entonces la
serie es divergente.

6. EJEMPLOS
• Como p>1, entonces la serie converge
𝑛=1
∞
(−1)
𝑛3
• Como p=1, entonces la serie diverge
𝑛=1
∞
𝑖
𝑛
• Como p>1, entonces la serie converge
𝑛=1
∞
1
𝑛2

7. CRITERIO PARA LA CONVERGENCIA
TEOREMA 2: Series alternantes, si la serie tiene la forma
𝑛=0
∞
(−1)𝑛𝑏𝑛. Si cumple las siguientes condiciones se
dice que converge:
1. lim
𝑛→∞
𝑏𝑛 = 0
2. 𝑏𝑛+1 ≤ 𝑏𝑛

8. EJEMPLOS
• Como lim
𝑛→∞
1
𝑛3 = 0
• Como
1
(𝑛+1)3 <
1
𝑛3, entonces la serie converge
𝑛=1
∞
(−1)𝑛
𝑛3
• Como 𝑖𝑛 es alternante nos da como resultado:
𝑛=1
∞ 𝑖𝑛
𝑛
= 𝑛=1
∞ (−1)𝑛
2𝑛
+ 𝑖 𝑛=0
∞ (−1)𝑛
2𝑛−1
• Tanto la parte real como imaginaria converge por
tanto, la 𝑛=1
∞ 𝑖𝑛
𝑛
converge
𝑛=1
∞
𝑖𝑛
𝑛

9. CRITERIO PARA LA CONVERGENCIA
TEOREMA 3(comparación): dada una serie de 𝑛=0
∞
𝑧𝑛 términos
complejos, si existe una serie 𝑛=0
∞
𝑎𝑛 de términos positivos, se
pueden dar:
1. Si 𝑛=0
∞
𝑎𝑛 es convergente y se cumple que 𝑎𝑛 ≥ 𝑧𝑛 , entonces
𝑛=0
∞
𝑧𝑛 es convergente.
2. Si 𝑛=0
∞
𝑎𝑛 es divergente y se cumple que 𝑎𝑛 ≤ 𝑧𝑛 , entonces
𝑛=0
∞
𝑧𝑛 es divergente.

10. CRITERIO PARA LA CONVERGENCIA
TEOREMA 4(criterio de la razón): dada una serie de 𝑛=0
∞
𝑧𝑛
términos complejos distintos de cero, supongamos:
lim
𝑛→∞
𝑧𝑛+1
𝑧𝑛
= 𝐿
1. Si L < 1 , entonces 𝑛=1
∞
𝑧𝑛 es convergente.
2. Si L > 1 , entonces 𝑛=1
∞
𝑧𝑛 es divergente.
3. Si L = 1 , entonces el criterio no puede establecer
convergencia o divergencia