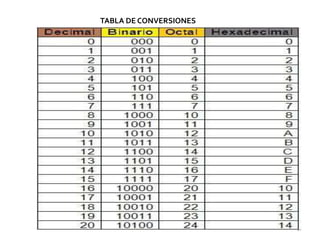
Este documento describe los sistemas numéricos binario, decimal, octal y hexadecimal. Explica que cada sistema tiene una base y conjuntos de dígitos diferentes. Luego detalla operaciones como suma, resta, multiplicación y división en el sistema binario, incluyendo ejemplos. Finalmente, cubre la conversión entre las bases binaria, octal y hexadecimal.

2. SISTEMAS NUMERICOS
Conjunto ordenado de símbolos llamados “dígitos”, con relaciones definidas para
operaciones de :
Suma , Resta, Multiplicación y División
La base (r) del sistema representa el número total de dígitos permitidos, por
ejemplo:
r=2 Binario dígitos: 0,1
r=10 Decimal dígitos: 0,1,2,3,4,5,6,7,8,9
r=8 Octal dígitos: 0,1,2,3,4,5,6,7
r=16 Hexadecimal dígitos:0,1,2,3,4,5,6,7,8,9,
A,B,C,D,E,F
Conceptos de distributividad,
conmutatividad y asociatividad se usan
en todos los sistemas

3. TABLA DE CONVERSIONES

4. El término bit, es una abreviación de dígito binario, un dígito
binario es un estado “abierto” o “cerrado” lógico, se lo
comprende mostrándolo y analizándolo como un “1” o “0”. En
una computadora es representado un “1” o “0” eléctricamente
con diferencia de voltaje; en el caso de un Disco Rígido
(generalmente el Sistema de Almacenamiento Principal en una
PC), o CD, por dos formas distintas de diminutas marcas en la
superficie, en el caso del Disco Rígido señales magnéticas, en el
caso del CD señales que reflejarán el "láser" que rebotará en el
CD y será recepcionado por un sensor de distinta forma (debido
a que son hechas de tal forma que reboten distinto la luz),
indicando así, si es un cero o un uno.

5. SUMA EN BINARIO.
 Para aprender a sumar, se necesita específicamente La tabla
de sumar, en binario, es mucho más sencilla que en decimal.
Sólo hay que recordar cuatro combinaciones posibles:
Las sumas 0 + 0, 0 + 1 , 1 + 0 y 1+1 son evidentes:
0+0=0
0+1=1
1+0=1
1 + 1 = 0 ( lleva 1).

6.  010 + 101 = 111
 210 + 510 = 710
 001101 + 100101 = 110010
 1310 + 3710 = 5010
 1011011 + 1011010 = 10110101
 9110 + 9010 = 18110
 110111011 + 100111011 = 1011110110
 44310 + 31510 = 75810
SUSTRACCIÓN EN BINARIO
 La técnica de la resta en binario es, nuevamente, igual que la misma operación en el
sistema decimal. Pero conviene repasar la operación de restar en decimal para
comprender la operación binaria, que es más sencilla. Los términos que intervienen
en la resta se llaman. minuendo, sustraendo y diferencia.

7.  Las restas 0 - 0, 1 – 0,0-1 y 1 - 1 son evidentes:
0–0=0
1–0=1
1–1=0
0 – 1 = 0 (presta 1)
La resta 0 - 1 se resuelve, igual que en el sistema decimal, tomando una unidad prestada
de la posición siguiente: 10 - 1, es decir, 210 – 110 = 1. Esa unidad prestada debe devolverse,
sumándola, a la posición siguiente. Veamos algunos ejemplos:
 111 – 101 = 010
 710 – 510 = 210
 10001 – 01010 = 00111
 1710 – 1010 = 710
 11011001 – 10101011 = 00101110
 21710 – 17110 = 4610
 111101001 – 101101101 = 001111100
 48910 – 36510 = 12410

8.  La multiplicación en binario es más fácil que en cualquier otro
sistema de numeración. Como los factores de la multiplicación sólo pueden
ser CEROS o UNOS, el producto sólo puede ser CERO o UNO. En otras
palabras, las tablas de multiplicar del cero y del uno son muy fáciles de
aprender:
* 0 1
0 0 0
1 0 1
En un ordenador, sin embargo, la operación de multiplicar se realiza mediante
sumas repetidas. Eso crea algunos problemas en la programación porque cada
suma de dos UNOS origina un arrastre, que se resuelven contando el número
de UNOS y de arrastres en cada columna. Si el número de UNOS es par, la
suma es un CERO y si es impar, un UNO. Luego, para determinar los arrastres a
la posición superior, se cuentan las parejas de UNOS.

9. 3349 * 13 = 43537
¡correcto!
Para comprobar que el resultado es correcto, convertimos los
factores y el resultado al sistema decimal:
3349 * 13 = 43537
¡correcto!

10.  Igual que en el producto, la división es muy fácil de realizar, porque no son posibles en el
cociente otras cifras que UNOS y CEROS.
Consideremos el siguiente ejemplo, 42 : 6 = 7, en binario:
Se intenta dividir el dividendo por el divisor, empezando por tomar en ambos el mismo
número de cifras (100 entre 110, en el ejemplo). Si no puede dividirse, se intenta la
división tomando un dígito más (1001 entre 100).

12. Conversión entre Base Binaria y Hexadecimal
Base Binaria a Base Hexadecimal
( 1100 0011 1111 . 1101 )2 = ( C3F.D )16
C 3 F D
( 0001 1000 )2 = ( 18 )16
Completando
Con 0’s

13. Conversión entre Base Binaria y Hexadecimal
Base Base Hexadecimal a Base Binaria
( 4AB.F5 )16 = ( 0100 1010 1011 . 1111 0101 )2
Sistemas Digitales 13

14. Conversión entre Base Binaria y Octal
Base Binaria a Base Octal
( 010 000 111 111 . 110 100 )2 = ( 2077.64 )8
Completando
Con 0’s
Base Base Octal a Base Binaria
( 457.05 )8 = ( 100 101 111 . 000 101 )2
Sistemas Digitales 14

15. CONVERTIR DE HEXADECIMAL A BINARIO
AB4= |1010|1011|0100
CONVERTIR DE BINARIO A HEXADECIMAL
100111100011= 9D3