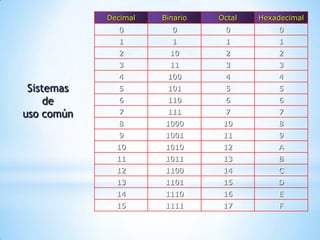
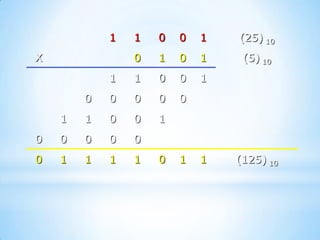
El documento resume los sistemas numéricos, incluyendo la notación posicional y polinómica, las conversiones entre bases binarias, octales y hexadecimales, y las operaciones aritméticas como suma, resta, multiplicación y división en el sistema binario. Explica cómo representar números en diferentes bases y cómo convertir entre ellas usando divisiones y multiplicaciones sucesivas.

1. Integrantes:
4to Nivel
Ibarra Milton.
Ing. Sistema
Macías María José.
Salazar Melanie.

2. SISTEMAS NUMERICOS
Conjunto ordenado de símbolos llamados
“dígitos”, con relaciones definidas para operaciones de
:
Suma , Resta, Multiplicación y División
La base (r) del sistema representa el número total de
dígitos permitidos, por ejemplo:
r=2 Binario dígitos: 0,1
r=10 Decimal dígitos: 0,1,2,3,4,5,6,7,8,9
r=8 Octal dígitos: 0,1,2,3,4,5,6,7
r=16Hexadecimal
dígitos:0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F

3. NOTACION POSICIONAL
En general, un número positivo puede
escribirse como:
Ejemplos
N= (an-1….a1a0a-1a-2….a-m)r (123.45)10
(1001.11)2
Donde: (763.12)8
* .= punto decimal (3A.2F)16
* r= base o decimal
* n= número de dígitos enteros positivos
* m= número de dígitos enteros negativos
* an-1= dígito más significativo (MSD)
* a-m= dígito menos significativo (LSD)

4. NOTACION POLINOMIAL
n 1
i
N ai r
i m
Ejemplos
(123.45)10 = 1*102+2*101+3*100+4*10-1+5*10-2
(1001.11)2 = 1*23+0*22+0*21+1*20+1*2-1+1*2-2
(763.12)8 = 7*82+6*81+3*80+1*8-1+2*8-2
(3A.2F)16 = 3*161+A*160+2*16-1+F*16-2
Donde: A=10, B=11, C=12, D=13, E=14 y F=15

5. Decimal Binario Octal Hexadecimal
0 0 0 0
1 1 1 1
2 10 2 2
3 11 3 3
4 100 4 4
Sistemas 5 101 5 5
de 6 110 6 6
uso común 7 111 7 7
8 1000 10 8
9 1001 11 9
10 1010 12 A
11 1011 13 B
12 1100 14 C
13 1101 15 D
14 1110 16 E
15 1111 17 F

6. Conversión de un sistema de Base “ r ” a Base “10”
Utilizando la notación polinomial:
Ejemplos:
(10100)2 = 1*24+0*23+1*22+0*21+0*20 =(20)10
(AF3.15)16 = 10*162+15*161+3*160+1*16-1+5*16-2 =
(2803.08203125)10

7. Conversión de un sistema de Base “ r ” a Base “10”
Utilizando la noción de los pesos:
Ejemplo en el sistema Binario (r = 2):
Peso (21) :8 4 2 1
Digito (bi) : b3 b2 b1 b0
(1001)2 = 8 + 1 = (9)10
(0101)2 = 4 + 1 = (5)10

8. Conversión de un sistema de Base “10” a Base “ r ”
Ejemplos de números enteros :
Utilizando divisiones sucesivas por la Base
msb = bit más significativo
(13)10 = (1101)2 (234)10 = (EA)16
13 : 2 234 :16
1 6 :2 10 14 :16
0 3 :2 A 14 0
1 1 :2 E
1 0

9. Conversión de un sistema de Base “10” a Base “ r ”
Ejemplos de números enteros y decimal. Sean los
números decimales 13.12510 y 234.2510
Utilizando divisiones sucesivas por la Base para la
parte entera (caso anterior) y multiplicaciones
sucesivas por la Base para la parte decimal.
entero entero
0.125 X2 0 25 X 16 4
0.250 X2 0 00 X 16 0
0.500 X2 1
1101.0012 EA.4016

10. Conversión de un sistema de Base “10” a Base “8”
Ejemplo : convertir (145.64)10 a número octal
Parte Entera : 14510= 2218
Entero Base Cuociente Resto
145 8 18 1
18 8 2 2
2 8 0 2

11. Conversión entre Base Binaria y Hexadecimal
Base Binaria a Base Hexadecimal
( 1100 0011 1111 . 1101 )2 = ( C3F.D )16
C 3 F D
1 8
( 0001 1000 )2 = ( 18 )16
COMPLETAMOS
CON 0

12. Conversión entre Base Binaria y Hexadecimal
Base Hexadecimal a Base Binaria
( 4AB.F5 )16 = ( 0100 1010 1011 . 1111 0101 )2
Base Octal a Base Binaria
( 457.05 )8 = ( 100 101 111 . 000 101 )2

13. Conversión entre Base Binaria y Octal
Base Binaria a Base Octal
( 010 000 111 111 . 110 100 )2 = ( 2077.64 )8
Completando
Completamos
Con 0’s
con 0

14. ARITMETICA BINARIA ( SUMA )
• Condiciones :
• 0+0=0
• 0+1=1
• 1+0=1
• 1 + 1 = 0 más un acarreo a la
siguiente posición más significativa.

15. SUMA BINARIA
0 1 0 1 1 1 (23)10
+ 0 0 1 0 1 0 (10)10
0 1 1 0 0 1 (25)10

16. 1 0 1 0 0 1 (41)10
+ 1 1 1 1 1 1 (63)10
1 0 1 1 0 0 0 (44)10

17. ARITMETICA BINARIA ( RESTA )
• Condiciones :
0-0=0
1-0=1
1-1=0
0 – 1 = 1 tomando prestado 1,
ó 10 – 1 = 1
La última regla señala que si se resta un bit 1 de un bit 0,
hay que tomar prestado un 1 de la siguiente columna más
significativa.

18. EJEMPLOS
1 21 20 20 1 20 (51)10
- 0 21 10 1 10 1 (21)10
1 0 1 1 0 1 (45)10

19. 1 1 0 1 1 1 (55)10
- 1 0 0 0 1 0 (34)10
0 1 0 1 0 1 (21)10

20. ARITMETICA BINARIA ( MULTIPLICACION)
• Ejemplo: Multiplicar 101112 por 10102
0 1 0 1 1 1 Multiplicando
X 1 0 1 0 Multiplicador
0 0 0 0 0
1 0 1 1 1
0 0 0 0 0
+
1 0 1 1 1
1 1 1 0 0 1 1 0 Producto

21. 1 0 1 1 0 (22)10
X 1 0 0 1 (9) 10
1 0 1 1 0
0 0 0 0 0
0 0 0 0 0
1 0 1 1 0
1 1 0 0 0 1 1 0 (198)10

22. 1 1 0 0 1 (25) 10
X 0 1 0 1 (5) 10
1 1 0 0 1
0 0 0 0 0
1 1 0 0 1
0 0 0 0 0
0 1 1 1 1 0 1 1 (125) 10

23. ARITMETICA BINARIA (DIVISION)
• Ejemplo: Dividir 11101112 entre 10012
5 5 4 1 Cociente
Divisor 1 0 0 1 1 1 1 0 1 1 1 Dividendo
1 0 0 1
1 0 1 1
1 0 0 1
1 0 1 1
1 0 0 1
1 0 Residuo

24. 1 1 1 1 Cociente
Divisor 1 0 0 1 1 1 1 0 1 1 1 Dividendo
1 0 0 1
1 0 1 1
1 0 0 1
1 0 1 1
1 0 0 1
1 0 Residuo