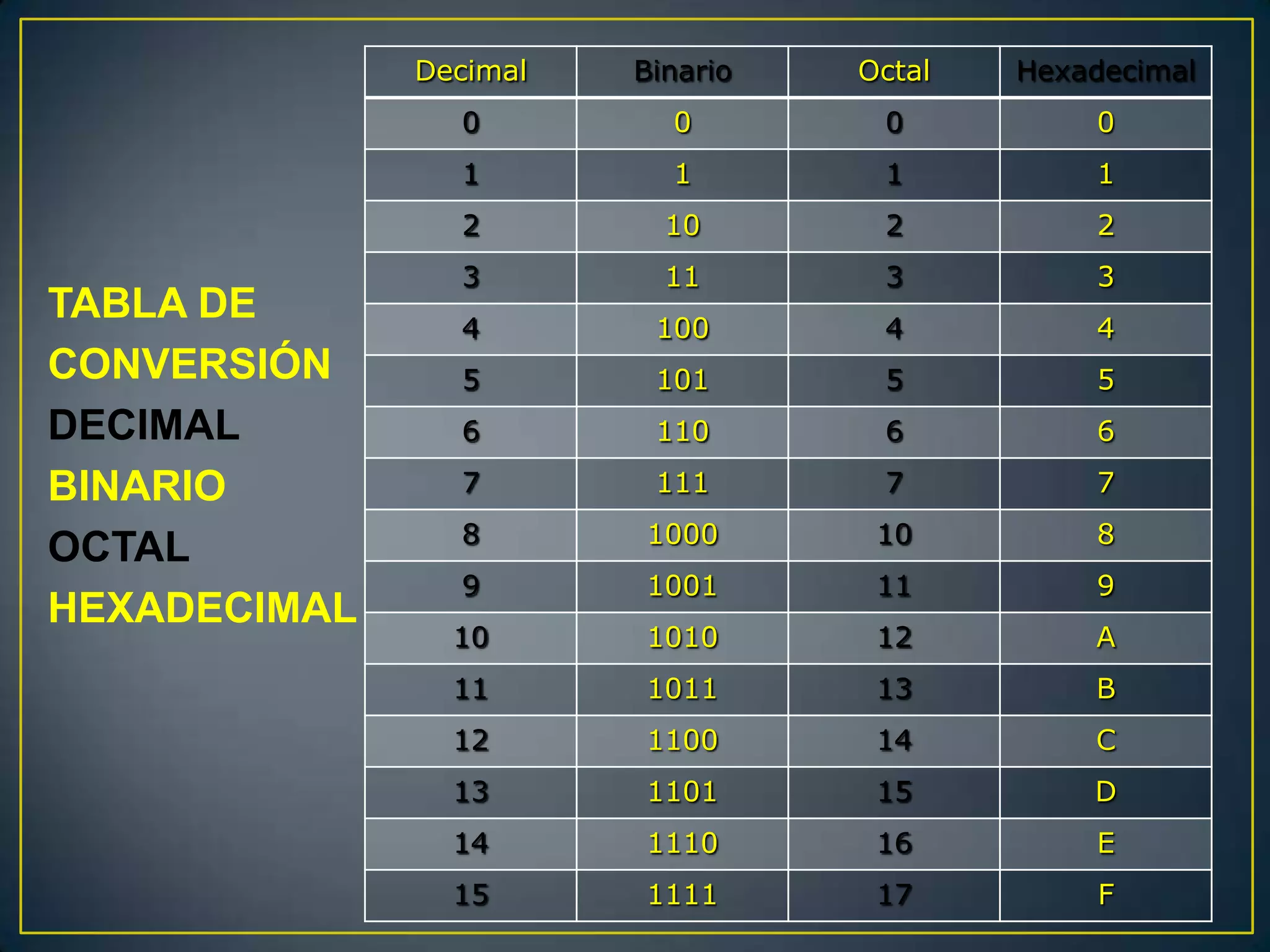
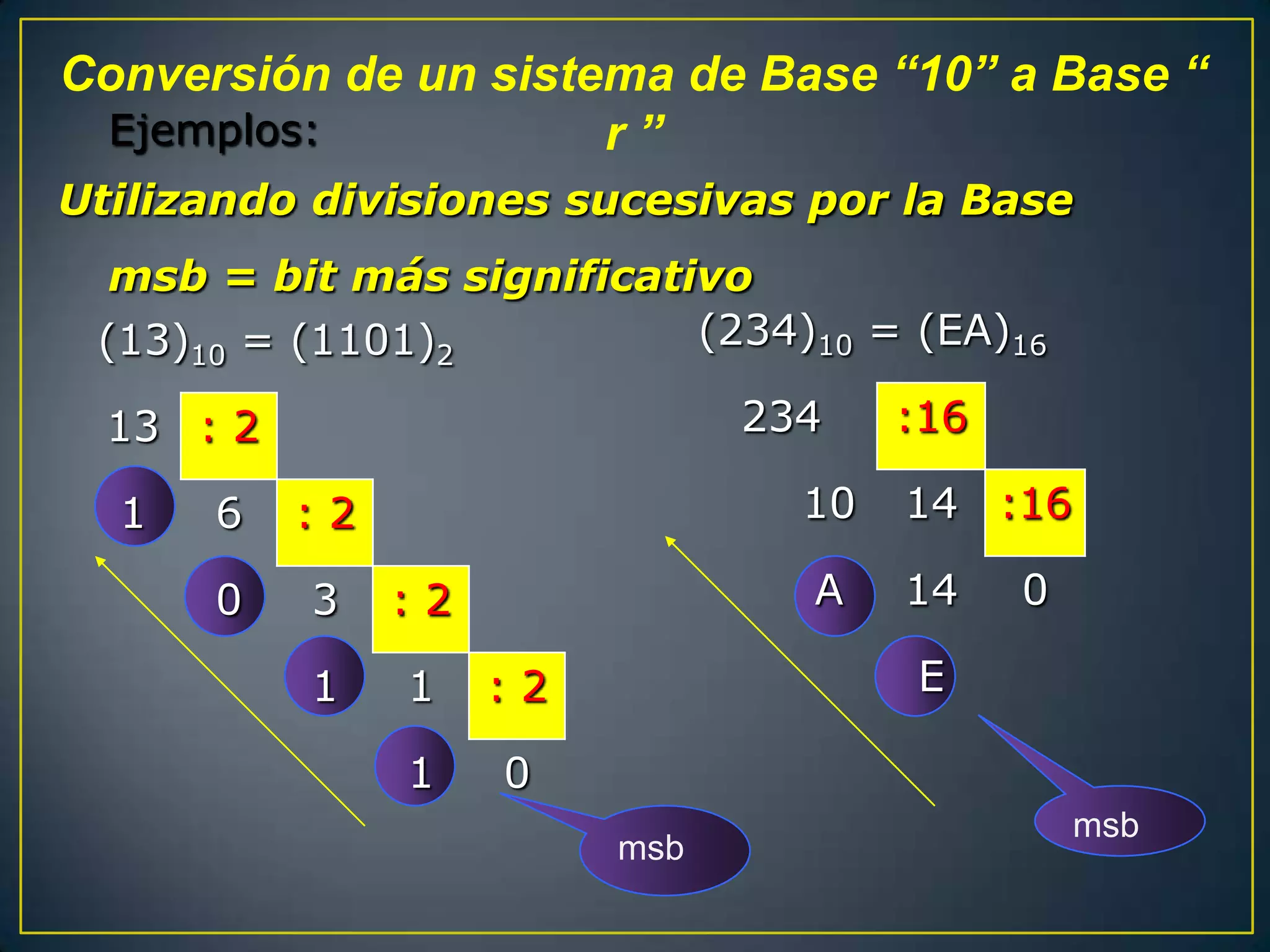
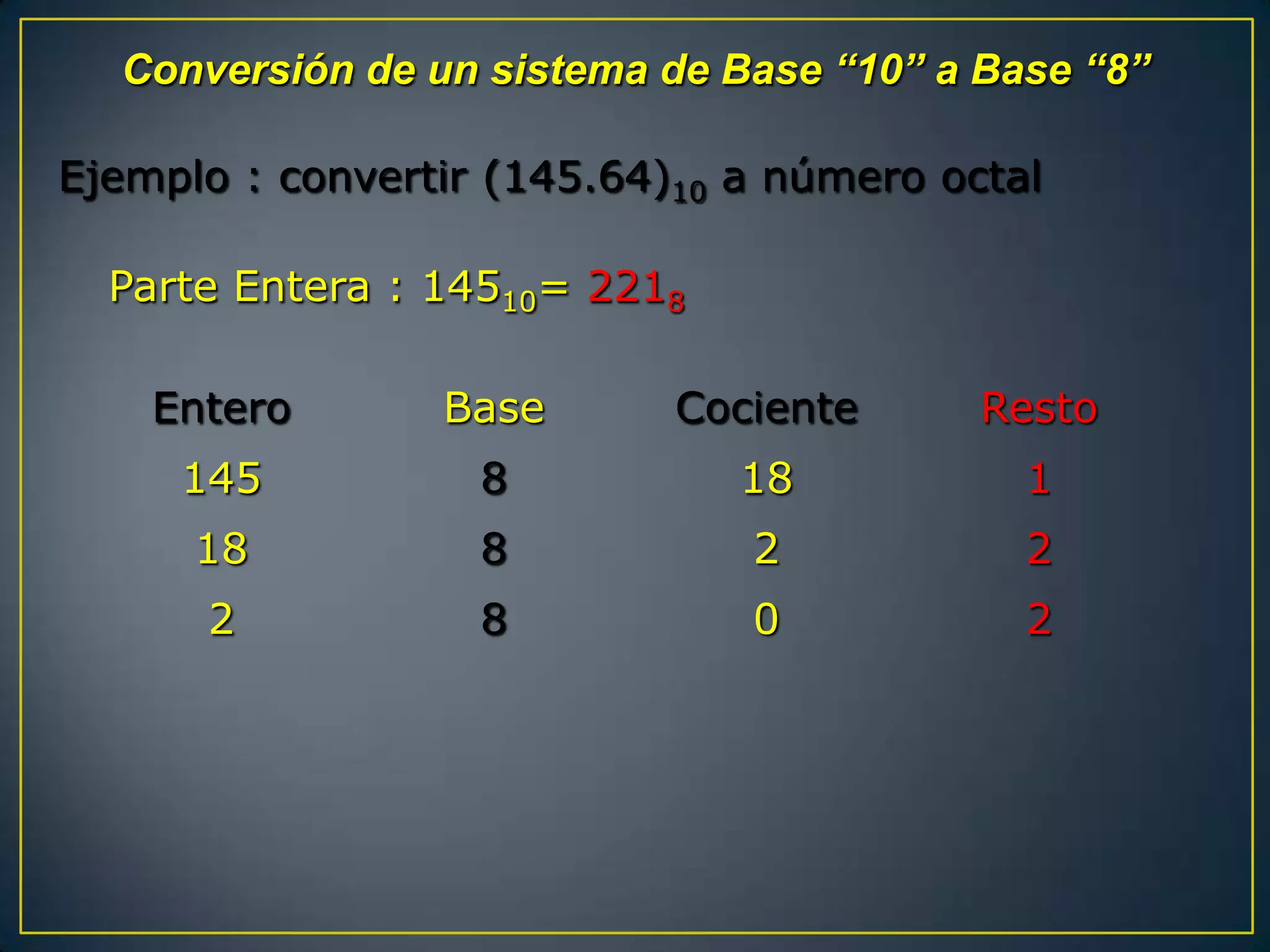
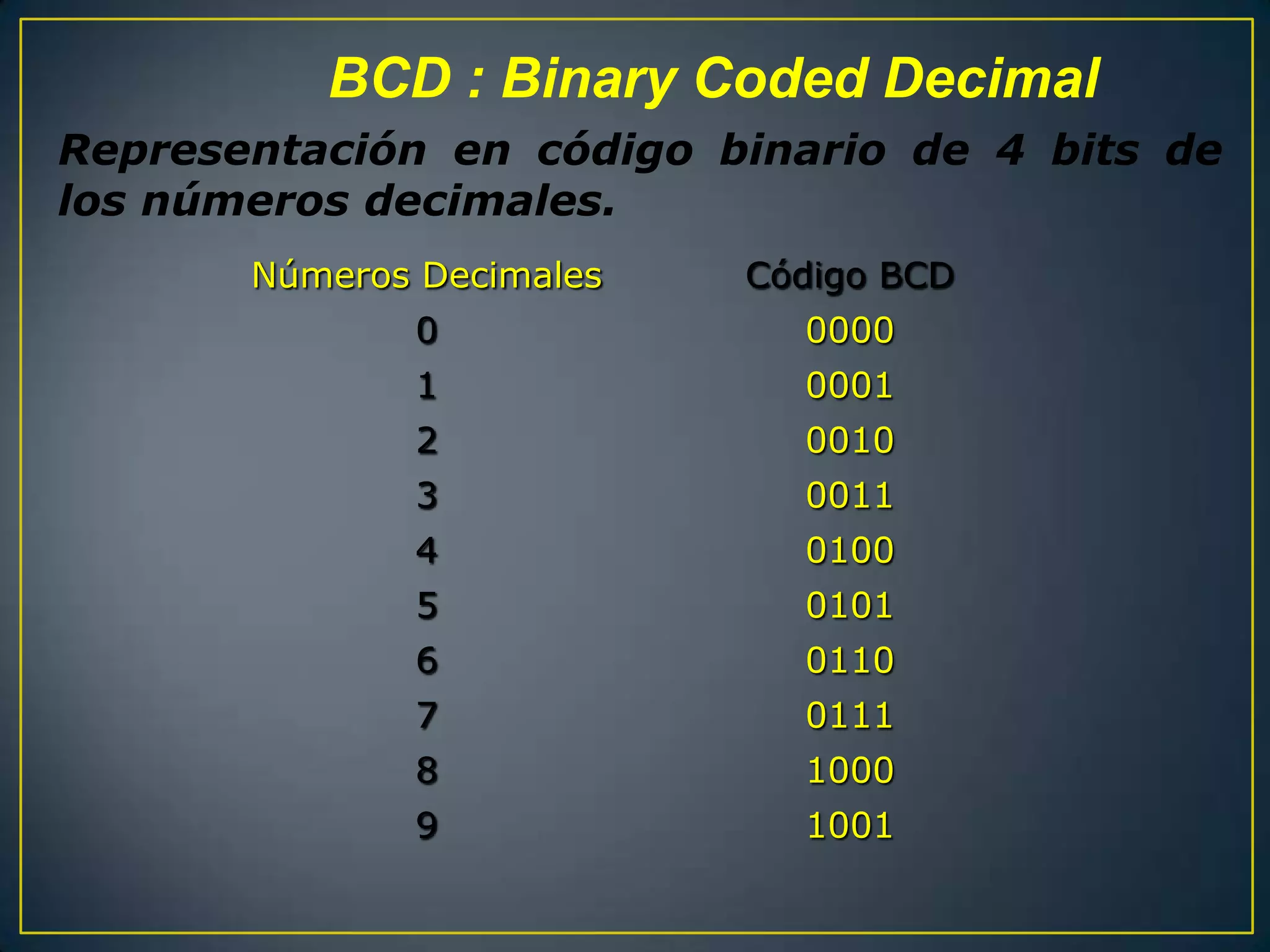
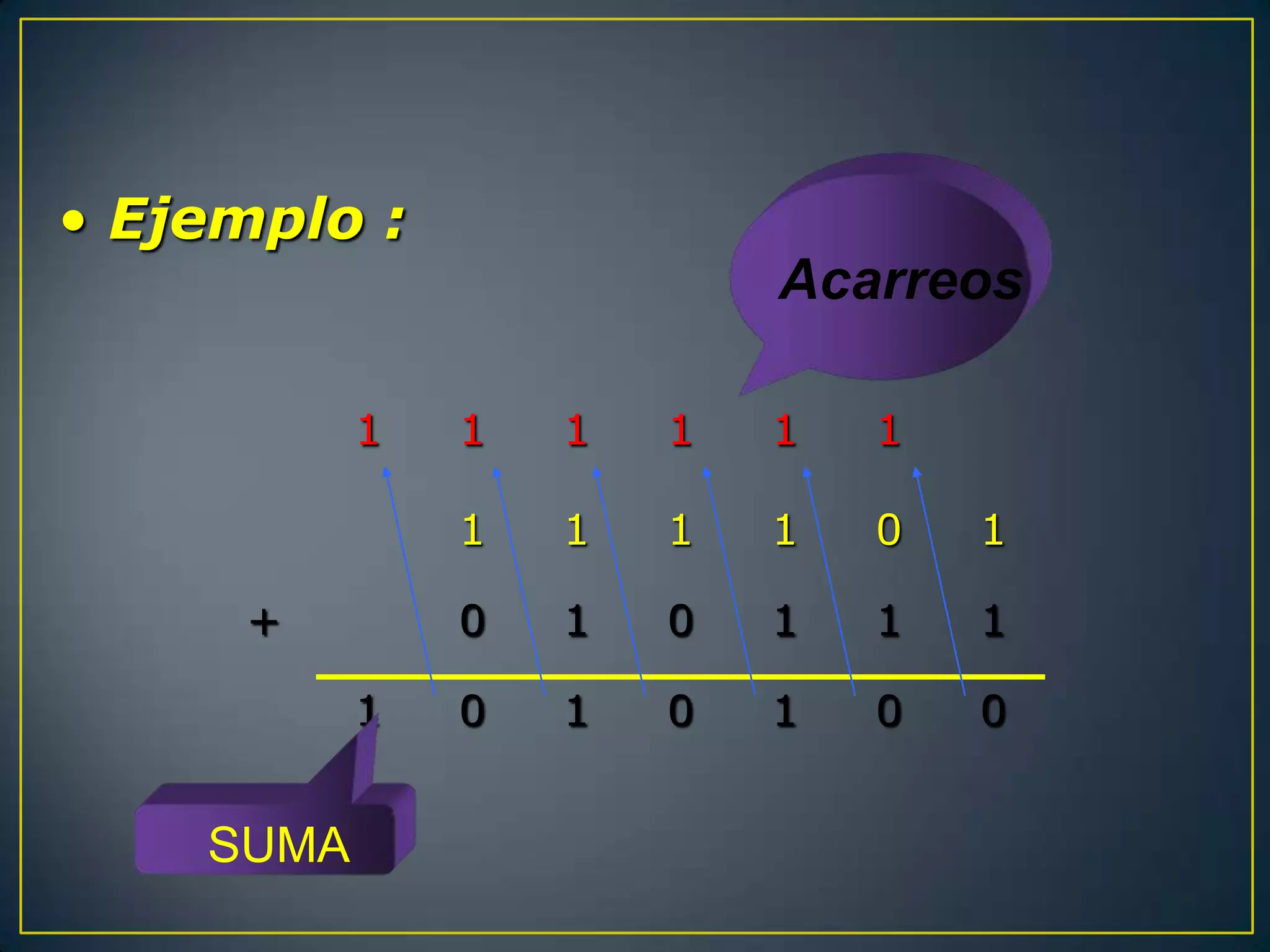
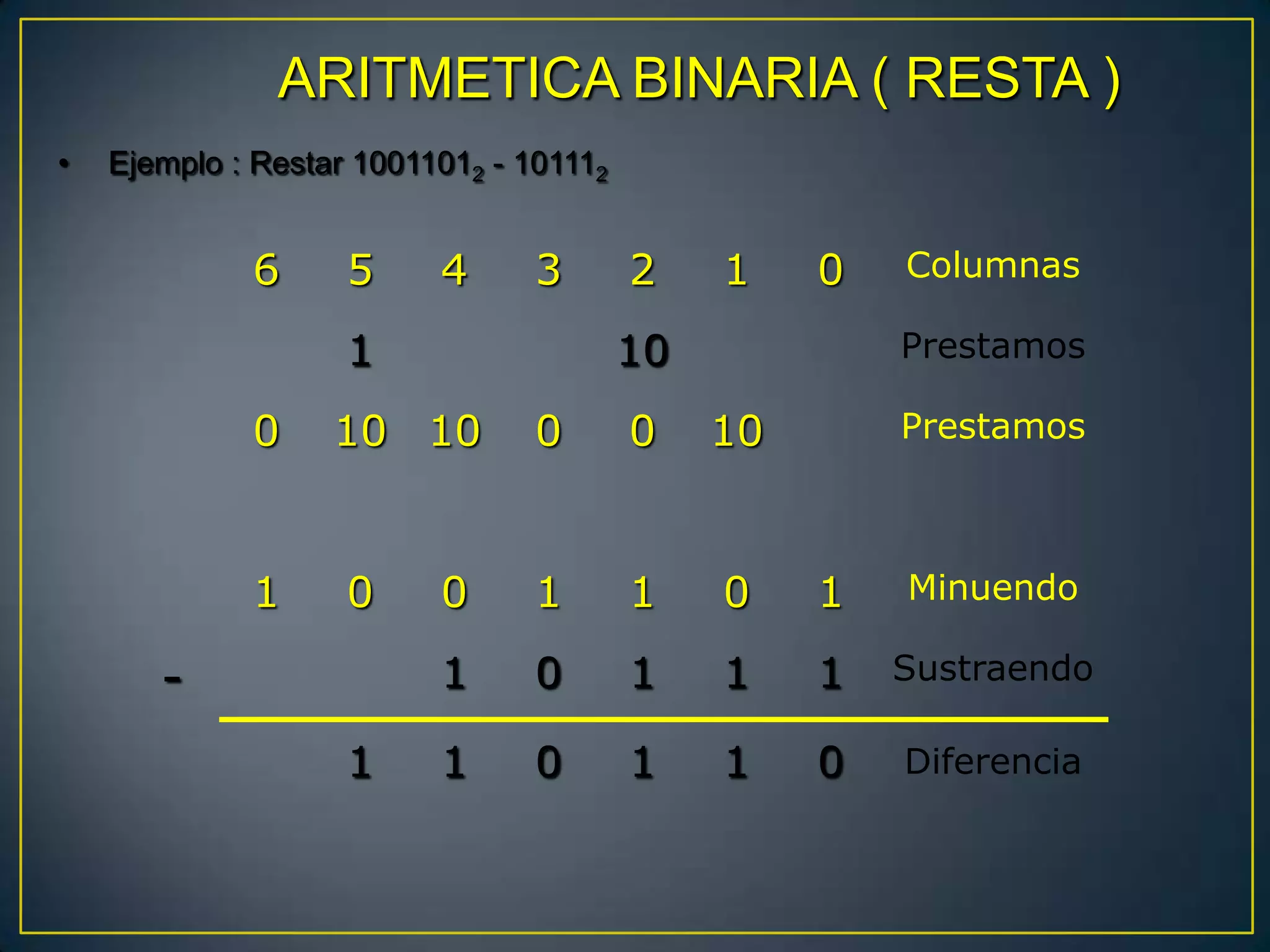
El documento presenta un trabajo grupal compuesto por tres integrantes que estudian el 4to semestre. Explica los sistemas numéricos binario, octal y hexadecimal, incluyendo tablas de conversión, representación BCD y operaciones aritméticas binarias como suma, resta, multiplicación y división.

1. TRABAJO GRUPAL:
INTEGRANTES:
 LOOR CEDEÑO CRISTHIAN XAVIER
 NAVARRETE DELGADO MARCOS
ANTONIO
 ZAMBRANO TENA VERONICA
JESSENIA
4TO SEMESTRE

2. • SISTEMAS NUMERICOS
Conjunto ordenado de símbolos llamados
“dígitos”, con relaciones definidas para operaciones
de :
Suma , Resta, Multiplicación y División
La base (r) del sistema representa el número total de
dígitos permitidos, por ejemplo:
r=2 Binario dígitos: 0,1
r=10 Decimal dígitos: 0,1,2,3,4,5,6,7,8,9
r=8 Octal dígitos: 0,1,2,3,4,5,6,7
r=16 Hexadecimal dígitos:0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F

3. n 1
i
N ai r
i m
Ejemplos
(123.45)10 = 1*102+2*101+3*100+4*10-1+5*10-2
(1001.11)2 = 1*23+0*22+0*21+1*20+1*2-1+1*2-2
(763.12)8 = 7*82+6*81+3*80+1*8-1+2*8-2
(3A.2F)16 = 3*161+A*160+2*16-1+F*16-2
Donde: A=10, B=11, C=12, D=13, E=14 y
F=15

4. Decimal Binario Octal Hexadecimal
0 0 0 0
1 1 1 1
2 10 2 2
3 11 3 3
TABLA DE 4 100 4 4
CONVERSIÓN 5 101 5 5
DECIMAL 6 110 6 6
BINARIO 7 111 7 7
8 1000 10 8
OCTAL
9 1001 11 9
HEXADECIMAL
10 1010 12 A
11 1011 13 B
12 1100 14 C
13 1101 15 D
14 1110 16 E
15 1111 17 F

5. CONVERSIÓN DE UN SISTEMA DE BASE “ R ” A BASE
“10”
Ejemplos:
• (10100)2 = 1*24+0*23+1*22+0*21+0*20 =(20)10
• (AF3.15)16 = 10*162+15*161+3*160+1*16-1
+5*16-2 = (2803.08203125)10

6. Conversión de un sistema de Base “ r ” a Base “10”
Ejemplo en el sistema Binario (r = 2):
Peso (21) :8 4 2 1
Digito (bi) : b3 b2 b1 b0
(1001)2 = 8 + 1 = (9)10
(0101)2 = 4 + 1 = (5)10

7. Conversión de un sistema de Base “10” a Base “
Ejemplos: r”
Utilizando divisiones sucesivas por la Base
msb = bit más significativo
(13)10 = (1101)2 (234)10 = (EA)16
13 : 2 234 :16
1 6 :2 10 14 :16
0 3 :2 A 14 0
1 1 :2 E
1 0
msb
msb

8. Conversión de un sistema de Base “10” a Base “8”
Ejemplo : convertir (145.64)10 a número octal
Parte Entera : 14510= 2218
Entero Base Cociente Resto
145 8 18 1
18 8 2 2
2 8 0 2

9. BCD : Binary Coded Decimal
Representación en código binario de 4 bits de
los números decimales.
Números Decimales Código BCD
0 0000
1 0001
2 0010
3 0011
4 0100
5 0101
6 0110
7 0111
8 1000
9 1001

10. BCD : Binary Coded Decimal
Ejemplo:
4 0 9 6
( 4096 )10 =0100 0000 1001 0110
Número decimal Representación BCD
Comparación con su representación en Base
binaria.
( 4096 )10 = ( 1000000000000 )2

11. ARITMETICA BINARIA ( SUMA )
• Condiciones :
• 0+0=0
• 0+1=1
• 1+0=1
• 1+1=0
más un acarreo a la siguiente posición más
significativa.

12. • Ejemplo :
Acarreos
1 1 1 1 1 1
1 1 1 1 0 1
+ 0 1 0 1 1 1
1 0 1 0 1 0 0
SUMA

13. ARITMETICA BINARIA (
• Condiciones : RESTA )
0-0=0
1-0=1
1-1=0
0 – 1 = 1 tomando prestado 1,
ó 10 – 1 = 1
La última regla señala que si se resta un bit 1 de un bit 0,
hay que tomar prestado un 1 de la siguiente columna más
significativa.

14. ARITMETICA BINARIA ( RESTA )
• Ejemplo : Restar 10011012 - 101112
6 5 4 3 2 1 0 Columnas
1 10 Prestamos
0 10 10 0 0 10 Prestamos
1 0 0 1 1 0 1 Minuendo
- 1 0 1 1 1 Sustraendo
1 1 0 1 1 0 Diferencia

15. ARITMETICA BINARIA ( MULTIPLICACION)
• Ejemplo: Multiplicar 101112 por 10102
1 0 1 1 1 Multiplicando
X 1 0 1 0 Multiplicador
0 0 0 0 0
1 0 1 1 1
0 0 0 0 0
+ 1 0 1 1 1
1 1 1 0 0 1 1 0 Producto

16. ARITMETICA BINARIA (DIVISION)
• Ejemplo: Dividir 11101112 entre 10012
1 1 0 1 Cuociente
Divisor 1 0 0 1 1 1 1 0 1 1 1 Dividendo
1 0 0 1
1 0 1 1
1 0 0 1
1 0 1 1
1 0 0 1
1 0 Residuo