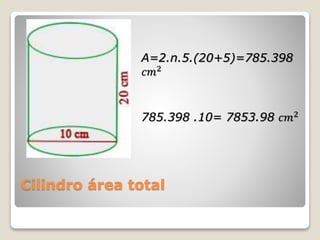
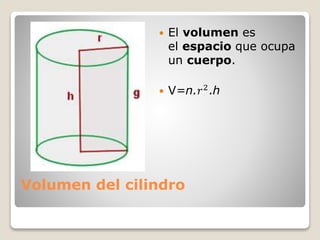
Los cuerpos geométricos son figuras tridimensionales clasificados en poliedros y cuerpos de revolución como conos y cilindros. Los conos se generan al rotar un triángulo rectángulo, mientras que los cilindros se forman por el desplazamiento de una línea recta sobre una curva cerrada. Se presentan fórmulas para calcular el área y volumen de estos cuerpos, destacando sus características geométricas.

1. Cuerpos geométricos
Un cuerpo geométrico es una figura
geométrica de tres dimensiones: largo, ancho y
alto.
Los cuerpos geométricos se clasifican en:
Poliedros
Los poliedros tiene las caras planas, están
limitados por polígonos.
Los poliedros pueden ser regulares e irregulares.

2. CONO
 El cono es un cuerpo
geométrico engendrado
por un triángulo
rectángulo al girar en
torno a uno de sus
catetos. Ver revolución
cono
 Podemos hallar el área
lateral , área
total y volumen de este
cuerpo geométrico,
utilizando las siguientes
formulas:

3. AREA TOTAL Y VOLUMEN DE CONO
ÁREA TOTAL
AT=AL+AB
(Es decir, el área
total es igual al área
lateral mas el área
del circulo de la
base)
 VOLUMEN
 V=Ab ° h/3
 (Es decir, el
volumen es igual
al área del
circulo de la base
multiplicado por la
altura ( h ) del
cono y dividido
entre 3)

4. Cilindro
 Si la directriz es
un círculo y la generatriz
es perpendicular a él,
entonces la superficie
obtenida, llamada cilindro
circular recto, será de
revolución y tendrá por lo
tanto todos sus puntos
situados a una distancia
fija de una línea recta,
el eje del cilindro. El sólido
encerrado por esta
superficie y por dos planos
perpendiculares al eje
también es llamado
cilindro. Este sólido es
utilizado como una
superficie Gausiana.
En geometría,
un cilindro es
una superficie de las
denominadas cuádricas for
mada por el desplazamiento
paralelo de
una recta llamada generatri
z a lo largo de una curva
plana, que debe ser
cerrada,
denominada directriz del
cilindro.

5. Cilindro área total
A=2.n.5.(20+5)=785.398
𝑐𝑚2
785.398 .10= 7853.98 𝑐𝑚2

6. Volumen del cilindro
 El volumen es
el espacio que ocupa
un cuerpo.
 V=n.𝑟2.h