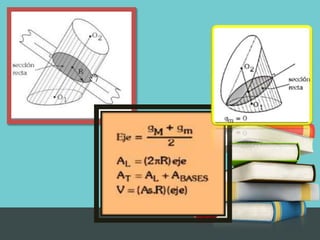
El documento describe la evolución del artista Javier Carvajal de usar el plano como objeto de investigación estética a enfocarse en el cilindro. Explica que ha creado formas complejas guiado por la lógica de los movimientos y la búsqueda de la belleza. Luego presenta algunas definiciones matemáticas y propiedades geométricas del cilindro y el tronco de cilindro, incluyendo fórmulas para calcular su volumen, área y variaciones respecto al radio y la altura.

2. Hace algunos años que Javier Carvajal dejó el plano, el
inagotable plano, como objeto directo de su
investigación estética. Hace menos tiempo
que, trabajando con figuras poliédricas de aristas
cilíndricas, quedó atrapado, hipnotizado, por las
posibilidades de ese cuerpo redondo y, a la vez, recto:
el cilindro. Desde la simplicidad de este cuerpo ha
creado formas complejas, guiado por dos fuerzas
evolutivas: la lógica de los movimientos y la búsqueda
de la belleza.

3. Es el sólido que se genera mediante una rotación
de 360° de una región rectangular alrededor de
uno de sus lados.
Back to
school

5. Consideramos un cilindro de revolución , el
cual es intersecado por un plano no paralelo a
sus bases, denominado sección plana , que
divide el cilindro en dos sólidos . A cada uno de
estos sólidos se le denomina Tronco de cilindro.

6. El tronco de cilindro de revolución es el sólido
que se obtiene al cortar el cilindro de
revolución por un plano no paralelo a sus
bases.

7. Base inferior
Base superior
Eje del tronco
generatriz menor
generatriz mayor
radio

8. Dado el tronco de cilindro de la figura:
Al desarrollar su superficie lateral obtenemos, dos
regiones trapezoidales congruentes:
Luego al calcular el área de la región ABCDE
obtenemos el área lateral del tronco de cilindro
Back to
recto. Así: school

9. AT=AL+AB+AB1

10. Para calcular el volumen del tronco de cilindro recto de
generatrices Gy g , y de base circular con radio r, se
aplica la siguiente fórmula:

13. A continuación trataremos las variaciones que se
producen en el volumen y el perímetro de la
circunferencia al incrementar o disminuir el radio o
la altura en un cilindro
Variación del Volumen en función del radio y la altura:

16. Variación del Perímetro de una circunferencia en función
del radio:
Back to
school

17. Back to
school

18. Variación del área de un círculo en función de su radio: