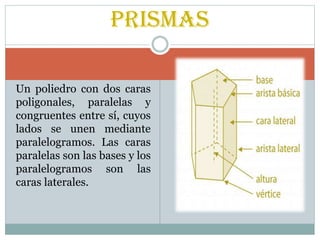
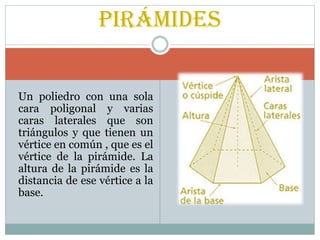
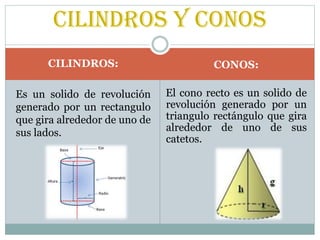
Este documento presenta fórmulas para calcular áreas y volúmenes de diferentes poliedros como prismas, pirámides, cilindros y conos. Explica que un prisma es recto cuando sus aristas laterales son perpendiculares a las bases, y proporciona fórmulas para calcular su área lateral, área total y volumen. También define una pirámide como un poliedro con una sola cara poligonal y varias caras laterales triangulares compartiendo un vértice común, y ofrece fórmulas similares

1. P R E S E N T A C I Ó N : Z O I L A G E R A L D I N E P A R E D E S A L Q U I Z A R
Los poliedros

2. Un poliedro con dos caras
poligonales, paralelas y
congruentes entre sí, cuyos
lados se unen mediante
paralelogramos. Las caras
paralelas son las bases y los
paralelogramos son las
caras laterales.
Prismas

3. Áreas y volumen de un prisma recto
Un prisma es recto
cuando las aristas
laterales son
perpendiculares a las
bases. Su desarrollo plano
está compuesto por un
rectángulo y dos
polígonos congruentes
que son las bases.
Área lateral Área total Volumen
AL= Pb x h AT= AL+2.Ab V=Ab x h

4. Un poliedro con una sola
cara poligonal y varias
caras laterales que son
triángulos y que tienen un
vértice en común , que es el
vértice de la pirámide. La
altura de la pirámide es la
distancia de ese vértice a la
base.
Pirámides

5. Áreas y volumen de una pirámide recta
Una pirámide es recta
cuando sus caras
laterales están formadas
por triángulos isósceles.
Su desarrollo plano esta
compuesto por el
polígono de la base y
tantos triángulos isósceles
como lados tenga la base.
Área lateral Área total Volumen
AL= (Pb x Ap)/2 AT= AL + Ab V=(Ab x h)/3

6. Áreas y volumen de un Troco de pirámide
Si se corta una pirámide
recta por un plano paralelo a
la base, se obtiene un tronco
de pirámide. Su desarrollo
plano está compuesto por
dos polígonos semejantes y
tantos trapecios congruentes
como lados tenga la base.
Área lateral Área total Volumen
AL= [n(l’ + l)]/2 x Ap’ AT= AL + Ab1 + Ab2 V=h/3(Ab1 + Ab2 +¬/Ab1 x Ab2)

7. CILINDROS:
Es un solido de revolución
generado por un rectangulo
que gira alrededor de uno de
sus lados.
CONOS:
El cono recto es un solido de
revolución generado por un
triangulo rectángulo que gira
alrededor de uno de sus
catetos.
Cilindros y conos

8. Áreas y volumen de un cilindro recto
El desarrollo de un cilindro
es un rectangulo y dos
círculos. El rectangulo tiene
por base la longitud de la
circunferencia (2π.r) y por
altura la generatriz (h=p).
Las bases del cilindro son
dos círculos congruentes y su
área lateral es igual al área
del rectangulo.
Área lateral Área total Volumen
AL= 2πr.g AT= 2πr(g + r) V=πr2 . h

9. Áreas y volumen de un cono recto
El desarrollo de un cono esta
formado por un sector circular
y un circulo.
El arco del sector circular tiene
de longitud 2π.r ( siendo r el
radio del cono(, ya que es la
longitud de la circunferencia de
la base.
El radio del sector circular es la
generatriz (g).
Área lateral Área total Volumen
AL= πr.g AT= πr(g + r) V=[πr2 . H]/3

10. Áreas y volumen de un Troco de cono
Es la porción de cono
comprendida entre la base y la
sección transversal determinada
por un plano paralelo a la base.
El desarrollo de un tronco de
cono esta formado por un
trapecio circular y dos círculos de
radio r y R.
El trapecio circular tiene por
bases las longitudes de ambas
circunferencias (2 πR y 2 πr).
Área lateral Área total Volumen
AL=[2πR + 2πr]/2 x g AT=πg(r + R) + πr2 + πR2 V=[πh’(r2 + R2 + r.R)]/3

11. **Gracias**