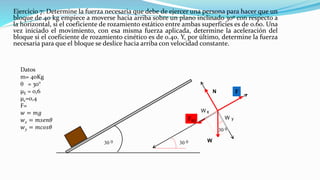
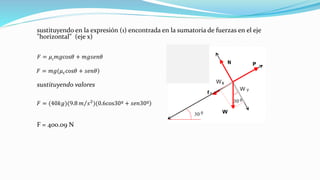
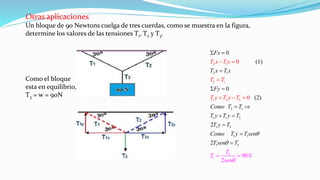
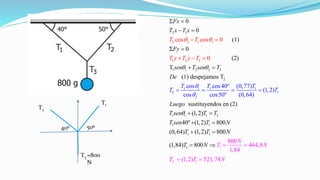
Este documento introduce los conceptos fundamentales de la dinámica, incluyendo la masa, peso, fuerza, y las tres leyes de Newton. Explica que la dinámica estudia las relaciones entre movimiento y fuerzas, y que Galileo y Newton sentaron las bases de la mecánica clásica al introducir el método científico y formular las leyes del movimiento respectivamente. También presenta ejemplos para ilustrar cómo aplicar las leyes de Newton para resolver problemas de dinámica.

1. DINÁMICA

2. Introducción
▪ La Dinámica estudia las relaciones entre los movimientos de
los cuerpos y las causas que los provocan.
▪ Para entender estos fenómenos, el punto de partida es la
observación del mundo cotidiano. Si se desea cambiar la
posición de un cuerpo en reposo es necesario empujarlo o
levantarlo, es decir, ejercer una acción sobre él.

3. ▪ Un avance muy importante se debió a Galileo (1564-1642)
quien introdujo el método científico, que enseña que no
siempre se debe creer en las conclusiones intuitivas basadas
en la observación inmediata, pues esto lleva a menudo a
equivocaciones.
▪ Galileo en concreto, observo como un cuerpo quo se mueve
con velocidad constante sobre una superficie lisa se moverá
eternamente si no hay rozamientos ni otras acciones externas
sobre él.

4. ▪ Esta relación entre fuerza y cambio de velocidad (aceleración) constituye
la base fundamental de la Mecánica Clásica. Fue Isaac Newton (hacia
1690) el primero en dar una formulación completa de las leyes de la
Mecánica. Y además invento los procedimientos matemáticos necesarios
para explicarlos y obtener información a partir de ellos.
▪ Antes de enunciar las leyes introduciremos con precisión los conceptos
de Masa, Peso y Fuerza, que son básicos en ellas:
▪ Masa.
▪ Es el parámetro característico de cada objeto que mide su resistencia a
cambiar su velocidad. Es una magnitud escalar y aditiva.

5. Peso
El peso es una fuerza gravitacional ejercida por la aceleración de
la Tierra (u otro planeta). El peso depende de la gravedad, la que
depende de la distancia a la que se encuentre el cuerpo respecto
de la Tierra. Para distancias cercanas a la Tierra, la gravedad es
igual a 9,8 m/s2.
𝑃 = 𝑚𝑔
El peso es una fuerza y por la segunda ley de Newton se
calcula como masa por la aceleración de la gravedad.

6. Diferencia entre la masa y el peso
El peso de un objeto es
igual a la magnitud de
la fuerza gravitacional
ejercida sobre el objeto
y varia con la posición
La masa es una propiedad
inherente de un objeto y es
independiente de los
alrededores del objeto y del
método que se aplica para
medirla

7. Fuerza.
Todos tenemos un concepto intuitivo de que es una fuerza.
Aunque dar una definición rigurosa y precisa no es sencillo, sí que
tiene unas propiedades básicas observables en la vida cotidiana:
1. Es una magnitud vectorial.
2. Las fuerzas tienen lugar en parejas.
3. Una fuerza actuando sobre un objeto hace que este o bien
cambie su velocidad o bien se deforme.
4. Las fuerzas obedecen el Principio de superposición: varias
fuerzas concurrentes en un punto dan como resultado otra fuerza
que es la suma vectorial de las anteriores.
Dinamómetro

8. Leyes de Newton:
1. Primera ley (Principio de inercia): Todo cuerpo permanece en su estado inicial
de reposo o movimiento restímelo uniforme a menos que sobre él actué una
fuerza externa neta no nula.
2. Segunda ley: La aceleración de un objeto es inversamente proporcional a su
masa y directamente proporcional a la fuerza neta que actúa sobre él
donde F es la suma vectorial de todas las fuerzas que actúa sobre el (fuerza
neta).
3. Tercera ley (Principio de Acción-Reacción) : Si un objeto A ejerce una fuerza
sobre un objeto B, este ejerce sobre el A una fuerza igual en modulo y dirección,
pero de sentido contrario.

9. La primera Ley de Newton no distingue entre
un cuerpo en reposo y otro en movimiento
rectilíneo uniforme. Esto sólo depende del
sistema de referencia desde el que se observa
el objeto.
Ejemplo un vagón en el que se coloca una
mesa con un libro sobre su superficie, de
manera que no existe fricción entre el libro y
la mesa. Si el vagón se mueve con velocidad
uniforme v = cte. y sobre el libro no actúa
fuerza alguna, seguirá en reposo sobre la
mesa, tanto para un observador sobre el vagón
(O) como para un observador sobre la vía (O').
Primera ley de newton

10. En este caso el libro permanecerá en reposo
respecto a la vía, pero no respecto al vagón. Y
sobre él no actúa ninguna fuerza Esto quiere
decir que la primera ley de Newton no se
verifica en cualquier sistema de referencia.
Sin embargo, supongamos que inicialmente el
vagón esta en reposo y que en el instante t = 0
comienza a avanzar con una cierta
aceleración, a.

11. Por tanto, se denominan sistemas de referencia inerciales a aquellos en
los que si se verifica la ley de la inercia: Un sistema de referencia inercial
es aquel en que un cuerpo que no esta sometido a la acción de ninguna
fuerza se mueve con velocidad constante.
Sistemas de Referencias Inerciales

12. Fuerza, masa y segunda Ley de Newton
• La primera ley de Newton explica que le sucede a un objeto cuando la
resultante de todas las fuerzas externas sobre él es nula.
• La segunda explica lo que le sucede cuando se ejerce una fuerza neta no nula
sobre él.
Una fuerza es la causa capaz de provocar en un cuerpo un cambio de velocidad,
es decir, una aceleración. Además. la dirección de la aceleración coincide con la
de la fuerza y el parámetro que relaciona fuerza y aceleración es precisamente la
masa del objeto, una propiedad intrínseca a él.
Unidades y dimensiones de la fuerza:
Unidades S.I.: newton = kg.m/s2.
Sistema cegesimal: 1 N= 105 dinas.
𝐹 = 𝑚
𝑑𝑣
𝑑𝑡
= 𝑚𝑎
𝐹 =
𝑑(𝑚𝑣)
𝑑𝑡

13. ¿CÓMO SE APLICA LA SEGUNDA LEY DE NEWTON?
• PASO 1. Diagrama de Cuerpo Libre. Constatación del movimiento acelerado.
• PASO 2. Se trasladan las fuerzas al plano cartesiano y se descomponen.
• PASO 3. Se aplica la segunda ley de Newton.
A
A

B

14. Ejercicio 1.
Con una fuerza F a 20° con respecto de la horizontal se jala un cuerpo de 4,7 kg sobre una
superficie horizontal, con una aceleración de 2,0 m/s2. ¿Cual es el valor de la magnitud de
la fuerza?
Datos y
reducciones
Formulas Sustitución Resultados
𝜃 = 20°
𝑚 = 4,7𝑘𝑔
𝑎 = 2.0 𝑚/𝑠2
𝐹 =? (New)
σ 𝐹𝑥 = 𝑚𝑎 𝑥
𝐹𝑐𝑜𝑠𝜃 = 𝑚𝑎 𝑥
𝐹 =
𝑚𝑎 𝑥
𝑐𝑜𝑠𝜃
𝐹 =
(4,7)(2)
𝑐𝑜𝑠20°
𝐹 = 8,84𝑁
20°
F
x

15. Ejercicio 2 .
Una fuerza constante actúa sobre un cuerpo de 100 kg y en 5 s cambia su velocidad
de 10 m/s a 15 m/s. ¿Cual es la magnitud de esa fuerza?
Datos y
reducciones
Formulas Sustitución Resultados
𝑚 = 100 𝑘𝑔
𝑡 = 5 𝑠𝑒𝑔
𝑣0 = 10 𝑚/𝑠
𝑣 = 15 𝑚/𝑠
𝐹 =? (New)
𝐹 = 𝑚𝑎 ,
𝑣 = 𝑣0 + 𝑎𝑡 𝑎 =
𝑣−𝑣0
𝑡
𝐹 =
𝑚(𝑣 − 𝑣0)
𝑡
𝐹 =
100(15 − 10)
5
𝐹 = 100𝑁

16. Ejercicio 3
Sobre un bloque, de 15 kg de masa, actúa una fuerza F de valor igual a 35
newtons. Determine la aceleración (No considere efectos de rozamiento)
Datos y
reducciones
Formulas Sustitución Resultados
𝑚 = 15 𝑘𝑔
F = 35 N
𝑎 =?
σ 𝐹𝑥 = 𝑚𝑎 𝑥
𝐹𝑐𝑜𝑠𝜃 = 𝑚𝑎 𝑥
𝑎 𝑥 =
𝐹𝑐𝑜𝑠𝜃
𝑚
𝑎 𝑥 =
35cos37°
15
𝑎 𝑥 = 1,86𝑚/𝑠2

17. Ejercicio 4.
Un cuerpo de masa m = 3 kg ejecuta un movimiento rectilíneo a lo largo del
eje x; de acuerdo con la ley de movimiento, x = 3+5t + 8t2 (m). Bajo estas
condiciones, cuál es la magnitud de la fuerza resultante?
Datos y
reducciones
Formulas Sustitución Resultados
𝑚 = 3 𝑘𝑔
𝑥 = 3 + 5𝑡 + 8𝑡2
𝑡 = 5𝑠
𝐹 =? (New)
𝑣 =
𝑑𝑥
𝑑𝑡
= 5 + 16𝑡
𝑎 =
𝑑𝑣
𝑑𝑡
=16
𝐹 = 𝑚𝑎
𝐹 = 3 ∗ 16 𝐹 = 48𝑁

18. Tercera ley de acción y reacción
Esta ley dice que, si un cuerpo A ejerce una acción sobre otro B, este reacciona sobre el
primero con una reacción igual y de sentido contrario. Ambas cosas ocurren
simultáneamente y siempre las dos fuerzas actúan sobre distintos objetos.
w
෍ 𝐹𝑥 = 𝑁 − 𝑤 = 0
𝑁 = 𝑤
𝑤 = 𝑚𝑔
N= 𝑚𝑔

19. Aplicaciones de las Leyes de Newton
Para resolver problemas aplicando las leyes de Newton, se recomienda:
 Hacer el diagrama de cuerpo libre o aislado, considerando al cuerpo
como si fuese un punto.
 Colocar en el diagrama y saliendo del punto, todas las fuerzas que actúan
sobre el cuerpo.
 Elegir un sistema de referencia (plano cartesiano)
 Colocar en el sistema la convención de signos.
 Tomar como eje positivo el de la dirección de movimiento del cuerpo.
 Marcar los ángulos que forman las fuerzas con respecto a los ejes.
 Descomponer a las fuerzas en sus componentes rectangulares.
 Cuando se trabaje con planos inclinados, uno de los ejes debe de ser
paralelo al plano.
 Aplicar la Segunda Ley de Newton, haciendo la sumatoria de las
componentes de las fuerzas sobre los ejes.
xx maF = yy maF =

20. Ejercicio 5
Una persona empuja una caja de 50 kg sobre una superficie horizontal lisa
aplicando una fuerza de 30 N. Determine la aceleración de la caja.
La única fuerza que está actuando sobre el eje de las x es la Fuerza F aplicada,
además, tal fuerza es igual a la componente Fx , por lo tanto:
Solución:
despejando a la aceleración:
Diagrama de Cuerpo libre
N
F
w
x+
y+
xx maF =
2
6.0
50
30
s
m
kg
N
m
F
a ===
Datos
m=50Kg
F=30N
F ma=

21. En este tipo de problemas donde no existe fricción, no es necesario realizar la
suma de fuerzas en el eje de las Y a menos que se solicite.
Las fuerzas que actúan sobre el eje de las Y son la Normal (positiva hacia arriba)
y el peso (negativo hacia abajo).
Como no hay movimiento en dicho eje, la aceleración aquí es cero (no hay
cambios de velocidad). Por lo tanto:
ya que el peso es igual a la masa por la aceleración de la gravedad (w = mg).
yy maF =
ymawN =−
0=− wN
N
s
m
kgmgwN 5.490)81.9(50 2
====

22. Ejercicio 5 (continuación).- Del ejemplo anterior, la persona le aplica a la caja la
misma fuerza, pero haciendo un ángulo de 20º con respecto a la horizontal.
Determine la aceleración que tal fuerza le produce a la caja.
donde las componentes rectangulares de F se determinan a partir del triángulo
que se forma:
Aplicando la suma de fuerzas en x:
Diagrama de Cuerpo libre
N
F
w
x+
y+
200
Fx
-Fy
NNNFx 19.28)9396.0(30)20(cos30cos 0
==== F
NNsenNsenFy 26.10)342.0(30)20(30 0
==== F

23. xx maF =
F ma=
2
28.19
0.5638
50
F N m
a
m kg s
= = =
Como se puede observar de los dos resultados, la aceleración máxima se
obtiene cuando la fuerza aplicada es horizontal. A medida que aumentamos
el ángulo de aplicación de la fuerza, la aceleración disminuye.

24. Ejercicio 5. : Del mismo problema, pero cuando la caja es subida por un
plano inclinado 200 con respecto a la horizontal.
Diagrama de Cuerpo libre
N F
W
x+
y+
200
200
wy
wx

25. Suma de fuerzas en x Suma de fuerzas en y
xx maF =
xx mawF =−
xmasenmgF =− 
m
mgsenF
ax
−
=
kg
sen
s
m
kgN
ax
50
20)81.9(5030 0
2
−
=
kg
nN
ax
50
76.16730 −
=
kg
N
ax
50
76.137−
=
2
75.2
s
m
ax −=
ymaFy =
).( ejeesteenmovhaynomawN yy =−
0cos =− mgN
cosmgN =
0
2
20cos)819(50
s
m
kgN −=
NN 919.460=

26. Dinámica Segunda Parte (Fricción)
INTRODUCCIÓN
Una de las principales fuerzas que existen en la naturaleza son las fuerzas de
fricción o de rozamiento.
La fuerza de fricción o de rozamiento es aquella fuerza que se opone al
movimiento entre dos superficies que están en contacto
Esta fuerza se debe a las imperfecciones que existen en ambas superficies.

27. Imagina que tienes que mover un mueble pesado en tu casa, por ejemplo, el
refrigerador. Para moverlo hay que aplicar una fuerza sobre él. Supón que lo haces.
Verás que el refrigerador no se mueve nada en lo absoluto.
Al no moverse significa que sigue en su sitio, es decir, está estático.
Pues es justamente en ese momento en que, a pesar de que se ejerció una pequeña
fuerza sobre él no se movió, está haciendo efecto el rozamiento estático.
Posteriormente, al vencer esa fuerza que impide que el refrigerador se mueva, se
hace fácil trasladarlo.
Ya en movimiento, en el refrigerador (haciéndolo lenta y uniformemente) estará
actuando el rozamiento cinético.

28. La fuerza de rozamiento depende de dos factores:
• La fuerza normal (N), es decir, el peso del cuerpo sobre la superficie.
• Los materiales de los cuerpos que están en contacto haciendo
rozamiento.
La fuerza de rozamiento, tanto cinética como estática, se expresa en
función de la normal (N), de la siguiente forma:
• 𝐹 𝑅𝐸 = 𝜇 𝐸 𝑁
• 𝐹 𝑅𝐶 = 𝜇 𝐶 𝑁
En donde µE representa el coeficiente de rozamiento estático y µC
representa el coeficiente de rozamiento cinético y ambos dependen del
material de que están hechas las superficies que están en contacto.

29. Tabla de coeficientes de rozamiento
Materiales en
contacto
Coeficiente roce
estático
Coeficiente roce
cinético
Hielo / Hielo 0.1 0.03
Vidrio / Vidrio 0.9 0.4
Madera / Cuero 0.4 0.3
Madera / Piedra 0.7 0.3
Madera / Madera 0.4 0.3
Acero / Acero 0.74 0.57
Caucho / Cemento 1.0 0.8

30. Supónganos que tenemos que mover una silla de madera sobre el piso de
madera. La masa de la silla es de 10 kg.
a) Determina la fuerza necesaria para sacarla del estado de reposo.
b) Determina la fuerza necesaria para mantenerla en movimiento constante.
Considera g = 9.8 m/s2
Ejercicio 6
Datos y
reducciones
Formulas Sustitución Resultados
𝑚 = 10𝐾𝑘
𝑔 = 9,8𝑚/𝑠2
E =0,4
C =0,3
𝐹 𝑅𝐸=
𝐹 𝑅𝐶 =
𝑁 = 𝑤 = 𝑚𝑔
𝐹 𝑅𝐸 =  𝐸 𝑁
𝐹 𝑅𝐶 =  𝐶 𝑁
𝑁 = 10 ∗ 9,8
𝐹 𝑅𝐸 = 0,4 ∗ 98
𝐹 𝑅𝐶 = 0,3 ∗ 98
𝐹 = 98𝑁
𝐹 𝑅𝐸 = 39,2𝑁
𝐹 𝑅𝐶 = 29,4𝑁
Entonces, FRE es la fuerza necesaria para mover la silla desde su estado de reposo.
Y, FRC es la fuerza necesaria para que la silla se mantenga en movimiento sobre el
piso.

31. Ejercicio 7: Determine la fuerza necesaria que debe de ejercer una persona para hacer que un
bloque de 40 kg empiece a moverse hacia arriba sobre un plano inclinado 30º con respecto a
la horizontal, si el coeficiente de rozamiento estático entre ambas superficies es de 0.60. Una
vez iniciado el movimiento, con esa misma fuerza aplicada, determine la aceleración del
bloque si el coeficiente de rozamiento cinético es de 0.40. Y, por último, determine la fuerza
necesaria para que el bloque se deslice hacia arriba con velocidad constante.
 
N
W
W x
W y
P
f s
 
 
F
FRE
Datos
m= 40Kg
 = 30°
μE = 0,6
μc=0,4
F=
𝑤 = 𝑚𝑔
𝑤 𝑥 = 𝑚𝑠𝑒𝑛𝜃
𝑤 𝑦 = 𝑚𝑐𝑜𝑠𝜃

32. Para que empiece a moverse:
De la aplicación de la segunda ley al diagrama de cuerpo libre
tenemos que:
σ 𝐹 𝑥 = 𝑚𝑎𝑥
𝐹 − 𝐹𝑅𝐸 − 𝑤𝑥 = 0 (1) (el cuerpo está en reposo, ax = 0 )
𝐹 = 𝐹𝑅𝐸 + 𝑤𝑥
𝐹 = 𝜇 𝑅𝐸 𝑁 + 𝑚𝑔𝑠𝑒𝑛𝜃 (2)
De la suma de fuerzas en el eje vertical, determinamos a la fuerza normal.
෍ 𝐹 𝑦 = 𝑚𝑎𝑦
𝑁 − 𝑤𝑦 = 0 (3)
(el cuerpo en ningún momento se mueve en el eje vertical, ay= 0 )
𝑁 = 𝑚𝑔𝑐𝑜𝑠𝜃 (4)
FR
E

33. sustituyendo en la expresión (1) encontrada en la sumatoria de fuerzas en el eje
"horizontal" (eje x)
sustituyendo valores
F = 400.09 N
𝐹 = 𝜇 𝑐 𝑚𝑔cos𝜃 + 𝑚𝑔𝑠𝑒𝑛𝜃
)𝐹 = 𝑚𝑔(𝜇 𝑐cos𝜃 + 𝑠𝑒𝑛𝜃
)𝐹 = (40𝑘𝑔)(9.8 Τ𝑚 𝑠2)(0.6cos30º + 𝑠𝑒𝑛30º

34. El cuerpo ya se está moviendo y el coeficiente pasa a ser uno de
rozamiento cinético, con esa misma fuerza aplicada de 400.09 N el
cuerpo se acelera, la aceleración es:
𝐹𝑥 = 𝑚𝑎 𝑥
𝐹−𝐹 𝑅𝐶−𝑤 𝑥=𝑚𝑎 𝑥
m
wFF
a xRC −−
=
m
mgsenNF
a C  −−
= (5)

35. De la suma de fuerzas en el eje vertical, determinamos a la fuerza normal.
Ecuaciones (3 y 4)
෍ 𝐹 𝑦 = 𝑚𝑎𝑥
𝑁 − 𝑤𝑦 = 0 (3)
(el cuerpo en ningún momento se mueve en el eje vertical ay= 0 )
𝑁 = 𝑚𝑔𝑐𝑜𝑠𝜃 (4)
Sustituyendo (4) en la expresión (5) de la aceleración encontrada en la sumatoria
de fuerzas en el eje "horizontal" (eje x)
sustituyendo valores
a = 1.69 m/s2
m
mgsenmgF
a C  −−
=
cos
m
mgsenNF
a C  −−
=

36. Ahora determinaremos la fuerza necesaria para que el cuerpo se siga moviendo
hacia arriba con velocidad constante
෍ 𝐹 𝑥 = 𝑚𝑎𝑥
𝐹 − 𝐹𝑅𝐶 − 𝑤𝑥 = 0
(el cuerpo está moviéndose con velocidad constante, ax = 0 )
𝐹 = 𝐹𝑅𝐶 + 𝑤𝑥 = 0
𝐹 = 𝜇 𝑐 𝑁 + 𝑚𝑔𝑠𝑒𝑛𝜃
De la suma de fuerzas en el eje vertical, determinamos a
la fuerza normal.
෍ 𝐹 𝑦 = 𝑚𝑎𝑦
𝑁 − 𝑤𝑦 = 0

37. (el cuerpo en ningún momento se mueve en el eje vertical ay = 0 )
𝑁 = 𝑚𝑔𝑐𝑜𝑠𝜃
sustituyendo en la expresión de F encontrada en la sumatoria de fuerzas en el eje
"horizontal" (eje x)
𝐹 = 𝜇 𝑐 𝑁 + 𝑚𝑔𝑠𝑒𝑛𝜃
𝐹 = 𝜇 𝑐 𝑚𝑔𝑐𝑜𝑠𝜃 + 𝑚𝑔𝑠𝑒𝑛𝜃
𝐹 = 𝑚𝑔(𝜇 𝑐 𝑐𝑜𝑠𝜃 + 𝑠𝑒𝑛𝜃)
sustituyendo valores
F = ( 40 kg )( 9.81m/s2 )( 0.4 cos 300 + sen 300 )
F = 332.13 N.

38. Otras aplicaciones
Un bloque de 90 Newtons cuelga de tres cuerdas, como se muestra en la figura,
determine los valores de las tensiones T1, T2 y T3.
Como el bloque
esta en equilibrio,
T3 = w = 90N
2 1
2
2 1
2 1
1 1 3
1 3
1
1
1 2
1
1 3
3
1
3
0
(1)
0
(2)
2
2
0
0
2
9
0
Fx
T x T x
Fy
Como T T
T y T y T
T y T
Como T
T
T
T x T x
y T sen
T sen T
T T
T y T
sen
y T
N



− =
=
+ − =
 =
=
 =
= 
+ =
=
=
=
=
=

39. 2 1
1 1
2 2 1 1
2 2 3
1 1 1 1
2 1
2
1
2
1 2 3
0
0
(1)
Σ 0
(2)
T
(1)
cos cos40º (0,77)
(1,2)
cos cos50º (0,
despejamos T
sustituyendo
cos cos
s e
64
n
0
)
0
(2)
T T
Fx
T x T x
Fy
sen T sen T
De
Lueg
T T
T y T y T
T
T T
o
T sen
 
 



 =
− =
+ − =
= =
=
=
+
= =
−
=
1 1
1
3
1 1
1 1
1
2 1
(1,2)
40º (1,2) 800
(0,64) (1,2) 800
800
(1,84 464,8
1,84
(1,2) 521,7
) 800
4
N
T T
T sen T N
T T N
T N T N
T T N
+ =
+ =
+ =
 =
=
= =
=
50º40º
=800
N
T1
T2
T3

40. Un bloque que cuelga, de 8.5 kg. se conecta por medio de una cuerda que pasa por una polea a un bloque
de 6.2 kg que se desliza sobre una mesa plana (figura ). Si el coeficiente de fricción durante el
deslizamiento es 0.20, encuentre la tensión en la cuerda.
6,2 Kg
8,5 Kg
y Luego
(1)
(2)
(1) y (2)
(
A
( )
)
B
A
A
A A
B
B
A A
B B
B A
A
B A
A
B B
A
B
B
A
Fx m a
T fc m a
Pero fc N N m g fc m g
Fy m a
w T m a
Sumando
T m g m
T m g m a
m g T
a
m g T m a
m g m g m m
m a
Bloque
m g m g
a
m m
Bloque
a






 =
− =
= =  =
 =
− =
− =
− =
− = + 
−
=
=
+
− =
−
2
4,83 /
(2) calculamos la tensión: 42,2B B
m s
De m m Ng T Ta =
=
− = 
Datos
mA=6,2 Kg
mB=8,5 Kg
 = 0,2
Fc = fuerza de fricción
w=mg
N = w = mg
g = 9,8 m/s2

41. LEY DE HOOKE
La ley de Hooke describe fenómenos elásticos como los que exhiben los resortes helicoidales.
Esta ley afirma que la deformación elástica que sufre un cuerpo es proporcional a la fuerza que
produce tal deformación, siempre y cuando no se sobrepase el límite de elasticidad.
La fórmula más común de la ley de Hooke es:
F = -k . Δx
Donde:
•F es la fuerza deformante
•Δx es la variación que experimenta la longitud del resorte,
ya sea una compresión o extensión.
•k es la constante de proporcionalidad o de restitución del
resorte, generalmente expresada en Newtons sobre metros
(N/m).

42. Ejercicio 8: Una masa de 4 kg suspendida de un resorte produce un
desplazamiento de 20 cm. ¿Cuál es la constante de resorte?
F20 cm
m
La fuerza que estira es el peso (W = mg) de la masa de 4
kg:
Ahora, a partir de la ley de Hooke, la constante de fuerza k del resorte es:
𝐾 = −
𝐹
∆𝑥
=
39,92
0,2
= 196𝑁/𝑚
𝐹 = −𝐾∆𝑥
𝐷𝐴𝑇𝑂𝑆
W=4kg = 4kg*9,8m/s2 = 96,2N
∆𝑥 = 20𝑐𝑚 = 0,2𝑚
𝑆𝑂𝐿𝑈𝐶𝐼Ó𝑁

43. Ejercicio 9.- Una carga de 50 N unida a un resorte que cuelga verticalmente estira el
resorte 5 cm. El resorte se coloca ahora horizontalmente sobre una mesa y se estira
11 cm. a) ¿Qué fuerza se requiere para estirar el resorte esta cantidad?
𝐷𝐴𝑇𝑂𝑆
W = 50N
𝑥 = 5𝑐𝑚 = 0,05𝑚
F = ?
∆𝑥 = 11𝑐𝑚 = 0,11𝑚
Para calcular la constante K utilizamos el
peso W ya que esta en Newtons
𝑆𝑂𝐿𝑈𝐶𝐼Ó𝑁
𝑘 =
50𝑁
0,05𝑚
= 1000N7m
Luego
𝐹 = 𝐾∆𝑥 =
1000𝑁
𝑚
∗ 0,11𝑚 = 110𝑁

44. Ejercicio. 10 Se cuelga de un muelle una bola de masa de 15 kg, cuya constante elástica
vale 2100 N/m, determinar el alargamiento del muelle en centímetros.
DATOS
m=15kg
K=21 N/m
K=2100N/m
SOLUCIÓN
Si tenemos la masa, podemos calcular el peso que finalmente viene siendo nuestra fuerza
ejercida
𝑤 = 𝑚. 𝑔 = (15𝑘𝑔)(
9,8𝑚
𝑠2
) = 147𝑁
𝑥 =
𝐹
𝐾
=
147𝑁
2100𝑁/𝑚
= 0,07𝑚 = 7𝑐𝑚