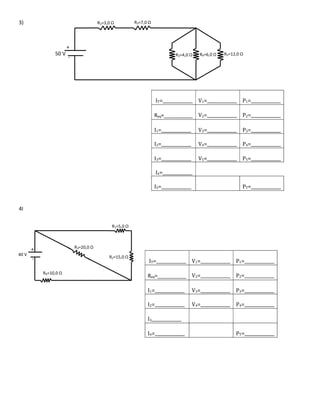
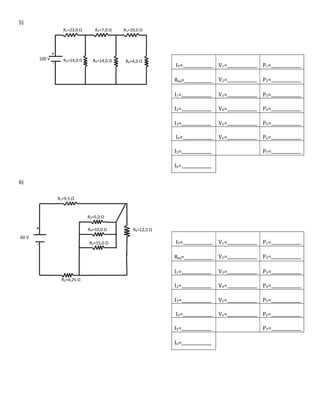
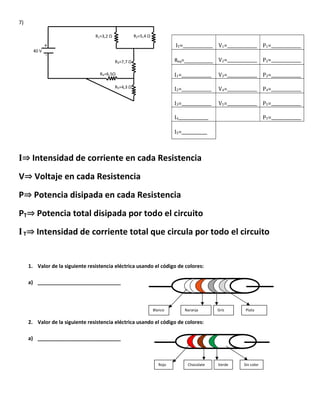
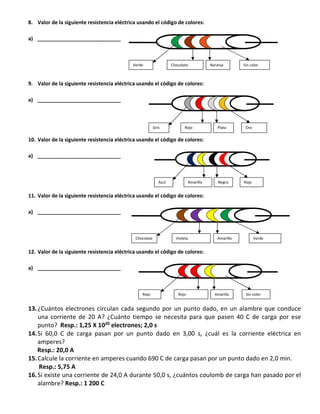
El documento trata sobre electrocinética. Explica que estudia las cargas eléctricas en movimiento y los fenómenos eléctricos como la corriente eléctrica y los circuitos eléctricos. Define conceptos clave como la intensidad de corriente, corriente alterna, corriente directa, resistencia eléctrica y ley de Ohm.