Este documento presenta nociones generales sobre funciones. Define una función como una relación entre dos cantidades donde una depende de la otra. Explica conceptos básicos como variable, dominio, codominio, gráfico e intervalos de monotonía. Describe diferentes tipos de funciones como lineales, cuadráticas y radicales. Finalmente, cubre temas como operaciones con funciones, funciones inversas y composición de funciones.

1. 1 Nociones generales sobre funciones
1.1 Introducci´on
Una funci´on, en matem´aticas, es el t´ermino usado para indicar la relaci´on o correspondencia entre dos o m´as cantidades.
El t´ermino funci´on fue usado por primera vez en 1637 por el matem´atico franc´es Ren´e Descartes1 para designar una
potencia xn de la variable x.
En 1694 el matem´atico alem´an Gottfried Wilhelm Leibniz2 utiliz´o el t´ermino para referirse a varios aspectos de una curva,
como su pendiente. Hasta recientemente, su uso m´as generalizado ha sido el definido en 1829 por el matem´atico alem´an,
Lejeune-Dirichlet3, quien escribi´o: una variable es un s´ımbolo que representa un n´umero dentro de un conjunto de ellos.
Muchas cantidades dependen de otras, por ejemplo:
• Los costos totales de producci´on, C, depende de la cantidad q de art´ıculos a producir.
• El nivel de contaminaci´on en una determinada regi´on puede depender del n´umero de veh´ıculos circulando en la v´ıa.
• El ´area de un c´ırculo depende del radio.
• La presi´on depende de la temperatura.
Para describir como una cantidad depende o es determinada por otra se usa el concepto de funci´on.
El estudio de las propiedades de las funciones est´a presente en todo tipo de fen´omenos que acontecen a nuestro alrededor.
As´ı, podemos nombrar fen´omenos sociales relacionados con crecimientos demogr´aficos, con aspectos econ´omicos, como
la inflaci´on o la evoluci´on de los valores burs´atiles, con todo tipo de fen´omenos f´ısicos, qu´ımicos o naturales, como la
variaci´on de la presi´on atmosf´erica, la velocidad y la aceleraci´on, la gravitaci´on universal, las leyes del movimiento,
la funci´on de onda de una part´ıcula a escala cu´antica, la desintegraci´on de sustancias radiactivas o la reproducci´on de
1Ren´e Descartes (La Haye, Turena francesa, 31 de marzo de 1596 - Estocolmo, Suecia, 11 de febrero de 1650), tambi´en llamado Renatus Cartesius,
fue un fil´osofo, matem´atico y f´ısico franc´es, considerado como el padre de la geometr´ıa anal´ıtica y de la filosof´ıa moderna, as´ı como uno de los nombres
m´as destacados de la revoluci´on cient´ıfica.
2Gottfried Wilhelm Leibniz, a veces von Leibniz (Leipzig, 1 de julio de 1646 - Hannover, 14 de noviembre de 1716) fue un fil´osofo, l´ogico,
matem´atico, jurista, bibliotecario y pol´ıtico alem´an. Fue uno de los grandes pensadores de los siglos XVII y XVIII, y se le reconoce como el ´ultimo
genio universal. Realiz´o profundas e importantes contribuciones en las ´areas de metaf´ısica, epistemolog´ıa, l´ogica, filosof´ıa de la religi´on, as´ı como a la
matem´atica, f´ısica, geolog´ıa, jurisprudencia e historia.
3Johann Peter Gustav Lejeune Dirichlet (D¨uren, actual Alemania, 13 de febrero de 1805 - G¨ottingen, actual Alemania, 5 de mayo de 1859) fue un
matem´atico alem´an al que se le atribuye la definici´on formal moderna de una funci´on. Fue educado en Alemania, y despu´es en Francia, donde aprendi´o
de muchos de los m´as renombrados matem´aticos del tiempo, relacion´andose con algunos como Fourier. Sus m´etodos proporcionaron una perspectiva
completamente nueva y sus resultados se encuentran entre los m´as importantes de las matem´aticas.

2. 2 Nociones generales sobre funciones
especies vegetales y animales. Casi todo es susceptible de ser tratado a trav´es del planteamiento y estudio de una o varias
funciones que gobiernan los mecanismos internos de los procesos en todas las escalas y niveles.
1.2 Conceptos B´asicos
Variable La variable y es una variable dependiente de la variable x si existe una relaci´on, que puede estar dado por una
ecuaci´on, en donde el valor de x interviene directamente en el valor y. La variable x es una variable no relacionada con la
variable y si el valor de una no afecta directamente a la otra.
Funci´on Sea A el conjunto de valores que puede tomar una variable independiente, y sea B el conjunto de valores para
la variable dependiente. Si f es una regla de asociaci´on entre los elementos de A y B, entonces A, B y f determinan una
funci´on, si f asigna a cada elemento x ∈ A un ´unico elemento y ∈ B llamado f(x) o imagen de x bajo f.
f : A → B
x → f(x)
Dominio y Codominio Si se tiene una funci´on f definida de un conjunto A en un conjunto B, es decir: f : A → B,
entonces al conjunto A se le llama dominio, y al conjunto B se le llama codominio de la funci´on.
´Ambito Es el conjunto formado por las im´agenes de los elementos del dominio. Se puede denominar por Amb(f) el
´ambito de la funci´on f.
Preim´agenes e im´agenes A los elementos de A se les llama preim´agenes; y a los elementos de Amb(f) se les llama
im´agenes. La imagen es ´unica; no as´ı la preimagen.
Gr´afico Es el conjunto de pares ordenados (x,y).
Gr´afica Es el conjunto de puntos representados en el plano cartesiano.
Criterio Es una regla de asociaci´on entre los elementos A y B.
Monoton´ıa
• Una funci´on f : A → B es estrictamente creciente en un intervalo ]x1,x2[⊂ A si para cualquier par de n´umeros a,b
en ]x1,x2[ tal que a < b, entonces f(a) < f(b).
• Una funci´on f : A → B es estrictamente decreciente en un intervalo ]x1,x2[⊂ A si para cualquier par de n´umeros a,b
en ]x1,x2[ tal que a < b, entonces f(a) > f(b).
• Una funci´on f : A → B es constante en un intervalo ]x1,x2[⊂ A si para cualquier par de n´umeros a,b en ]x1,x2[ tal
que a < b, entonces f(a) = f(b).
Los intervalos en los cuales una funci´on es estrictamente creciente, estrictamente decreciente o constante se conocen como
intervalos de monoton´ıa.
Positividad y negatividad de una funci´on
• f(x) es positiva en un subconjunto M de A si para todos los valores x ∈ M , f(x) > 0.
• f(x) es negativa en un subconjunto M de A si para todos los valores x ∈ M , f(x) < 0.
Paridad de una funci´on Una funci´on f(x) con dominio A es:

3. 3
1. Par si f(−x) = f(x), ∀x ∈ A 2. Impar si f(−x) = −f(x), ∀x ∈ A
Interpretaci´on de una Gr´afica
Dada la gr´afica de una funci´on es posible determinar su dominio, ´ambito, intervalos de monoton´ıa y su signo.
1. En el eje x se puede observar el dominio de una funci´on, y en el eje y su ´ambito.
2. Una funci´on es estrictamente creciente si conforme x se desplaza a la derecha, f(x) se desplaza hacia arriba.
3. Una funci´on es estrictamente decreciente si conforme x se desplaza a la derecha, f(x) se desplaza hacia abajo.
4. Una funci´on es constante si su gr´afica se mantiene paralela al eje x
5. Una funci´on es positiva para los valores de x tales que f(x) se encuentra sobre el eje x
6. Una funci´on es negativa para los valores de x tales que f(x) se encuentra bajo el eje x
Dominio M´aximo
El dominio m´aximo real es el mayor subconjunto de R en el cual f(x) est´a definida. Hay que revisar:
1. Que no haya divisi´on por cero: hay que excluir todos los valores que hagan que los denominadores sean cero.
2. Que los argumentos de las ra´ıces de ´ındice par no sean n´umeros negativos: hay que considerar los valores para los
cuales el argumento sean mayor o igual a cero.
3. Que los argumentos de los logaritmos no sean n´umeros negativos: hay que considerar los valores para los cuales el
argumento sean mayor a cero.
Transformaciones de funciones
Traslaci´on vertical
1. La gr´afica de y = f(x)+c; c > 0 consiste en trasladar f(x), c unidades hacia arriba.
2. La gr´afica de y = f(x)−c; c > 0 consiste en trasladar f(x), c unidades hacia abajo.
Traslaci´on Horizontal
1. La gr´afica de y = f(x+c); c > 0 consiste en trasladar horizontalmente a f(x), c unidades hacia la izquierda.
2. La gr´afica de y = f(x−c); c > 0 consiste en trasladar horizontalmente a f(x), c unidades hacia la derecha.
Elongaci´on o compresi´on vertical
1. La gr´afica de y = cf(x); c > 1 consiste en una elongaci´on vertical en un factor c de la gr´afica de y = f(x).
2. La gr´afica de y = cf(x); 0 < c < 1 consiste en una compresi´on vertical en un factor
1
c
de la gr´afica de y = f(x).
Reflexi´on
1. La gr´afica de y = −f(x) consiste en una reflexi´on con respecto al eje x de la gr´afica de y = f(x)
2. Si la gr´afica de y = f(x) pasa por el punto (a,b) entonces la gr´afica de y = −f(x) pasa por el punto (a,−b)
3. La gr´afica de y = f(−x) consiste en una reflexi´on con respecto al eje y de la gr´afica de y = f(x)
4. Si la gr´afica de y = f(x) pasa por el punto (a,b) entonces la gr´afica de y = f(−x) pasa por el punto (−a,b)

4. 4 Nociones generales sobre funciones
Clases de funciones
Funci´on Lineal Sea f : R → R; f(x) = mx + b donde m
indica la pendiente y b el punto de intersecci´on mejor lla-
mado como intercepto. Su gr´afica es:
Funci´on Cuadr´atica Sea f : R → R; f(x) = (x+a)2 +b.
Su gr´afica es:
Funci´on C´ubica Sea f : R → R; f(x) = x3.
Su gr´afica es:
Funci´on radical Sea f : [0,+∞[→ R; f(x) =
√
x. Su
gr´afica es:

5. 5
Valor absoluto La gr´afica de y = |f(x)| consiste en la
gr´afica de:
f(x) =



f(x), si x ≥ 0
−f(x), si x < 0
Como se puede ver se trata b´asicamente de una re-
flexi´on parcial de la gr´afica de y = f(x): el trazo
por abajo del eje x se refleja con respecto al eje y.
Funci´on Inyectiva
Sea f : A → B, se dice que f es inyectiva si y solo si cada elemento del ´ambito tiene una y solo una preimagen.
• Se dice que si f es creciente en todo su dominio, entonces f es inyectiva.
• Se dice que si f es decreciente en todo su dominio, entonces f es inyectiva.
Funci´on Sobreyectiva
Sea f : A → B, se dice que f es sobreyectiva si y s´olo si el ´ambito de f es igual a su codominio.
Funci´on biyectiva
Se dice que una funci´on f : A → B es biyectiva si y s´olo si f es inyectiva y sobreyectiva.
1.3 Operaciones con funciones
Operaciones fundamentales
Sean f : A1 → R y g : A2 → R funciones. A1 y A2 subconjuntos de R. Se denota f + g una nueva funci´on que asocia a
cada x ∈ A1 ∩A1 con un ´unico elemento f(x)+g(x). Es decir
f ±g(x) = f(x)±g(x)
De igual manera se define la resta, multiplicaci´on.
Divisi´on Sean las funciones f(x) y g(x) definidas en su dominio m´aximo, A y B respectivamente, entonces
f
g
(x) =
f(x)
g(x)
.
Su dominio es A ∩ B siempre que g(x) = 0
Composici´on de Funciones Sean f : A → B, y g : B → C dos funciones reales. La funci´on compuesta f ◦g : A → C
est´a definida como la funci´on.
(g◦ f)(x) = g(f(x))

6. 6 Nociones generales sobre funciones
Funci´on Inversa
Toda funci´on f : A → B posee una relaci´on inversa de B en A. Esta relaci´on no es necesariamente una funci´on
Si f : A → B es una funci´on real; la funci´on inversa f−1 existe s´ı y s´olo s´ı f es biyectva.
∀ funci´on biyectiva se cumple que
f(f−1
(x)) = x
y
f−1
(f(x)) = x

7. 2 Funci´on Lineal
Definici´on 2.1 Una funci´on lineal es una funci´on cuyo dominio son todos los n´umeros reales y cuya expresi´on ´analitica
es un polinomio de primer grado.
f : R → R / f(x) = mx+b ∀ a,b ∈ R
El ´ultimo rengl´on se lee: f de R en R, tal que, f de equis es igual a mx+b
f : R −→ R, f(x) = 4x+8 m = 4, b = 8
f : R −→ R, f(x) = −1
2 x m = −1
2 , b = 0
f : R −→ R, f(x) = 1
3 m = 0, b = 1
3
Ejemplo 2.1
La funci´on f : R → R, f(x) = x, conocida como funci´on identidad tiene por gr´afica la recta que contiene al origen y
biseca los cuadrantes II y III.
La gr´afica de una funci´on de la forma y = mx, se puede obtener, a partir de la gr´afica de la funci´on y = x, mutiplicando la
coordenada y de cada uno de los puntos de la gr´afica y = x por el factor m.

8. 8 Funci´on Lineal
Gr´afique, en el mismo plano cartesiano, las funciones:
f : R → R, f(x) = πx h : R → R, h(x) = 2x
Ejemplo 2.2
SOLUCI ´ON:
Se sabe que las gr´aficas de h y de f contienen al origen adem´as tenemos que la gr´afica de h es la recta que contiene los pun-
tos en los cuales la cordenada y es el doble de la coordenada x, algunos puntos de esta gr´afica son (1,2), (−1,−2), (2,4).
La gr´afica de f se puede obtener como vimos anteriormente, multiplicando la segunda coordenada de la recta y = x por
π. Por la tanto la gr´afica de f contiene a los puntos (1,π),(−2,−2π),(π,π2).
Las gr´aficas de estas funciones son:
2.1 La pendiente de una recta
Cuando se conocen dos puntos de una recta (x1,y1) y (x2,y2) con x1 = x2, y1 = f(x1), y2 = f(x2) se cumple
y1 = mx1 + b ⇒ y1 − mx1 = b y y2 = mx2 + b
⇒ y2 −mx2 = b.
De lo anterior se tiene
y1 −mx1 = y2 −mx2
mx2 −mx1 = y2 −y1
m(x2 −x1) = y2 −y1
m = y2−y1
x2−x1
m es una constante para cualquier par de puntos distintos (x1,y1) y (x2,y2) m se llama pendiente de la recta.
En general se puede afirmar que las gr´aficas de las funci´on, f : R −→ R, f(x) = mx, tienen alguna de las siguientes

9. 9
formas:
2.1.1 ¿Qu´e representa m?
Considere la recta de ecuaci´on y = 5x+1. La pendiente de la recta es m = 5. Algunos valores de (x, f(x)) se representan
en la tabla.
x -2 -1 0 1 2 3
f(x) -9 -4 1 6 11 16
Los valores de y aumentan 5 unidades
el incremento en x es ∆x = 1
el incremento en y es ∆y = 5
En general:
Por cada unidad de incremento en la variable x, la variable y aumenta m unidades.
Simb´olicamente:
f(x+1)− f(x) = m
m =
∆x
∆y
A partir de la gr´afica y = mx, se puede construir la gr´afica y = mx + b, para ello basta hacer un traslaci´on vertical de |b|
unidades hacia arriba, si b > 0, y hacia abajo si b < 0.
2.2 Rectas paralelas
Dos rectas 1 : y1 = m1x +b1 y 2 : y2 = m2x +b2 son par-
alelas si sus pendientes son iguales.
1 y 2 ⇔ m1 = m2
Como 1 y 2 tienen igual pendiente entonces las rectas no
se intersecan, es decir, son paralelas.
1 : y = 4x−3 y 2 : y = 4x+1 son rectas paralelas.
Ejemplo 2.3

10. 10 Funci´on Lineal
2.3 Rectas perpendiculares
Dos rectas 1 : y1 = m1x+b1 y 2 : y2 = m2x+b2 son perpendiculares si m1 ·m2 = −1
1 y 2 ⊥ ⇔ m1 ·m2 = −1
1 : y = −2
3 x+6 y 2 : y = 3
2 x−7 son rectas perpendiculares.
Ejemplo 2.4

11. 3 Funci´on Cuadr´atica
3.1 Definiciones
Se llama funci´on cuadr´atica a la funci´on: f : R → R / f(x) = ax2 +bx+c donde a,b,c ∈ R y a = 0
Definici´on 3.1
f : R −→ R, f(x) = 4x2 +8x−2
f : R −→ R, f(x) = −1
2 x2 +7x
f : R −→ R, f(x) = 1
3 x2 −π
Ejemplo 3.1
• Otra forma de expresar la funci´on cuadr´atica:
La expresi´on y = ax2 +bx+c tambi´en se puede expresar en la forma:
y = a x+
b
2
−
b2 −4ac
4a
Algunas caracter´ısticas de la funci´on cuadr´atica se pueden estudiar m´as f´acilmente gracias a esta expresi´on (omi-
tiremos los pasos para llegar a esta expresi´on pero se puede obtener completando cuadrados).
3.2 Gr´afica de una funci´on cuadr´atica
La gr´afica de una funci´on cuadr´atica se llama par´abola. Es el conjunto de puntos del plano (x,y) donde
y = ax2 + bx + c. Para representar la funci´on cuadr´atica se tienen que considerar las siguientes caracter´ısticas de la
par´abola:

12. 12 Funci´on Cuadr´atica
3.2.1 Concavidad
Una manera sencilla de referirnos a la concavidad es hacia donde “abre” la par´abola.
a > 0 a < 0
3.2.2 V´ertice
Es el punto extremo de la gr´afica. Puede decirse que es el punto m´as bajo o m´as alto de la gr´afica.
Las coordenadas del v´ertice est´an dadas por el punto:
V =
−b
2a
,
−b2 −4ac
4a
Adem´as si la par´abola es c´oncava hacia arriba (a > 0) el v´ertice es un punto m´ınimo de esta curva, mientras que si la
par´abola es c´oncava hacia abajo (a < 0 el v´ertice es un punto m´aximo.
Se llama discriminante de la ecuaci´on ax2 +bx+c = 0 a la expresi´on b2 −4ac y se representa por ∆, as´ı ∆ = b2 −4ac por
tanto el v´ertice est´a dado por el punto:
V =
−b
2a
,
−∆
4a
En resumen:
a > 0 C´oncava hacia arriba V =
−b
2a
,
−∆
4a
es el punto m´ınimo.
a < 0 C´oncava hacia abajo V =
−b
2a
,
−∆
4a
es el punto m´aximo.

13. 13
El v´ertice de la par´abola que corresponde a la funci´on f : RtoR, f(x) = 2x2 +3x−27 esta dado por:
V =
−3
2·2
,
−(32 −4·2·−27)
4·2
=
−3
4
,
−225
8
Como la par´abola es c´oncava hacia arriba pues a = 2 > 0, entonces el punto V =
−3
4
,
−225
8
es su punto m´ınimo.
Ejemplo 3.2
3.2.3 Eje de simetr´ıa:
Se dice entonces que la recta x =
−b
2a
es un eje que divide a la par´abola en dos partes sim´etricas.
Eje de simetr´ıa x =
−b
2a
3.2.4 Intersecciones con los ejes
3.2.4.1 Intersecci´on con el eje Y El punto de intersecci´on de la gr´afica de una funci´on con el eje Y es (0,y). Dado
que f(0) = c entonces el punto de intersecci´on es (0,c).
La par´abola corta al eje Y en (0,c)
3.2.4.2 Intersecci´on con el eje X: El punto de intersecci´on de la gr´afica de una funci´on con el eje X es un punto
donde f(x) = 0 por tanto hay que resolver la ecuaci´on:
0 = ax2
+bx+c
Esta ecuaci´on es de grado 2 y puede tener en los n´umeros reales 2 soluciones, 1 soluci´on o ninguna soluci´on.
1. Si ∆ < 0 entonces la ecuaci´on no tiene soluci´on y la par´abola no corta al eje X.
2. Si ∆ = 0 la ´unica soluci´on es x =
−b
2a
. Por tanto el punto de intersecci´on es
−b
2a
,0 que tambi´en es el v´ertice de
la par´abola.
3. Si ∆ = 0 la ecuaci´on tiene dos soluciones x1 =
−b−
√
∆
2a
y x2 =
−b+
√
∆
2a
.
3.2.5 ´Ambito de una funci´on cuadr´atica
Como se analiz´o antes el v´ertice es un punto m´aximo o m´ınimo seg´un la par´abola sea c´oncava hacia arriba o hacia abajo.
Por esto cualquier imagen se compara con
−∆
4a
que es el valor de la ordenada en V =
−b
2a
,
−∆
4a
.
Entonces:
C´oncavidad V´ertice ´Ambito
a > 0 hacia arriba V =
−b
2a
,
−∆
4a
−∆
4a
,+∞
a < 0 hacia abajo V =
−b
2a
,
−∆
4a
−∞,
−∆
4a

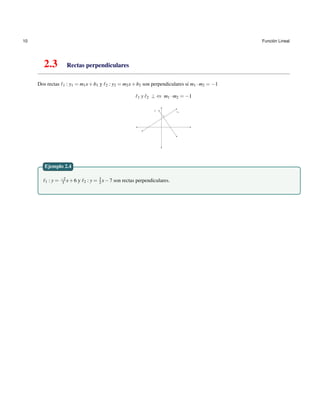
14. 14 Funci´on Cuadr´atica
3.2.6 An´alisis de la funci´on cuadr´atica a partir de la gr´afica.
• f(x) = ax2 +bx+c, con a > 0
´Ambito :
−∆
4a
,+∞
Creciente :
−b
2a
,+∞
Decreciente: −∞,
−b
2a
V: punto m´ınimo.
f(x) < 0 si x ∈]x1,x2[
f(x) > 0 si x ∈]−∞,x1[∪]x2,∞[
f(x) = 0 si x ∈ {x1,x2}
• f(x) = ax2 +bx+c, con a < 0
´Ambito : −∞,
−∆
4a
Creciente : −∞,
−b
2a
Decreciente:
−b
2a
,+∞
V: punto m´aximo.
f(x) < 0 si x ∈]−∞,x1[∪]x2,∞[
f(x) > 0 si x ∈]x1,x2[
f(x) = 0 si x ∈ {x1,x2}

15. 4 Funciones exponenciales y
logar´ıtmicas
4.1 Funci´on exponencial
4.1.1 Previos
Antes de iniciar este tema es importante recordar las leyes de potencias:
1. Todo n´umero elevado a 1 es igual al mismo n´umero.
x1
= x
2. Todo n´umero elevado a 0 es 1.
x0
= 1
3. Todo n´umero elevado a un n´umero negativo es igual a 1 entre la base elevada al mismo exponente, pero positivo.
x−n
=
1
xn
4. En la multiplicaci´on de n´umeros de igual base, se conserva la base y se suman los exponentes.
xn
xm
= xn+m
5. En la divisi´on de n´umeros de igual base, se conserva la base y se restan los exponentes (el resultado de la resta se
coloca donde estaba el n´umero de mayor grado)
xm
xn
= xm−n
6. Potencia de una potencia: Se multiplican los exponentes.
(xn
)m
= xn.m
7. Un n´umero elevado a una fracci´on puede transformarse a una ra´ız; el denominador se convierte en el ´ındice de la
ra´ız y el n´umerador en el exponente de la base.
x
m
n = n
√
xm

16. 16 Funciones exponenciales y logar´ıtmicas
4.1.2 Funci´on exponencial
La funci´on exponencial est´a definida por la ecuaci´on f(x) = ax, a > 0 y a = 0 donde la constante a, se llama base y el
exponente x, es una variable.
f(x) = ax,a > 1 No interseca al eje x
Interseca a y en (0,1)
Es creciente
As´ıntota en x por la izquierda
Dominio: R ´Ambito: R+
Biyectiva
f(x) = ax,0 < a < 1
No interseca al eje x
Interseca a y en (0,1)
Es decreciente
As´ıntota en x por la derecha
Dominio: R ´Ambito: R+
Biyectiva
4.1.3 Caracter´ısticas de la funci´on exponencial
1. f recorre todo el eje x, su dominio m´aximo es R
2. El ´ambito de f es R+. Es decir, ax > 0; ∀x ∈ R
3. f interseca el eje y en 1. Es decir, la gr´afica de f pasa por el punto (0,1), dado que a0 = 1; ∀a = 0
4. f no interseca el eje x dado que f(x) > 0; ∀x ∈ R
5. f posee as´ıntota horizontal y = 0. Es decir, cuando x → ±∞, f(x) → 0. Esto significa que cuando x es suficiente-
mente grande o peque˜na, su imagen tiende a cero.
6. Para a > 1, f es estrictamente creciente y para 0 < a < 1, f es estrictamente decreciente. Esto significa que f es
inyectiva.
4.1.4 Gr´aficas de Funciones exponenciales
A partir de la funci´on exponencial est´andar y de los conocimientos sobre transformaciones de gr´aficas, podemos obtener
buenos bosquejos de otras exponenciales.

17. 17
Transformaci´on una unidad hacia la izquierda, y = (x+1) =
ax+1, a > 1
Transformaci´on una unidad hacia la derecha, y = f(x) =
ax−1, a > 0
Note que cuando la suma o resta est´a elevada, junto a la x, las transformaciones son hacia la izquierda y derecha respecti-
vamente, sobre el eje x.
Traslaci´on una unidad hacia arriba,
y = f(x)+1 = ax +1, a > 1
Traslaci´on una unidad hacia abajo,
y = f(x)−1 = ax −1, a > 1

18. 18 Funciones exponenciales y logar´ıtmicas
Note que cuando la suma o resta est´a junto a la x, sin estar elevado, las transformaciones son hacia arriba y abajo respec-
tivamente, sobre el eje x.
Reflexi´on de una gr´afica y = ax,
−ax, a > 1
Cuando f(x) tiene un menos adelante, la funci´on se refleja.
4.1.5 Exponencial natural
La funci´on exponencial con base e es:
f : R → R, tal que f(x) = ex
Donde e ≈ 2,7182828
Dado que 2 < e < 3 la gr´afica satisface todas las caracter´ısticas de las funciones exponenciales con base mayor que 1, la
gr´afica de la esponencial natural es la siguiente:
4.2 Funci´on logar´ıtmica
Una funci´on logar´ıtmica con base a, a ∈ R+, a = 1, es una funci´on que se denota
f(x) = loga x y est´a definida como:
loga x = y ⇔ ax
= x
Ejemplo. Calcule el valor de log2 32, log3
1
81 , log0,01

19. 19
Soluci´on
1. log2 32 = y ⇔ 2y = 32 ⇒ y = 5. O sea, log2 32 = 5
2. log3
1
81 = n ⇔ 3n = 3−4 ⇒ n = −4. O sea log3
1
81 = −4
3. log0,01 = z ⇔ 10z = 0,01 ⇔ 10z = 10−2 ⇒ z = −2 = log0,01.
4.2.1 Propiedades
Dado que a > 0, a = 1
1. loga 1 = 0 2. loga a = 1
Es posible considerar dos casos:
f(x) = loga x, a > 1
f(x) = loga x, 0 < a < 1
Algunas caracter´ısticas de la funci´on logar´ıtmica son:
1. f recorre todo el eje x positivo, su dominio m´aximo es R
2. El ´ambito de f es R. Es decir, loga x ∈ R;∀x > 0
3. f interseca el eje x en 1. Es decir, la gr´afica de f pasa por el punto (1,0), dado que loga 1 = 0 porque a0 = 1;
∀x = 0

20. 20 Funciones exponenciales y logar´ıtmicas
4. f no interseca el eje y dado que ax > 0; ∀x ∈ R
5. f posee as´ıntota vertical x = 0. Es decir, cuando x → 0+, f(x) → ±∞. Esto significa que cuando x es suficientemente
grande o peque˜na, su imagen tiende a cero.
6. Para a > 1, f es estrictamente creciente y para 0 < a < 1, f es estrictamente decreciente.
4.2.2 Gr´aficas de funciones logar´ıtmicas
Es importante notar que estas transformaciones pueden implicar cambios en las caracter´ısticas anteriores.
Traslaci´on una unidad hacia la izquierda,
y = f(x+1) = loga(x+1), a > 1
Traslaci´on una unidad hacia la derecha,
y = f(x−1) = loga(x−1), a > 1
Traslaci´on una unidad hacia arriba,
y = f(x+1) = loga x+1, a > 1

21. 21
Traslaci´on una unidad hacia abajo,
y = f(x−1) = loga(x−1), a > 1
Reflexi´on de la gr´afica y = loga x, y = −loga x, a > 1
4.2.3 Logaritmos naturales
La funci´on logaritmo con base e, se denota f(x) = lnx y est´a definida como:
lnx = y ⇔ ey
= y
y = lnx y = ex
4.2.3.1 Composici´on de la exponencial y logar´ıtmica Una funci´on y su inversa complen las propiedades: f−1(f(x)) =
x; ∀x ∈ Df y f(f−1) = x∀x ∈ Df−1 , al alpicar estas propiedades al caso de las funciones exponenciales f(x) = ax y
logar´ıtmica f−1(x) = loga x obtenemos:
1. loga ax = x; x ∈ R
2. aloga x = x; x > 0

22. 22 Funciones exponenciales y logar´ıtmicas
4.2.4 Propiedades de los logaritmos
1. El logaritmo del producto es igual a la suma de los factores de los logaritmos de cada factor
loga(x.y) = loga x+loga y
2. El logaritmo del cociente es igual a la resta del logaritmo del numerador y el logaritmo del denominador
loga
x
y
= loga x−loga y
3. El logaritmo de una potencia es igual al producto del exponente y el logaritmo de la base de la potencia
loga(xn
) = n.loga x
4. Cambio de base: Es posible reescribir un logartimo de base a a una expresi´on de logaritms en base n
loga b =
logn b
logn a

23. Bibliograf´ıa
[1] Arias, F y Poveda, W. (2011). Matem´atica Elemental. 1era Edici´on, Costa Rica: Edit. UCR.
[2] Stewart, J. (2001). Prec´alculo. 3era Edici´on. M´exico: International Thomson Editores.
[3] Sancho, L y Blanco, R. (2012). Matem´atica para la Ense˜nanza Media. 1era Edici´on, Costa Rica: Edit. UCR.
[4] Bartle, R. (1990). Introducci´on al An´alisis Matem´atico. 2da Edici´on. M´exico: Limusa.
[5] Porras N., V. (2005). Matem´atica 11mo; recopilaci´on de ejercicios, nuevo temario unificado. 3ra Ed. Publicaciones
Porras y Gamboa. San Jos´e, Costa Rica.
[6] Swokowski, E y Cole. J. (2002). ´Algebra y Trigonometr´ıa con Geometr´ıa Anal´ıtica. 10ma Edici´on. M´exico: Thom-
son Editores, S.A.