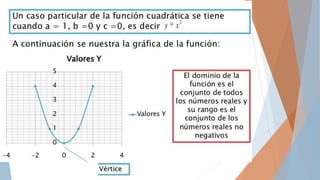
El documento trata sobre las funciones reales de una variable. Brevemente describe que el término "función" fue utilizado por primera vez por Descartes en 1637 y luego Leibniz lo usó en 1694 para referirse a varios aspectos de una curva. Finalmente, Dirichlet dio la definición más generalizada de función en 1829.

1. Funciones Reales en una Variable

2. El término función fue usado por primera vez en
1637 por el matemático francés René Descartes
para designar una potencia de la variable x.
En 1694 el matemático alemán Gottfried Wilhelm
Leibniz utilizó el término para referirse a varios
aspectos de una curva, como su pendiente.
Hasta recientemente, su uso más generalizado ha
sido el definido en 1829 por el matemático
alemán, J.P.G. Lejeune-Dirichlet (1805-1859)
𝒙 𝒏
Un poco de Historia…

3. FUNCIÓN INYECTIVA
Para determinar si una función es Inyectiva, graficamos la
función por medio de una tabla de pares ordenados. Luego
trazamos líneas horizontales para determinar si las y (las
ordenadas) se repiten o no.
Definiciones Elementales

4. FUNCIÓN INYECTIVA
A B
C D

5. FUNCIÓN SOBREYECTIVA

6. FUNCIÓN SOBREYECTIVA
A B C
D E F
G H I

7. FUNCIÓN BIYECTIVA

8. FUNCIÓN BIYECTIVA
A B C
D E F
G H I

9. EN GENERAL…

10. Correspondencia
 La noción de correspondencia representa un papel fundamental en el
concepto de relación-función.
 En nuestras vidas cotidianas frecuentemente hemos tenido experiencia
con correspondencias o relaciones.
Ejemplos:
 En un almacén a cada articulo le corresponde un precio.
 A cada nombre del directorio le corresponde uno o varios números.
 A cada estudiante le corresponde un promedio de calificaciones.

11. La palabra “función” es utilizada en nuestro
lenguaje común para expresar que algunos
hechos dependen de otros. Así, la idea
matemática de función no es un concepto
nuevo, sino una formalización de nuestra idea
intuitiva
Función

12. Una función es una relación a la que se le añade restricción.
Dados dos conjuntos N y M, se dice que f es una función definida en el conjunto
N sí y solo si a cada elemento de N se le asigna uno y sólo un elemento de M.
Se representa por: f = N ⇾ M
El conjunto N recibe indistintamente los nombres de
conjunto origen, conjunto inicial, dominio de la función, o
campo de existencia de la función, y se representa por
Dm(f).
Relación
Una relación es una correspondencia entre un conjunto
llamado dominio con un segundo conjunto llamado rango
de tal manera que a cada elemento del dominio le
corresponde uno o varios elementos del rango o recorrido.
Función
Toda función es una
relación, pero no toda
relación es una función.

13. El dominio de una función es el conjunto de todas las
coordenadas x de los puntos de la gráfica de la función;
Los valores en el dominio usualmente están asociados con
el eje horizontal (el eje x).
El rango es el conjunto de todas las coordenadas en el eje
y; los valores del rango con el eje vertical (el eje y).
Dominio y Rango o Recorrido de una función

14. Dominio y Recorrido usando Método de Diagrama Sagital

15. ¿Cual es el Dominio y Recorrido de la
siguiente función?
  4 2f x x  
 
2
4 2y x  
Dominio
Recorrido
2 0x  
2x  
   2;Dom f   
4 2y x  
 
2
4 2y x  
4 2y x  
   Re 4;c f  




Buscar condiciones para la variable Buscar condiciones para la variablex y

16. Representación Gráfica
Plano CartesianoMétodo de Diagrama Sagital
A IR
B IR
 y f x
x
  ;P x f x

17. Al trazar una línea recta perpendicular al eje y, ésta debe cortar a la
gráfica solamente en un punto para que sea una Función.
Prueba de la Recta Vertical

18. ¿ Cuál es Función ?

19. Clasificación de las Funciones
Estas funciones las
estudiaremos en otro
lapso

20. Clasificación de las funciones
 f x mx b Función Lineal
Función Cuadráticas   2
f x ax bx c  
Función Racional  
1
f x
x
 donde 0x 
Función Valor Absoluto  f x x
donde
0
0 0
0
x si x
x si x
x si x


 
 

21. Función Lineal
Función Cuadráticas
Función Racional
Función Valor Absoluto

22. FUNCIÓN INVERSA

23. FUNCIÓN INVERSA

24. Función inversa
1
f
En una función inversa el
dominio, será el rango o
recorrido y el rango pasa a
ser el dominio

25. Ejemplo
Hallar la inversa y grafica de la siguiente función   2 1f x x 
Solución Para hallar la inversa de la función debemos despejar la variable x
2 1y x 
1 2y x 
1
2
y
x

 Por lo tanto
 1 1
2
x
f x 


26. Y ambas grafica en el mismo plano cartesiano son
  12  xxf
 
1
2
x
f x



27. Paridad de una función
Decimos que una función es par siempre que
para todo valor de la variable independiente
perteneciente al dominio se cumpla que:
Funciones pares
   xfxf 

28. Función Impar Decimos que una función es impar siempre que
para todo valor de la variable independiente
perteneciente al dominio se cumpla que:
   f x f x  
El carácter par o impar de una función es lo que
conocemos como su paridad. Las funciones que
no son ni pares, ni impares, carecen de paridad.
Ejemplo
Función sin paridad
𝐹 𝑥 = 𝑥
1
2

29. Ejemplos 1.- Para cada una de las siguientes relaciones,
determine Dominio, Recorrido para que sea
función
  12
 xxf
 
1
1
x
f x
x



  2 1f x x  
a)
b)
c)

30. Función Afín o Lineal

31. El dominio de la función afín, al igual que el rango son todos los números reales
x y
-2 -8
-1 -6
0 -4
1 -2
2 0

32. Función Cuadrática

34. V=
Ecuación del Vértice

35. x y
-2 3
-1 0
0 -1
1 0
2 3
Domy=R
Rgoy=[-1,+ ∞ )
V=
V= (0,-1)
a=1
b=0
c=-1

36. Función Valor Absoluto
La función valor absoluto asocia a cada número su valor
absoluto, es decir su valor prescindiendo del signo.

37. Ejemplo
DomF(x)= R Rgo F(x)= 𝑅+

38. Función Racional

39. Ejemplo