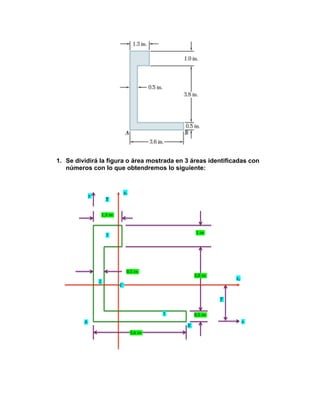
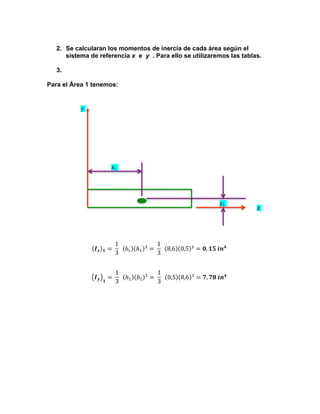
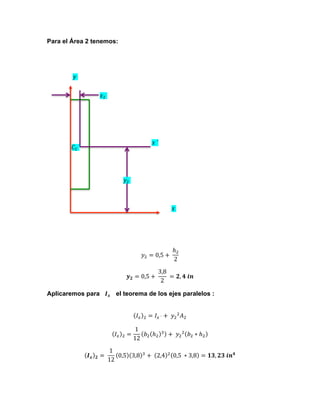
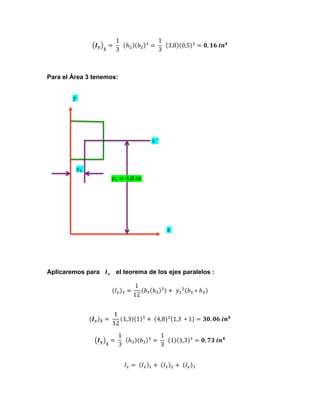
1. La figura se divide en 3 áreas numeradas y se calculan los momentos de inercia de cada área con respecto a los ejes x e y usando tablas. 2. Los momentos de inercia totales son Ix = 18.13 in4 y Iy = 4.53 in4. 3. La ubicación del centroide es x = 0.91 in y y = 2.25 in.

1. 1. Se dividirá la figura o área mostrada en 3 áreas identificadas con
números con lo que obtendremos lo siguiente:
!!
!!
!!
1,3!!"!
1!!"!
3!
0,5!!"!
2!
3,8!!"!
!!
!!
!!
1!
!!
0,5!!"!
!!
3,6!!"!
!!

2. 2. Se calcularan los momentos de inercia de cada área según el
sistema de referencia x e y . Para ello se utilizaremos las tablas.
3.
Para el Área 1 tenemos:
!!
!! !
!! !
𝑰𝒙
𝑰𝒚
𝟏
𝟏
1
= 𝑏! ℎ!
3
!
1
= 8,6 0,5
3
!
= 𝟎, 𝟏𝟓 𝒊𝒏 𝟒
1
= ℎ!
3
!
1
= 0,5 8,6
3
!
= 𝟕, 𝟕𝟖 𝒊𝒏 𝟒
𝑏!
!!

3. Para el Área 2 tenemos:
!!
!! !
!!´
!! !
!! !
!!
𝑦! = 0,5 +
𝒚 𝟐 = 0,5 +
Aplicaremos para
𝐼!
𝟐
3,8
= 𝟐, 𝟒 𝒊𝒏
2
𝑰 𝒙 el teorema de los ejes paralelos :
𝐼!
𝑰𝒙
ℎ!
2
=
!
=
!
= 𝐼! ´ + 𝑦! ! 𝐴!
1
𝑏 ℎ
12 ! !
1
0,5 3,8
12
!
!
+ 2,4
+ 𝑦! ! 𝑏! ∗ ℎ!
!
0,5 ∗ 3,8 = 𝟏𝟑, 𝟐𝟑 𝒊𝒏 𝟒

4. 𝑰𝒚
𝟐
1
= ℎ!
3
𝑏!
!
1
= 3,8 0,5
3
!
= 𝟎, 𝟏𝟔 𝒊𝒏 𝟒
Para el Área 3 tenemos:
!!
!!´
!! !
!! = 4,8!!"!
!!
𝑰 𝒙 el teorema de los ejes paralelos :
Aplicaremos para
𝐼!
𝑰𝒙
𝟑
𝑰𝒚
=
𝟑
!
=
1
𝑏 ℎ
12 ! !
1
1,3 1
12
1
= ℎ!
3
!
!
+ 4,8
+ 𝑦! ! 𝑏! ∗ ℎ!
!
1,3 ∗ 1 = 𝟑𝟎, 𝟎𝟔 𝒊𝒏 𝟒
𝑏!
!
1
= 1 1,3
3
𝐼! = 𝐼!
!
+ 𝐼!
!
+ 𝐼!
!
= 𝟎, 𝟕𝟑 𝒊𝒏 𝟒
!

5. 𝑰 𝒙 = 0,15 + 13,23 + 30,06 = 𝟒𝟑, 𝟒𝟒 𝒊𝒏 𝟒
𝐼! = 𝐼!
!
+ 𝐼!
!
+ 𝐼!
!
𝑰 𝒙 = 7,78 + 0,16 + 0,73 = 𝟖, 𝟔𝟕 𝒊𝒏 𝟒
Los momentos de Inercia de los ejes x e y son los siguientes:
𝐼! = 43,44 𝑖𝑛! ; 𝐼! = 8,67 𝑖𝑛!
𝑨 𝒕 = 𝐴! + 𝐴! + 𝐴! = 1,8 + 1,9 + 1,3 = 𝟓 𝒊𝒏 𝟐
Aplicaremos el Teorema de los ejes paralelos para determinar los
momentos de inercia centroidales, por lo tanto:
𝐼! = 𝐼!! + 𝑦 ! 𝐴!
𝑰 𝒙 𝒄 = 𝐼! − 𝑦 ! 𝐴! = 43,44 − 2,25
!
5 = 𝟏𝟖, 𝟏𝟑 𝒊𝒏 𝟒
𝐼! = 𝐼!! + 𝑥 ! 𝐴!
𝑰 𝒚 𝒄 = 𝐼! − 𝑥 ! 𝐴! = 8,67 − 0,91
!
5 = 𝟒, 𝟓𝟑 𝒊𝒏 𝟒
4. Ubicación del Centroide
𝑥 =
𝑥! 𝐴! + 𝑥! 𝐴! + 𝑥! 𝐴!
𝐴! + 𝐴! + 𝐴!
Teniendo en cuenta que:
𝑥! = 1,8 𝑖𝑛
𝑥! = 0,25 𝑖𝑛
𝑥! = 0,65 𝑖𝑛
𝐴! = 3,6 ∗ 0,5 𝑖𝑛!
𝐴! = 0,5 ∗ 3,8 𝑖𝑛!
𝐴! = 1,3 ∗ 1 𝑖𝑛!

6. 𝒙 =
1,8 3,6 ∗ 0,5 + 0,25 0,5 ∗ 3,8 + 0,65 1,3
= 𝟎, 𝟗𝟏 𝒊𝒏
1,8 + 1,9 + 1,3
𝑦 =
𝑦! 𝐴! + 𝑦! 𝐴! + 𝑦! 𝐴!
𝐴! + 𝐴! + 𝐴!
Teniendo en cuenta que:
𝑦! = 0,25 𝑖𝑛
𝑦! = 2,4 𝑖𝑛
𝑦! = 4,8 𝑖𝑛
𝐴! = 3,6 ∗ 0,5 𝑖𝑛!
𝐴! = 0,5 ∗ 3,8 𝑖𝑛!
𝐴! = 1,3 ∗ 1 𝑖𝑛!
𝒚 =
0,25 3,6 ∗ 0,5 + 2,4 0,5 ∗ 3,8 + 4,8 1,3
= 𝟐, 𝟐𝟓 𝒊𝒏
1,8 + 1,9 + 1,3