Este documento presenta un trabajo práctico sobre la separación de pérdidas en el hierro utilizando el aparato de Epstein. Explica que las pérdidas en el hierro se componen de pérdidas por histéresis y por corrientes de Foucault. Describe un método para determinar experimentalmente estas componentes variando la frecuencia a inducción máxima constante y trazando una gráfica de la potencia entregada al hierro por ciclo en función de la frecuencia. La ordenada en el origen de esta gráfica dará la p

1. Universidad Tecnológica Nacional
Cátedra: INSTRUMENTO Y MEDICIONES
Facultad Regional Santa Fe ELECTRICAS
Universidad Tecnológica Nacional
Facultad Regional Santa Fe
Instrumento y Mediciones Eléctricas
TRABAJO PRÁCTICO DE LABORATORIO Nº10
“Separación de perdidas en el hierro con el
aparato de Epstein”
Página 1 de 5

2. Universidad Tecnológica Nacional
Cátedra: INSTRUMENTO Y MEDICIONES
Facultad Regional Santa Fe ELECTRICAS
Alumno: ____________________________________________________Año:_______
Fecha de realización:_________Fecha de entrega:_________Fecha de visado_______
TRABAJO PRÁCTICO Nº10:
Separación De Pérdidas En El Hierro Con El Aparato De Epstein:
Aun cuando la perdida total en el hierro suele ser cuestión de principal importancia en el
diseño de aparatos electromagnéticos de C.A, la reducción de dicha perdida total solo
puede realizarse cuando se conocen los valores relativos de las componentes
correspondientes a las histéresis y a las corrientes de FOUCAULT. Si predominan la
componente correspondiente a las corrientes de FOUCAULT y se puede disponer de
láminas más delgadas, la utilización de estas reducirá la pérdida total. En cambio, si
predomina la pérdida por histéresis, es inútil cambiar el espesor de las láminas. Por tanto
convendrá que el primer paso hacia la reducción de la perdida total sea disponer de un
medio sencillo para determinar la división de la pérdida total en el hierro entre ambas
componentes.
Método A Utilizar.
Toda medida directa de la perdida de potencia en el hierro da necesariamente la perdida
total pero la división en las dos componentes puede determinarse experimentalmente si se
posee un generador que de una forma de onda esencialmente sinusoidal y cuya velocidad
se pueda regular.
Este generador alimenta un circuito de ensayo idéntico al utilizado en la determinación e
pérdidas con el aparato de Epstein, midiéndose la potencia entregada al hierro la tensión y
la frecuencia
Así entonces, realizando una serie de medidas diferentes manteniendo contaste la relación
f emi
f (para que Bmáx se mantenga también constante) a lo largo de un intervalo de
frecuencia que se extienda todo lo posible hasta una frecuencia casi nula, se tendrá los
P
datos necesarios. Estos consisten en la potencia entregada al hierro por ciclo fe , la
f
Pfe = F ( f )
frecuencia f, y la inducción máxima Bmax. Con ello se traza una gráfica f que
extrapolada hasta la frecuencia cero nos dará entonces la energía por histéresis por ciclo.
Ph Pp
Multiplicado los valores de y
ciclos f x se obtienen las pérdidas Ph y Pp
correspondiente a dicha frecuencia, a Bmax= constante.
Página 2 de 5

3. Universidad Tecnológica Nacional
Cátedra: INSTRUMENTO Y MEDICIONES
Facultad Regional Santa Fe ELECTRICAS
Justificación Del Método:
Las perdidas en el hierro se componen de las pérdidas por histéresis (Ph) y las perdidas por
corrientes de Foucault o parásitas (Pp) es decir:
Pfe = Ph + Pp [W / kg ](1)
Esta separación de pérdidas debido al hecho que estas primeras componentes varía
linealmente mientras que las ultimas lo hacen cuadrática mente con la frecuencia.
Ph = K 1 . f [W / kg ]( 2)
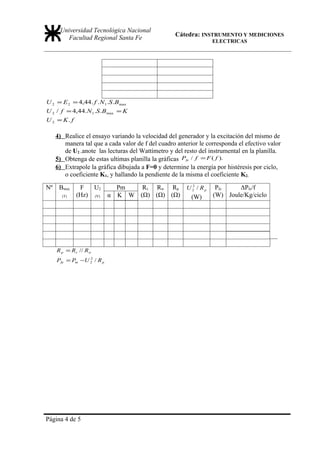
Pp = K 2 . f 2
[W / kg ](3)
Donde K1 y K2 son factores cuyos valores dependen de la clase del material, de la
construcción de la muestra, y de la inducción magnética máxima.
Es decir, dividiendo la ecuación (1), expresada por sus componentes, por la frecuencia f.
Pfe / f = K 1 + K 2 . f [ joule / Kg / ciclos ]( 4)
Resulta evidente que la componente correspondiente a la histéresis de la energía total por
ciclo Pfe/f es independiente de la frecuencia y la correspondiente a las corrientes de Foucalt
es función lineal de la frecuencia. Si se mide la perdida a una inducción magnética máxima
constante dada y sé varia la frecuencia, la grafica de la perdida por ciclos en función de la
frecuencia, si se cumple la relación teórica (4), debe ser una recta. Su ordenada en el origen
da la perdida por histéresis por ciclo K1 y la pendiente de la recta es el coeficiente K2.
Guía Para El Desarrollo Del Práctico:
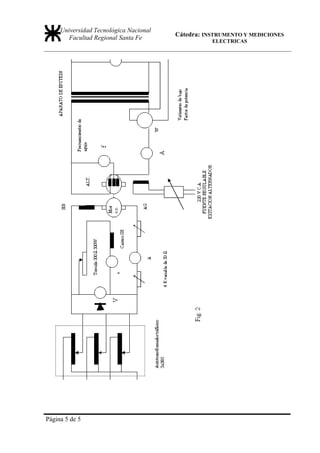
1) Arme el circuito de la fig2
2) Realice un inventario del instrumental utilizado
3) Cálculos previos de Bmax.
F(Hz) U2(V)
Página 3 de 5

4. Universidad Tecnológica Nacional
Cátedra: INSTRUMENTO Y MEDICIONES
Facultad Regional Santa Fe ELECTRICAS
U 2 = E 2 = 4,44. f .N 1 .S .Bmax
U 2 / f = 4,44.N 1 .S .Bmax = K
U 2 = K. f
4) Realice el ensayo variando la velocidad del generador y la excitación del mismo de
manera tal que a cada valor de f del cuadro anterior le corresponda el efectivo valor
de U2 .anote las lecturas del Wattímetro y del resto del instrumental en la planilla.
5) Obtenga de estas ultimas planilla la gráficas Pfe / f = F ( f ).
6) Extrapole la gráfica dibujada a F=0 y determine la energía por histéresis por ciclo,
o coeficiente K1, y hallando la pendiente de la misma el coeficiente K2.
Nº Bmax F U2 Pm Rv Rw Rp U 2 / R p
2
Pfe ΔPfe/f
(T) (Hz) (V) α K W (Ω) (Ω) (Ω) (W) (W) Joule/Kg/ciclo
R p = Rv // Rw
Pfe = Pm −U 2 / R p
2
Página 4 de 5

5. Universidad Tecnológica Nacional
Cátedra: INSTRUMENTO Y MEDICIONES
Facultad Regional Santa Fe ELECTRICAS
Página 5 de 5