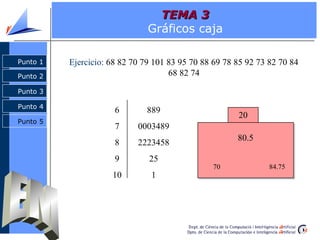
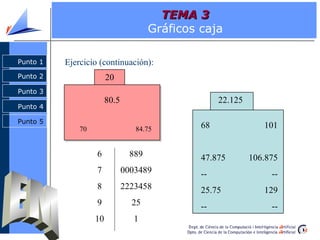
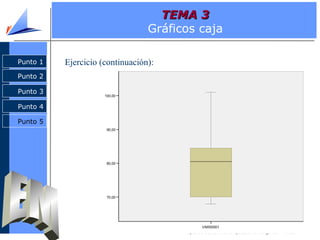
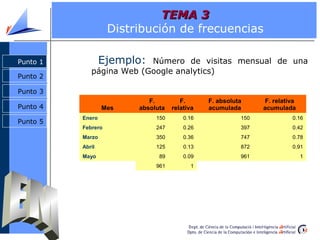
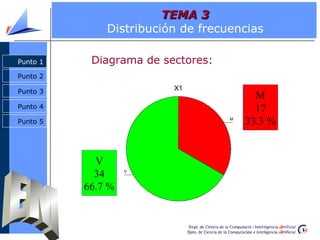
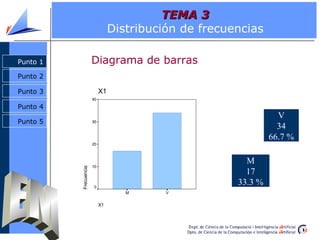
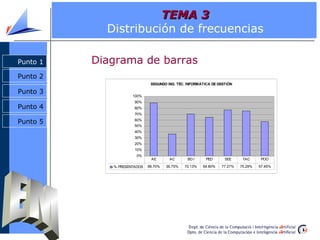
El documento aborda la estadística descriptiva, incluyendo distribución de frecuencias, parámetros estadísticos de centralización, posición y dispersión, y diversas representaciones gráficas como histogramas y diagramas de barras. Se presentan definiciones y ejemplos sobre cálculos de frecuencias absolutas y relativas, así como la diferencia entre media y mediana. Además, se explican conceptos relacionados con la forma de las distribuciones y la construcción de gráficos como diagramas de caja y gráficos de tallos y hojas.

1. TEMA 3
Estadística descriptiva
Punto 1
Punto 2
Punto 3
Estadística
Punto 4
Punto 5
INGENIERÍA MULTIMEDIA
Violeta Migallón

2. TEMA 3
Estadística descriptiva
Punto 1 Distribución de frecuencias
Punto 2
Parámetros y estadísticos de
Punto 3
centralización, posición y dispersión
Punto 4
Forma
Punto 5
Gráficos caja
Práctica
EXPLICACIÓN EN LABORATORIO

3. TEMA 3
Estadística descriptiva
Punto 1 Una vez recogidos los datos deben
Punto 2 procesarse de tal manera que pueda
Punto 3
observarse cualquier patrón
significativo
Punto 4
Punto 5 La estadística descriptiva permite
analizar y sintetizar la información
aportada por los datos

4. TEMA 3
Distribución de frecuencias
Punto 1 Frecuencia absoluta
Punto 2
Frecuencia relativa
Punto 3
Punto 4
Histograma de frecuencias
Punto 5 Diagrama de sectores
Diagrama de barras
EJEMPLO ACLARATORIO

5. TEMA 3
Distribución de frecuencias
Punto 1 Distribución de frecuencias absolutas:
Punto 2 • Lista de clases o categorías de datos con el número de
valores que hay en cada una de ellas
Punto 3
Punto 4 Distribución de frecuencias relativas:
Punto 5 • Se calcula dividiendo cada frecuencia absoluta entre el
número total de elementos clasificados
EJEMPLO ACLARATORIO

6. TEMA 3
Distribución de frecuencias
Punto 1 Ejemplo:Número de visitas mensual de una
página Web (Google analytics)
Punto 2
Punto 3
F. F. F. absoluta F. relativa
Punto 4 Mes absoluta relativa acumulada acumulada
Enero 150 0.16 150 0.16
Punto 5
Febrero 247 0.26 397 0.42
Marzo 350 0.36 747 0.78
Abril 125 0.13 872 0.91
Mayo 89 0.09 961 1
961 1

7. TEMA 3
Distribución de frecuencias
Punto 1 Frecuencia absoluta: frecuencia en la
Punto 2 tabla
Punto 3
Frecuencia relativa: porcentaje/100
Punto 4
Punto 5
X1: sexo (CPREYES)
Frecuencia Porcentaje Porcentaje
acumulado
M 17 33,3 33,3
V 34 66,7 100,0
Total 51 100,0

8. TEMA 3
Distribución de frecuencias
Punto 1 Frecuencia absoluta acumulada: suma
Punto 2 de frecuencias en la tabla hasta la
Punto 3
categoría correspondiente
Punto 4 Frecuencia relativa acumulada:
Punto 5 porcentaje acumulado/100
Nivel de uso de Internet para obtención de recursos
Porcentaje
Frecuencia Porcentaje acumulado
Ninguno 5 8.9 8.9
Ocasional 12 21.4 30.4
Mensual 10 17.9 48.2
Semanal 18 32.1 80.4
A diario 11 19.6 100.0
Total 56 100.0

9. TEMA 3
Distribución de frecuencias
Punto 1 Distribución de frecuencias agrupadas:
Se suelen utilizar para variables cuantitativas o
Punto 2
variables que contienen muchos datos distintos
Punto 3  Previamente se divide el rango de la muestra en
Punto 4 intervalos disjuntos que denominaremos intervalos de
clase
Punto 5
 Estos intervalos se suelen representar por el valor
central o punto medio que se denomina marca de clase.
 Generalmente se consideran los intervalos de igual
longitud, cerrados por la izquierda y abiertos por la
derecha
 Sin embargo podrían ser de amplitud variable

10. TEMA 3
Distribución de frecuencias
Punto 1 Ejemplo: distribución de frecuencias agrupadas
Punto 2 DATOS:
Punto 3 2 4 5 9 10 24 27 39 47 54 55 56 59 60 62 76 77
79 80 85 91 91 92 93 94
Punto 4
Punto 5
Cálculo de los intervalos:
Rango=Máximo-Mínimo=94-2=92
Por ejemplo aproximamos a 100 y hacemos
intervalos de amplitud 20

11. TEMA 3
Distribución de frecuencias
Punto 1 Ejemplo: distribución de frecuencias agrupadas
Punto 2 DATOS:
Punto 3
2 4 5 9 10 24 27 39 47 54 55 56 59 60 62 76
Punto 4 77 79 80 85 91 91 92 93 94
Punto 5
Intervalo Marca de Frecuencia Frecuencia
(Ii) clase (ci) absoluta (fi) relativa (Fi)
[0, 20[ 10 5 0.2
[20, 40[ 30 3 0.12
[40, 60[ 50 5 0.2
[60, 80[ 70 5 0.2
[80, 100[ 90 7 0.28
25 1

12. TEMA 3
Distribución de frecuencias
Punto 1 Histograma de frecuencias:
Punto 2
EDAD
Punto 3 50
Punto 4
40
Punto 5
30
20
Frecuencia
10 Desv. típ. = ,74
Media = 12,4
0 N = 51,00
12,0 13,0 14,0 15,0
EDAD

13. TEMA 3
Distribución de frecuencias
Punto 1 Polígono de frecuencias e histogramas:
Punto 2
Punto 3
Punto 4
Punto 5

14. TEMA 3
Distribución de frecuencias
Polígono de frecuencias e histograma:
Punto 1
Punto 2
Punto 3
Frecuencias absolutas
Punto 4
Punto 5
Frecuencias absolutas acumuladas

15. TEMA 3
Distribución de frecuencias
Punto 1 Diagrama de sectores:
Punto 2
Punto 3 X1
M
Punto 4 17
Punto 5
M
33.3 %
V
34 V
66.7 %

16. TEMA 3
Distribución de frecuencias
Punto 1 Diagrama de barras
Punto 2
Punto 3 X1
40
Punto 4
V
Punto 5 30
34
66.7 %
20
10
M
Frecuencia
17
0
33.3 %
M V
X1

17. TEMA 3
Distribución de frecuencias
Punto 1 Diagrama de barras
Punto 2
SEGUNDO ING. TÉC. INFORMÁTICA DE GESTIÓN
Punto 3
100%
90%
Punto 4 80%
70%
Punto 5 60%
50%
40%
30%
20%
10%
0%
AE AC BD I PED SEE TAC POO
% PRESENTADOS 88.70% 36.75% 70.13% 64.80% 77.27% 75.29% 57.45%

18. TEMA 3
Parámetros y estadísticos
Punto 1 Parámetros y estadísticos de
Punto 2 centralización (dan un valor promedio que
representa a la población o muestra)
Punto 3
Parámetros y estadísticos de posición
Punto 4
(valores en el rango muestral o poblacional que caracterizan
Punto 5 la distribución)
Parámetros y estadísticos de dispersión
(grado de dispersión de la distribución alrededor de un
valor)
EJEMPLO ACLARATORIO

19. TEMA 3
Parámetros y estadísticos
Punto 1 Parámetros y estadísticos de centralización: Dan
Punto 2
un valor promedio que representa a la
población o muestra
Punto 3
Punto 4
Media, mediana, moda
Punto 5
EXPLICACIÓN Y EJEMPLO ACLARATORIO

20. TEMA 3
Parámetros y estadísticos
Punto 1 Parámetros y estadísticos de centralización:
Punto 2
Punto 3
MEDIA
Punto 4
Punto 5

21. TEMA 3
Parámetros y estadísticos
Punto 1 Parámetros y estadísticos de centralización:
Punto 2
Punto 3
MEDIANA
Punto 4
Punto 5

22. TEMA 3
Parámetros y estadísticos
Punto 1 Parámetros y estadísticos de centralización
Punto 2
Punto 3
Media: (1+2+4+5+7)/5=3.8
Punto 4 Mediana: 4, elemento de la posición 3
Punto 5
Moda: --
Datos: 1 2 4 5 7

23. TEMA 3
Parámetros y estadísticos
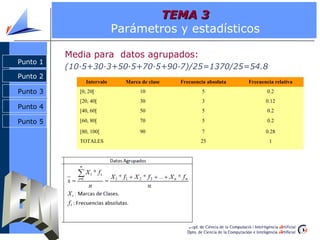
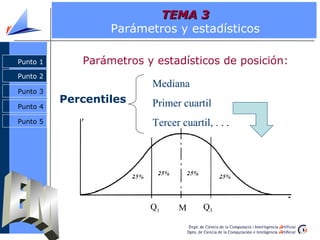
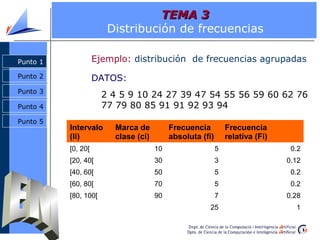
Punto 1 Parámetros y estadísticos de centralización
Punto 2
Punto 3
Mediana: 4, elemento de la posición 3
Punto 4 Si n es impar la mediana es el elemento que
ocupa la posición [n/2]+1
Punto 5
5/2=2.5 [2.5]+1=2+1=3x3=4
Datos: 1 2 4 5 7

24. TEMA 3
Parámetros y estadísticos
Punto 1 Parámetros y estadísticos de centralización
Punto 2
Punto 3
Mediana: 3
Punto 4 Si n es par la mediana es la media de los dos
elementos centrales, es decir, los que ocupan la
Punto 5
posición n/2 y (n/2)+1
4/2=2 (x2+x3)/2=(2+4)/2=3
Datos: 1 2 4 5

25. TEMA 3
Parámetros y estadísticos
Punto 1 Parámetros y estadísticos de centralización
Punto 2
Punto 3
Media: (1+2+4+5)/4=3
Punto 4 Mediana: 3, media entre los elementos
Punto 5 de la posición 2 y 3
Moda: --
Datos: 1 2 4 5
Datos: 1 2 2 2 4 5
Moda: 2

26. TEMA 3
Parámetros y estadísticos
Punto 1 ¿Media o Mediana?
Punto 2
En general la media es una excelente medida de
Punto 3 centralización pero a veces la mediana es más útil
Punto 4 • Es más robusta ante la presencia de anomalías
Punto 5
2, 5, 6, 7, 9media:5.6, mediana: 6
2, 5, 6, 7, 99media:23.8, mediana: 6

27. TEMA 3
Parámetros y estadísticos
Punto 1
¿Media o Mediana?
Punto 2
Deja un 50% de observaciones por encima y 50 por
Punto 3 debajo y esto da unas ventajas que no tiene la
media.
Punto 4
• Nota en un examen
Punto 5 – Si la mediana es 5, seguro que el 50% han
aprobado
– Si la media es 5 no sabemos cuántos han
aprobado:
» 41 han sacado un 4
» 8 han sacado un 10
» 1 ha sacado un 6

28. TEMA 3
Parámetros y estadísticos
Media para datos agrupados:
Punto 1
(10·5+30·3+50·5+70·5+90·7)/25=1370/25=54.8
Punto 2
Intervalo Marca de clase Frecuencia absoluta Frecuencia relativa
Punto 3 [0, 20[ 10 5 0.2
[20, 40[ 30 3 0.12
Punto 4
[40, 60[ 50 5 0.2
Punto 5 [60, 80[ 70 5 0.2
[80, 100[ 90 7 0.28
TOTALES 25 1

29. TEMA 3
Parámetros y estadísticos
Punto 1 Parámetros y estadísticos de posición:
Punto 2
Mediana: q(0.5) o Q2 o M o Me
Punto 3
Percentiles
Punto 4 Primer cuartil: q(0.25) o Q1
Punto 5
Tercer cuartil: q(0.75) o Q3
El percentil p, 0<p<1, que denotamos por q(p) (o P 100p) es el
valor de la curva de frecuencias que deja a su izquierda el
100p% de la masa

30. TEMA 3
Parámetros y estadísticos
Punto 1 Parámetros y estadísticos de posición:
Punto 2
Mediana
Punto 3
Percentiles Primer cuartil
Punto 4
Punto 5 Tercer cuartil, . . .
Q1 M Q3

31. TEMA 3
Parámetros y estadísticos
Parámetros y estadísticos de posición (SPSS)
Punto 1
Punto 2 DATOS:1.23, 1.47, 2.25, 3.47, 5.43, 6.54, 7.28, 8.56
Punto 3
Posición del primer cuartil=(n+1)/4
Punto 4
•Si este valor es entero se busca el dato que ocupa ese lugar
Punto 5
•Si ese valor es decimal se usa la fórmula: v i(1-α)+vjα, donde
α es la parte fraccionaria de la posición y v i, vj los valores que
ocupan las posiciones más cercanas por defecto y por exceso
a la posición del cuartil, respectivamente
(8+1)/4=2.25 α=0.25
Q1=x2(1-0.25)+x3(0.25)=1.47(0.75)+2.25(0.25)=1.1025+0.5625
Primer cuartil: 1.665

32. TEMA 3
Parámetros y estadísticos
Parámetros y estadísticos de posición (SPSS)
Punto 1
Punto 2 DATOS:1.23, 1.47, 2.25, 3.47, 5.43, 6.54, 7.28, 8.56
Punto 3
Posición del tercer cuartil=3(n+1)/4
Punto 4
•Si este valor es entero se busca el dato que ocupa ese lugar
Punto 5
•Si ese valor es decimal se usa la fórmula: v i(1-α)+vjα, donde
α es la parte fraccionaria de la posición y v i, vj los valores que
ocupan las posiciones más cercanas por defecto y por exceso
a la posición del cuartil, respectivamente
3(8+1)/4=6.75 α=0.75
Q3=x6(1-0.75)+x7(0.75)=6.54(0.25)+7.28(0.75)=1.635+5.46
Tercer cuartil: 7.095

33. TEMA 3
Parámetros y estadísticos
Parámetros y estadísticos de posición (SPSS)
Punto 1
Punto 2
Posición del primer cuartil=(n+1)/4
Punto 3
Posición del tercer cuartil=3(n+1)/4
Punto 4 Posición de la mediana=(n+1)/2
Punto 5  Posición del percentil q=q(n+1)

34. TEMA 3
Parámetros y estadísticos
Punto 1 Parámetros y estadísticos de
Punto 2 dispersión:
Punto 3 Varianza
Punto 4 Desviación típica
Punto 5
Coeficiente de variación de Pearson
Recorrido intercuartílico
EJEMPLO ACLARATORIO

35. TEMA 3
Parámetros y estadísticos
Punto 1 Parámetros y estadísticos de dispersión:
Punto 2
Varianza y desviación típica
Punto 3
Punto 4
Punto 5

36. TEMA 3
Parámetros y estadísticos
Punto 1 Parámetros y estadísticos de dispersión:
Punto 2
Coeficiente de variación de Pearson:
Punto 3
CV=Desviación típica/Media
Punto 4
Recorrido intercuartílico:
Punto 5
RIQ=Q3-Q1 (también denotado por IQR, siglas inglés)

37. TEMA 3
Parámetros y estadísticos
Punto 1
Parámetros y estadísticos de dispersión
Punto 2
Punto 3
N Mínimo Máximo Media Desv. Varianza
Punto 4 típ.
HORASDEP 51 2,0 15,0 5,363 3,4279 11,751
Punto 5 N válido (según 51
lista)
CV=S/Media=3.4279/5.363=0.639

38. TEMA 3
Forma
Punto 1 Forma:
Punto 2
Simétrica (media=mediana)
Punto 3
Asimétrica a la derecha (media > mediana)
Punto 4
Asimétrica a la izquierda (media < mediana)
Punto 5
HORASDEP:
media: 5.363
mediana: 5
EJEMPLO ACLARATORIO

39. TEMA 3
Forma
Punto 1
Histograma
Punto 2
Punto 3 25 HORASDEP:
Punto 4
media: 5.363
20
mediana: 5
Punto 5
Frecuencia
15
10
5
Mean = 5,363
Std. Dev. = 3,4279
0 N = 51
2,0 4,0 6,0 8,0 10,0 12,0 14,0 16,0
horasdep

40. TEMA 3
Gráficos caja
Punto 1 Ejemplo: Obtén un diagrama de tallos y hojas de estos datos:
Punto 2 68 82 70 79 101 83 95 70 88 69 78 85 92 73 82 70 84 68 82 74
Punto 3
Punto 4
6 889
Punto 5
7 0003489
8 2223458
9 25
10 1

41. TEMA 3
Gráficos caja
Punto 1 Ejemplo: Atendiendo a los siguientes datos que corresponden con
Punto 2 las edades de 50 personas, obtén el gráfico caja
Punto 3
Punto 4
Punto 5

42. TEMA 3
Gráficos caja
50 1.5*(RIQ)
1.5*(RIQ)
Punto 1
Punto 2
1.5
18
Punto 3
v.a 17 20
Punto 4 18 19
Punto 5
f 16.5 20.5
Mediana: 18
Q1=18 ninguno tres 21, 21, 21
F
Q3=19 15 22
RIQ=Q3-Q1=19-18=1 ninguno uno 24

43. TEMA 3
Gráficos caja
Punto 1
Punto 2
Punto 3
Punto 4
Punto 5

44. TEMA 3
Gráficos caja
Punto 1 Ejercicio: Consideremos los siguientes datos:
Punto 2 68 82 70 79 101 83 95 70 88 69 78 85 92 73 82 70 84 68 82 74
Punto 3
• Calcula la mediana, Q1 y Q3 según SPSS
Punto 4
• Obtén los gráficos de apoyo para obtener el gráfico caja
Punto 5
• Obtén el gráfico caja

45. TEMA 3
Gráficos caja
Punto 1 Ejercicio: 68 82 70 79 101 83 95 70 88 69 78 85 92 73 82 70 84
Punto 2 68 82 74
Punto 3
Punto 4
6 889
20
Punto 5
7 0003489
80.5
8 2223458
9 25
70 84.75
10 1

46. TEMA 3
Gráficos caja
Punto 1 Ejercicio (continuación):
Punto 2 20
Punto 3
80.5 22.125
Punto 4
Punto 5
70 84.75 68 101
6 889 47.875 106.875
7 0003489 -- --
8 2223458 25.75 129
9 25 -- --
10 1

47. TEMA 3
Gráficos caja
Punto 1 Ejercicio (continuación):
Punto 2
Punto 3 100,00
Punto 4
Punto 5
90,00
80,00
70,00
VAR00001

48. TEMA 3
Práctica
Punto 1
Punto 2
Punto 3
Punto 4
Punto 5
PARA HACER EN LABORATORIO